單星測頻靜態(tài)目標無源定位研究

北京遙感信息研究所，北京 100192

隨著通信電子技術(shù)的迅速發(fā)展，探測定位技術(shù)的應用越來越廣泛，特別是在軍事斗爭中的地位和作用不斷提高。在越來越強調(diào)隱蔽攻擊的趨勢下，傳統(tǒng)的有源探測定位技術(shù)暴露出隱蔽性差、截獲率高的弱點。因此，采用被動方式工作的無源探測定位技術(shù)越來越受到重視，正逐漸成為定位方法發(fā)展的主流[1-5]。它比有源探測定位方法具有作用距離遠、寬帶工作、低截獲概率等優(yōu)點，是現(xiàn)代電子對抗中不可缺少的重要手段，同時在航海、航空、宇航、偵察、測控、救援和地球物理學中也扮演著重要的角色。

在星載無源定位系統(tǒng)中，常采用干涉儀測向或時差方法對地面輻射源進行定位。干涉儀測向定位利用一顆衛(wèi)星即可實現(xiàn)對地面干擾源進行定位，算法簡單，但是天線結(jié)構(gòu)復雜，需要解相位模糊，測向通道的相位一致性要求也較高，并且由于受測向精度的限制，定位誤差一般為幾十千米。時差定位需要多顆衛(wèi)星才能進行定位，技術(shù)比較復雜，成本較高，對衛(wèi)星星座時統(tǒng)的一致性要求非常高，在工程應用中實現(xiàn)難度較大[6-8]。

單星測頻定位技術(shù)利用觀測平臺和目標之間相對運動所產(chǎn)生的多普勒頻率對輻射源進行定位。對于地面輻射源，一顆衛(wèi)星通過對同一地面目標進行4次測量就可確定輻射源的位置。由于低軌衛(wèi)星的移動速度很快，產(chǎn)生的多普勒頻率大，因而有利于定位精度的提高，而且單顆衛(wèi)星降低了系統(tǒng)實現(xiàn)難度和發(fā)射成本，還可以通過多次測量來提高定位精度[9-10]。

本文首先分析了單星測頻定位技術(shù)的基本原理，提出了基于非線性最優(yōu)化技術(shù)的求解算法。然后，結(jié)合工程實際，探討了數(shù)據(jù)測量、數(shù)據(jù)預處理技術(shù)和系統(tǒng)誤差分離技術(shù)。最后通過一組仿真試驗和多次實際應用驗證了單星測頻定位技術(shù)有效性。

1 單星測頻無源定位方法

根據(jù)運動學原理，當偵察衛(wèi)星與目標輻射源作相對運動時，這種相對運動可以分解為徑向和切向兩個分量，其中，徑向運動分量將導致信號的瞬時頻率存在多普勒頻移現(xiàn)象，而多普勒頻移又表征為衛(wèi)星狀態(tài)信息和輻射源目標位置參數(shù)的非線性函數(shù)[11-12]。因此，可以基于最優(yōu)化技術(shù)求解非線性模型，從而實現(xiàn)對輻射源目標的定位與跟蹤，如圖1所示。

圖1 星載測頻定位原理Fig.1 Schematic diagram of passive localization of single satellite using frequency measurement

1.1 頻率測量定位建模與最優(yōu)化求解技術(shù)

假設偵察目標在地心固連坐標系中的位置可以表示為：

(1)

在衛(wèi)星觀測時間內(nèi)，可以將目標的位置表示為一個3次多項式，即：

(2)

(3)

(4)

對于固定目標，在式(2)～(4)中，只取常數(shù)項，對于勻速運動目標，只取常數(shù)項和一次項，而對于勻加速運動目標只取常數(shù)項、一次項和二次項。

因此，目標和衛(wèi)星之間的相對距離及其導數(shù)為

(5)

(6)

(7)

(8)

(9)

其中，衛(wèi)星的位置和速度信息由GPS數(shù)據(jù)提供。

根據(jù)多普勒原理可知，偵收信號頻率可表示如下：

(10)

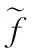
(11)

式(11)中的未知數(shù)只有目標的位置和速度信息。因此，可以基于梯度下降法最優(yōu)化搜索策略，由式(11)可實現(xiàn)對目標的定位，構(gòu)造如下最優(yōu)化模型：

(12)

為了求解最優(yōu)化模型(12)，還需要確定搜索區(qū)域。對于測向定位體制，由于已經(jīng)獲得了初始定位點，因此，其搜索區(qū)域可以設為初始定位點附近。但是，如果沒有初始定位點信息，則由于多普勒頻移只與目標和衛(wèi)星之間相對距離的變化率有關(guān)。因此，最優(yōu)化模型(12)必然存在兩種關(guān)于衛(wèi)星軌道對稱分布的最優(yōu)結(jié)果，在沒有其他信息的前提下，需要人工判定，舍棄其中的一個模糊點，保留真實的定位點。

為了提高最優(yōu)化模型(12)估計精度和穩(wěn)定性，還需要做一些相關(guān)處理工作。首先，由于式(2)～(4)中位置參數(shù)過多，會影響后續(xù)最優(yōu)化求解，因此，為保證估計精度，需要進行降維處理。由于一般低速運動目標相對于衛(wèi)星運動速度是可以忽略不計的，因此，可以基于固定目標情形來討論。由于大地坐標系與地心固連坐標系的坐標轉(zhuǎn)換為：

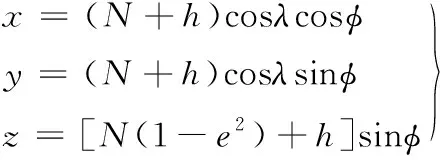
(13)

1.2 頻率測量數(shù)據(jù)預處理技術(shù)

(1)野值點剔除

在衛(wèi)星測量數(shù)據(jù)中，由于信噪比較低，會產(chǎn)生大量的野值點。這些野值點的特性不同于隨機噪聲，其幅度是遠大于隨機噪聲的，而且分布不均勻，無規(guī)律，如果不將其剔除，會嚴重影響數(shù)據(jù)處理過程和定位精度。

對于野值點地剔除，已有大量文獻對其進行了研究[5]，并提出了許多相關(guān)技術(shù)手段和方法。幾乎所有野值剔除方法都利用了野值點的一個重要特征，即野值點的跳躍性。一般情況下，野值點幾乎無連續(xù)性和光滑性可言。因此，本平臺也是以此特征作為突破口，采用函數(shù)逼近理論，剔除野值點，提取真實弱信號。

設測量數(shù)據(jù)為y(t)，真實值為x(t)，隨機誤差為ξ(t)，野值點為δ(t)，則有:

y(t)=x(t)+δ(t)+ξ(t)

(14)

將真實信號x(t)表征為一組正交基函數(shù)的線性組合，即

(15)

將式(15)代入式(14)，則有

y(t)=H(t)·c+δ(t)+ξ(t)

(16)

圖2 單星測頻定位流程Fig.2 Flowchart of passive localization method of single satellite using frequency measurement

為了有效剔除野值點，首先需要正確識別野值點。若記E(t)=y(t)-H(t)·c，如果t時刻存在野值點，則E(t)將具有較大的方差，即

(17)

因此，可以基于式(17)識別t時刻是否存在野值點。

在實際應用中，可以事先設定一個閾值γ，則可以構(gòu)造如下判斷準則，判斷t時刻是否存在野值點：

(18)

一般情況下，閾值γ≤3，即通常的3σ原則。

在式(18)中需要已知事先模型參數(shù)c和噪聲方差σζ，而為了求得模型參數(shù)c，則必須首先識別出真實信號x(t)。由于野值點具有無規(guī)律的大幅度跳躍這一特性，而真實信號則是一個緩變的光滑信號，因此，可以基于測量信息y(t)的導數(shù)信息進行判斷。

若令二階差分：

Δy(t)=[y(t+Δt)-2y(t)+y(t-Δt)]/2Δt

式中：Δt為采樣間隔。構(gòu)造如下判斷準則，判斷t時刻是否真實信號：

(19)

式中：閾值ρ≤1。

由式(19)識別出真實信號后，若記存在信號的時刻為tI，則可得：

(20)

式中：HI=H(tI)，yI=y(tI)。

將式(20)代入式(15)，則有:

x(tI)=H(tI)·cI

(21)

從而可得:

E(tI)=y(tI)-x(tI)

(22)

由式(22)即可估計噪聲方差σζ。

因此，基于式(18)～(22)可以有效剔除野值點和提取弱信號，試驗中野值剔除前與剔除后對比如圖3、圖4所示。此外，如果經(jīng)過上述處理流程，一次未能完全把野值點剔除干凈，則可以將第一次處理后的測量信息作為新的測量信息，再按上述流程進行處理。經(jīng)過這樣幾次循環(huán)迭代后，可以將野值點完全剔除干凈。

圖3 野值點剔除前的頻率Fig.3 Frequency distribution without outlier elimination

圖4 野值點剔除后的頻率Fig.4 Frequency distribution after outlier elimination

(2)隨機誤差平滑

在數(shù)據(jù)處理中，經(jīng)常會碰到測量數(shù)據(jù)中的隨機誤差，這些隨機誤差在一定程度上會影響數(shù)據(jù)處理結(jié)果和精度，需要對其加以抑制和平滑。在目標定位與跟蹤領(lǐng)域，較為傳統(tǒng)的隨機誤差平滑技術(shù)是非線性濾波技術(shù)，比如擴展卡爾曼濾波、不敏卡爾曼濾波、粒子濾波和偽線性濾波技術(shù)等方法。這些濾波方法具有很好的時效性，但是，在迭代過程中，所有這些濾波方法[5]均只利用了當前時刻以前的測量信息，而當前時刻以后的信息則不參與運算，使得迭代過程有可能會發(fā)散和失真。

對于衛(wèi)星輻射源定位領(lǐng)域，由于一般采用事后處理，而且在單星情況下是很難保證定位的實時性。因此，本平臺采用函數(shù)逼近理論對隨機誤差進行平滑，這種方法可以有效地將全程數(shù)據(jù)進行融合處理，最大限度地利用測量信息。

假設測量數(shù)據(jù)為y(t)，真實值為x(t)，測量隨機誤差為ξ(t)，則有：

y(t)=x(t)+ξ(t)

(23)

假設x(t)為一連續(xù)函數(shù)，則根據(jù)函數(shù)逼近理論，可以將x(t)表示為一組正交基函數(shù)的線性組合，即:

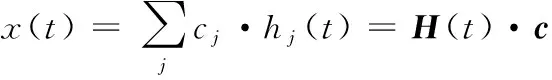
(24)

式中：hj(t)為一組正交基函數(shù)，一般可以選擇多項式基、三角函數(shù)基和B-樣條函數(shù)基等。將式(24)代入式(23)，則有:

y(t)=H(t)·c+ξ(t)

(25)

因此，為了平滑隨機噪聲ξ，提取信號x(t)，則只須求解式(25)中的模型參數(shù)c。若假設噪聲ξ(t)是線性無關(guān)的，則根據(jù)最小二乘技術(shù)可得

c=(HT·H)-1·H·y

(26)

式中：y=y(t)；H=H(t)。將式(26)代入式(25)，則有

x(t)=H·(HT·H)-1·H·y

(27)

通過式(27)即可實現(xiàn)對隨機誤差的抑制和平滑，同時也可以有效的從測量信息y(t)提取真實信號x(t)。由于該方法利用了所有觀測時刻的測量信息，使得信號估計結(jié)果能很好的與真實值吻合，而且可以通過調(diào)節(jié)基函數(shù)類型和參數(shù)，可以獲得更優(yōu)的估計結(jié)果，試驗中原始數(shù)據(jù)經(jīng)隨機誤差平滑處理后的效果如圖5所示。

圖5 平滑后的頻率Fig.5 Frequency distribution after stochastic error processing

(3)頻率測量數(shù)據(jù)系統(tǒng)誤差建模與分離技術(shù)

由于受復雜電磁環(huán)境和接收機性能影響，星載頻率測量值可用下式表征：

(28)

一般情況下，系統(tǒng)誤差是一個隨時間緩變的小量，可以用多項式函數(shù)來表征，即：

(29)

式中：gj(t)為多項式基函數(shù)；d為模型參數(shù)。

通過對實際偵收數(shù)據(jù)的分析，不同時刻的隨機誤差之間存在一定的相關(guān)性。根據(jù)時間序列分析方法，可以用自回歸序列AR模型來表征隨機噪聲，即：

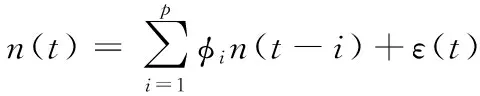
(30)

式中：p為模型階數(shù)；φi為自回歸系數(shù)；ε(t)為零均值高斯白噪聲，且n(t)與ε(t)不相關(guān)。

引入后移算子B，即B·n(t)=n(t-1)，則可將式(30)簡化為：

Φ(B)·n(t)=ε(t)

(31)

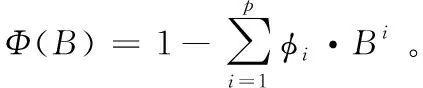
由式(28)～(31)可知，測量噪聲

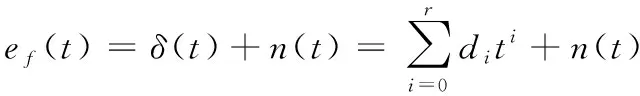
(32)

式中：n(t)為零均值平穩(wěn)AR(p)序列；P為自回歸序列AR模型階數(shù)；r為多項式函數(shù)階數(shù)。式(32)中所稱為PAR模型(P為Polynomial的縮寫)[4]。

將式(31)代入式(32)，可得：

(33)

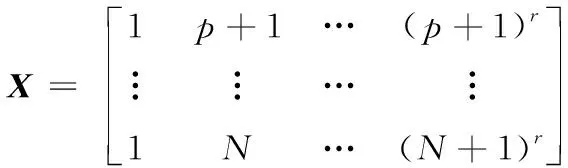
(34)

a=(XT·X)-1·XT·(Y-M·φ)

(35)

RSS=(Y-M·φ)T·(I-H)·(Y-M·φ)

(36)

式中：投影矩陣H=X·(XT·X)-1·XT，I為單位陣。由于式(36)是關(guān)于φ的二次函數(shù)，則φ可由下式求得：

φ=[MT·(I-H)·M]-1·MT·(I-H)·Y

(37)

由式(37)求得自回歸系數(shù)φ后，將其代入式(36)，即可得到零均值高斯白噪聲ε(t)的方差估計值

(38)

關(guān)于AR模型階數(shù)和多項式階數(shù)的確定，可以采用AIC準則，即：

(39)

在實際應用中 ，一般取多項式階數(shù)不超過3階，自回歸系數(shù)不超過30階。

2 試驗結(jié)果分析

為了保證定位結(jié)果的可靠性和準確性，一般要求信號中心頻率恒定，接收信號的頻率測量精度小于100 Hz，信號持續(xù)時間大于30 s。圖6顯示了測頻定位誤差與測頻的關(guān)系，其中，信號接收時間為30 s，采樣間隔為20 ms，輻射源頻率為1 500 MHz，蒙特卡洛仿真次數(shù)為100次。

圖6 測頻定位誤差與測頻精度的關(guān)系Fig.6 Relation between positioning error and frequency measurement precision

在實際仿真試驗中，計算結(jié)果為(東經(jīng)122.948 7°，北緯30.918 8°)與(東經(jīng)131.618 4°，北緯32.635 3°)，根據(jù)測向結(jié)果的輔助人工判證，定位結(jié)果應為(東經(jīng)122.948 7°，北緯30.918 8°)。在實際試驗過程中，分別對多個固定通信輻射源進行了定位，定位精度較以往提高了10 km。此外，還對手持終端進行了定位測試試驗，采用普通對講機，信號為FM話音調(diào)制信號，試驗結(jié)果表明，定位誤差(CEP)也得到了大幅度提高。

3 結(jié)束語

本文提出了利用單顆衛(wèi)星單個通道在不同位置上測量信號的多普勒頻率實現(xiàn)對地面固定輻射源的無源定位方法，該方法具有有效載荷簡單、對衛(wèi)星姿態(tài)無特殊要求、定位收斂快、精度較高等優(yōu)點。同時，探討了多普勒頻率測量誤差預處理技術(shù)，以及基于PAR模型的系統(tǒng)誤差分離技術(shù)。通過對測量誤差的分離與處理，可以大幅度提高頻率測量數(shù)據(jù)的精度，從而保證后續(xù)測頻定位精度。最后，通過仿真試驗和工程實際，驗證了單星測頻定位技術(shù)的有效性和準確性。