現代有軌電車嵌入式軌道結構力學性能分析

馮青松 謝發明 孫 魁 劉慶杰

(1.華東交通大學鐵路環境振動與噪聲教育部工程研究中心，330013,南昌；2.蘇交科集團股份有限公司，210019，南京//第一作者，碩士研究生)

現代有軌電車嵌入式軌道結構主要由槽型鋼軌、填充材料、PVC(聚氯乙烯)管、彈性墊板及軌道板等結構組成[1-3]。其中，常用的填充材料為聚氨酯，是一種高度非彈性的高分子材料[4]。為了研究嵌入式軌道力學性能，需建立一種能體現填充材料力學特性的本構模型。

目前，基于填充材料線性本構模型對現代有軌電車軌道結構靜力學和動力學特性等方面的相關研究有很多。文獻[5-8]在對承軌槽內填充材料進行參數分析時，均將彈性體視為線性體，未能充分考慮改性聚氨酯填充材料的非線性對軌道結構力學特性的影響。國內外對承軌槽內填充材料按非線性考慮的研究還比較少。為此，本文建立填充材料的非線性模型及線性模型，分析不同模型對軌道力學性能的影響。

1 計算模型及參數

本文采用ABAQUS有限元軟件來分析嵌入式軌道結構的非線性力學性能。所研究的軌道結構主要由60R2槽型軌、填充材料聚氨酯、PVC管及軌道板等組成。

1.1 填充材料的本構模型

硬度不同的聚氨酯彈性體，其彈性模量取值不同。本文取硬度分別為70～72 A和43 A的兩種聚氨酯材料作為試樣，進行單軸壓縮試驗。相關試驗數據如表1所示。

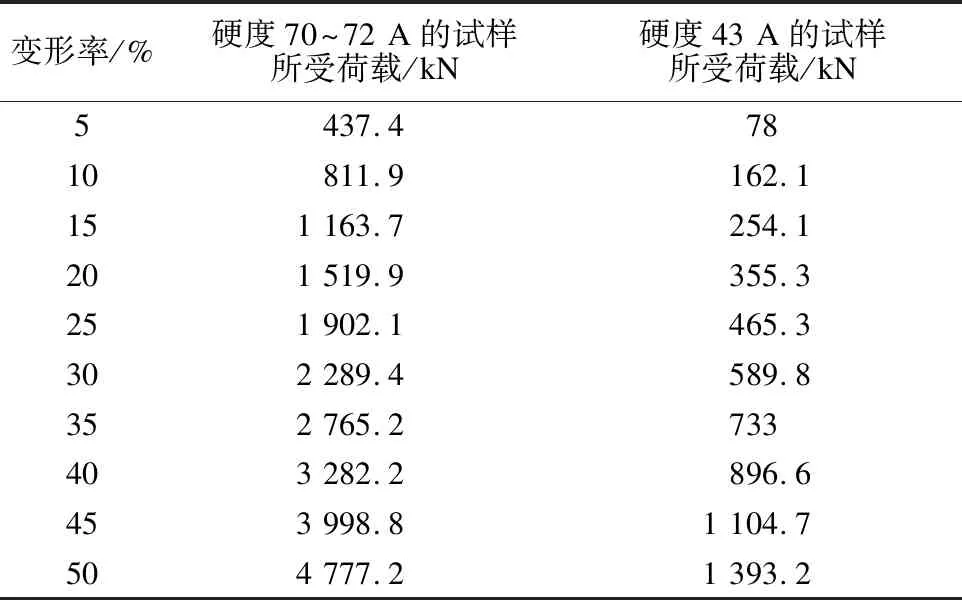
表1 聚氨酯試樣單軸壓縮試驗結果

聚氨酯非線性彈性體需通過應變能密度函數來描述其材料的非線性彈性特征。構建超彈性材料本構模型可使用基于統計理論的本構模型和基于唯象理論的本構模型。基于已有的聚氨酯單軸壓縮試驗數據，使用唯象理論來描述超彈性材料性質是最簡單的途徑。在擬合填充材料本構模型時，應變能函數采用Polynomial和Ogden本構模型。其中，Polynomial多項式的應變能函數表達式為：

式中：

W——應變能函數;

N——多項式階數；

i、j——Polynomial多項式參數；

Cij——同溫度有關的材料參數Rivlin因數；

Di——彈性體的介電常數；

R——彈性體穩定性系數；

I1c——第一偏應變不變量；

I2c——第二偏應變不變量；

Jc——變形后與變形前的體積比，Jc=λxλyλz，其中λx、λy和λz分別為為主伸張率，下標x、y和z分別表示3個相互正交的方向。

Ogden應變能函數的表達式為：

式中:

αi——彈性體材料的應變硬化指數，通過試驗確定；

υi——彈性體材料的剪切模量。

αi、υi、Di和R是與溫度有關的材料參數。它們的數值由聚氨酯材料的單軸壓縮數據確定。其中，冪指數αi能擬合完全非線性試驗數據的任意實數[9-10]。

根據聚氨酯彈性體應力應變性能試驗數據，利用ABAQUS軟件中的材料模塊功能，可獲得適合嵌入式軌道填充材料非線性本構關系。兩種聚氨酯彈性體的非線性本構模型可分別用多項式函數(N=2)和Ogden函數(N=5)來擬合，相應的應變能擬合曲線如圖1所示。由擬合結果可見，兩種非線性本構模型均具有較好的匹配度和穩定性。

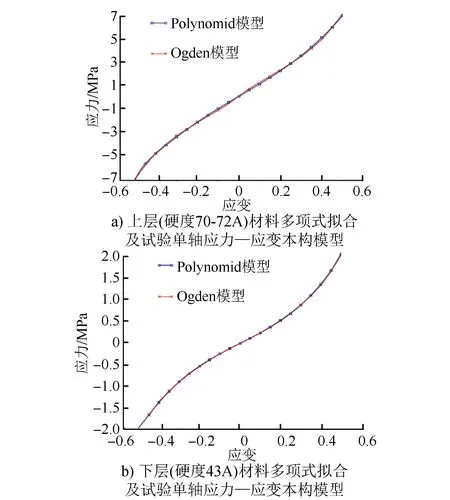
圖1 承軌槽內澆筑的改性聚氨酯填充材料本構模型應變能擬合曲線

1.2 非線性本構模型的正確性驗證

在ABAQUS軟件中建立了與實際試驗試件大小相同的有限元模型，通過試驗數據與仿真結果的對比，來驗證填充材料非線性本構模型的合理性。應力與應變關系的試驗結果及仿真數據如圖2所示。

由圖2可知，兩種聚氨酯材料的仿真應變值與實際試驗應變值最大相差5%。可見，誤差比較小，仿真結果與實際試驗結果近似相等。因此，采用試驗與仿真相結合的方法足以驗證嵌入式軌道填充材料非線性本構模型的正確性。

1.3 計算工況

嵌入式軌道尺寸為5.00 m×1.05 m，軌道板豎直部分高度為180 mm，承軌槽結構平面尺寸為220 mm×200 mm。在ABAQUS有限元軟件中建立三維實體有限元模型，如圖3所示。軌道結構參數如表2所示。

圖3 嵌入式軌道有限元模型

有軌電車實際行駛速度較低，有軌電車最大軸重為12.5 t[11],安全系數取值為1.12。計算模型中，豎向荷載取70 kN,橫向荷載Q=0.6PJ=42 kN。豎向荷載施加于軌頂正中心線上，橫向荷載施加在軌頂面以下14 mm處。在有限元模型中，約束軌道板的兩端及底面，將槽型軌與填充材料的接觸方式設為綁定接觸，將填充材料與混凝土的接觸方式設為為綁定接觸。在進行網格劃分時，槽型軌、軌道板及PVC管網格劃分采用實體單元C3D8R[12]。由于軌底沒有使用彈性墊板，將承軌槽內軌底填充材料按厚度分為20 mm、30 mm和40 mm等3種工況。使用基于填充材料非線性及線性本構模型按工況進行軌道力學性能分析。

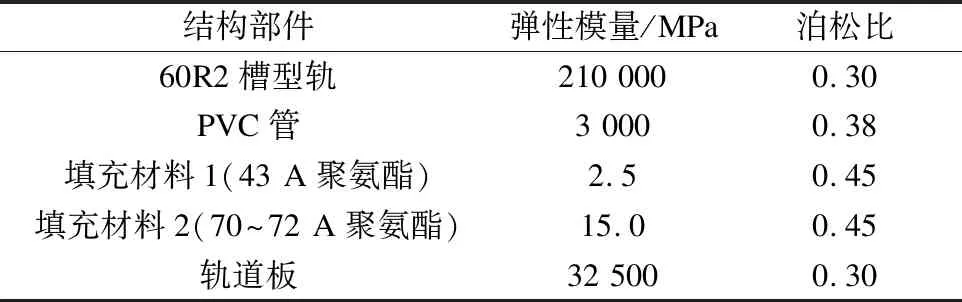
表2 軌道結構參數

在線性本構模型分析中，聚氨酯彈性體的彈性模量按表3取值。

2 非線性模型與線性模型結果對比分析

由計算結果可得，非線性模型與線性模型鋼軌豎向位移計算結果相差不大，填充材料的非線性特征對其位移影響較小。

表3為通過非線性本構模型及線性本構模型，對不同聚氨酯填充材料、不同工況下，軌道結構各部分應力計算的仿真結果。根據表3可得：對填充材料的應力極值，兩種模型的仿真結果相差10%左右；對PVC管應力極值，兩種模型的仿真結果相差8%左右。

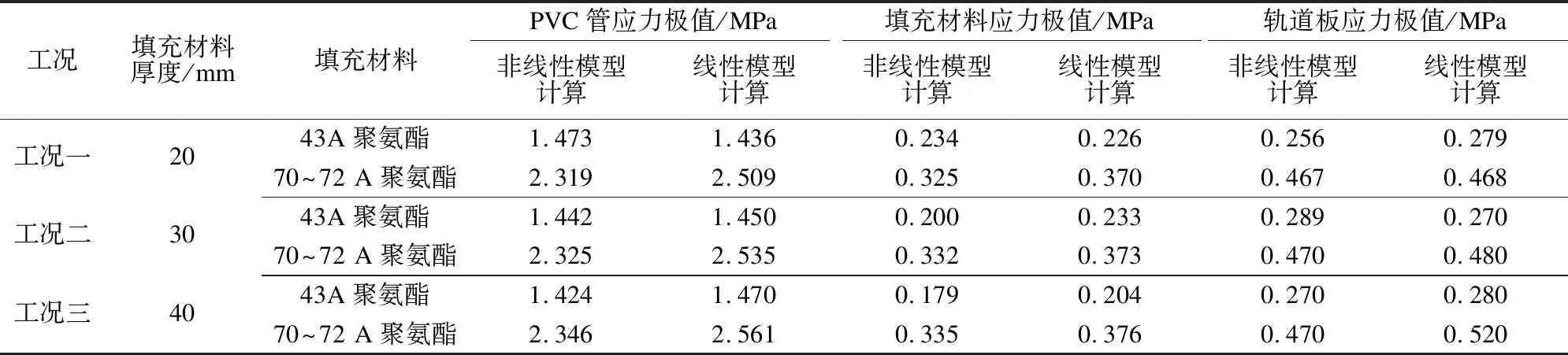
表3 軌道結構各部分應力極值的仿真計算結果

3 不同PVC管直徑對鋼軌位移的影響

3.1 計算模型

本文按5種不同工況,分析PVC管直徑對鋼軌位移的影響。不同工況的模型如圖4所示。

3.2 模型參數

模型長度取5 m，不設置彈性墊板。承軌槽截面尺寸為220 mm×200 mm，軌底填充材料厚度為20 mm。承軌槽結構模型中，60R2槽型軌及PVC管的參數取值見表2，填充材料彈性模量取2～20 MPa、泊松比取0.45。

承軌槽結構底面及兩側施加全約束，網格單元選擇C3D8R。經計算，豎向荷載為70 kN，橫向荷載為42 kN。豎向荷載施加在模型中間鋼軌中心線處，橫向荷載施加在軌頂面以下14 mm處。

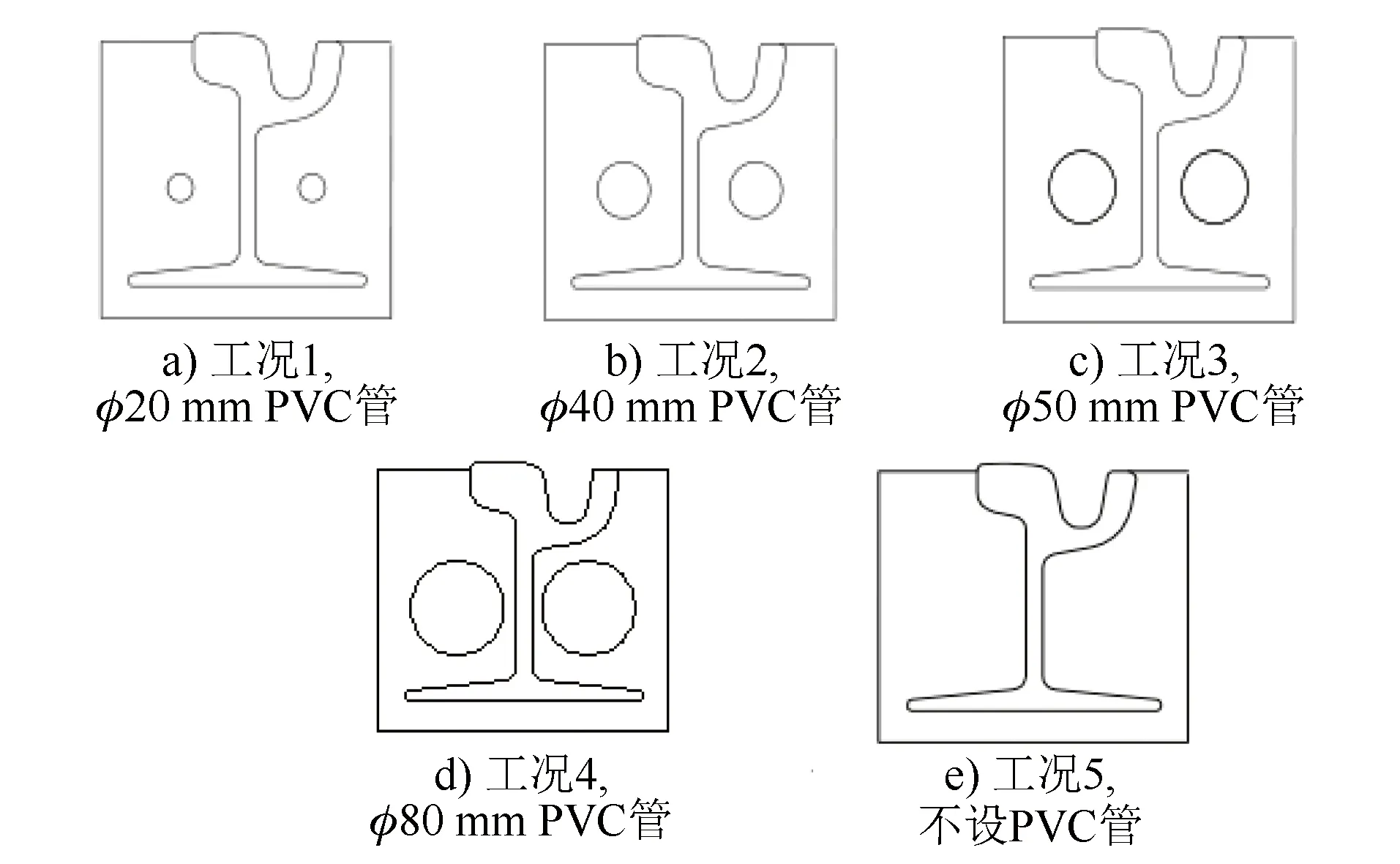
圖4 不同工況的承軌槽計算模型橫斷面示意圖

3.3 承軌槽結構受力分析

圖5～6為不同PVC管的直徑對鋼軌位移值及填充材料應力影響的計算結果。

由圖6可知，改變PVC管的直徑對鋼軌位移模型沒有影響，不同工況的影響曲線基本都是重合。

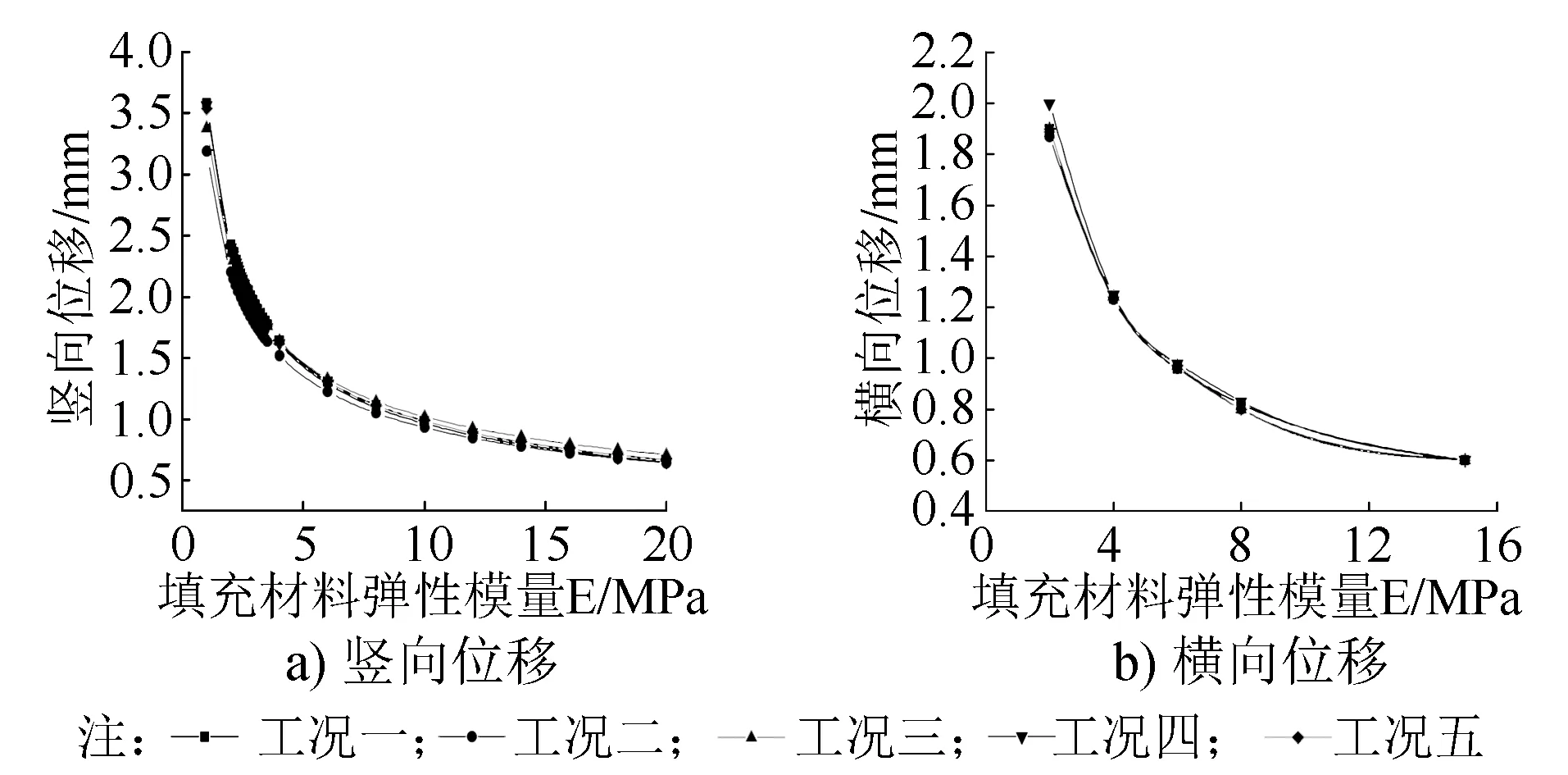
圖5 不同直徑PVC管對鋼軌位移的影響

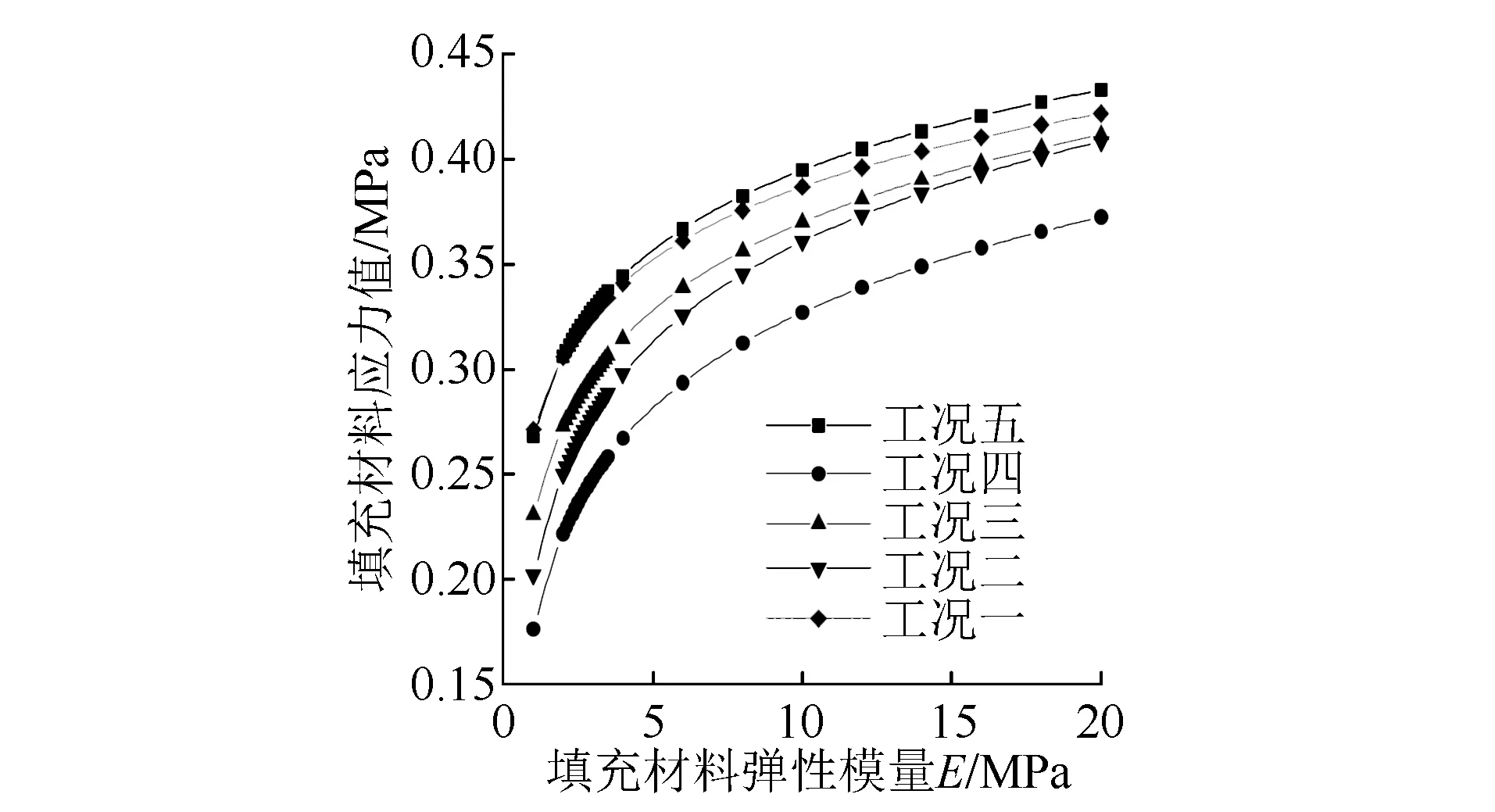
圖6 不同直徑PVC管對填充材料應力的影響

由圖5可知，改變PVC管的直徑，對填充材料的應力會有一定的影響。工況1與工況5填充材料的應力值相同，且隨著填充材料彈性模量的增大，不同工況的曲線基本重合在一起。可見，可以通過設置PVC管來節省填充材料。

4 結論

本文結合填充材料試驗數據，擬合了嵌入式軌道填充材料的非線性本構模型，得到如下主要結論：

1) 采用線性本構模型與非線性本構模型，得到的軌道力學性能分析結果相近。因此，建議在進行嵌入式軌道結構受力分析時，可將聚氨酯材料視為線彈性體，以簡化計算。

2) 嵌入式軌道承軌槽內填充材料的硬度對鋼軌位移有較大影響。相比填充材料彈性模量為2.5 MPa時，當填充材料彈性模量為15 MPa時的鋼軌豎向位移及橫向位移小約為50%。

3) 軌底填充材料厚度對軌道力學性能影響較小。改變槽型軌軌底填充材料厚度，軌道位移及應力變化幅度均小于5%。

4) 在軌底填充材料厚度及開槽寬度相保持不變的情況下， PVC管的直徑對鋼軌位移影響較小。使用PVC管可節省填充材料，減少工程造價。