重視滲透數學文化 培養學生數學素養*
——以知識點“黃金分割”為例
(無錫市第一女子中學,江蘇 無錫 214002)
1 問題提出
《全日制義務教育數學課程標準(2011年版)》和《普通高中數學課程標準(2017年版)》將數學素養作為課程培養目標,國際學生評估項目(簡稱PISA)認為:數學素養是個體在各種情況下形成、使用、詮釋數學的能力.它能幫助作為一個創新、積極和善于反思的公民認識數學在世界中所扮演的角色,并做出良好的判斷和決定[1].然而,許多教師在教學中只重視數學知識的傳授,輕視數學文化的滲透,難道數學知識就是學生數學素養的全部嗎?解題能力是衡量學生數學素養的唯一標準嗎?本文力圖通過初高中銜接知識“黃金分割”,說明數學文化在提高學生數學素養中的重要意義,并給教師教學提出幾點啟示.
2 黃金分割蘊含的數學文化
齊龍新先生認為:數學文化包含知識系統、工具系統、價值系統和史實系統四個層面的內容.其中,知識系統是數學文化的物質基礎,工具系統是數學文化的應用框架,價值系統是數學文化得以發揚的源泉,史實系統是數學文化的歷史積淀,這四大系統構成了數學文化這座大廈[2].黃金分割知識是蘇教版義務教育課程標準實驗教科書《數學》九年級下冊的內容,在考綱中屬于“邊緣考點”.然而,它卻是被德國著名天文學家、物理學家、數學家開普勒稱作的幾何學兩大瑰寶之一,足見其重要地位和價值.
2.1 知識系統
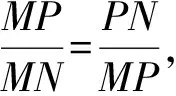
學生進而可求得線段的黃金分割點有兩個,并能計算線段黃金分割點的位置.數學知識的傳授無疑是一種數學文化的傳播,沒有數學的知識體系,也就沒有什么數學文化了.
2.2 工具系統
隨著科技的發展以及數學文明的積累,跨學科交流日趨頻繁,數學的應用更是體現在方方面面.比如涉及對群體的描述,可借助集合語言;研究供求、效益、增長率等經濟學問題,可以借助函數;研究曲面圖形問題,可以利用積分等等.但受限于目前初高中課程內容設置的局限性,無法為學生提供足夠的工具,這是學生感到數學學習無用的重要原因之一.把數學文化滲透到教學中,就是要鮮明突出這種工具性作用.
黃金分割在科學、藝術、建筑、技術等領域有著廣泛的運用,是數學工具性的重要體現.許多氣勢雄偉的建筑蘊含黃金分割,如希臘神殿、多倫多電視塔;名垂千古的雕像中蘊含黃金分割,如米洛斯的“維納斯”“雅典娜女神像”;絢麗奇妙的繪畫中蘊含黃金分割,如達芬奇的“蒙娜麗莎”、拉斐爾的“圣女像”;慷慨激昂的曲譜中蘊含黃金分割,如莫扎特的《D大調奏鳴曲》、貝多芬的《悲愴奏鳴曲》.此外,攝影中的構圖比例、股市行情中的黃金分割線、軍事中的排兵布陣等,都與黃金分割這一古老而神奇的數學瑰寶緊密聯系.教師可通過對所授知識的價值性的滲透,使學生認識到數學對他們將來所從事的行業是有用的,數學是他們未來所從事工作的基礎性工具.
2.3 價值系統
如果說工具系統是數學文化的顯在體現,那么數學的價值系統具有隱性且重要的意義.數學是訓練和培養人思維的重要學科,將潛移默化地影響人們的思考方式和提高人們的認知水平,包括直觀、抽象、建模、類比、推理邏輯、數據處理等,而且還常與高考數學的命題背景或解題結果相關聯.

圖1
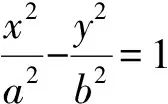
1)雙曲線的離心率e=______;
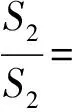
(2012年湖北省數學高考理科試題第14題)
解1)由于以A1,A2為直徑的圓內切于菱形F1B1F2B2,則點O到直線F2B2的距離為a,因此在△F2OB2中,
又c2=a2+b2,聯立可得
(e2-1)2=e2,
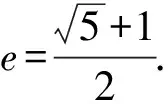
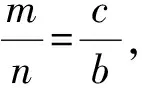
于是
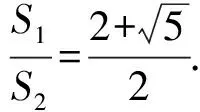
此高考題考查圓錐曲線的性質以及含字母代數式的運算.求出該雙曲線的離心率恰與黃金分割數相關(黃金分割數的倒數,斐波那契數列通項中的重要常數),命題者將黃金分割數蘊藏于出題藝術中,計算出的結果給學生以美的享受.
不僅如此,數學的隱性價值還有助于培養學生用數學眼光觀察世界的能力,用數學的思維方式去處理各種現實問題.
2.4 史實系統
數學史實是體現數學問題與概念、理論與方法來龍去脈的重要依據.教學中數學史的滲透有助于學生建立數學的整體意識,培養學生學習數學的興趣,形成數學家式的思維模式,感知數學家們在探求道路上的不易,從而感悟數學觀念和文化內涵.
古希臘雅典學派數學家歐多克斯首次證明:正五邊形的每兩條對角線被一個交點分成兩段,則整條對角線與較長線段之比等于較長線段與較短線段之比.在柏拉圖學派的歐幾里得編撰的《幾何原本》中也有多處記載有關“黃金分割(數)”的成果.《幾何原本》中許多圖形蘊含豐富的數學語言,若對圖形進行深入挖掘,可推出一系列數學結論,從而更有效地深究一些數學問題的來源.
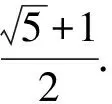
(2010年北京大學、香港大學、北京航空航天大學自主招生題第2題)
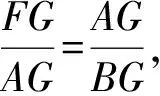
解得
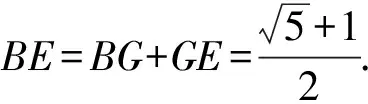
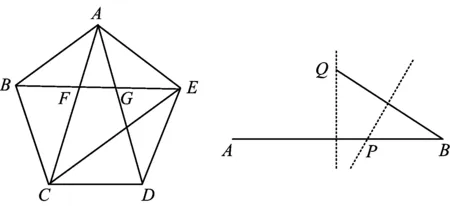
圖2 圖3
點F,G是對角線BE的黃金分割點,同時點F是線段BG的黃金分割點,點G是線段FE的黃金分割點,這種循環還展現了黃金分割的自衍性.
由此,我們還可得到利用尺規和量角器作出線段AB黃金分割點的一種簡易方法(如圖3):在線段AB的中垂線上取點Q使得∠ABQ=36°,作線段BQ的中垂線與線段AB交于點P,則點P是線段AB的一個黃金分割點.
3 數學文化對培養學生數學素養的重要意義
朱德全先生認為:數學核心素養的構成要素具體為數學思維、數學方法、數學思想和數學人文精神[3].數學知識是數學文化的載體,教師通過知識的傳授豐富學生文化的內涵,而適時滲透數學知識的應用價值、探索歷程或數學家們的人文精神對培養學生數學素養起催化作用.
3.1 激發學生學習數學的興趣
按照數學史與數學教育之間的關系(簡稱HPM)的觀點,數學史教育能激發學生學習數學的興趣,更高效實施數學“發生教學”模式,使數學的課堂教學走向學生的深度學習.《幾何原本》《九章算術》等都是重要的數學資料,通過在教學中融入數學文化,學生可以在發展和認知的沖突中親歷數學知識的建構歷程,了解數學科學與人類社會發展之間的相互作用,培養和發展數學家式的思維模式,從而提高自身的數學素養和創新能力.
3.2 提高問題探究的起點
在試題中融入數學史已不少見,此類考題在考查學生思維能力的同時,使學生從歷史角度體會數學文化的價值.熟悉、研究數學史可以高屋建瓴地深究數學問題的題源,從而提高數學探究的起點.
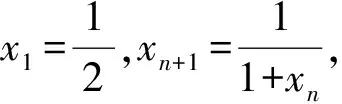
(2009年陜西省數學高考理科試題第22題)
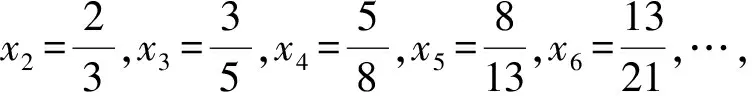
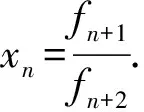
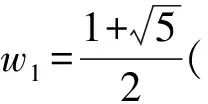
計算得
故x2n+2 數學知識的內化是螺旋式深入的過程,學生數學素養的培養和發展也呈現這一特征.教學中滲透數學文化,有助于學生形成對數學的整體意識,認識數學知識各分支之間的關系,建立起從初中到高中、從高中到大學的數學知識的紐帶,使學生的數學素養得到傳承. 意大利數學史家洛里亞強調:數學史是連接中學數學與大學數學的紐帶.黃金分割或是斐波那契數列在大自然許多場合中都能尋得它們的蹤跡,學生在建立對數學知識整體意識的同時,不斷感受數學的奇妙,這場數學與生活妙不可言的相遇將持續有效地激發他們更加深入地探究數學問題. 站在數學史的高度上深究問題的題源,對提高學生的解題能力大有裨益.問題是數學的核心,數學史上許多著名猜想、公式、定理都是豐富的命題寶庫.將這些問題滲透到數學教學中,通過教師引導下的學生探究,達到“教師答疑解惑的幾分鐘,相當于數學史進展的幾百年”的教學效果.使學生能更好地理解數學,提高數學素養. 學生數學素養的提高是數學文化、數學能力內化的過程,教師的作用更多是啟迪與引領.課堂教學中教師要基于教材知識,有選擇性地指導學生對知識進行發散學習,提煉知識中蘊含的思想方法、來源背景、框架體系等,可以以課后探究的形式讓一部分有能力的學生更多地參與探索,提高他們探究發現的積極性,更加深入全面地開發培養學生的實踐能力和創新意識. 知識需要銜接,文化更要傳承.以題論題的教學方式在很大程度上會增加學生的挫敗感.教師以寬廣的數學文化為底蘊教導學生,不僅能更好地銜接“初中—高中—大學”的數學教育,而且能讓數學更具感染力,在潛移默化中提高學生的數學素養.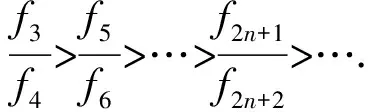
3.3 發展學生數學素養整體性、連續性的紐帶
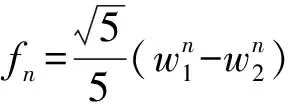
4 給教師教學的幾點啟示
4.1 用數學文化的觀念追究學生疑問
4.2 教師不是數學文化的最大供求者
4.3 提高專業素養,傳承數學文化

