利用白光數字圖像頻域分析法測量動荷載作用下有砟軌道的下沉量

戰啟芳， 杜立峰， 楊新偉， 萬 濤， 程 佳， 王素康

(1. 石家莊鐵路職業技術學院 鐵道工程系 河北 石家莊 050041; 2. 北京交通大學 土木建筑工程學院， 北京 100044)

在高速列車荷載的作用下，鐵路線路的軌道結構會發生不均勻的沉降變形，造成軌道結構幾何形位偏差，會引起整體線路的不平順。在列車動荷載的反復作用下，這種不平順會逐漸加強，最終鐵路軌道的結構功能被破壞。這種軌道結構的破壞就叫做軌道下沉破壞。由于軌道的下沉破壞大都為道床的下沉破壞，所以也被稱為道床下沉破壞。

目前，研究道床下沉的方法有試驗研究和仿真分析這兩種方法。第一種是通過試驗或監測來研究軌道變形，得出軌道變形的經驗公式；第二種方法是以試驗研究為基礎，利用數值仿真來研究軌道的下沉，從理論上為軌道的下沉提供了幫助的參考[1-3]。

20世紀50年代，日本建立了軌道下沉破壞理論[4]，其中為代表的是星野和佐藤(裕)的“最佳軌道結構理論”和以崛越小野的“軌道承載力理論”[5]，最后由佐藤吉彥總結并發展了這些理論，形成了新軌道破壞理論。以此為基礎，后續幾十年里，研究者們進一步地研究和發展軌道下沉破壞理論[6-8]。

而測量軌道下沉的實驗方法主要有以下幾種：

(1) 借助測量道床下沉的測試儀器來測量道床的下沉[9]，主要包括測試儀器、數據采集儀器、各類傳感器。此種測量方法所用儀器較多，所需測量物理量較多，因此測壓力點眾多；將試驗設備安裝在軌道上，當列車通過時，一部分的加速度儀可能會損壞，故不能將此方法用于實際的軌道下沉檢測中。

(2) 基于全站儀和軌檢小車的軌道檢測系統[10]。這種測量方法其移動性不強，設備成本高昂，難以滿足我國當前軌道平順性(包括道床下沉)的巨大檢測數據的需要；用全站儀進行動態位移測量的測量速度遠遠不能滿足結構動態測量的需要。

(3) GPS衛星測量法[11]。具有全天候、自動化、點間無需通視、精度高的特點，但是這一技術對接受天線的環境要求嚴格、測量速率低、成本高且要求高水平專業人員，推廣應用于大型土木結構的可能性較小。

(4) 數字攝影測量法[12]，通過數碼攝像機來獲取圖像，利用計算機處理圖像信息。數字攝影測量可用來檢測軌道幾何平順性，及測量道床的下沉，但數字攝影測量一般是通過專業攝影測量系統，將其用于道床的下沉檢測，不論是其硬件還是軟件系統都有待科研人員做進一步的交叉研究和開發。

由于軌道下沉的相關測量方法精度低、操作復雜、測量成本高。因此，亟待引進一種新的測量方法，能夠克服以上缺點來推動軌道下沉檢測技術的進步。

白光數字圖像頻域分析法[13-14]是一種測量物體位移與變形的數字圖像類的實驗方法。該方法是通過CCD攝像機拍攝被測物體變形前后或運動前后的圖像，將拍攝的圖像輸入計算機，將其數字化，以被測物表面隨機分布的灰度函數為計算對象，將圖像進行傅里葉變換，在頻域中求得位移信息。該方法已經發展了逐點分析法和全場分析法，特別是引入相移法之后，能進行全自動測量。該方法的測試操作系統非常簡單，并且不需要對被測物的表面進行散斑化的特殊處理，對光強的要求也低，且能測量半透明物體的位移與變形。因此，與其他的數字圖像相關法比較，其應用范圍更廣泛。白光數字圖像頻域分析法具有光路簡單，操作方便，能利用CCD攝像機進行近程和遠程測量，測量精度高，能達0.05像素，測量成本低等優點。

本文借鑒文獻[1]對道床結構的研究，利用車輛-軌道耦合動力學理論和道床累積下沉模型，引入白光數字圖像頻域分析法測量軌道的下沉量，并分析不同速度列車對道床下沉變形的影響，并與文獻[1]的研究成果進行對比，得出該方法在測量軌道結構的下沉是否合理。將白光數字圖像頻域分析法引入到有砟軌道下沉量的測試當中，能克服傳統方法的缺點，推動鐵路檢測技術的進步。

1 白光數字圖像頻域分析法原理

對于圖像中的一個微小的區域，可以將該區域內每點的位移看做是相同的。對小區域的圖像直接進行傅里葉變換，可以得到頻譜，將頻譜平方并除以圖像尺寸就得到功率譜。利用一對δ函數來表示同一點變形前后的灰度分布，其中，δ0(x,y)為變形前的灰度函數，δ1(x,y)為相應的變形后的灰度函數，因此有：δ1(x,y)=δ0(x+u，y+v)，見圖1。

該點的位移方向與x軸夾角為θ，位移大小用d來表示，設g為該點變形前后光強之和，即

g(x,y)=δ0(x,y)+δ0(x+dcosθ,y+dsinθ)

( 1 )

對式( 1 )進行一次傅里葉變換，得到其頻譜為

G(X,Y)=G0(Xf,Yf){1+exp[i2π(uX+vY)]}=

2G0(X,Y)[1+exp(-i2πxd)]

( 2 )

式中：

G0(X,Y)=

?δ0(x,y)exp[-i2π(xX+yY)]dxdy=1

(x,y),(X,Y)為該點在物平面和譜平面的坐標；δ0(x,y)和G0(X,Y)分別為該點的散斑圖在變形前的灰度分布及其傅里葉變換；x,d分別為該點在譜平面上的位置矢量和位移矢量。

式( 2 )譜平面上的光強分布可表示為

I=G*G=4cos2[π(r·d)]

( 3 )

從式( 3 )可以得到，當π(r·d)=nπ時，I最大，當π(r·d)=(n-1/2)π時，I最小。即如果以圖像的形式表示，會是一系列平行條紋。

( 4 )

n=0,±1,±2,…

再分析相鄰條紋間距的含義，以N和N′=N+1代表相鄰的條紋級數，在小區域內認為位移是常數，式( 4 )可寫成rN·d=N，rN+1·d=N+1,rN和rN+1是在譜平面的位置，相減可得d=(N+1)-N)/(rN+1-rN)即

( 5 )

式中：d為豎向像素位移值。

利用式(5)可求出位移值，Δr為相鄰條紋間距。

令M為CCD攝像機的成像放大系數，則實際位移D為

( 6 )

根據域變換理論

( 7 )

式中：Lccd為相機的靶面尺寸；ΔK是相鄰條紋間隔的像素值。

聯立式( 7 )和式( 6 )，可得

( 8 )

該方法可以在數秒鐘內在電腦中計算出功率譜，進一步根據條紋間隔大小計算出位移值。

利用白光數字圖像頻域分析法，可以測量出當列車經過時，軌道下沉區域的位移，利用被測區域的位移信息，求出該區域的形變。進一步，根據文獻[1]中的道床累計變形模型，求出道床累計下沉率。

2 實驗裝置和實驗過程

2.1 實驗裝置

一個CCD相機，相機支架，一臺裝有視頻錄制軟件的筆記本電腦。

2.2 實驗過程

以京九線鐵路軌道為實驗對象，實驗地點在河北省石家莊市橋東區太平河段的京九線路。

具體的實驗步驟如下：

Step1將CCD相機安裝在相機支架上，并與計算機相連。

Step2選擇拍攝區域并利用粉筆標記，拍攝區域為鋼軌中間區域，調整相機直到拍攝到清晰的測量區域為止。

Step3利用標尺對測量區域的大小進行標定，拍攝區域大小為73.8 mm×73.8 mm。

Step4進行圖像的拍攝，調整好相機后對列車(軸重為25 t)經過前的鋼軌進行拍攝、記錄，在列車運行時進行拍攝、記錄。

3 實驗數據的處理

列車以160 km/h的速度經過鋼軌前后的圖像見圖2。

3.1 實驗照片的選取

3.2 實驗照片的處理

處理圖片：以整張圖片的中心點為坐標原點(0，0)，在其周圍取點，取步長為1像素，等差取25個點，組成一個五維的矩陣，利用matlab軟件對五維的矩陣進行處理，處理得到一個光滑的三維可視圖形，即為此區域的變形場。取得25個點測點分布見圖3。

利用白光數字圖像頻域分析法可以得到各點的條紋圖見圖4，只顯示部分測點的條紋圖。

3.3 各點像素位移的計算

像素位移為

( 9 )

式中：Δk為條紋的像素位移；Δl為實際量測的兩條紋間距，mm；512為圖片的像素；73.8為照片的實際長度，mm。

(10)

(11)

式中：D為測點的實際豎向位移值，mm。

表1 測量區域各點的實際豎向位移 mm

由計算得出所取各點變形前后的像素位移，用一個的矩陣表示為

再用Matlab軟件將這個五維的矩陣三維可視化，得出整個區域的變形圖像，見圖5。

由圖5、表1可得，變形區域的形變為0.60。

3.4 道床參數的計算

基于文獻[1]的道床下沉累積下沉模型和相關的試驗數據，以及試驗數據得出的結論，可知

(12)

式中：ε為道床應變，10-6ε；σb為道床頂面應力，MPa。

基于文獻[1]給出的道床累積變形模型，可得出道床在穩定階段累積下沉的模型為

(13)

式中：β為道床累積下沉率，mm/次；ab為道床振動加速度；σb為道床頂面應力；c為系數，根據試驗和現場經驗確定，取為4.09×10-7。

參考道床振動加速度方面的研究[1]，總結得出不同速度列車的道床振動加速度，見表2。

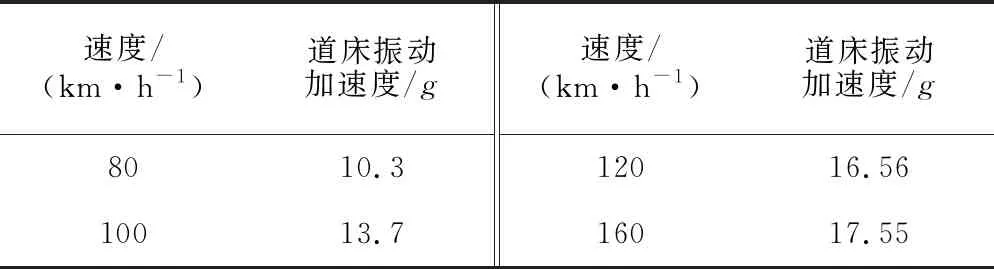
表2 不同速度列車的道床振動加速度

可計算得出，σb=0.055 MPa，β=2.46×10-6mm/次。

3.5 不同速度的列車對道床下沉的影響

通過以京九線石家莊岔河路段的有砟道床為實驗對象，對不同行駛速度的列車對軌道的下沉的影響進行了觀測，測量速度分別為80、100、120、160 km/h四個速度檔，利用相同的方法來研究其他列車對道床沉降造成的影響。處理數據得出結果，提出道床累積沉降率的概念，分析不同速度的列車引起道床的單次下沉量問題。

列車速度分別為80、100、120 km/h時，對應的位移矩陣為A2、A3、A4，測試區域像素位移分布見圖6。

由矩陣數據可得，變形區域的形變為0.524。

由矩陣數據可得，變形區域的形變為0.495。

由矩陣數據可得，變形區域的形變為0.434。

根據變形區域的形變值，可計算出不同列車速度下的道床累計下沉量，見圖7。

由圖7可知，當行車速度由80 km/h分別提高到100、120、160 km/h時，道床累積下沉量分別增大了171%，389%，773%。由圖7可見，隨著行車速度的提高，道床下沉量呈顯著增大趨勢。

在文獻[1]中，作者結合軌道下沉模型和仿真模型，計算出來的單次列車運行下道床的最大下沉量、平均下沉量分別為9.370×10-6、4.669×10-6mm，而此方法計算得出的道床最大下沉量、平均下沉量分別是8.87×10-6、4.67×10-6mm，由于多種因素影響，實際實驗結果和仿真方法分析軌道下沉總存在差異，但是兩者的數量級是一致的，說明本論文的實驗方法分析道床的下沉趨勢是可行的，故可利用數字圖像相關法來測量軌道結構下沉的下沉量。

由圖7可知，在列車動荷載作用下，隨著列車速度的提高，道床的下沉量也相應地提高，但單次荷載作用下道床的下沉量相差不大，可以預測當荷載作用次數超過100 000次后道床的下沉量才比較明顯。根據鐵運〔2006〕146號 《鐵路線路修理規則》[15]中的道床下沉量標準，當道床的下沉量超過4 mm，就必須對道床進行維修。因此利用圖7，可以初步估計不同行車速度和循環次數產生的道床下沉量，為道床的維修提供一定的預測參考。

4 結束語

本文基于車輛-軌道耦合動力學理論和軌道下沉變形法則，利用白光數字圖像頻域分析法測量有砟軌道在列車動荷載作用下的下沉量，并分析不同速度列車對道床下沉變形的影響。利用白光數字圖像頻域分析法測量道床的下沉量與理論計算的道床下沉量相進行比較，相差較小。與文獻[1]的實驗結果做對比，可以看出，本論文所得試驗數據結果同文獻[1]研究所得的結果相差較小，所得實驗結論與文獻[1]所得結論相同。故可利用數字圖像相關法來對軌道的下沉進行觀測。