不確定分數階Genesio混沌系統的反演滑模同步
(河南科技大學 信息工程學院,河南 洛陽 471023)
分數階微積分是研究分數階次的微積分算子特性以及分數階微分方程的理論,已經有逾300年的歷史。隨著對分數階微積分研究的不斷深入,研究者普遍認為分數階微積分是整數階微積分的自然推廣[1],極大地擴展了人們所了解的整數階微積分的描述能力。現今,混沌現象不僅是物理界研究的熱點,也受到了工程技術界的廣泛關注。近年來,混沌系統的控制與同步已成為控制理論與控制工程領域的重要研究內容。
自1990年Pecora和Carroll提出混沌同步的思想以來,混沌系統的同步問題研究得到了蓬勃的發展[2-5],隨著分數階微積分的發展以及混沌系統研究的深入,分數階混沌系統同步及其應用已經成為非線性科學中的一個重要研究課題[6-14],提出了很多分數階混沌系統的同步方法,如模糊控制[9]、變結構控制[10]、非線性控制[11]、自適應控制[12]、耗散控制和反演控制[13]等等。其中反演方法是最常用的方法之一。該方法在遞推過程中,巧妙的構建李雅普諾夫函數并且設計虛擬控制輸入[15-16],而真實控制輸入根據反饋設計,在遞推終端得到,最終基于李雅普諾夫穩定性理論得到系統受控穩定的充分條件。針對分數階Genesio-Tesi混沌系統,文獻[14]設計了反演控制器,使得分數階Genesio-Tesi主從混沌系統達到同步。文獻[17]討論了帶有未知參數的分數階Coullet混沌系統的同步問題,設計了自適應反演控制器。
另一方面,滑模變結構控制已經形成了一個相對獨立的研究分支,適用于線性與非線性系統、連續與離散系統、確定性與不確定性系統等,在實際工程中逐漸得到推廣應用。滑模控制在混沌系統的同步研究中也得到了應用,文獻[18]針對一類帶有外部擾動的分數階混沌系統,研究了自適應滑模同步問題;文獻[19]采用主動滑模控制探討了分數階主從結構混沌系統的同步問題。針對帶有時滯的分數階混沌系統,文獻[20]基于自適應模糊滑模控制研究了兩個不同的帶有不確定參數的分數階時滯混沌系統的同步問題。
自整數階Genesio-Tesi混沌系統在1992年提出以來[21],分數階Genesio-Tesi混沌系統也得到了眾多學者的重視。文獻[22]利用一個標量驅動信號,使得分數階Genesio-Tesi混沌系統達到同步;文獻[23]基于主動控制和滑模控制兩種方法,研究了分數階Genesio-Tesi混沌系統的混沌動態及其同步問題。雖然針對分數階Genesio-Tesi混沌系統的同步已有一些研究成果,但是基于反演滑模控制技術,實現分數階Genesio-Tesi混沌系統同步的研究仍然是一個空白。
本研究分析帶有參數不確定和外部擾動的分數階Genesio-Tesi混沌系統的結構特點,用反演設計方法在遞推過程中對Lyapunov子函數和虛擬控制輸入進行設計,并在反演終端加入滑模控制律,完成了能夠使帶有參數不確定和外部擾動的分數階響應系統與分數階驅動系統漸近同步的反演滑模控制器的設計。最后利用數值仿真驗證提出的分數階Genesio-Tesi混沌系統反演滑模同步算法的有效性。
1 分數階Genesio-Tesi混沌系統
由于Genesio-Tesi系統具備混沌系統的很多特征,因此成為混沌系統的代表之一。該系統包含了一個平方項和三個簡單的微分方程且微分方程取決于三個正實參數,其系統動態方程為
(1)
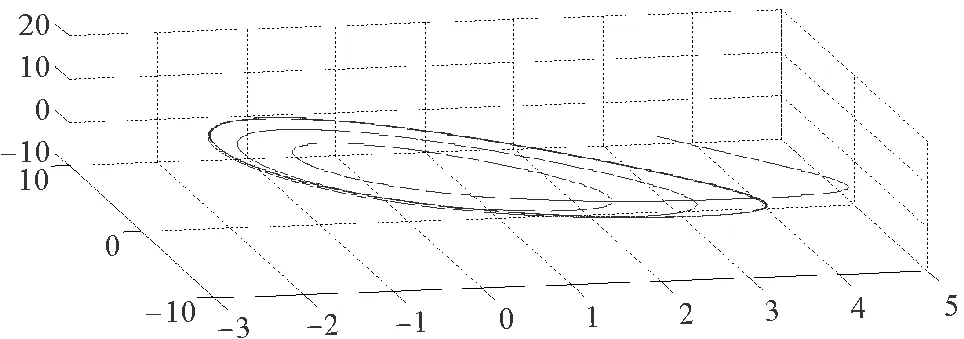
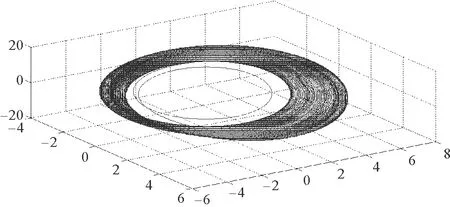
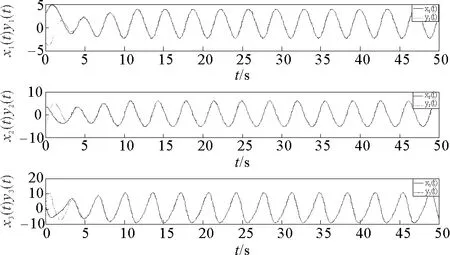
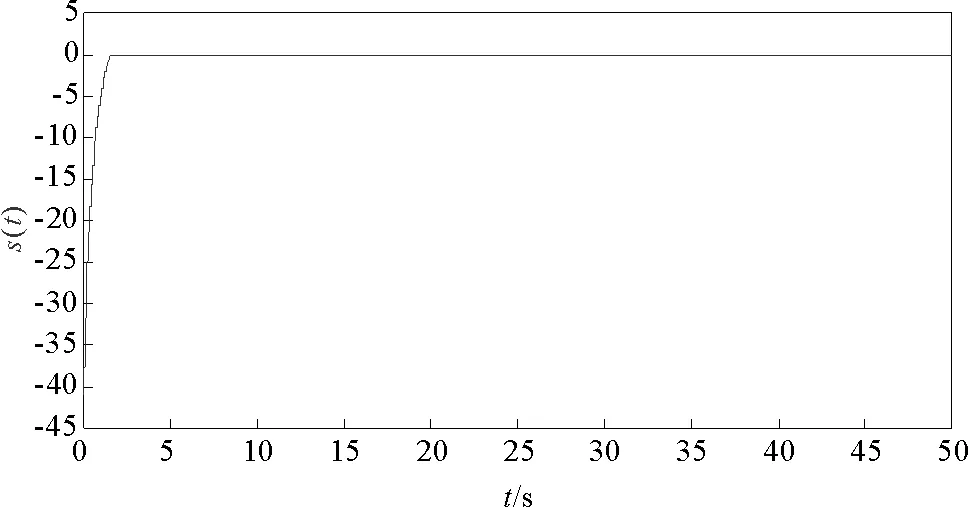
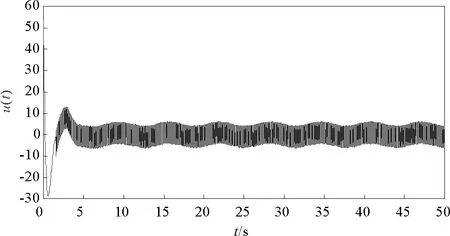
式中:x1,x2,x3是狀態變量;a,b,c是正實數且滿足ab 為了觀測Genesio-Tesi混沌系統的同步現象,設定系統(1)為驅動系統,作為系統(1)的響應系統的動態方程為 (2) 式中:y1,y2,y3是狀態變量;a,b,c是正實數且滿足ab 需要設計一個控制器u(t)來控制響應系統,使響應系統(2)與驅動系統(1)實現漸近同步。考慮到實際情況中不可避免地存在不確定項與外部擾動項,設計受控的響應系統: (3) 式中:y1,y2,y3是狀態變量;a,b,c是正實數且滿足ab 驅動系統(1)和受控響應系統(3)之間的誤差信號e(t)的數學模型如下: (4) 在控制器u(t)作用下,系統(3)與系統(1)實現漸近同步,也就是說誤差信號e(t)收斂至零。其誤差信號e(t)的動態模型如下: (5) 將分數階Genesio-Tesi混沌系統的模型描述為 (6) 式中:α為分數階且0<α≤1;x1,x2,x3是狀態變量;a,b,c是正實數且滿足ab 同理,由系統(2)可以得到系統(6)的響應系統的動態方程 (7) 其受控的分數階響應系統模型為 (8) 分數階驅動系統(6)與受控的分數階響應系統(8)之間的誤差信號動態方程為 (9) 分數階微分有三種最典型的定義,即Riemann-Liouvile定義、Grünwald-Letnikov定義和Caputo定義。由于在初始條件下,整數階微分方程沿用了相同的形式,所以Caputo定義已經被廣泛的應用于工程實踐。本文也采用Caputo定義來對特定的方程進行分數階微分。 定義1[1]對于一個連續的函數f,對其進行關于α階次的分數階求導定義如下 式中,Γ是伽馬函數并且滿足 引理1[24]如果x(t)∈Rn是微分函數的一個向量,則在時間t≥t0的任意時間里,下列關系恒成立。 式中,P∈Rn×n是一個常數對稱且正定的矩陣。 定理1帶有不確定參數和外部擾動的分數階響應系統(8)和分數階驅動系統(6)能夠達到漸近同步的條件是控制器u(t)設計如下: u(t)=ueq+uc =-[(3-a+x1+y1)e1+(5-b)e2+(3-c)e3 +Δf(y1,y2,y3)+d+k4s+k5sgn(s)], 式中, ueq=-[(3-a+x1+y1)e1+(5-b)e2+(3-c)e3+Δf(y1,y2,y3)+d], uc=-k4s-k5sgn(s)。 證明:首先定義一個Lyapunov函數,形式如下 , (10) 式中,z1=e1。 根據引理1,對式(10)進行階次為α關于時間的分數階微分求導,得到 (11) 接著,選取第二個Lyapunov函數,形式如下 (12) 式中,z2作為虛擬輸入且滿足z2=e1+e2。 根據引理1,對式(12)進行階次為α關于時間的分數階微分求導,得到 (13) 最后,選取第三個Lyapunov函數,形式如下 (14) 定義切換函數為 s=k1e1+k2e2+k3e3, (15) 式中,選取k1=2,k2=2,k3=1 根據引理1,對式(13)進行階次為α關于時間的分數階微分求導,得到 DαV3≤DαV2+sDαs (16) 將u(t)代入式(16),可得DαV3<0,則定理得證。 圖1 系統(6)的相軌跡Fig.1 Phase trajectory of system (6) 圖2 加入參數不確定與外部擾動的系統(6)的相軌跡Fig.2 Phase trajectory of the system (6)with uncertain parameters and external disturbance 本節通過數值仿真來驗證上述所設計的反演滑模控制器的有效性。 令α=0.97,a=1.2,b=2.92,c=6, k1=2,k2=2,k3=1,k4=2,k5=5, d=cos2t,Δf(y1,y2,y3)=0.2sin(2πy1)。 取初值為(x1(0),x2(0),x3(0))=(3,3,3),(y1(0),y2(0),y3(0))=(-3,-3,-5),圖1表示系統(6)的相軌跡圖,圖2表示考慮不確定性和外部擾動的系統(6)的相軌跡圖,圖3代表驅動系統(6)和響應系統(8)的狀態軌跡圖,圖4是同步誤差信號e(t)的響應圖,圖5~6分別表示滑模平面s(t)和控制輸入u(t)。可以看出,所設計的反演滑模控制器能夠保證驅動系統(6)和響應系統(8)的漸近同步。 圖3 受控的分數階驅動系統與響應系統的狀態軌跡Fig.3 State trajectories of the controlled fractional drive system and response system 圖4 同步誤差信號e1,e2,e3關于時間t的響應圖Fig.4 Synchronization errors e1,e2,e3 with time t 圖5 滑模平面s(t)關于時間t的響應Fig.5 Response of sliding surface s(t)with time t 圖6 分數階控制器u(t)狀態響應Fig.6 Response of controller u(t)with time t 研究了帶有參數不確定分數階Genesio-Tesi混沌系統的反演滑模同步問題,基于反演控制策略設計所給系統的李雅普諾夫子函數與虛擬控制輸入;然后在此基礎上設計滑模面,得到了能夠使帶有參數不確定與外部擾動的分數階響應系統與分數階驅動系統漸近同步的反演滑模控制器。最后,通過仿真驗證了所設計控制器的有效性。在后續的研究中,將針對分數階Genesio-Tesi混沌系統進行自適應模糊或自適應神經網絡控制與同步方面的研究。2 分數階Genesio-Tesi混沌系統的反演滑模同步
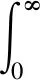
3 仿真算例

4 結論

