Δ源逆變器的小信號建模與無源器件參數(shù)影響分析

(1.山東科技大學 電氣與自動化工程學院，山東 青島 266590；2.哈爾濱工業(yè)大學 電氣工程及自動化學院，黑龍江 哈爾濱 150001)

Z源逆變器的出現(xiàn)在電力電子技術領域具有革命性的意義，目前廣泛應用于電機調速系統(tǒng)、分布式電源并網系統(tǒng)、電動汽車等領域。該逆變器直流電源與逆變橋之間由獨特的電感電容網絡聯(lián)接，這種網絡使得任意一個橋臂直通或者開路都不會對電源和開關器件造成影響。特殊的阻抗網絡使得逆變器適用于輸入電壓或電流有頻繁波動的場合，并且在各種功率變換中得到廣泛研究與應用，文獻[1-3]研究了其在DC/AC電能變換電路中的應用，文獻[4-5]將其應用于DC/DC變換電路，文獻[6]詳細闡述了其在AC/AC電路中的應用。同時一些改進的新型Z源逆變器也被廣泛研究[7-17]。

目前對于逆變器的功率等級要求越來越高，傳統(tǒng)Z源逆變器的升壓性能已經遠遠達不到應用要求，而且由于逆變器注入直通控制方式使得調制系數(shù)與直通占空比存在相互制約關系，一味調高直通占空比會使得調制系數(shù)較小，不利于輸出波形的優(yōu)化，輸出電壓含較多的諧波會加重濾波器的負擔，同時開關管承受了較高的電壓應力，所以傳統(tǒng)的Z源逆變器不適合電壓增益較大的場合。另外不連續(xù)輸入電流、巨大的起動電流等問題制約了Z源逆變器的應用。改進的準Z源逆變器具有連續(xù)輸入電流，也使得一個電容器的電壓應力減小[7-10]，但是仍然存在升壓能力不足的問題。為了克服這些缺陷，最近幾年含耦合電感網絡的新型逆變器得到廣泛研究，采用耦合電感網絡使逆變器可以在較低的直通占空比時仍能獲得較高的電壓增益，同時減少了電路元件數(shù)量，減小了逆變器的體積，具有更為廣闊的應用前景。

本研究在以上分析基礎上探討了一種具有新型耦合電感結構的Δ型電抗源逆變器，對該逆變器做出詳細的工作原理分析以及耦合電感網絡各元件對系統(tǒng)性能的影響分析，并且通過這些性能分析，根據(jù)電壓電流紋波要求得到電路參數(shù)選擇的一些規(guī)律，并用仿真和實驗結果驗證了得到的結論。

1 電壓型Δ型電抗源逆變器原理分析

圖1 AC-DC-AC電能變換Δ型電抗源逆變器電路拓撲Fig.1 Δ-type reactance-source inverter topology applied in AC-DC-AC power conversion

圖2 Δ型電抗源逆變器Fig.2 Δ-source inverter

2.1 電路拓撲和工作原理

圖1為Δ型耦合電感網絡應用于AC-DC-AC電能變換電路的電路結構圖。作為直流電源與逆變橋的中間升壓級電路，為了便于分析，將Δ型電抗源逆變器簡化等效為如圖2所示的工作原理圖，圖中將等效的勵磁繞組和漏感也表示出來。由于電路通常帶電感性負載或采用LC低通濾波器，因此在圖2中將逆變橋用電流源來代替。假定電路工作在理想狀態(tài)下，耦合電感具有非常高的耦合程度，公式推導時忽略圖中漏感和線圈繞組的影響。該逆變器有兩個穩(wěn)定的工作狀態(tài)：直通零狀態(tài)和非直通狀態(tài)。

當逆變器工作在直通零狀態(tài)時，電源端的二極管D1關斷，如圖2(a)所示。在這種狀態(tài)下，電容C2向耦合電感網絡充電，各繞組按匝數(shù)比的關系分配電壓，該過程中第三繞組將流過較大的電流，第一、二繞組流過的電流較小。可得直通零狀態(tài)下磁化電感上的電壓為：

(1)

其中，N1、N2、N3為耦合電感第一、二、三繞組的匝數(shù)。

當逆變器工作在非直通狀態(tài)時，如圖2(b)所示，電源端的二極管D1導通，電源和耦合電感網絡向負載供電，使輸出電壓升高。同時電源通過第二繞組向電容充電，此狀態(tài)第一、二繞組的電流較大，而第三繞組上的電流幾乎為零。同樣，可以求得非直通狀態(tài)下磁化電感上的電壓：

(2)

從公式(1)和(2)可以計算出電容C2的電壓。通過在一個開關周期內對磁化電感上的電壓應用伏秒平衡公式可列出：

vmTon+vmToff=0，

(3)

其中，Ton是一個周期T中的直通時間，Toff是非直通時間，考慮到理想三繞組耦合電感的電壓與繞組關系，即三個繞組的電壓與繞組匝數(shù)比相等，再根據(jù)繞組之間的基爾霍夫電壓定律可得出V1=V2+V3，由此推出繞組匝數(shù)的關系：

N1=N2+N3。

(4)

由公式(1)～(4)得電容電壓和直流鏈電壓平均值為：

(5)

其中，dst是開關直通占空比。可以很容易地通過計算非直通狀態(tài)的直流鏈電壓，來獲得Δ型耦合電感網絡的升壓因子G，非直通狀態(tài)下直流鏈電壓峰值為：

(6)

Δ型耦合電感網絡的升壓因子G為：

(7)

其中，KΔ是繞組系數(shù)，可以得出升壓因子與耦合電感網絡的KΔ以及dst的大小有關。若逆變電路的調制系數(shù)為M，可以推導出三相逆變器交流線電壓的峰值為：

(8)

由上面分析可知，Δ型電抗源逆變器有兩個可以調整的自由度來實現(xiàn)高電壓增益，既可以通過合理改變直通占空比的值，也可以通過改變繞組系數(shù)。而對于該類高增益逆變器來說，注入直通零狀態(tài)的控制方式決定了調制系數(shù)與直通占空比存在相互制約關系，這種制約關系從Z源逆變器開始就存在。而Δ型電抗源逆變器的優(yōu)勢就在于可以犧牲直通占空比來保持較大的調制系數(shù)，增大繞組系數(shù)來保持較高的電壓增益，這樣既不會影響電壓的升壓倍數(shù)，又使得開關管的電壓應力較小。

1.2 相關電路拓撲的升壓因子對比

表1給出了三種相關逆變器的參數(shù)對比。圖3給出了三種逆變器升壓能力曲線，可以看出整個曲線是非線性的，Δ型電抗源逆變器的升壓能力明顯優(yōu)于級聯(lián)boost型逆變器和Z源逆變器。圖4給出了對應于不同繞組系數(shù)KΔ下Δ型電抗源逆變器的升壓因子G關于直通占空比dst的關系曲線。由圖4可以看出，當選擇的繞組系數(shù)較大時，直通占空比的一個微小的變化就會導致升壓因子的巨大變化；而當選擇的繞組系數(shù)較小，直通占空比在較小的值變化時，升壓因子幾乎不變，可以根據(jù)實際應用需求合理地選擇相關參數(shù)。

2 Δ型電抗源逆變器的建模與無源器件參數(shù)的影響

2.1 電路的小信號模型

將應用小信號建模法對逆變器進行建模，求出變量的傳遞函數(shù),分析該新型逆變器的工作性能，包括動態(tài)響應、穩(wěn)定性等。小信號建模法是建立電路模型常用的方法，應用較為廣泛。因為電路中存在二極管、開關管等非線性元件，不能采用已有的線性分析理論，但是當時間基準取的無窮小時，這些非線性元件在某些時刻可以當成線性元件來處理，小信號建模法就是利用這一原理。考慮擾動信號作用下的電路運行狀態(tài)，將Δ型電抗源逆變電路等效為小信號電路。

表1 三種電路拓撲的參數(shù)對比Tab.1 Comparison of parameters of three circuit topologies

圖3 三種逆變器的升壓能力比較Fig.3 Comparison of boosting capability among three types of inverter

圖4 Δ型電抗源逆變器G-dst-K的關系圖Fig.4 Relationship of G-dst-K of Δ-source inverter

圖5 Δ型電抗源逆變器等效圖Fig.5 Δ-source inverter equivalent diagram

Δ型電抗源逆變器的升壓過程伴隨著電容和電感的充放電，而充放電的快慢直接決定了整個系統(tǒng)的響應速度。推導傳遞函數(shù)時應先建立交流小信號模型，因為Δ型電抗源逆變器適合應用在光伏電源等輸入直流電壓有波動的場合，因此本研究主要通過交流小信號建模法研究在輸入電壓有階躍變化的情況下電路中的電容對電路性能的影響，同時也對直通占空比發(fā)生變化時電路參數(shù)對系統(tǒng)的影響進行仿真分析。假設電路負載為感性，為了簡化分析，將逆變橋等效為一個開關管，電路如圖5所示。

圖5中瞬時值是由平均值加入擾動值構成的，滿足式(5)，可以看出擾動值是時變的，所以整個瞬時值也是時變的。

(9)

可以得到

(10)

其中，K是繞組系數(shù)，D是直通占空比，K′=N2/N3，D′=1-D，式(10)的等式右側有三個因子，第一個因子代表了電路的直流小信號模型，第二、三個因子代表了電路的交流小信號模型。電路如圖6所示。

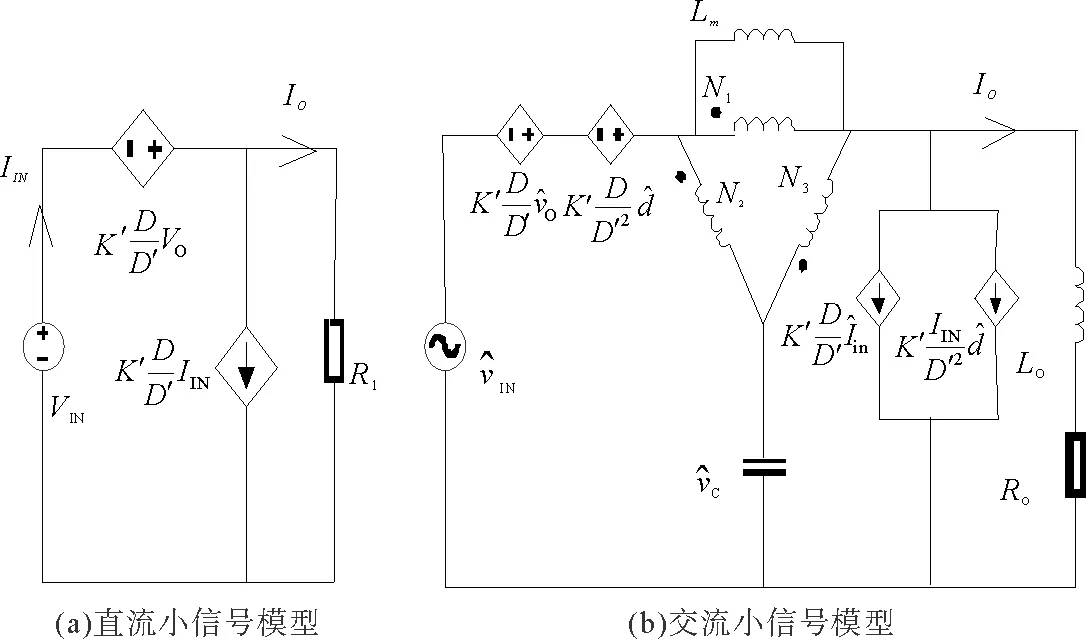
圖6 電路的小信號模型Fig.6 Small signal model of the circuit

得到輸入直流電壓到電容電壓的傳遞函數(shù)：

(11)

輸入直流電壓到輸出電壓的傳遞函數(shù)：

(12)

2.2 不同電容器參數(shù)下傳遞函數(shù)的Bode圖

下面研究電路電容器對于系統(tǒng)性能的影響。仿真電路的參數(shù)如下：N1∶N2∶N3=4∶3∶1，D=0.1，Lm=1 mH，L0=1 mH，R0=10 Ω。取三個數(shù)值的電容，分別是680、470、270 μF。將所有數(shù)據(jù)代入式(11)后，利用仿真軟件進行建模仿真，三種電容對應的傳遞函數(shù)的Bode圖如圖7和8所示。

從仿真結果可以看到系統(tǒng)的相角裕度是大于零的，所以利用Bode圖可以證明系統(tǒng)是穩(wěn)定的。需要注意的是，在受到擾動的時候電容量不同，曲線在中頻段的波形是不同的，系統(tǒng)表現(xiàn)的性能也不同。

圖7 電容電壓-輸入電壓傳遞函數(shù)的Bode圖Fig.7 Bode plot of the transfer function of the capacitor voltage to input voltage

圖8 輸出電壓-輸入電壓傳遞函數(shù)的Bode圖Fig.8 Bode plot of the transfer function of the output voltage to input voltage

一般來說，Bode圖的低、中頻段能間接地反映系統(tǒng)的性能。在系統(tǒng)的低頻段，三條曲線基本重合，而低頻段能間接反映系統(tǒng)的穩(wěn)定性，可以認為電容對系統(tǒng)的穩(wěn)態(tài)性能影響不大。中頻段與系統(tǒng)的暫態(tài)性能密切相關，觀察中頻段的波形可以發(fā)現(xiàn)，電容量越大曲線越靠下，實際表現(xiàn)為電容量越大對于系統(tǒng)的擾動越敏感。觀察三條曲線可以發(fā)現(xiàn)，電容量越小，相角裕度略微增大，增加了系統(tǒng)的帶寬，使系統(tǒng)的響應速度加快，超調量減小，系統(tǒng)更加穩(wěn)定。

圖9 電容電壓-輸入電壓傳遞函數(shù)的零極點圖Fig.9 Zero-pole plot of the transfer function of the capacitor voltage to input voltage

圖10 輸出電壓-輸入電壓傳遞函數(shù)的零極點圖Fig.10 Zero-pole plot of the transfer function of the output voltage to input voltage

由零極點圖9和10可以發(fā)現(xiàn)，隨著電容值的增大，兩個圖形中極點都沿著虛軸向坐標原點靠近。較大的電容將會降低系統(tǒng)的阻尼，經過較長時間才能達到新的穩(wěn)定狀態(tài)，并且會出現(xiàn)超調和振蕩現(xiàn)象，與Bode圖得出的結論基本一致。

2.3 無源元件參數(shù)對電路性能影響的仿真分析

上述兩個傳遞函數(shù)，都是電源電壓作為輸入量，由于直通占空比作為輸入量的傳遞函數(shù)的推導比較復雜且計算量很大，通過仿真來進行討論。另外，電感對于系統(tǒng)性能的影響也將在本節(jié)通過仿真研究。

外界的擾動主要考慮輸入直流電壓的躍變以及直通占空比的躍變，考慮這兩種擾動都具有實際意義。若是將Δ型電抗源逆變器應用于光伏發(fā)電系統(tǒng)，則前者可以模擬實際系統(tǒng)中太陽能電池所產生的直流電壓的波動，后者則可以模擬受到外界因素影響使得某一橋臂發(fā)生直通擾動的情況。

首先，保持電路中耦合電感網絡的匝數(shù)比不變，仿真中設定耦合電感的匝數(shù)比為60∶45∶15，運用Matlab/Simulink進行仿真，研究電容對于電路性能的影響。仿真結果如圖11和12所示，可以看出電容量越大，輸入直流電壓或直通占空比發(fā)生階躍變化時，輸出電壓振蕩越明顯，同時調整時間也越長，驗證了前面小信號建模法得出結論的正確性。因此，在電路升壓倍數(shù)滿足要求和電路正常工作的情況下，盡量取較小的電容值來改善電路的動態(tài)性能，但是也需要考慮使電容電壓紋波滿足系統(tǒng)的要求。

其次，保持電容量不變，分析耦合電感網絡的電感對系統(tǒng)的影響。

耦合電感網絡是Δ型電抗源逆變器用于升壓的核心部分，其正常運行對逆變器起著至關重要的作用。每匝線圈的電感值與匝數(shù)、磁芯形狀和材料都有關系。本研究中開關頻率較高，因此選擇性能優(yōu)良的錳鋅鐵氧體作為磁芯材料，一般磁導率在幾百到三萬之間，線圈匝數(shù)與電感滿足下列關系:

(13)

(14)

圖11 輸入電壓變化時電容對電路性能的影響Fig.11 Effect of capacitance on circuit performance during change in input voltage

圖12 直通占空比變化時電容對電路性能的影響Fig.12 Effect of capacitance on circuit performance during change in shoot-through duty ratio

圖13 輸入電壓變化時耦合電感網絡電感對電路性能的影響Fig.13 Effect of coupled inductor on circuit performance during change in input voltage

圖14 直通占空比變化時耦合電感網絡電感對電路性能的影響Fig.14 Effect of coupled inductor on circuit performance during chnge in shoot-through duty

表2 系統(tǒng)參數(shù)Tab.2 System parameters

在磁芯材料不變的情況下，耦合電感匝數(shù)越多，電感值越大，能夠為電路提供更加充沛的電能。電感一方面具有減緩啟動電流的作用，但另一方面又會使電路動態(tài)響應遲緩。在不考慮線圈漏感的情況下，通過三組電感值的仿真對比，可以發(fā)現(xiàn)電感的值越大，系統(tǒng)的最大超調量越小。大電感適合穩(wěn)定的電壓輸出，但隨著電感值變大，系統(tǒng)的調整時間同時會變得比較長，表現(xiàn)為系統(tǒng)電壓響應比較慢。由此可見，大電感可以使系統(tǒng)響應過程變得平緩，代價是延長系統(tǒng)的響應時間，所以在電感電流紋波滿足系統(tǒng)要求的前提下，要根據(jù)不同的負載需求來合理選擇電感的數(shù)值。大電感適合于要求穩(wěn)定輸出的負載，小電感適合于要求響應速度較快的負載，所以要合理選擇電感參數(shù)使得系統(tǒng)工作狀態(tài)最佳。另外在直通占空比變化的情況下，可以看到突變點附近波形會先向下運行一段時間，這種現(xiàn)象造成的原因是直通占空比-輸出電壓的傳遞函數(shù)存在一個位于虛軸右側的零點，導致這個系統(tǒng)變成了非最小相位系統(tǒng)。

3 樣機實驗與結果分析

根據(jù)電路原理圖搭建樣機模型，采用普通SPWM控制產生功率管直通信號，實驗電路如圖15所示，系統(tǒng)參數(shù)如表2所示，SPWM控制信號生成的仿真模型如圖16所示，輸出波形如圖17所示。當繞組系數(shù)等于3，直通占空比為0.1時，開關管電壓應力(直流鏈電壓)等于14.3 V，與理論推導結果一致。圖18給出了Δ源逆變器的效率，其大小受開關損耗和繞組損耗的影響較大。通過示波器測出的實驗波形如圖19(a)～(e)所示，其中輸出線電壓峰值和電容器電壓應力與由式(5)和式(8)計算的理論值稍有誤差，這是因為在搭建電路模型時，受到漏感和線圈電阻的影響，不可能做到電感的全耦合。從圖19(d)～(e)分析可知，當從非直通狀態(tài)向直通狀態(tài)變換時，二極管兩端將出現(xiàn)電壓過沖和震蕩，但幅值不大，對電路產生的影響較小。同樣，當直通狀態(tài)向非直通狀態(tài)轉換時，開關管兩端也會出現(xiàn)電壓過沖和震蕩，但經過很短的過渡時間就趨于穩(wěn)定。

圖15 Δ型電抗源逆變器實物圖與實驗圖Fig.15 Prototype of experimental circuit

圖16 SPWM控制信號生成仿真圖Fig.16 Simulation diagram of SPWM control signal generation

圖17 輸出波形M=0.9，D=0.1Fig.17 Output waveform at M=0.9,D=0.1

圖18 Δ型電抗源逆變器電路效率Fig.18 The efficiency of the Δ-source inverter

逆變器的工作效率定義為輸出功率/輸入功率。由圖18可以看出電路的效率將隨著直通占空比的提高而降低，造成這種情況的原因主要是直通電流過大造成了繞組損耗以及開關損耗增大，可以通過選擇性能優(yōu)良的線圈繞線和電路器件來減小電路損耗。

圖19 實驗結果Fig.19 Experimental results

4 結論

本研究在對新型Δ型電抗源逆變器進行詳細的工作原理分析的基礎上，得到電路的電壓增益關系。通過小信號建模法建立了系統(tǒng)的數(shù)學模型并求出相應的傳遞函數(shù)，畫出Bode圖和零極點圖，通過波形對比分析各無源元件對系統(tǒng)性能的影響，得到電路參數(shù)選擇的一些規(guī)律。Δ型電抗源逆變器除了繼承Z源逆變器的全部優(yōu)點之外，還具有以下優(yōu)勢：

1)通過獨特的三角形狀的耦合電感結構，可以實現(xiàn)靈活的升降壓功能，線圈電感的電流抑制作用使得啟動電流的影響很小。

2)能夠在較大的直通占空比下保持較小的開關電壓應力，同時也能夠在較小的直通占空比下仍保持較高的電壓增益。

3)具有較低的繞組損耗和繞組電壓降。Δ型電抗源逆變器具有更高的電路效率，較小的體積與重量。

但由于耦合電感不可避免的存在漏感，而漏感的存在對電路的工作過程會造成一定的影響，需要采取措施消除漏感的影響。因此，Δ型電抗源逆變器主要適用于要求電壓增益較高的應用場合，而Z源電路主要適用于電壓增益要求不是太高的應用場合。