濟南市地表水控制指標動態(tài)管理研究

李錫銅　曹升樂　劉陽　劉超

摘要：“三條紅線”是最嚴格水資源管理制度的核心，用水總量控制是“三條紅線”之首。用水總量控制指標由地表水控制指標和地下水控制指標兩部分組成。為研究地表水控制指標的動態(tài)管理方法，以國家分配的地表水用水總量控制指標為基礎，建立不同頻率年降水量與地表水控制指標的關系：利用馬爾可夫過程理論，推斷預報年的降水豐枯情況及年降水量，確定預報年的地表水控制指標：結合預報年年初地表水蓄水量，對預報年的地表水控制指標進行動態(tài)調(diào)整。以濟南市為例，給出了地表水控制指標動態(tài)管理過程，最終確定濟南市2017年地表水控制指標為2.39億_3，原制定濟南市2017年地表水控制指標為3.60億_3，兩者差異明顯。

關鍵詞：用水總量：控制指標：地表水;濟南市

中圖分類號：TV213.4

文獻標志碼：A

doi：10.3969/j.issn.1000- 1379.2019.03.016

水是生命之源，是人類生活和社會發(fā)展中無法替代的資源，也是生態(tài)系統(tǒng)中不可或缺的要素。隨著我國人口的增長與社會經(jīng)濟的發(fā)展，對水資源的需求越來越大，水資源缺乏問題日益突出。為此，2011年中央一號文件明確提出實行最嚴格水資源管理制度，制定用水總量、用水效率和水功能區(qū)限制納污“三條紅線”[1]。用水總量控制是“三條紅線”之首，用水總量控制指標的合理確定是水資源可持續(xù)利用、區(qū)域社會經(jīng)濟可持續(xù)發(fā)展的根本保障。

在取用水總量控制方面，國外部分學者對河流最大允許取水量進行了廣泛研究，如D.L.Blanc等[2]預測了撒哈拉沙漠南部地區(qū)未來的缺水量：L- Collet等[3]通過構建水資源綜合模型，評估了地中海地區(qū)中尺度流域的最大可供水量。“三條紅線”具有鮮明的中國特色，陳軍等[4]根據(jù)西雙版納地區(qū)的實際情況，構建了西雙版納“三條紅線”控制指標體系：陳方等[5]基于用水總量控制紅線，構建了太湖流域用水總量控制指標體系;劉淋淋等[6]通過對狹義、廣義及嚴格意義地表（地下）水資源可利用量的對比分析，提出了用水總量控制指標的確定方法。目前，我國各流域水行政主管部門建立了比較完善的水資源管理體系。黃河流域水量調(diào)度及用水總量控制的工作開展較早，為用水控制指標的制定提供了許多可供借鑒的經(jīng)驗[7]。

目前，我國各地區(qū)未來一段時間的用水總量控制指標均按國務院辦公廳2013年印發(fā)的《實行最嚴格水資源管理制度考核辦法》規(guī)定再分配得到，為一固定值。筆者認為該控制指標（特別是地表水的控制指標）應隨年降水量（地表水資源量）的豐枯而變化，同時受年初地表水蓄水量的影響。基于此，本文對地表水控制指標的確定方法進行研究。

1 地表水控制指標的確定方法

首先確定年降水量與地表水資源量的關系，根據(jù)分配的地表水控制指標，得到年降水量與地表水控制指標的關系：通過加權馬爾可夫模型預測年降水量，確定地表水控制指標：最后結合年初蓄水量對控制指標進行調(diào)整。

1.1 年降水量與地表水控制指標的關系

地表水資源量的多少取決于年降水量的大小，而地表水的控制指標應以地表水資源量為基礎。考慮到降水量年際差異，豐水年降水量大，對應的地表水資源量多，則地表水控制指標理論上應大一些：枯水年降水量小，對應的地表水資源量少，則地表水控制指標理論上應小一些。因此，首先分析年降水量與地表水動態(tài)控制指標的關系。

1.1.1 年降水量與地表水資源量關系確定

利用年降水量序列，用適線法確定年降水量頻率曲線，進而確定不同頻率的年降水量。據(jù)此建立年降水量與地表水資源量的關系方程，并推求不同頻率年降水量對應的地表水資源量。

1.1.2 年降水量與地表水控制指標關系確定

年降水頻率為50%即平水年時的降水量對應國家規(guī)定的地表水控制指標。年降水頻率小于50%（即豐水情況）時，地表水控制指標原則上由地表水資源可利用量確定，以年降水頻率5%（豐水年上限值）時對應的地表水資源量的40%為地表水控制指標的上限值：年降水頻率為5% - 50%時，地表水控制指標呈線性變化，起點為地表水的控制指標，終點為地表水控制指標的上限值。年降水頻率大于50%（即枯水情況）時，地表水控制指標原則上由地表水可供水量確定。分別確定年降水頻率75%（偏枯年降水量）和95%（枯水年下限值）時的可供水量，即為年降水頻率為75%和95%時對應的地表水控制指標。年降水頻率為50% - 75%和75%- 95%時，地表水控制指標同樣呈線性變化。因此，降水頻率從95%到5%，年降水量與地表水控制指標的關系為3段分段函數(shù)。

1.2 年降水量預測

在制定用水控制指標時需要對當年的降水情況進行預測。年降水量序列可以通過多元線性回歸[8]、灰色系統(tǒng)[9]、人工神經(jīng)網(wǎng)絡[10]、馬爾可夫模型、模糊理論[11]等數(shù)值模擬方法來進行預測。相對于其他預測方法，馬爾可夫模型是典型的定量預測方法，適用于中短期預測，且預測結果精度較好[12]，因此本文采用馬爾可夫模型來預測年降水量的豐枯情況。

1.2.1 馬爾可夫模型介紹

馬爾可夫模型是一種以概率論和隨機過程理論為基礎，運用數(shù)學模型來分析客觀對象發(fā)展變化過程的一種方法[13]。它最重要的特點是“無后效性”，要確定將來的狀態(tài)，只需知道現(xiàn)在的狀態(tài)即可。馬爾可夫模型的統(tǒng)計特性完全由它的初始分布和轉(zhuǎn)移概率確定[14]。對于離散型序列有：

1.2.2 馬爾可夫模型預測年降水量的基本步驟

（1）區(qū)間的劃分及豐枯狀態(tài)確定。用均值標準差法將降水序列分為枯水、偏枯、平水、偏豐和豐水5個狀態(tài)，分別對應空間狀態(tài)1、2、3、4、5。

（2）轉(zhuǎn)移矩陣的確定。按上述分級標準確定降水序列中各年降水量所對應的狀態(tài)，利用式（1）和式（2）對所得的結果進行統(tǒng)計計算，可得不同步長馬爾可夫模型的轉(zhuǎn)移概率矩陣。

（3）計算年降水序列的各階自相關系數(shù)“及各步長的權重w_k。

自相關系數(shù)r_k計算公式為

1.2.3 均值標準差法

水文序列的豐枯區(qū)間劃分有很多種方法，如要素距平值法、均值標準差法、保證率法、集對分析法等。結合各方法優(yōu)缺點、適用性及研究區(qū)實際情況，本文采用均值標準差法。

均值標準差法同時考慮了均值和方差的影響，其通用劃分標準為x+bs（x為水文序列均值、s為水文序列標準差、b為系數(shù)）。

運用均值標準差法將豐枯狀態(tài)按照枯水、偏枯、平水、偏豐、豐水5級劃分，常見劃分標準見表1。

1.3 地表水控制指標的動態(tài)調(diào)整

根據(jù)預測的年降水量確定當年地表水控制指標后，需對該指標進行調(diào)整。地表水用水指標的確定不僅要考慮年降水量的影響，而且應反映年初蓄水量的多少，地表水蓄水量用水庫與湖泊的蓄水量來表示。

分析年初地表水蓄水量長序列資料，確定年初地表水合理的蓄水量值（可采用地表水年初蓄水量的多年平均值）。當年初的地表水蓄水量小于合理的蓄水量時，應適當減小當年地表水指標：當年初的地表水蓄水量大于合理的蓄水量時，可適當增加當年地表水指標。減小（或增大）的具體值應以年初地表水蓄水量對應的可利用量為基礎綜合確定，同時考慮蒸發(fā)和滲漏的影響。

依據(jù)預測得到的年降水量推求地表水控制指標，并結合年初蓄水量對控制指標進行調(diào)整的方法稱為地表水控制指標的動態(tài)管理方法。

2 應用實例

以山東省濟南市為例，對2017年地表水控制指標進行動態(tài)管理研究。濟南市水資源主要來自大氣降水和過境河流，由當?shù)氐乇硭⒌叵滤涂退M成。濟南市水資源具有總量不足、年際變化大、年內(nèi)分配不均和地域分布不均等特點。濟南市為資源性缺水地區(qū)，是全國重點缺水城市之一。濟南市多年平均降水量為645.6 mm，多年平均水資源量為15.70億m³，其中地表水資源量為7.94億m³。由山東省用水總量控制指標確定的濟南市2017年地表水的控制指標為3. 60億m³。

2.1 濟南市年降水量與地表水控制指標的關系

2.1.1 濟南市年降水量與地表水資源量的關系

濟南市2000-2016年年降水量與地表水資源量的關系見圖1，用各種線形進行分析、擬合，結果表明一次函數(shù)的擬合度最高。推求出的年降水量與地表水資源量的回歸方程為

y= 0.028 5x - 10.622 （R²= 0.936 8）

（6）

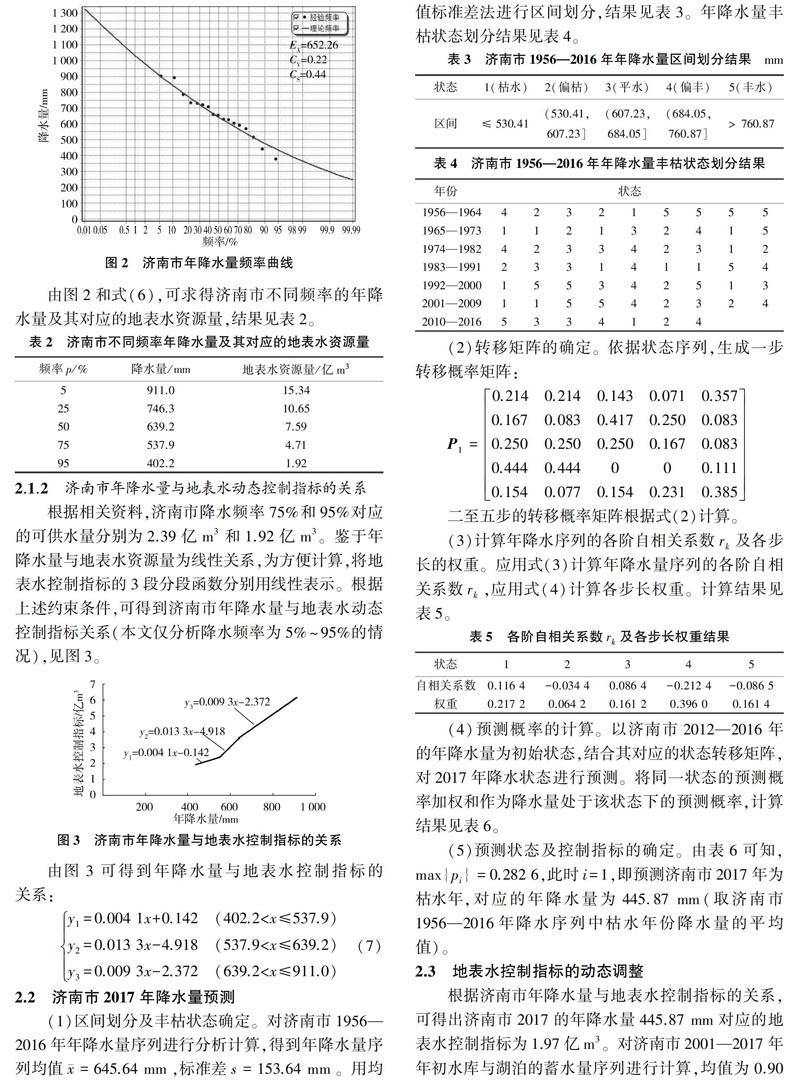
利用濟南市1956-2016年降水量序列，確定降水量頻率曲線，適線結果見圖2。

由圖2和式（6），可求得濟南市不同頻率的年降水量及其對應的地表水資源量，結果見表2。

2.1.2 濟南市年降水量與地表水動態(tài)控制指標的關系

根據(jù)相關資料，濟南市降水頻率75%和95%對應的可供水量分別為2.39億m³和1.92億m³。鑒于年降水量與地表水資源量為線性關系，為方便計算，將地表水控制指標的3段分段函數(shù)分別用線性表示。根據(jù)上述約束條件，可得到濟南市年降水量與地表水動態(tài)控制指標關系（本文僅分析降水頻率為5% - 95%的情況），見圖3。

由圖3可得到年降水量與地表水控制指標的關系：

Yi= 0.004 lx+0.142 （402.2

y2= 0.013 3x-4.918 （537.9

y3= 0.009 3x-2.372 （639.2

2.2 濟南市2017年降水量預測

（1）區(qū)間劃分及豐枯狀態(tài)確定。對濟南市1956-2016年年降水量序列進行分析計算，得到年降水量序列均值x= 645.64 mm，標準差s=153.64 mm。用均值標準差法進行區(qū)間劃分，結果見表3。年降水量豐枯狀態(tài)劃分結果見表4。

（2）轉(zhuǎn)移矩陣的確定。依據(jù)狀態(tài)序列，生成一步轉(zhuǎn)移概率矩陣：

二至五步的轉(zhuǎn)移概率矩陣根據(jù)式（2）計算。

（3）計算年降水序列的各階自相關系數(shù)r_k及各步長的權重。應用式（3）計算年降水量序列的各階自相關系數(shù)r_k，應用式（4）計算各步長權重。計算結果見表5。

（4）預測概率的計算。以濟南市2012-2016年的年降水量為初始狀態(tài)，結合其對應的狀態(tài)轉(zhuǎn)移矩陣，對2017年降水狀態(tài)進行預測。將同一狀態(tài)的預測概率加權和作為降水量處于該狀態(tài)下的預測概率，計算結果見表6。

（5）預測狀態(tài)及控制指標的確定。由表6可知，max{pi}=0.282 6，此時i=l，即預測濟南市2017年為枯水年，對應的年降水量為445. 87 mm（取濟南市1956-2016年降水序列中枯水年份降水量的平均值）。

2.3 地表水控制指標的動態(tài)調(diào)整

根據(jù)濟南市年降水量與地表水控制指標的關系，可得出濟南市2017的年降水量445.87 mm對應的地表水控制指標為1.97億m3。對濟南市2001-2017年年初水庫與湖泊的蓄水量序列進行計算，均值為0.90億m³：濟南市2017年年初水庫與湖泊的蓄水量為1.42億m³（考慮蒸發(fā)與滲漏的影響，系數(shù)為0.8），地表水控制指標可增加0.42億m³。因此，最終確定濟南市2017年地表水控制指標為2.39億m³，與根據(jù)山東省用水總量控制指標確定的濟南市2017年地表水控制指標為3.60億m³相比少了1.21億m³，說明年降水量以及年初水庫與湖泊的蓄水量對地表水控制指標的影響較大，地表水控制指標的動態(tài)管理研究有實際意義。

3 結語

（1）以國家分配的地表水用水總量控制指標為基礎，通過研究預報年的降水年型和地表水年初蓄水量對地表水控制指標的影響，提出了地表水控制指標的動態(tài)管理方法。并以濟南市為例，對其2017年地表水資源量的控制指標提出了具體調(diào)整方案。通過調(diào)整后的地表水控制指標與原分配指標進行對比可以看出，兩者差異明顯，說明地表水控制指標的動態(tài)管理研究有實際意義。

（2）地表水控制指標的動態(tài)管理方法適用于我國北方大部分地區(qū)，對于充分利用地表水資源、保障地區(qū)社會經(jīng)濟的可持續(xù)發(fā)展具有十分重要的現(xiàn)實意義，對其他地區(qū)地表水總量控制指標的制定具有借鑒意義。

（3）地表水控制指標的確定受多種因素的影響，目前這方面的研究成果不多。本文僅考慮了預報年的降水年型和年初地表水蓄水量，下一步需要對該方法進行深入研究。

參考文獻：

[1]王浩，實行最嚴格水資源管理制度關鍵技術支撐探析[J].中國水利，2011（6）：28-29.

[2]BLANC D L，PEREZ R.The Relationship Between Rainfalland Human Density and Its Implications for Future WaterStress in Sub-Saharan Africa[J].Ecological Economics，2008，66（2）：319-336.

[3]Collet L，Ruelland D， Borrellestupina V， et al.IntegratedModelling to Assess Long-Term Water Supply Capacity of aMeso-Scale Mediterranean Catchment[J]. Science of theTotal Environment， 2013， 461-462（7）：528-540.

[4] 陳軍，楊國勝，武曉文，等，西雙版納最嚴格水資源管理“三條紅線”控制指標體系研究[J].水電與新能源，2014（3）：6—9.

[5]陳方，盛東，高怡，等，太湖流域用水總量控制體系研究[J].水資源保護，2009，25（3）：37-40.

[6]劉淋淋，曹升樂，于翠松，等，用水總量控制指標的確定方法[J].南水北調(diào)與水利科技，2013，11（5）：159-163.

[7]孔祥磊，黃河山東段河道治理與工程質(zhì)量控制研究[D].濟南：山東大學，2012：27-47.

[8]張曉偉，黃領梅，沈冰，等，灰色自記憶神經(jīng)網(wǎng)絡模型在年徑流預測中的應用[J].西安建筑科技大學學報（自然科學版），2006，38（6）：761-764.

[9]鄧聚龍，灰色系統(tǒng)基本方法[M].武漢：華中理工大學出版社，1987：74-89.

[10]張青貴，人工神經(jīng)網(wǎng)絡導論[M].北京：中國水利水電出版社，2004：67-81.

[11]楊綸標，高英儀，凌衛(wèi)新，模糊數(shù)學原理及應用[M].5版，廣州：華南理工大學出版社，2011：52-76.

[12] 馮朝山，基于加權馬爾可夫模型的降水預測研究[J].人民黃河，2009，31（4）：31-33.

[13]馮虹，鄒華，魏文元，馬爾可夫鏈在教學質(zhì)量評價中的應用[J].天津師范大學學報（自然科學版），1999，l9（1）：6-10.

[14]朱寧，李竹梅，馬爾可夫過程在教學管理中的應用[J].桂林電子工業(yè)學院學報，2000，20（2）：74-77.