基于遺傳算法的混合Copula函數的時段洪量估計
劉立燕 解培中 王穎


摘要:淮河流域下游入江水道,每年雨水充足,容易引發洪水,對人民生命及財產安全造成威脅,因此對洪水特征變量——洪峰流量與整個洪水過程洪量的估計以及防洪工程的建設提出更高的要求。利用混合Copula函數將洪峰流量與時段洪量進行聯合分析,利用基于遺傳算法的優化適線法計算出淮河下游入江口的中渡水文站洪峰流量與時段洪量離差平方和最小時的Frank Copula、Clayton Copula、Cumbel Hougaard Copula的函數組合,在此基礎上根據洪峰值利用邊緣分布與聯合分布之間的關系推求出時段洪量,為防洪工程設計提供參考。對中渡水文站實測數據的分析結果表明:采用混合Copula函數比采用單- Copula函數更精確,并且混合Copula函數具有靈活性,能夠較好地擬合兩變量的相關關系。
關鍵詞:水文學;遺傳算法;混合Copula;聯合分布;中渡水文站;淮河
中圖分類號:TV122+.5
文獻標志碼:A
doi:10.3969/j .issn.1000- 1379.2019.03.012
1 研究背景
洪水是自然界中最危險的自然災害之一.影響的范圍非常大。據報道,每年洪水引起的損失占自然災害總損失的40%左右。在世界范圍內洪水預測已經逐漸成為廣泛研究的課題,尤其對于洪水高發區的人民來說,準確預測洪水并且提前給予當地居民警告是非常有必要的。
傳統的頻率分析方法都是基于單一特征變量的頻率分析對洪水發生的概率進行分析,即先假定某一特征變量符合某一分布線型,之后對分布線型中的參數進行估計[1-3].但單變量頻率分析忽略了同一事件中其他特征變量的影響。為此,進一步提出了多變量頻率分析方法,如Copula函數頻率分析方法。最近幾十年,Copula函數在金融、保險、財經風險等方面的應用較為廣泛[4-5]。水文現象中的隨機性與上述幾個方面相似,因此Copula函數在水文研究中的應用應運而生。
Copula函數是將多個單變量概率分布函數連接起來的多變量分布函數,利用Copula分布函數無需考慮各個單變量的概率分布函數。首次將Copula函數應用在水文領域的是De Michele與Salvadoria[6],之后國內外相繼利用Copula函數進行水文頻率分析。文獻[7]將Copula函數應用于降水概率的預測中,把年降水均值和年降水極值均值作為兩個研究變量,利用Pearson -Ⅲ型分布推求各變量的邊緣分布,然后通過Copula函數構建其聯合分布,對降水情況進行分析;文獻[8]研究了序列長度對Copula函數擬合效果與不確定度的影響;文獻[9]將歷史洪水考慮在內,然后利用Copula函數進行分析;文獻[10]利用Copula函數將洪峰流量、洪量、歷時分布進行聯合,推求出RomaineRiver洪水發生情況;文獻[II]采用不同類型的Copula函數對Save River的Litijia觀測站58場洪水進行模擬,結果表明幾種類型Copula函數的模擬結果差別不大;文獻[12]將Copula函數應用于大壩設計,通過模擬大壩的不同洪水強度對應的回歸周期,為大壩設計提供風險參考;文獻[13]收集分析了加拿大不同氣候區的21個流域的洪水特征值,并利用ClaytonCopula函數模擬這21組洪水特征值,分析了氣候變化對洪水的影響。然而上述研究都是針對單- Copula函數進行分析,并沒有考慮混合Copula函數的靈活性。在金融領域混合Copula函數得到廣泛應用,文獻[14]利用混合Copula函數將不同市場聯合起來,并利用EM算法求出混合Copula函數的權重及其相關參數,結果表明混合Copula函數更能夠描述兩者之間的相依結構;文獻[15]提出了M-Copula-EGARCH -M投資組合模型,結果表明混合Copula函數能夠較好地捕捉兩個市場間的關系。文獻[16]首次將混合Copula函數應用在洪水遭遇問題分析中,利用優化適線法確定混合Copula函數的參數,分析了長江干流的設計洪峰流量,并驗證了該方法的可行性。
本文在文獻[14-16]的基礎上提出了一種基于遺傳算法的混合Copula函數的參數估計方法,并利用洪峰與時段洪量建立混合Copula函數模型,最后利用該模型以及洪峰邊緣分布函數估計整個洪水過程的洪量。
2 混合Copula函數估計方法
2.1 Copula函數簡介
二維Copula函數簡述為[17]
2.3 基于遺傳算法的混合Copula函數的參數估計
遺傳算法是基于自然選擇和遺傳學概念的隨機優化算法,首先產生一個種群,種群中的每個個體代表給定目標函數的初始解:其次通過適應度函數來評價各個個體的適應性,并通過適應度來決定當前種群個體遺傳到下一代群體中的機會多少:然后對遺傳到下一代的個體進行選擇、交叉,產生新的種群;最后更新遺傳代數,直至滿足終止條件。具體步驟如下[19]。
(1)初始化種群。
(2)利用選擇函數從種群中選擇父輩。
(3)對所選擇的父輩進行交叉,產生下一代個體。
(4)對個體進行突變。
(5)更新遺傳代數。
(6)當不滿足最大遺傳代數時,重復執行(2)(3)(4)(5)操作。
(7)結束。
本文利用遺傳算法計算出理論Copula函數與經驗Copula函數離差平方和(O/S)最小時在式(5)的約束下式(4)中各個參數的值。具體計算步驟如下。
當選取的γ值較小時,可能不滿足ω1+ω2+ω3=1,適應度函數已經達到極小值點,造成約束條件失去意義,因此γ要盡可能選擇合理,避免不滿足約束條件,且不影響目標函數的最值選擇。
(3)確定最大遺傳代數Gm以及交叉概率pc。確定懲罰因子γ后,通過描繪適應度函數取得最小值min (fs)時隨著最大遺傳代數改變的圖像,選擇合適的最大遺傳代數:當最大遺傳代數以及適應度函數確定之后,通過改變交叉頻率繼續對所求函數進行優化,進一步描繪min (fs)與不同交叉概率之間的圖像,選擇合適的交叉概率,保證優化值為最小值。
(4)利用選定的遺傳算法的參數計算出混合Copula函數的各個參數值。
2.4 混合Copula函數的估計步驟[22]
首先利用混合Copula函數將兩變量X、Y的邊緣分布函數連接起來,構建X、Y的聯合分布函數:其次在已知t+l時Xt+1的條件下,基于混合Copula函數建立Y的邊緣分布與聯合分布的關系式:最后計算因變量Y在t+l時的值Yt+1。具體步驟如下。
3 實例分析
淮河流域下游人江水道,汛期雨水充足,容易引發洪水,對人民生命及財產安全造成威脅,因此對洪水特征變量——洪峰流量與整個洪水過程的洪量估計以及防洪工程建設提出更高的要求。以淮河流域下游中渡水文站1962-2014年的洪峰流量與整個洪水過程的3d洪量作為研究對象,令洪峰流量為自變量X,3d洪量為因變量y。選取1962-2010年的洪峰流量與時段洪量進行聯合分析計算并建立模型,通過建立的模型,以2011-2014年洪峰流量為自變量,推求相對應的時段洪量,作為檢驗模型的依據。
首先依據1962-2010年的洪峰流量與時段洪量數據,利用核函數法估計出洪峰流量與時段洪量的邊緣分布值,各個變量的邊緣分布見圖1、圖2。
其次確定遺傳算法的適應度函數的懲罰因子γ、最大遺傳代數Gm以及交叉概率pc。
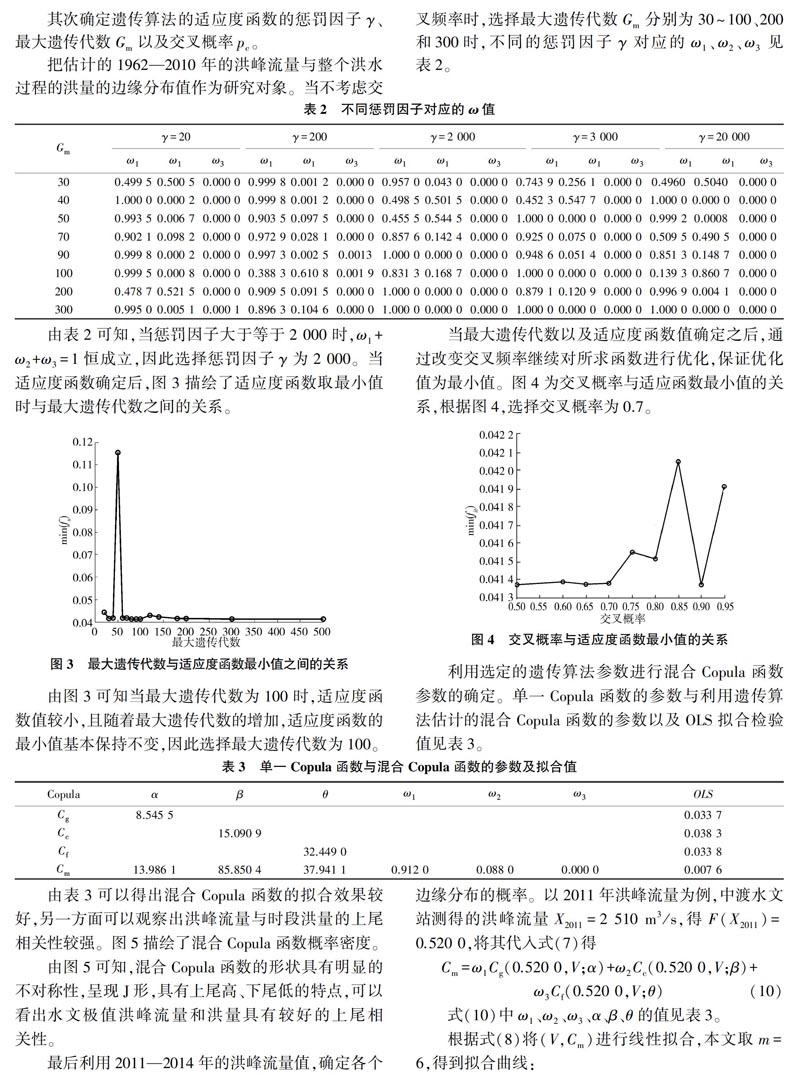
把估計的1962-2010年的洪峰流量與整個洪水過程的洪量的邊緣分布值作為研究對象。當不考慮交叉頻率時,選擇最大遺傳代數Gm分別為30 - 100、200和300時,不同的懲罰因子γ對應的ω1、ω2、ω3見表2。
由表2可知,當懲罰因子大于等于2 000時,ω1+ω2 +ω3=1恒成立,因此選擇懲罰因子γ為2 000。當適應度函數確定后,圖3描繪了適應度函數取最小值時與最大遺傳代數之間的關系。
由圖3可知當最大遺傳代數為100時,適應度函數值較小,且隨著最大遺傳代數的增加,適應度函數的最小值基本保持不變,因此選擇最大遺傳代數為100。
當最大遺傳代數以及適應度函數值確定之后,通過改變交叉頻率繼續對所求函數進行優化,保證優化值為最小值。圖4為交叉概率與適應函數最小值的關系,根據圖4,選擇交叉概率為0.7。
利用選定的遺傳算法參數進行混合Copula函數參數的確定。單一 Copula函數的參數與利用遺傳算法估計的混合Copula函數的參數以及OLS擬合檢驗值見表3。
由表3可以得出混合Copula函數的擬合效果較好,另一方面可以觀察出洪峰流量與時段洪量的上尾相關性較強。圖5描繪了混合Copula函數概率密度。
由圖5可知,混合Copula函數的形狀具有明顯的不對稱性,呈現J形,具有上尾高、下尾低的特點,可以看出水文極值洪峰流量和洪量具有較好的上尾相關性。
最后利用2011-2014年的洪峰流量值,確定各個邊緣分布的概率。以2011年洪峰流量為例,中渡水文站測得的洪峰流量X2011=2 510 m3/s,得F(X2011)=0.520 0.將其代人式(7)得
由圖6可以看出兩函數的交叉點為(x,y)=( 0.534 0,0.518 2),即此時V= 0.534 0。
此時利用MATLAB中的ginput()[],從圖2中觀察可知,當V=F(y)= 0.534 0時,對應的Y值為5.306。實際時段洪量為5.478億m3,誤差為-3. 1%。為了進一步分析混合Copula函數的性能與估計能力,利用單一的Copula函數進行估計,計算過程同理可得。2011-2014年的實測整個洪水過程的洪量與利用各模型估計出的整個洪水過程的洪量,相對誤差與平均相對誤差(歷年誤差的絕對值的平均值)見表4。
4 結語
混合Copula函數具有較好的靈活性,能夠更好地描繪洪峰流量與整個洪水過程的洪量的相互關系:利用洪峰流量與時段洪量之間的相互關系,在已知洪峰流量的情況下利用混合Copula函數可以更好地估計整個洪水過程的洪量。但是本文利用遺傳算法對混合Copula函數的參數進行估計時,由于遺傳算法的特性,可能陷入局部最優,因此應該合理調整遺傳代數以及選擇概率。同時,對于懲罰參數的選擇應該多次嘗試,避免計算出來的值不滿足約束條件。
參考文獻:
[1]鮑振鑫,水文頻率分析適線法參數估計研究[D].南京:南京水利科學研究院,2010:33-48.
[2]周川,陳元芳,魏琳,等,適線法在洪水超定量系列頻率分析中的應用研究[J].水電能源科學,2011,29(3):48-50.
[3] 趙璧奎,王麗萍,李繼清,等,不連續系列的P-m型曲線計算機適線法探討[J].水電能源科學,2012,30(3):64-67.
[4]AAS K,CZADO C,FRICESSI A,et al.Pair-Copula Con-structions of Multiple Dependence [J]. InsuranceMathematics&Economics, 2009, 44(2):182-198.
[5] TSUKAHARA H.Semiparametric Estimation in Copula Models[J]. Canadian Journal of Statistics, 2005, 33(3):357-375.
[6]MICHACLE D C,SALVADORI G.A Ceneralized Pareto In-tensityduration Model of Storm Rainfallexploiting 2- Copulas[J]. Journal of G eophysical Research Atospheres, 2003, 108(D2):171-181.
[7] 倪增華,劉合香,羅彥麗,等.Copula函數在廣西洪澇災害的降水概率預測中的應用[J].氣象研究與應用,2014,35(2):32-39.
[8] 童心.Copula函數與信息熵理論在洪水多元分析和徑流隨機模擬中的研究[D].南京:南京大學,2015:36.
[9] L1 T,GUO S,CHE N L,et aI.Bivariate Flood Frequency A—nalysis with Historical Information Based on Copula[J].Joumal of Hydrologic Engineering-ASCE, 2013, 18(8):1018-1030.
[10]PARENT E,FAVRE A C,BERNIER J,et aI.Copula Modelsfor Frequency Analysis What can be Leamed from a Bayes-ian Perspective[J].Advanced in Water Resources, 2014, 63(2):91-103.
[11]SRAJ M,BEZAK N,BRILLY M.Bivariate Flood FrequencyAnalysis Using the Copula Function:a Case Study of theLitija Station on the Sava River[J].Hydrological Processes,2015,29(2):225-238.
[12]REQUENA A I,MEDIERO L,GARROTE LA Bivariate RetumPeriod Based on Copulas for Hydrologic Dam Design Accountingfor Reservoir Routing in Risk Estimation[J].Hydrology andEarth System Sciences ,2013, 17(8):3023-3088.
[13] JEONC D, SUSHAMA L,KHALIQ M N, et al.A Copula-Based Multivariate Analysis of Canadian RCM ProjectedChanges to Flood Characteristics for Northeastem Canada[J] .Climate Dynamics, 2014, 42( 7-8):2045 - 2066.
[14] 馬梅,盧俊香,杜艷麗,混合Copula模型選擇及其應用[J].價值工程,2017,36(1):191-194.
[15] 申建平,基于M-Copula函數的投資組合和相關風險研究[D].重慶:重慶大學,2014:144-166.
[16] 王占海,陳元芳,黃琴,等.M-Copula函數在洪水遭遇中的應用研究[J].水電能源科學,2009, 27(1):69-73.
[17] NELSEN R B.An Introduction to Copulas[M].Cermany:Springer Publishing Company, Incorporated, 2010:315.
[18] 韋艷華,張世英,郭焱,金融市場相關程度與相關模式的研究[J].系統工程學報,2004, 19(4):355-362.
[19]BODENHOFER U.Cenetic Algorithms: Theory and Appli-cations[J].Lecture Notes, 1993: 1-3.
[20]Ozgur Yeniay. Penalty Function Methods for Constraint Op-timization with Cenetic Algorithms[J].Mathematical&Computational Applications, 2005,10(1):45 - 56.
[21]王文圣,水文學不確定性分析方法[M].北京:科學出版社,2011:110-125.
[22] 陳晶,王文圣.Copula預測方法及其在年徑流預測中的應用[J].水力發電學報,2015, 34(4):16-21.

