理論單位線曲線族數學公式的提出
宋雅坪,房國忠,徐 崢,郭希海,孫 羽
(國家電網公司 東北分部,沈陽 110000)
1 概 述
洪水經驗單位線是傳統的洪水匯流預報方法[1],雖然方法簡單,應用也很廣泛,但預報時單位線的選取因人而異,預報結果的精度難以控制[2-3]。同時,經驗單位線的分割與制作過程十分繁瑣,難以達到理想完備的程度[4-5]。更重要的是經驗單位線只能從已發生的洪水過程當中獲得有限的(常見)洪水信息,對于未發生的罕見特大洪水的預報,由于缺少相應的外推單位線,極有可能存在洪峰預報嚴重偏小的重大安全隱患(即經驗單位線缺乏外延遞推性)[6-8]。能否找到一個理想完備的洪水徑流單位線數學公式,使預報能夠連續覆蓋從極枯到極豐整個可能出現的土壤濕度狀態(具有外延遞推性),且其預報結果滿足高精而穩定的要求,這是水文基礎理論研究方面需要解決的基本問題[9]。
本文創立的理論單位線曲線族數學公式,為預報理論的實際應用提供了一種新的數學工具。期待該成果與產流預報模式相結合,在高精度預報模型中得到廣泛的應用。
2 徑流過程的圖形描述
洪水徑流過程是一個漲水段短、退水段很長的時序流量過程。當流域土壤干旱和降雨小時,產流少,洪水過程為矮胖型(洪峰漲幅小、洪水歷時長);反之,當流域土壤濕潤和降雨大時,產流多,洪水過程為尖瘦型(洪峰漲幅大、洪水歷時短)。徑流過程典型曲線見圖1。
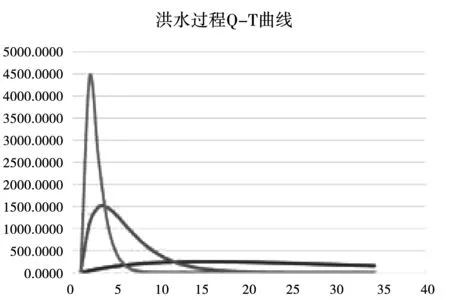
圖1 徑流過程典型曲線
3 洪水徑流數學描述需解決的問題
3.1 尋求洪水徑流過程Q-T曲線的數學公式
先要找到一個數學公式能夠描述某一次洪水過程的完整形態。
3.2 驗證洪水徑流過程Q-T數學曲線族的代表性與完備性
在找到一個洪水徑流數學公式的基礎上,尋求一組洪水徑流過程Q-T曲線族,其等分或非等分變化要與流域不同干濕程度的相應實際洪水單位線一一匹配,即理論單位線具有真實反映洪水徑流豐枯變化的全過程(完備性),同時具有理論外延的合理性。
本文將試圖通過指數函數的初等運算來解決這一復雜的匯流模式理論問題。
4 徑流匯流模式的數學描述
4.1 徑流過程的數學描述
洪水徑流過程能否用數學公式來描述?如果能找到一個公式或初等函數來完整地反映洪水過程,不僅是一個十分有趣的數學練習,更重要的是可以通過后續預報應用研究,建立起一個更為復雜、完美的數學表達公式,乃至為水文學建立更為科學的理論打下基礎。
洪水來水過程是一個漲水段相對較短、退水段相對較長的時序物理現象。這種形態的過程在其它領域也廣泛存在,如通信的電話流量、公路交通流量過程等等。
由于許多水文物理量與指數函數e-at有密切聯系,那么,由此推測洪水過程線的公式表達應當是以指數函數的初等運算為構成形式。果然,將兩個不同退水系數的指數函數進行相減,就是一條很完美的洪水流量過程線。
Q(t,a,b)=A×(e-at-e-bt) 或
Q(t,a,b)=A×(exp(-at)-exp(-bt))
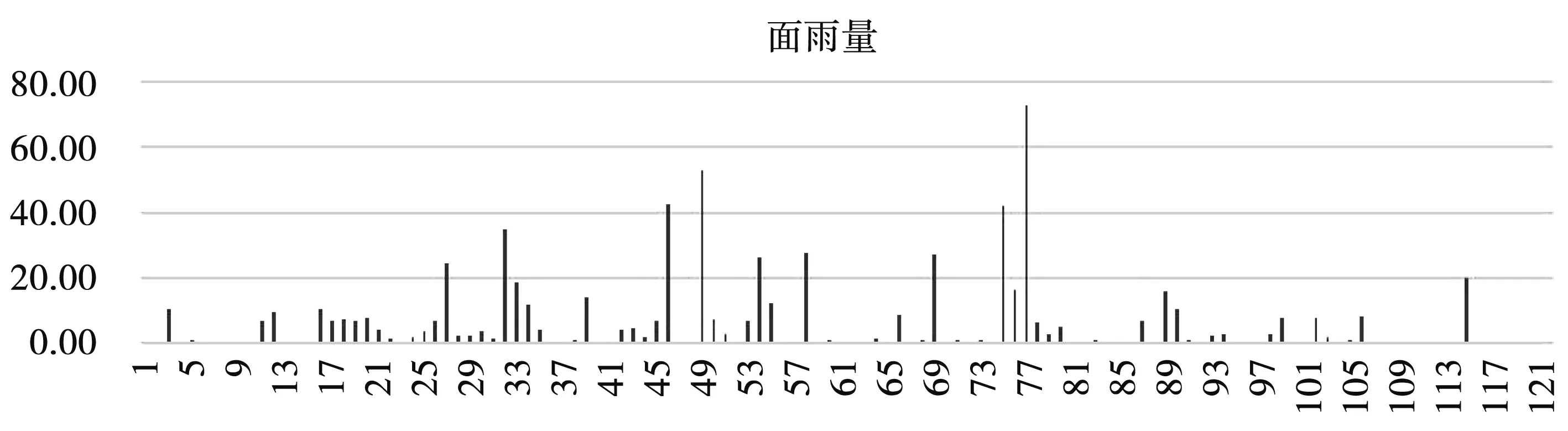
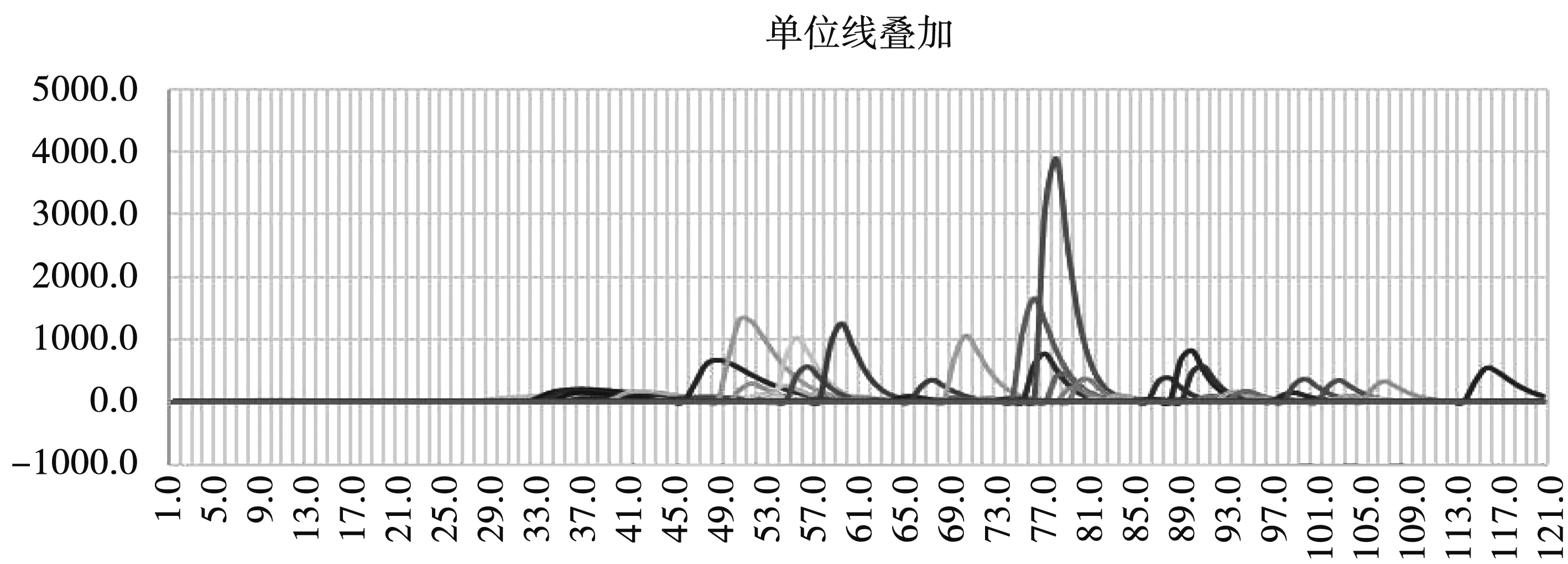
其中a 注:洪水曲線公式Q(t,a,b)=A×(e-at-e-bt) 的積分面積(洪水總量): 發現洪水徑流過程Q-T曲線的數學公式后,工作僅僅是開始,還需要對洪水過程線公式進行數學處理,并解決Q-T曲線族的等分或非等分變化,目的是要讓徑流過程曲線族與實際流域不同干濕條件下的洪水單位線一一匹配,這樣才有可能解決數學公式其代表的完備性與理論外延的合理性,其成果可以視為理論單位線。之所以稱為理論單位線是因為Q-T曲線族的每條曲線的積分面積均為1。 通過反復試錯后,合理選取不同的(a,b)參數,就可以完整地反映所有的洪水過程的變化趨勢。理論單位線曲線族典型曲線見圖2。 圖2 理論單位線曲線族典型曲線 理論單位線曲線公式: Q(t,a,b)=1/(1/a-1/b)×(e-at-e-bt) 峰現時間: Tf=ln(a/b)/(a-b) 洪峰流量: Qf=ab/(b-a)×(e-aln(a/b)/(a-b)-e-bln(a/b)/(a-b)) 每條理論單位線的積分面積(t=0~∞): 每條理論單位線的計算面積(t=0~∞): s=∑Q(t,a,b)<1.0 注:曲線公式Q(t,a,b)=A×(e-at-e-bt)的面積S=A/(1/a-1/b)(A為常數) 基本假定:存在某一組參數(a,b)或(ai,bi)的理論單位線曲線族與徑流系數(產流系數)可以建立唯一的對應關系,即曲線Q1,Q2,Q3,Q4,Q5,Q6,Q7,Q8,Q9,Q10分別對應徑流系數為0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0的洪水過程。基本假定能否符合實際,將通過后續預報應用和試錯方法來檢驗。 給定不同的a,b參數就能得到不同的單位線,只要根據產流條件不同去合理調整a,b參數就能獲得理想的洪水過程線,同時也就完成了相應的洪水徑流匯流預報計算。 建模方式:先給定一組a,b參數的洪水預報標準模型,建立徑流系數與理論單位線族的關系對應表;實際流域預報將根據徑流系數(又稱產流系數、出流系數)找到對應的單位線。同時,計算實際流域洪水歷時與標準洪水歷時的比值作為匯流標尺參數,進而計算時間標尺進行時標變換,代入理論單位線曲線公式即可完成洪水匯流預報計算。 如果預報結果不理想,重新給定另一組a,b參數的洪水預報標準模型,進行預報應用檢驗,直至預報結果完美。 洪水預報標準模型表見表1。 表1 洪水預報標準模型表 用退水段的平均退水系數代表該洪水曲線的退水系數(稱為標準退水系數B標準),并與徑流系數r建立回歸關系。見圖3。 本地退水系數:B本地=B標準^Tc 時間標尺:Tc=BT×DT/24 其中:DT為當地模型計算時段長(小時),匯流標尺BT為實際流域洪水歷時與標準洪水歷時的比值。 退水系數B與徑流系數r關系見表2。 表2 退水系數與徑流系數關系 退水系數僅用于預報模型開始時(預熱段)的前期退水的計算,之后的連續預報則無此需求。 理論單位線曲線參數: ai=0.00875×(ri×Kqqt×10)^2+0.02375×(ri×Kqqt×10)+0.0175 bi=0.00875×(ri×Kqqt×10+1)^2+0.02375*(ri×Kqqt×10+1)+0.0175 si=100×(1/ai-1/bi) 其中:Kqqt各種匯流應用調節系數,用于洪水過程的局部修正(主要由人類活動影響確定)和洪水過程的整體修正(可由洪峰修正系數確定);ri為時段i的徑流系數(又稱產流系數、出流系數),是參數ai,bi的主要控制變量。 單位線匯流時段平均流量(m3/s): qij=0,當tj-ti<1 qij=-Ri/0.000864×100/si×TC×((exp(-ai×(tj-ti)×TC)-exp(-ai×(tj-ti)×TC))/ai/TC-(exp(-bi×(tj-ti)×TC)-exp(-bi×(tj-ti)×TC))/bi/TC),當tj-ti>=1 其中:Ri為時間標尺TC、時段i的產流量(又稱徑流總量),108m3。 理論單位線預報應用實例:將理論單位線曲線族模型應用到豐滿2013年連續洪水預報當中,預報曲線與實際曲線符合程度較高,預報結果見圖4-圖6。 圖4 豐滿流域面雨量 圖5 單位線曲線族疊加曲線 圖6 豐滿2013年連續洪水預報曲線 1) 洪水徑流數學描述——理論單位線曲線族數學公式的提出,為水文基礎理論在匯流方面的研究提供了一種新的完備理論匯流模式。 2) 理論單位線曲線族數學公式及其標準結構設計具備外延遞推的合理性,通過理論單位線曲線族與徑流系數之間建立恰當的關系,可以解決復雜的流域徑流的匯流預報問題。 3) 由于理論單位線族具備豐枯全過程連續覆蓋的洪水匯流計算特性,從而有望與其它高精產流預報模式相結合,為后續建立精確的產-匯一體預報模型提供堅實的理論算法,達到自動選配單位線,實現高精、高效預報的目的。4.2 理論單位線曲線族數學公式
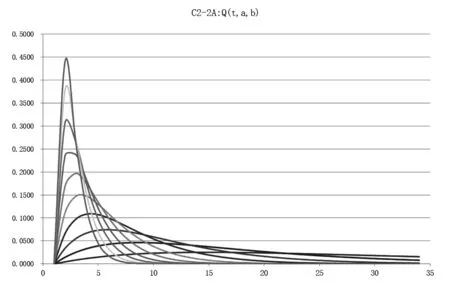
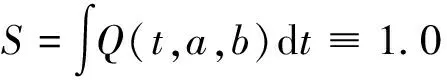
5 理論單位線應用建模(匯流理論模式)
5.1 洪水預報標準模型表(理論單位線族)
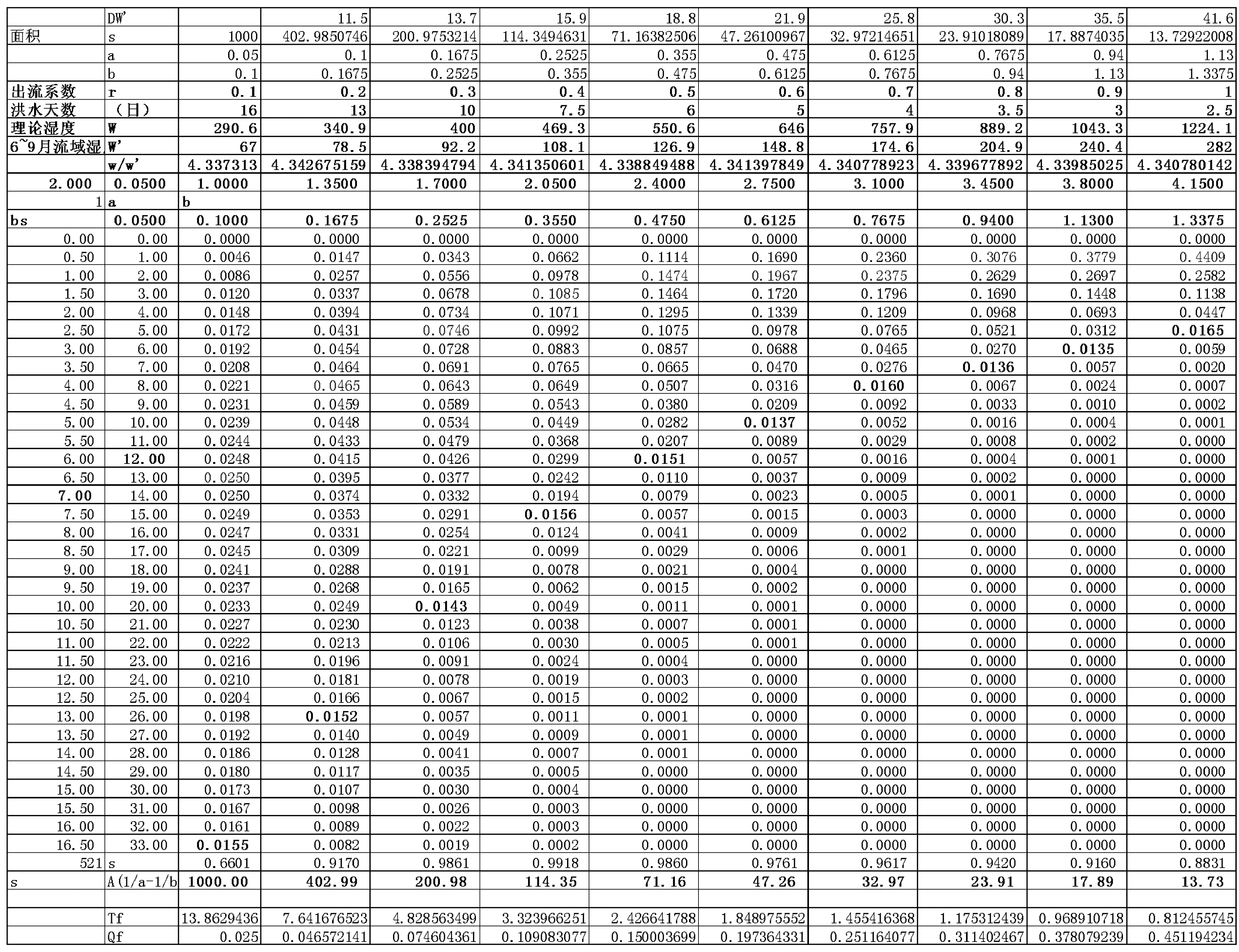
5.2 確定退水系數B和時間標尺Tc

5.3 確定理論單位線參數
5.4 計算單位線匯流時段平均流量

6 結 論

