基于MEMS傳感器組合的行人室內高度定位算法

劉 宇，李 瑤，路永樂，邸 克,郭俊啟，方 針

( 1. 重慶郵電大學 先進傳感器件與系統集成研究室，重慶 400065；2. 中國電子科技集團公司第二十六研究所，重慶 400060)

0 引言

GPS信號在室內被嚴重遮擋，無法利用。目前應用較廣的室內測高技術主要分為兩類：

1) 基于無線局域網、藍牙、射頻識別、超寬帶等基礎設施的測高技術[1-4]。這類技術需要在室內預先部署設備，自主性差。

2) 基于氣壓計的測高技術。氣壓計測高具有自主性好，精度高，實時性強等特點，但易受環境溫度的影響，可靠性較低[5-6]。

慣性導航技術依靠慣性傳感器進行姿態解算，具有良好的自主性[7]。由于氣壓計的優點及局限性，一些學者提出了基于慣性傳感器與氣壓計融合的室內高度算法。Zhu J X提出了一種融合氣壓計數據和加速度計積分得到的高度方差進行上、下樓判定[8]。但微機電系統(MEMS)加速度計精度較低，誤差較大，基于加速度計積分得到的高度會隨時間發散。Zheng L提出了一種基于足部佩戴方式、氣壓計和加速度計融合的高度算法，該算法通過卡爾曼濾波融合氣壓計高度數據和加速度計積分的高度數據進行高度解算，同時利用零速修正算法降低加速度計的高度漂移誤差[9]。零速修正算法雖然可以降低加速度計積分的高度漂移誤差，但僅適用于足部，對腰部設備適用性差。

本文提出了一種基于腰部佩戴方式、加速度計和氣壓計融合的室內高度定位算法。該算法分別利用加速度計的峰值特征和四分位距值特征進行上樓判定和下樓判定；然后利用氣壓計計算行人步高進行高度計算。為了降低環境溫度對氣壓計的影響，本文將濾除氣壓突跳的高度數據，減少高度誤差。經實驗驗證，本文的高度定位算法受環境溫度影響較小，且本文算法高度與實際樓層高度的誤差小于2 m，能夠將人員定位到正確樓層。

1 慣性單元介紹

本文使用的微慣性測量單元集成了三軸MEMS加速度計、三軸MEMS陀螺儀及氣壓計。該慣性單元置于人員的腰部位置，本系統采用的導航坐標系為東、北、天坐標系，簡稱為n系。載體坐標系為b系，x、y、z方向為前、左、上方向。

1.1 步態檢測

根據行人步行的運動特性，行走時加速度計三軸模值輸出波形成周期性變化，因此可利用該周期性來檢測行人步態。三軸加速度模值為

(1)

式中ax、ay、az分別為加速度計三軸輸出的數據。

對anorm進行峰值檢測，一個峰值點(波峰或波谷)記為1步。

1.2 氣壓計解算高度

實際的大氣溫度隨高度的增加而遞減。以平均海平面為起算高度，行人高度和氣壓的關系為

(2)

式中：H為行人的高度；P為觀測點的氣壓值；P0=101 325 Pa為標準氣壓。

根據式(2)可計算得到行人的絕對高度，但在室內，絕對高度無法提供行人的高度位置。因此需要計算2個位置的相對高度，得到行人在室內的高度為

ΔH=H2-H1

(3)

式中：H1為氣壓計測量的行人初始位置高度；H2為氣壓計測量的行人當前時刻位置的高度。本文將行人初始位置高度置為0。

2 融合高度定位算法

為了降低外界環境對氣壓計的影響，本文利用加速度計對人員的上、下樓狀態進行識別，利用濾出了氣壓突跳值的氣壓計數據進行高度解算，本文算法框圖如圖1所示。圖中，h0,h1,h2為本文算法涉及高度的相關參量。

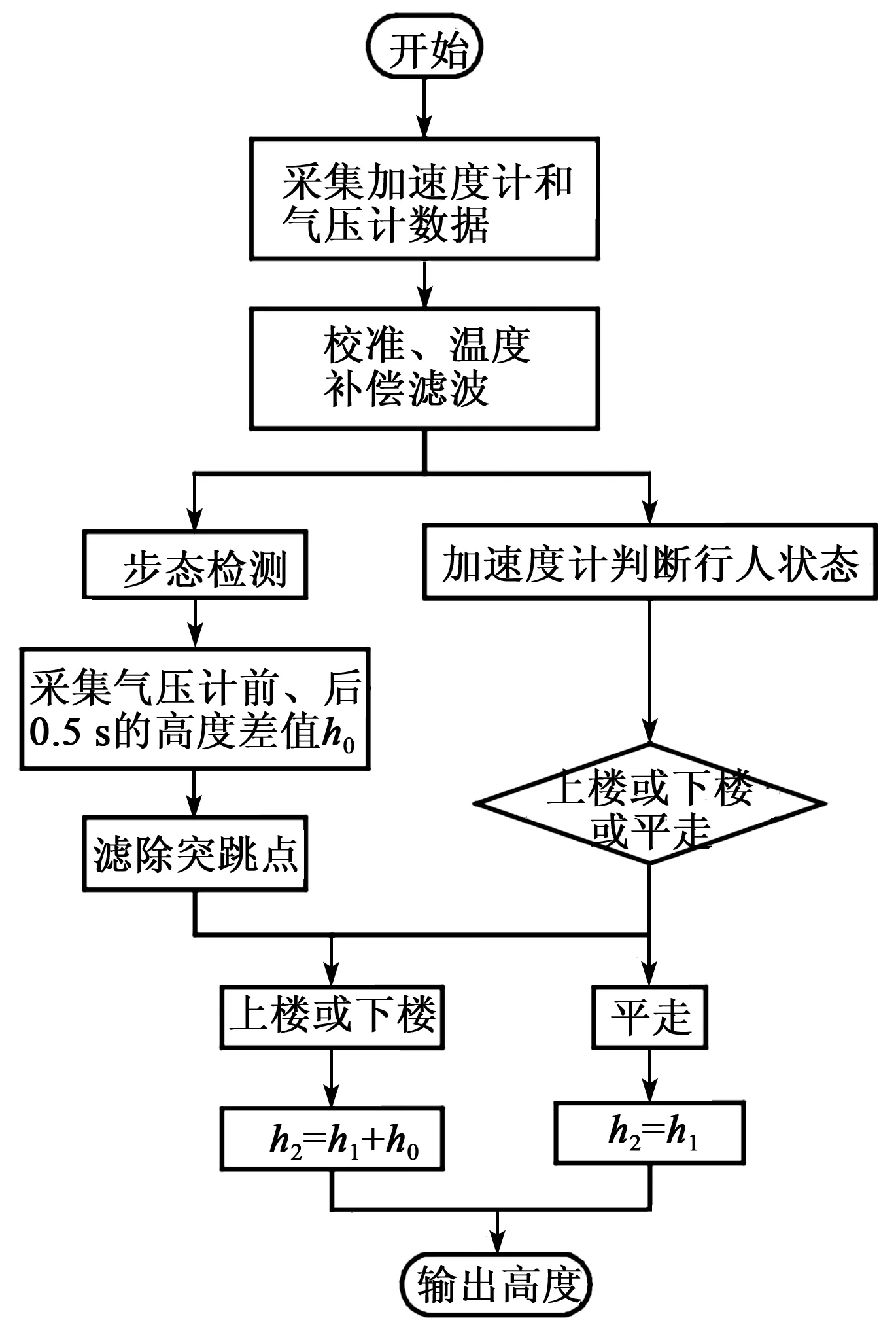
圖1 高度算法框圖

2.1 加速度計判定上下樓

四分位距也稱為四分差，可用來反映一段數據的離散程度。行人在行走過程中，下樓的頻率較平走和上樓的頻率更大，因此，可用四分位距值作為識別上、下樓的參考量。四分位距值為

QIQR=Q3-Q1

(4)

式中：Q1為前50個數據的中位值；Q3為后50個數據的中位值。數列長度選取100，將數列的數據按從大到小排列。

本文采集了行人上、下樓及平走的加速度數據，通過分析加速計的峰值特征及四分位距值特征發現，可利用x軸加速度計的峰值進行上樓識別，利用z軸加速度計的四分位距值特征進行下樓識別，如圖2所示。

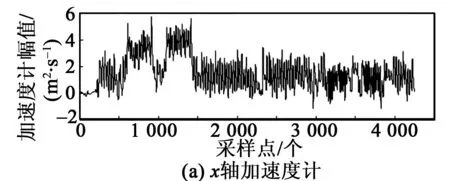
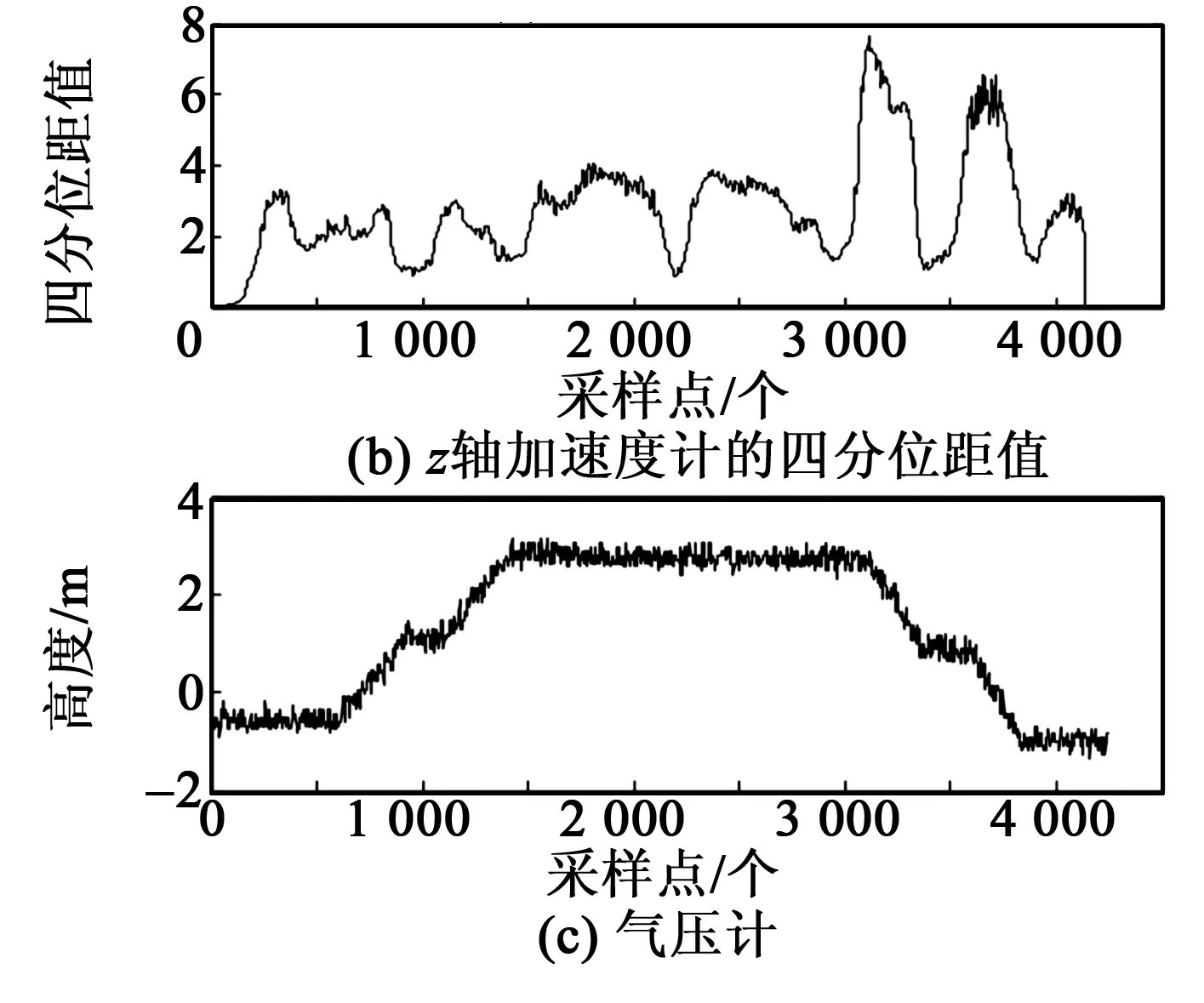
圖2 加速度計的數據特征

利用加速度計的峰值特征和四分位距特征對行人的上、下樓及平走姿態進行識別，上、下樓姿態識別條件為

(5)

式中：Axmax為x軸加速度計的波峰值；avxmax為平走時x軸加速度計的波峰值均值；AzIQR為z軸加速度計數據的四分位距值;avzIQR為平走時z軸加速度計數據的四分位距值均值；α為上樓判定設置的閾值，β為下樓判定設置的閾值。

2.2 改進的氣壓計測高度

當行人在上、下樓受到環境溫度的影響時，氣壓計會產生高度漂移誤差。為了提高氣壓計測高的精度，本文以前、后0.5 s的氣壓高度差值h0作為參考量。當氣壓計受到環境溫度影響時，h0會發生變化，本文將濾除這些氣壓差值h0，不參與高度解算。

本文采集了大量行人在正常環境中上、下樓的氣壓高度差值h0，如圖3所示。同時也采集了行人平走進入環境溫度升高(進入制熱的空調房)和環境溫度降低(進入有冷風的地方)區域的氣壓高度差值h0，如圖4所示。

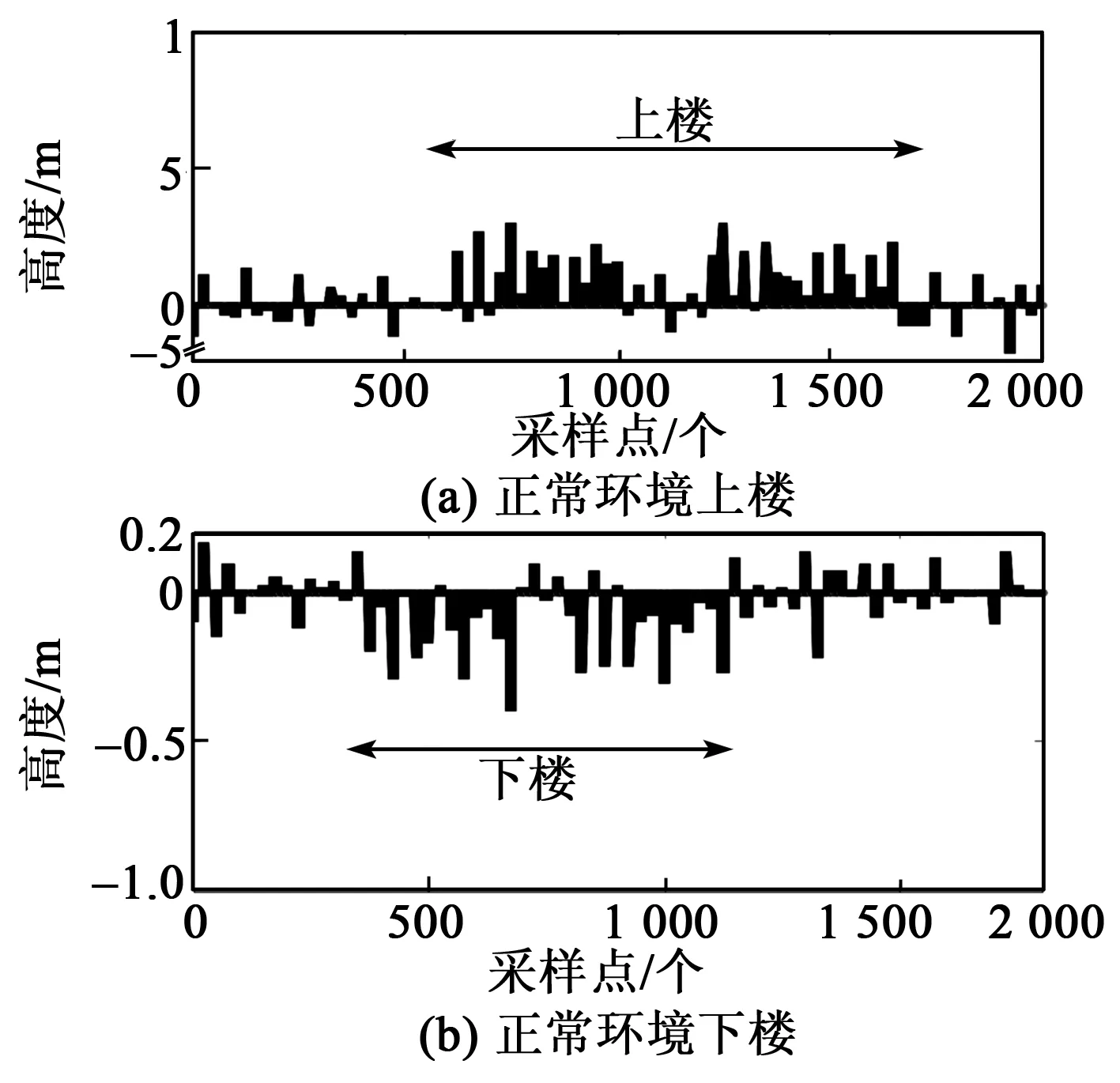
圖3 行人上、下樓時的氣壓差值

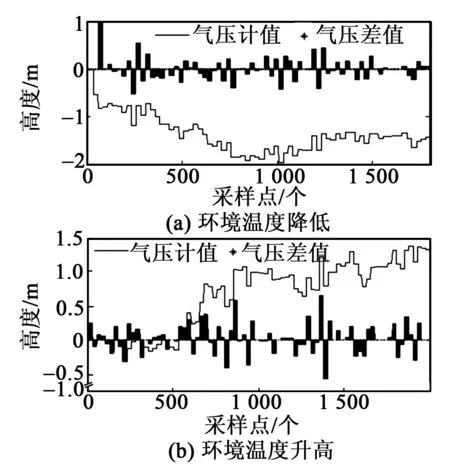
圖4 平走時環境溫度改變的氣壓差值

由圖3、4可看出，行人在正常環境上、下樓時，h0一般為0.1～0.3 m。行人行走過程中氣壓計受溫度影響時，前、后0.5 s內,h0絕對值一般為0.35～0.50 m，甚至高達1 m。

為了降低環境溫度對氣壓計的影響，提高氣壓計測高的精度，本文將濾除“氣壓突跳點”，濾除條件為

|h0|>λ

(6)

式中λ為濾除氣壓突跳點的條件閾值。式(6)成立，則認為該氣壓差值為突跳點。當檢測到氣壓突跳點時，則h0不參與高度計算。

本文的高度計算式為

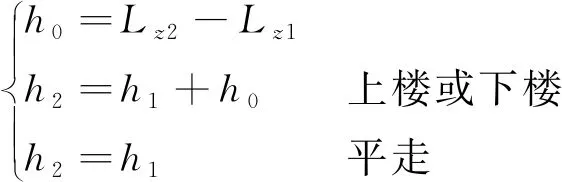
(7)

式中：Lz2為當前時刻氣壓計輸出高度；Lz1為前0.5 s氣壓計輸出高度；h2為當前時刻本文算法解算的行人高度；h1為前一步解算的行人高度。設行人的初始位置高度為0。

為了減少上、下樓誤判造成的高度誤差和氣壓計的高度誤差累積，本文提出了一種改進的高度修正算法：行人平走時都在建筑的半層樓高處或整層樓高處，因此，當檢測到行人平走時，可以將行人高度修正到半層高的整數倍，即

h2=hc×n(平走)

(8)

式中：hc為建筑的半層樓高；n=-2,-1,0,1,2，…等整數。

3 實驗驗證

本文將從兩個方面對本文算法進行驗證:

1) 驗證本文算法不易受環境溫度影響。

2) 驗證本文算法的精度。

第一次實驗設計為：實驗地點為重慶郵電大學第一教學樓，層高4 m。行走路徑為：行人從1樓走到4樓，其中3樓上4樓時，改變環境溫度(用熱水袋放在慣性單元旁邊，使環境溫度升高，如圖A點)，然后再從4樓走到1樓室外(有冷風，如圖B點所示)。高度解算結果如圖5所示。

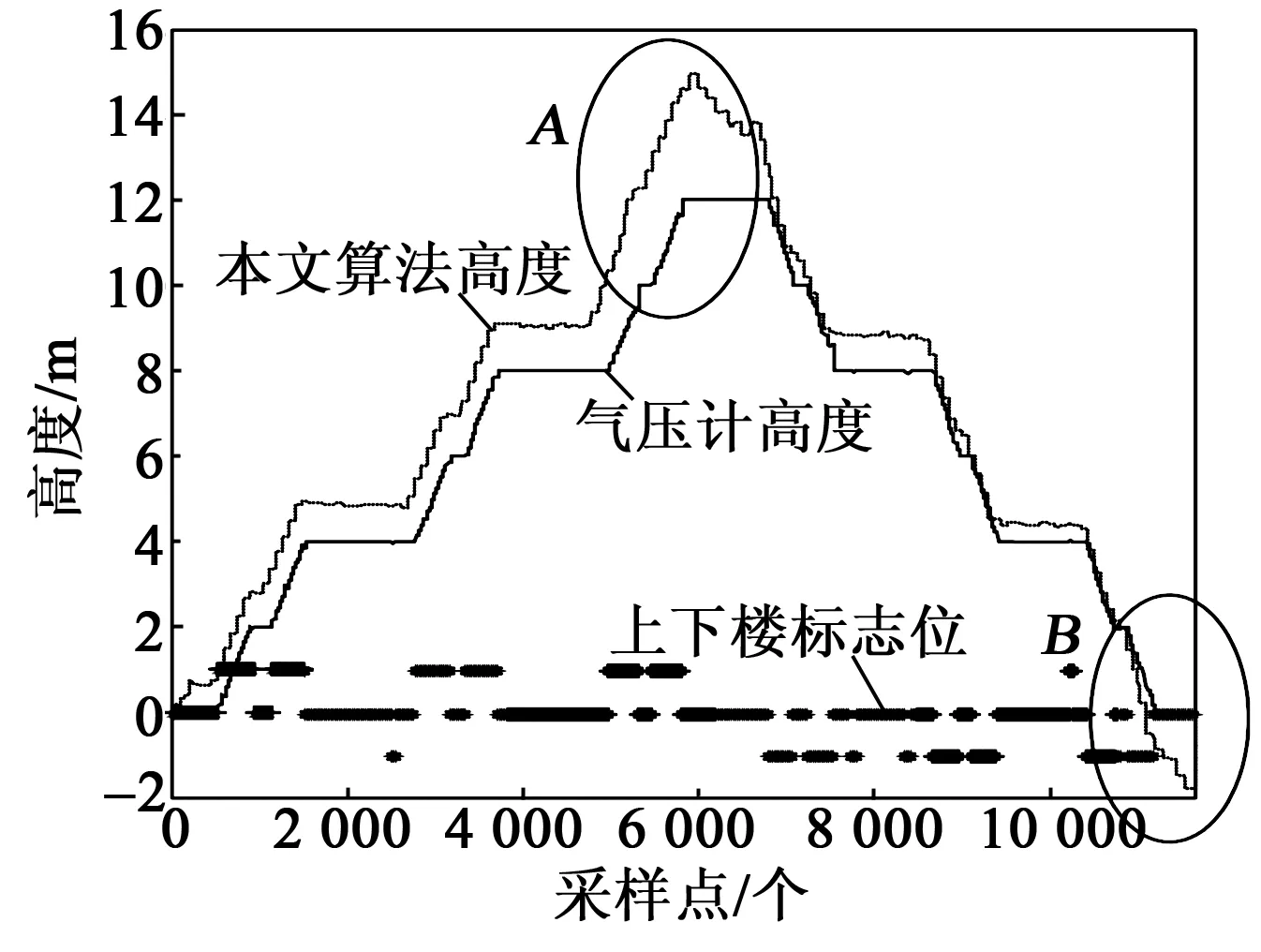
圖5 改變環境溫度的高度對比

由圖5可看出，當改變環境溫度時，基于加速度計的上、下樓識別算法未受影響。行人從3樓上4樓時，由于環境溫度的升高，氣壓計高度增加了約3 m(見圖5中A點)；當行人從1樓走到室外時，由于環境溫度的降低，氣壓原始高度降低了約1.8 m(見圖5中B點)。由于本文高度解算算法濾除了氣壓突跳點，所以,本文算法解算高度并未產生很大的高度誤差。

第二次實驗為驗證本文算法上、下樓識別的準確率，本文選擇了4名不同身高、性別的實驗人員，實驗地點為重慶郵電大學信科大樓。本次實驗設計為：每個實驗人員都從1樓上到4樓，然后平走，最后從4樓下到1樓，行走路徑如圖6所示。經統計，每層樓上樓階梯數和下樓階梯數均為25階，平走過程中，記錄員記錄實驗員的平走步數，實驗結果如表1所示。

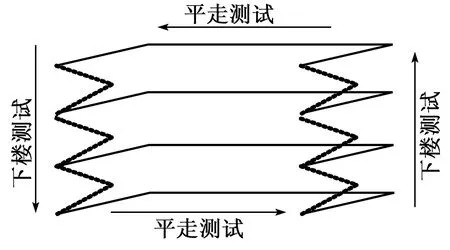
圖6 行走路徑

表1 上、下樓測試結果

由表1可看出，本文算法的上、下樓姿態識別準確率很高，上樓準確率均大于94.6%，下樓準確率均大于97.3%，平走識別率大于98.2%。

第三次實驗為高度精度驗證實驗。本文選擇了4名不同身高、性別的實驗人員。本次實驗設計為：選擇了2個層高分別為4 m、5 m的建筑，實驗人員在從1樓出發，首先經過隨機的上、下樓行動后，到達7樓；然后再經過隨機的上、下樓行動，到達3樓，實驗結果如表2所示。

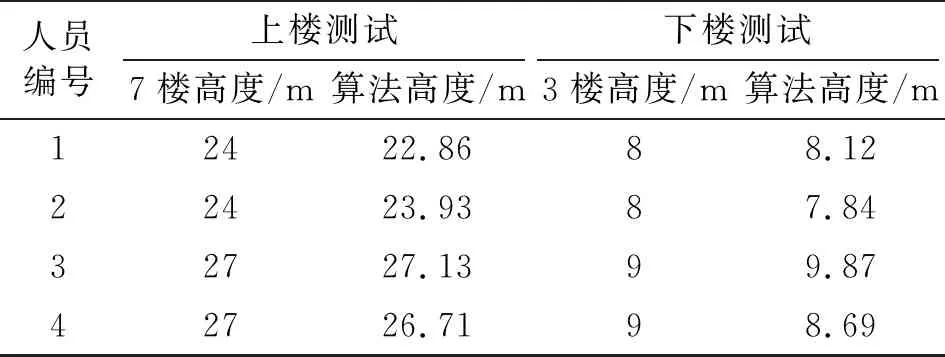
表2 高度測試結果

由表2可看出，不同人員在不同建筑的上、下樓測試中，本文算法解算的高度與樓層實際高度的誤差均小于2 m,而建筑層高一般為4～5 m，所以,本文算法可將人員準確定位到樓層。

4 結束語

針對氣壓計易受環境因素影響的問題，本文提出了一種基于腰部穿戴、加速度計和氣壓計融合的人員室內高度定位算法。經實驗驗證，該算法不易受環境溫度的影響，算法解算高度與實際樓層高度的誤差小于2 m。因此，本文提出的人員室內高度定位算法可有效應用到各種環境變化較復雜的領域，具有很高的工程應用價值。