利用相關系數法確定三種位場垂向導數換算的濾波參數

任朗寧，張鳳旭，郝夢成，李銀飛

吉林大學 地球探測科學與技術學院,長春 130026

0 引言

垂向導數作為常規的位場數據處理方法，不僅在分離疊加異常、突出局部異常和識別地質體邊界等方面具有重要作用[1--3]，還是其他一些位場數據處理方法的重要環節。例如歐拉反褶積、向下延拓[4]和重力歸一化總梯度等方法都需要先進行垂向導數的換算，并且導數換算的結果精度將直接影響到上述位場處理方法的最終計算精度。由于導數換算對噪聲的敏感性，常常得不到較好的求導結果，影響后續異常的處理與解釋。為此，許多改進位場垂向導數換算的方法被提出，它們大致可分為兩類：一是空間域法；二是波數域法。空間域法包括量板法、邊界單元法和樣條函數法等[5--7]。波數域法包括常規FFT法、維納濾波法[8]、補償圓滑濾波法[9]和正則化方法[10]等。

為改善導數換算的不穩定，常規做法是通過引入低通濾波器，將其與垂向導數算子相結合，構建新的垂向導數算子，來壓制垂向導數計算過程中噪聲的放大作用。Butterworth低通濾波、Hanning窗濾波以及向上延拓濾波是3種常見的低通濾波，在導數計算中取得了較好的效果，但各方法的濾波參數常常需要反復嘗試，降低了計算效率，筆者利用相關系數法來選擇合適的濾波參數，實現位場數據3種方法快速垂向導數換算，降低了人為因素對導數結果的影響。

1 方法原理

1.1 垂向導數中常用的低通濾波因子

位場G(x,y)與其各階垂向導數VDm(x,y)(m代表階數)在波數域的關系式為[11]：

(1)

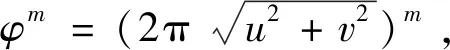
VDm(u,v)=φm·G(u,v)

(2)

由前人研究可知[12]，φm是一個放大型因子，求導過程會對高頻噪聲放大，導致垂向導數結果精度變差。通常的做法是在常規導數因子中附加一個低通濾波器來減小φm在高頻部分的放大作用，保留低頻有效信息。下面給出三種常規的低通濾波方法：

①Butterworth低通濾波器是一個在通帶內擁有最大限度平坦度的濾波器，其頻率響應為：

(3)

式中：ω為頻率；ωb為Butterworth濾波器的截止頻率;N為濾波器階次。

②Hanning窗低通濾波是位場信號處理中常用的一類窗函數濾波因子,其表達式[13]為：

(4)

式中：ωh為Hanning窗濾波器的截止頻率。

③向上延拓是將觀測平面上的異常換算到觀測平面之上，相當于一個低通濾波[14]，在波數域中，向上延拓因子是:

(5)

式中：h是上延高度。

由上述的式(2～5)可各自構造出新的求導公式：

VDB(u,v)=B(ω)·VDm(u,v)

(6)

VDH(u,v)=H(ω)·VDm(u,v)

(7)

VDY(u,v)=Y(h)·VDm(u,v)

(8)

將結果進行Fourier反變換，即得到垂向導數結果。

從上式及前人研究結果可知，這些方法的濾波效果主要與低通濾波器濾波參數(截止頻率或上延高度)的選擇有關。以截止頻率的選擇為例，當截止頻率過小時，求導導致低頻部分的有效異常損失；當截止頻率過大時，求導過程中對噪聲的壓制作用較弱。這兩種情況都會導致導數換算結果的精度不高，因此需要選擇一個合適的截止頻率來平衡這兩種狀況，即在保留有用信號的同時，最大限度的減少噪聲干擾。

1.2 基于相關系數法的濾波參數選取方法

為了快速確定濾波參數，這里借鑒曾華霖確定最佳上延高度時采用的相關系數法[15]。即利用取不同濾波參數時，求導結果之間的相關性來確定最佳濾波參數。具體做法是：

①求原始異常的Fourier變換譜；

②在一定范圍內，設置n個離散的濾波參數，并計算相應的垂向導數；

③利用下列公式計算相鄰兩個濾波參數求導結果的相關系數；

(9)

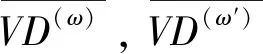
④當相關系數曲線開始趨于穩定的時候所對應的參數確定為最佳濾波參數。

2 模型試驗

為檢驗濾波參數選取的相關系數法在垂向導數計算中的效果， 本文設計包含4個大小埋深各不相同的長方體的組合模型進行試驗。 模型參數見表1。

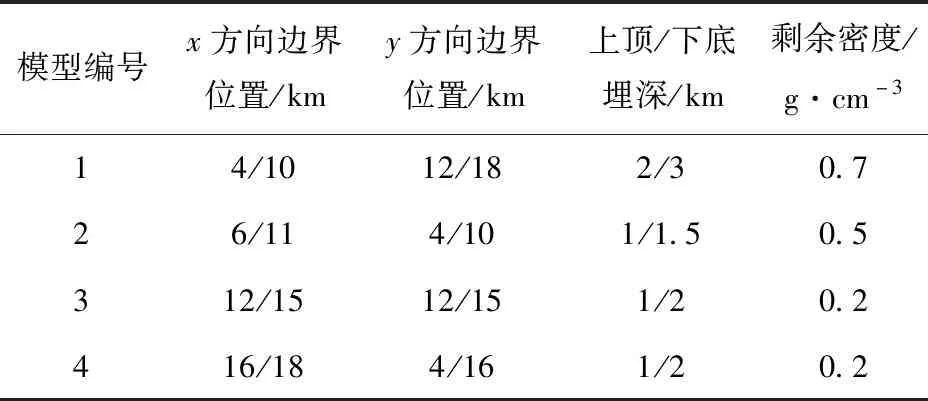
表1 模型參數

在實際中，由于高頻噪聲干擾的始終存在，故對該組合模型產生的重力添加均值為0，標準差為0.1 g.u.的高斯白噪聲，其含噪聲重力異常Δg見圖1a。從圖1a中無法準確識別地質體的真實邊界位置，需要對模型重力異常進行處理。圖1b是該模型的理論垂向二階導數。對比圖1a和圖1b，可以看出異常的垂向二階導數換算，對地質體的異常信息進行突出。

對含噪聲重力異常(圖1a)采用式(6～8)進行垂向二階導數計算。其結果Δgzz見圖1d、圖1f和圖1h。圖1c、圖1e和圖1g分別是Butterworth低通濾波、Hanning窗濾波以及向上延拓濾波進行低垂向二階導數計算的濾波參數選取圖，為驗證相關系數法選取的濾波參數是最佳的，本文還求取了各方法導數計算結果與理論垂向二階導數之間的均方根誤差。從圖1c、圖1e和圖1g中可以看出，Butterworth低通濾波、Hanning窗濾波以及向上延拓濾波的濾波參數分別是ωb=3.413 8，ωh=5.862 0和h=0.206 9，其所在位置與均方根誤差最低的位置相對應，說明利用相關系數法確定濾波參數是合理的。對比圖1d、1f和1h可以看出，經過本文選取合適濾波參數，各方法垂向導數計算中的高頻噪聲均得到了有效壓制，圖1d和1f中的結果相較于圖1h中的處理結果更好，能夠準確地看出異常體的位置和形態，與圖1b中的結果相似。圖1d和1f中的導數結果雖然都能夠較好顯出異常體的位置和形態，但是圖1d異常的幅值與理論值(圖1b)的差距較小，結果精度較高。

為了進一步檢驗各方法的垂向二階導數效果，對導數結果進行二次積分反算，并將積分結果與原異常求殘差，其結果分別見圖2a、2c、2e和圖2b、2d、2f。對比圖2a、2c、2e和圖1a，可以看出圖2a中Butterworth低通濾波的二次積分結果與原異常最相近。再對比圖2b、2d、2f，可以看出圖2b中的殘差結果里包含的地質體異常信息最少，而Hanning窗濾波和向上延拓處理的結果中異常信息較多，說明這兩種方法在垂向二階導數計算中對異常的轉換不夠徹底。綜上所述，使用相關系數法選取最佳的濾波參數的做法是合適的，利用確定的濾波參數獲得垂向二階導數結果中，Butterworth濾波的導數精度最高。

3 實際應用

為了檢驗上述方法在實際數據處理中的效果，對位于大興安嶺外圍的松遼盆地鎮賚地區的布格重力異常數據(圖4a)進行了垂向二階導數計算。數據網格點距0.5 km，網格點數124×231。首先，利用相關系數法選取本文各方法最佳的濾波參數分別為ωb=0.9，ωh=0.9，h=1.8(圖3a、3b、3c)。再將選取的濾波參數代入到各個濾波器中進行垂向二階導數計算，結果見圖4b、4c、4d。對比上述結果可以看出，Butterworth低通濾波的垂向二階導數(圖4b)處理效果較好， 其異常曲線圓滑，對噪聲的壓制作用較好，同時對淺部異常的突出作用也較強；Hanning窗濾波的垂向二階導數結果(圖4c)精度較差，淺部異常較寬緩，說明相鄰異常的分離不夠徹底。而向上延拓濾波的垂向二階導數(圖4d)雖然突出了大部分的淺部異常特征，但是異常曲線明顯存在畸變現象，說明噪聲干擾被壓制的不夠徹底。為了進一步檢驗求導結果的準確性，對各方法垂向二階導數結果求取二次積分并與原異常做差，結果分別見圖5a、5c、5e和圖5b、5d、5f。二次積分的結果與該區原異常進行對比，可以看出Butterworth低通濾波的結果(圖5a)與原異常形態相似，幅值相近，而其他兩種方法的異常形態與原異常存在較大差異，幅值也有不同。從圖5b、5d、5f的殘差結果中可看出，圖5b中的異常特征最少，幅值最低，說明Butterworth低通濾波求取垂向二階導數過程中異常轉換地較為徹底，間接證明了其垂向二階導數的計算結果比其他兩種方法的結果精度高，這與模型試驗的效果相似。

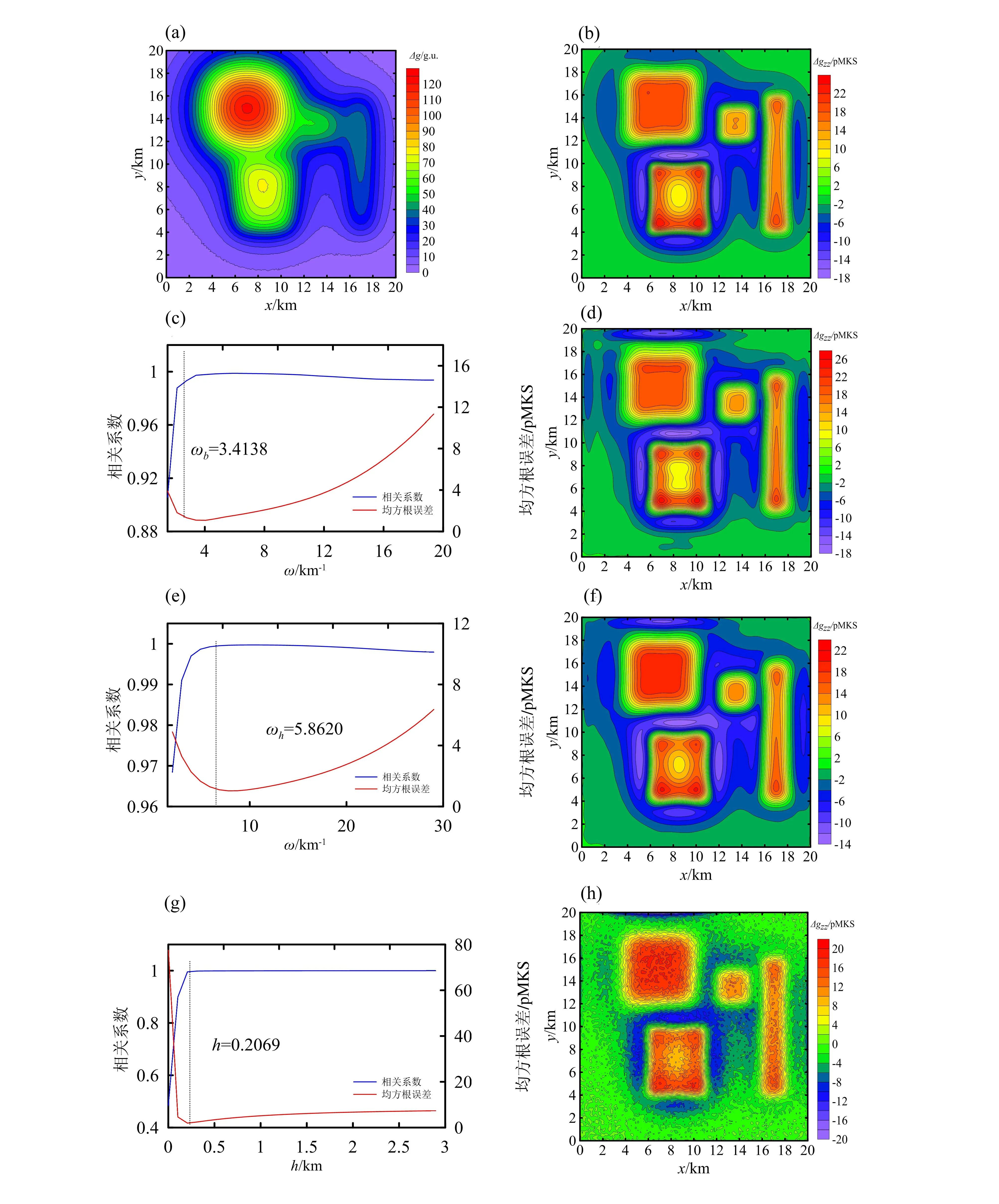
(a)含噪聲重力異常；(b)理論垂向二階導數；(c)Butterworth濾波參數選擇；(d)垂向二階導數(Butterworth濾波器)；(e)Hanning窗濾波參數選擇；(f)垂向二階導數(Hanning窗濾波)；(g)向上延拓濾波參數選擇；(h)垂向二階導數(向上延拓)。圖1 模型重力異常及各方法截止頻率處理效果對比分析圖Fig.1 Comparative analysis of model gravity anomaly and processing effect of cutoff frequency of each method

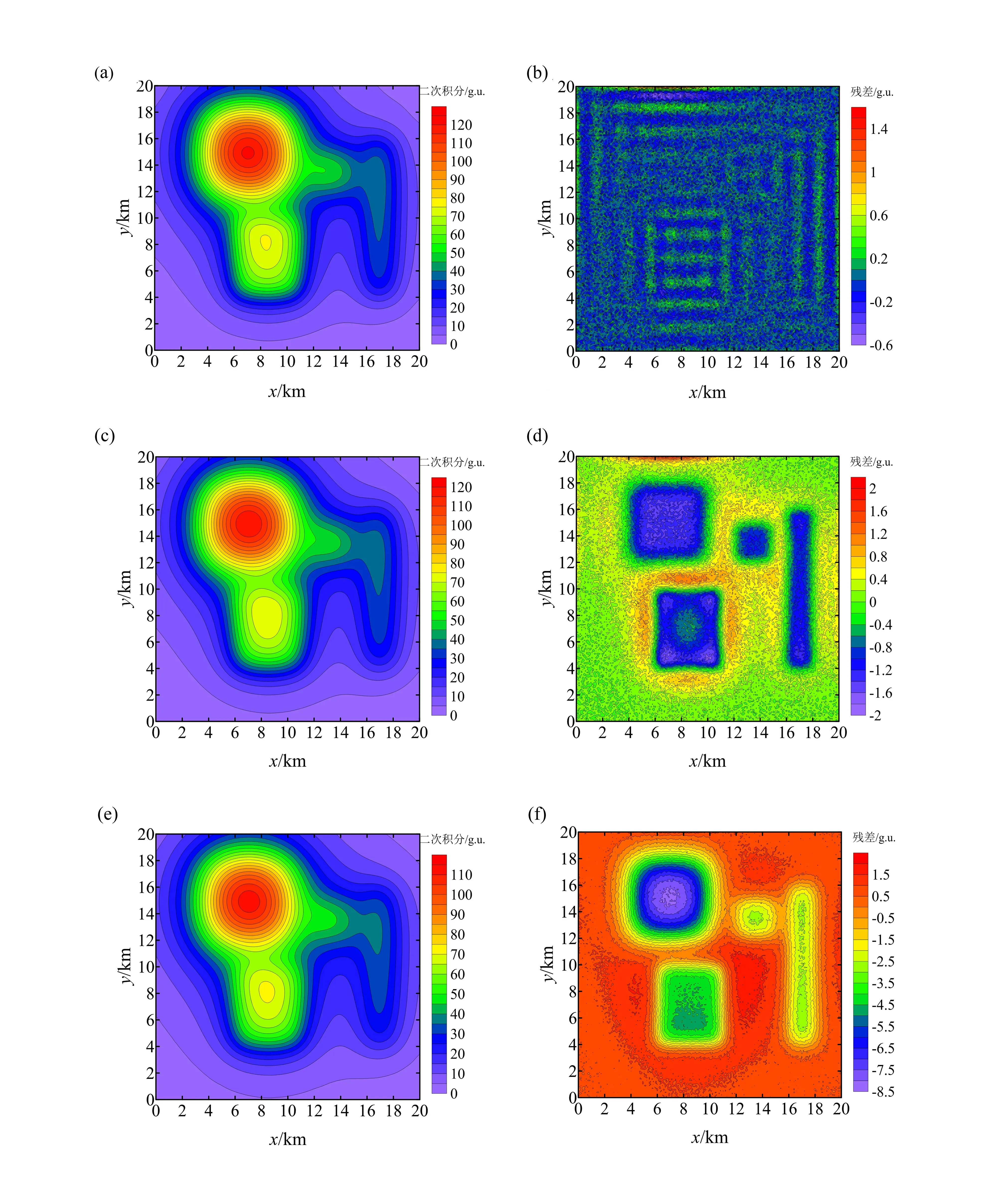
(a)Butterworth二次積分結果；(b)二次積分與原異常殘差(Butterworth濾波器)；(c)Hanning窗濾波二次積分結果；(d)二次積分與原異常殘差(Hanning窗濾波)；(e)向上延拓二次積分結果；(f)二次積分與原異常殘差(向上延拓)。圖2 各方法求導結果二次積分及殘差圖Fig.2 Secondary integration and residual plot of each method

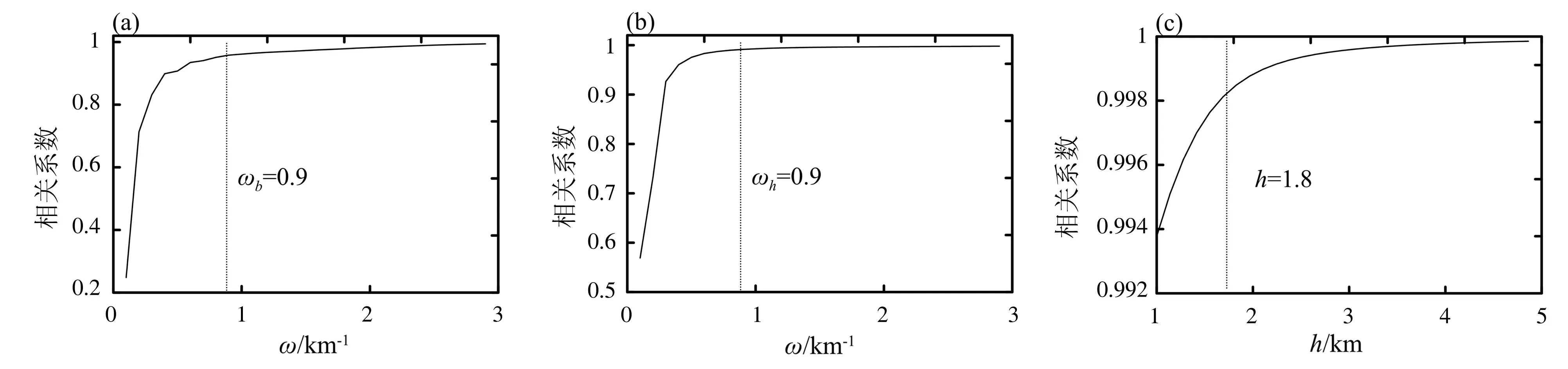
(a)Butterworth截止頻率選取；(b)Hanning窗截止頻率選取；(c)向上延拓上延高度選取。圖3 松遼盆地鎮賚地區各方法截止頻率選取圖Fig.3 Selection chart of cutoff frequency for each method of Zhenlai area, Songliao Basin

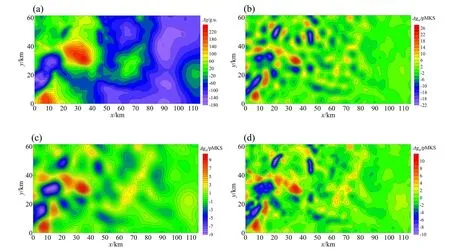
(a)西部斜坡布格重力異常；(b)Butterworth濾波器垂向二階導數；(c)Hanning窗濾波垂向二階導數;(d)向上延拓濾波器垂向二階導數。圖4 松遼盆地鎮賚地區重力異常及垂向導數處理圖Fig.4 Gravity anomaly and vertical derivatives processing map in Zhenlai area, Songliao Basin

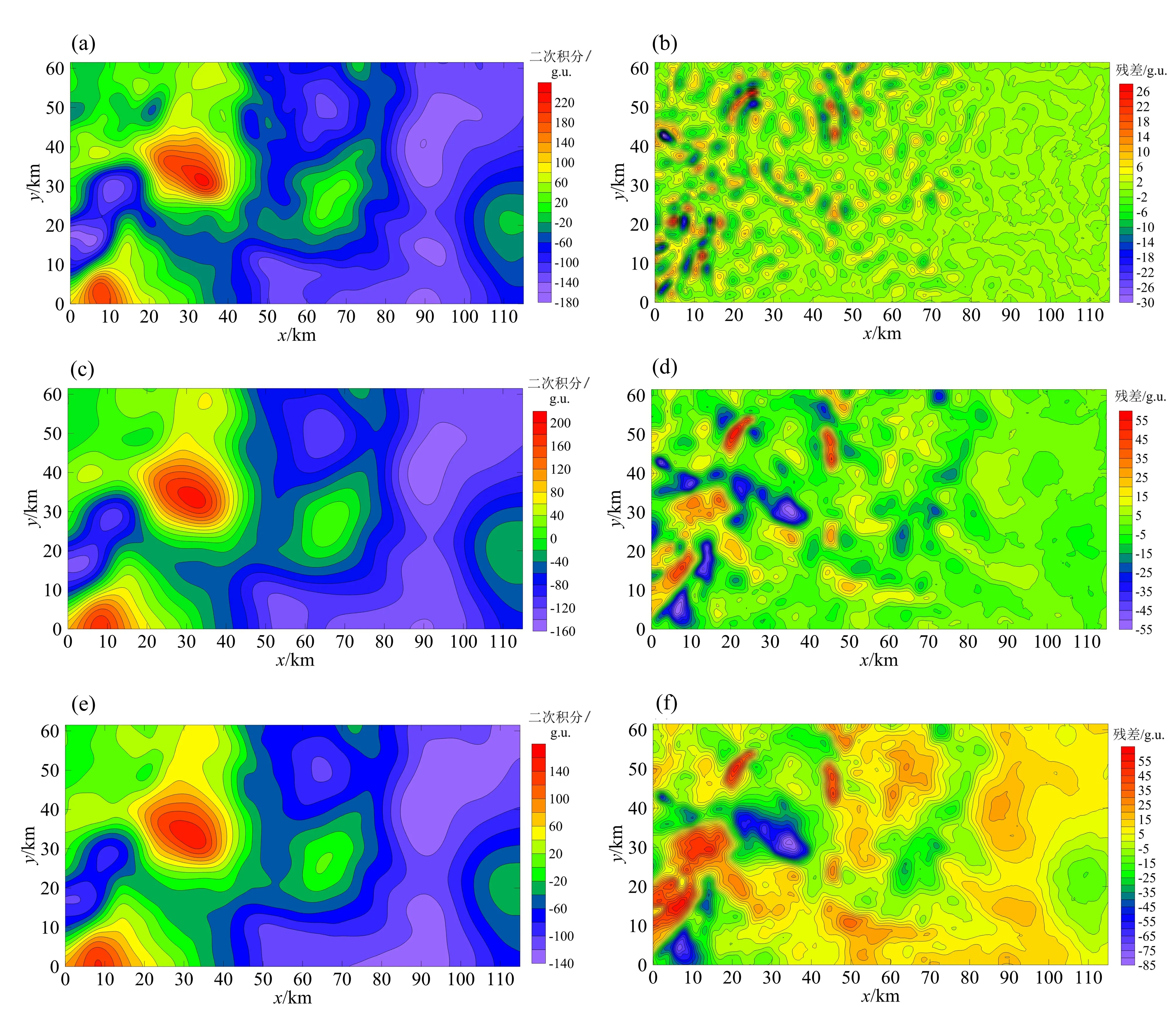
(a)Butterworth二次積分結果；(b)二次積分與原異常殘差(Butterworth濾波器)；(c)Hanning窗濾波二次積分結果；(d)二次積分與原異常殘差(Hanning窗濾波)；(e)向上延拓二次積分結果；(f)二次積分與原異常殘差(向上延拓)。圖5 松遼盆地鎮賚地區各方法求導結果二次積分及殘差圖Fig.5 Secondary integration and residual map of results of Zhenlai area, Songliao Basin

4 結論

(1)使用相關系數法確定了Butterworth低通濾波、Hanning窗濾波和向上延拓濾波的最佳濾波參數，實現了3種方法位場數據垂向導數的快速計算，降低了人為因素對計算結果的影響。

(2)模型試驗結果表明，使用相關系數法選取最佳的濾波參數的做法是合理的，利用確定的濾波參數計算得到的垂向二階導數結果中，Butterworth低通濾波法的導數結果與其他兩種方法的結果相比，精度較高。

(3)松遼盆地鎮賚地區的實測布格重力異常數據處理檢驗了3種垂向導數換算方法的實際效果，獲得了與模型試驗相似的效果，為進一步數據處理與解釋提供了支持。