電池荷電狀態估算方法研究

劉鵬飛

（南京普天大唐信息電子有限公司，南京 210000）

主題詞：電池 電路等效模型 荷電狀態（SOC） SOC估算

縮略語

SOC State Of Charge（荷電狀態）

BMS Battery Management System（電池管理系統）

OCV Open Circuit Voltage（開路電壓）

SEI Solid Electrolyte Interface（固體電解質界面膜）

PNGV Partnership for a New Generation of Vehicles

RC Resistance-Capacitance(電阻-電容)

GNLGeneral Nonlinear Model（非線性等效模型）

ACMAmphiphilic carbonaceous Material（兩親性炭材料）

KF Kalman Filtering（卡爾曼濾波）

EKF Extended Kalman Filter（擴展卡爾曼濾波法）

UKF Unscented Kalman Filter（無損卡爾曼濾波法）

HPSO Hybrid Particle Swarm Optimization（混合粒子群）

BP Back Propagation（神經網絡）

PF Particle Filter（粒子濾波）

LMLevenberg-Marquardt（列文伯格-馬奎特）

GA Genetic Algorithm（遺傳算法）

ADAnalog-to-Digital（模擬量轉數字量）

0 引言

在目前提倡低碳環保健康生活的發展形勢下，以鋰電池為動力的新能源汽車以環保、節能和輕便等優勢正在取代燃油汽車的地位。其使用性能的優劣直接影響到汽車在市場的占有率。電池管理系統（Battery Management System，BMS）作為鋰電池系統中的核心部件，能夠提高鋰電池的安全性和使用年限從而延長鋰電池的使用年限[1]。準確估算鋰電池荷電狀態（State Of Charge，SOC）是BMS的基礎[2]，其估算的準確性有利于BMS對電池的管理和均衡，關系到電池的充放電控制和電動汽車的優化管理[3]。而電池的SOC、電池的開路電壓（Open Circuit Voltage，OCV）、電池端電壓、充放電過程的電流值、電池溫度和電池內阻等參數之間存在關系[4]，因此為了準確估算電池荷電狀態，就需要確定電池荷電狀態與上述參數之間的關系，所有需要建立以電壓、電流、溫度和內阻為主的電池等效模型，從而描述清楚電池的工作過程。本文介紹了目前主流的電池等效電路模型和估算SOC的方法。介紹了各自的原理，分析了各種估算方法間的優缺點，并總結出未來SOC估算的發展趨勢，為新能源汽車發展提供參考。

1 SOC定義

電池荷電狀態（SOC）是電池剩余容量與其充滿狀態時容量的比值，美國先進電池聯合會在《電動汽車電池試驗手冊》中將SOC定義為：在環境溫度為25℃的條件下，電池在一定的放電倍率下，剩余電量與相同條件下額定容量的比值[5]：

其中：Qs為電池剩余容量；Qz為電池額定容量。

2 電池等效電路模型

根據研究方向的區別，用于表征電池狀態的模型也各不相同，可分為電池熱模型、電學特性模型和電池老化模型[6]。通過建立電池熱模型，可以用來預測電池工作過程中內部溫度的變化過程[7]。現在學者在BERNARDI的生熱速率模型[8]的基礎上，研究了電池熱量的來源[9]、電池內部熱量的分布[10-11]、電池內部熱量和電流密度分布[12]、電池組內部熱量傳導[13]等方面的內容，闡明了電池熱量產生的機理以及溫度分布，有助于設計合理的散熱方式來保證電池正常工作。電學特性模型分為可分為黑箱模型、電化學機理模型和等效電路模型。黑箱模型利用神經網絡模型[14]等新型模型結構，建立電池荷電狀態（SOC）、電流、溫度、內阻、開路電壓以及電池端電壓之間的模型，電化學機理模型以NEWMAN提出的多孔電極和濃溶液理論[15-16]來描述電池內部鋰離子濃度和電化學反應變化。等效電路模型通過利用電阻、電容等元件來等效電池電化學反應過程，模型直觀、易懂，結合多種算法可得到較高的準確性，因此具備較強的實用性。目前等效電路模型可分為Rint模型、Thevenin模型、PNGV模型、二階RC模型和GNL模型[17]。電池老化模型主要研究固體電解質界面膜（Solid electrolyte interface，SEI）增長[18]和負極鋰的沉積[19]對電池老化的影響，研究電池老化模型可開發出性能更優的電池材料、延長電池使用年限。

2.1 Rint模型

Rint模型[20]是將鋰電池等效為理想電壓源和電阻串聯的模型，用理想電壓源等效為電池的開路電壓，用常值電阻來等效電池的歐姆電阻和極化電阻。該模型是理想化的模型，未考慮到溫度、荷電狀態、電池老化等外界參數對電池性能的影響，因此此模型多于理想狀態下電池仿真，為高階等效電路模型的建立提供理論依據，并不用于實際SOC的估算[21]。

2.2 Thevenin模型

Thevenin模型考慮到電池工作過程中的極化反應[22]，在Rint模型的基礎上串聯上由傳荷阻抗Re和傳荷電容Ce并聯而成的RC回路[23]，如圖1所示，其中Uoc是理想電壓源，等效為電池的開路電壓；Ro等效為電池的歐姆電阻，因此其端電壓如式（2）所示：其中：U為電池端電壓；UOC為電池開路電壓；I()t為充放電電流；Ro為電池的等效歐姆電阻；Ue為電化學極化電壓。

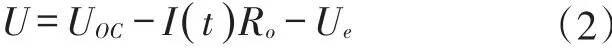
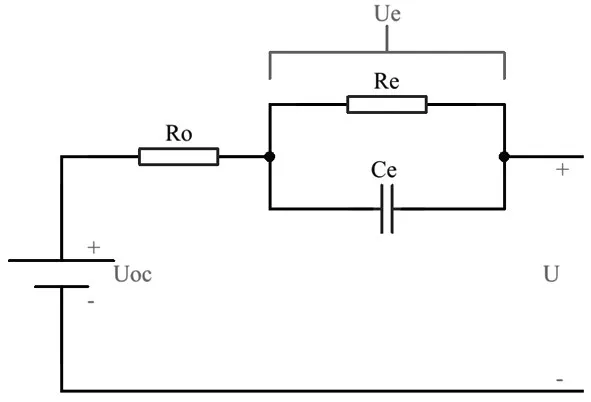
圖1 Thevenin模型電路結構[23]

在Rint模型的基礎上，Thevenin模型不僅考慮到電池工作過程中出現的歐姆極化，同時考慮到電化學極化過程。Thevenin模型結構簡單，元器件具有物理意義，在電池不發生較大變化時，可較為準確的反應出鋰電池在充放電過程中的變化情況。但是隨著電池溫度、電池充放電循環次數的增加、充放電電流等外界因素的變化，模型中電阻值也會發生相應變化，導致模型的仿真精度下降。

2.3PNGV模型

PNGV模型最早由Johnson在《PNGV電池試驗手冊》[24]中提出，考慮到電池的開路電壓隨電流的時間累積的差異，PNGV模型在Thevenin模型的基礎上串聯了儲能電容Cq用來表征電池開路電壓的變化情況。如圖2所示，Uoc是等效為電池的開路電壓；Ro等效為電池的歐姆電阻，Re為傳荷阻抗，Ce為傳荷電容，因此其端電壓如式（3）所示：

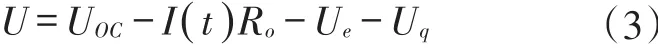
其中：U為電池端電壓；UOC為電池開路電壓為充放電電流；Ro為電池的等效歐姆電阻；Ue為電化學極化電壓；Uq為儲能電容Cq兩端電壓。

PNGV模型利用儲能電容Cq來表征電池開路電壓隨電流時間積分的差異，因此PNGV模型比Thevenin模型具有更高的精確度和動態特性，能更好描述電池充放電過程，但是長時間的充放電過程會在儲能電容Cq累積誤差，從而削減了模型的精確度。

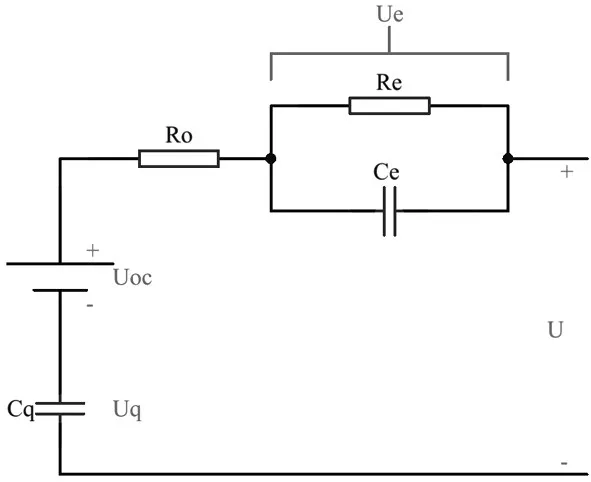
圖2 PNGV模型電路結構[24]

2.4 二階RC模型

二階RC模型[25]是在Thevenin模型的基礎上改進而來的，二階RC模型將電池極化反應分為了電化學極化與濃差極化，因此二階RC模型在Thevenin模型電路上串聯了個用來描述電池濃差極化的RC并聯電路。如圖3所示，其中Uoc是等效為電池的開路電壓；Ro等效為電池的歐姆電阻，Re為傳荷阻抗，Ce為傳荷電容，Rc為濃差阻抗，Cc為濃差電容，因此其端電壓如式（4）所示：

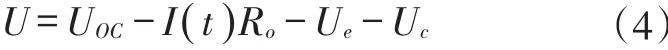
其中：U為電池端電壓；UOC為電池開路電壓為充放電電流；Ro為電池的等效歐姆電阻；Ue為電化學極化電壓；Uc為濃差極化電壓。

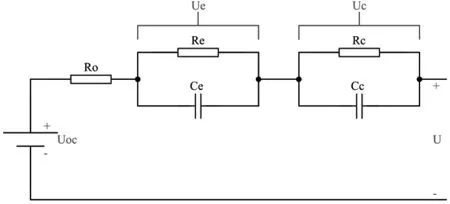
圖3 二階RC模型電路結構[25]

雖然較Rint模型、Thevenin模型而言，二階RC模型電路結構較為復雜，但是二階RC模型同時考慮到電池工作過程中出現的歐姆極化、電化學極化和濃差極化現象，也接近電池的實際工作過程，精度更高，且隨著芯片計算功能的提高，二階RC模型被廣泛用于實際SOC估算中。

2.5GNL模型

GNL模型[26]在二階RC模型的基礎上做出了進一步的優化，電路結構如圖4所示，Uoc是等效為電池的開路電壓；Ro等效為電池的歐姆電阻，Re為傳荷阻抗，Ce為傳荷電容，Rc為濃差阻抗，Cc為濃差電容，Rs為電池的自放電電阻，用來描述電場自放電對電池端電壓的影響，因此其端電壓如式（5）所示：

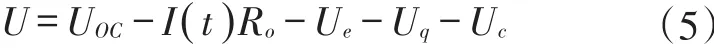
其中：U為電池端電壓；UOC為電池開路電壓；為充放電電流；Ro為電池的等效歐姆電阻；Ue為電化學極化電壓；Uq為儲能電容Cq兩端電壓；Uc為濃差極化電壓。

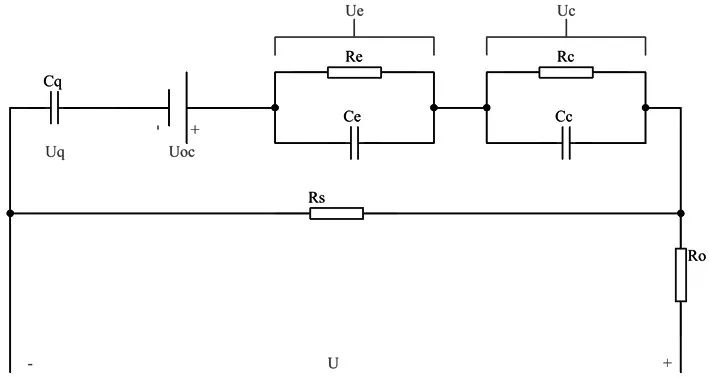
圖4 GNL模型電路結構[26]

GNL模型繼承了上述4種電池等效電路模型的優點，考慮到電池工作過程中各種因素對電池端電壓的影響，因此GNL模型最為接近電池內部特性，因此GNL模型廣泛應用于電池理論分析領域，但是GNL模型階次較高且模型中參數辨識過程較為繁瑣，所以GNL模型并不適用于實際SOC估算中。

3 SOC估算方法

3.1 傳統SOC估算方法

3.1.1 放電法

放電法是公認的較為可靠的估算SOC的方法，適用于所有鋰電池。放電法是指對鋰電池以恒定不變的電流進行長時間的放電，直至將電池放空，放電時間和放電電流的乘積即為電池的放電容量。但該方法一般用于電池容量的標定，測量過程需要離線測試。

3.1.2 開路電壓法

開路電壓法是將電池長時間靜置，使其處于既不放電也不充電的狀態，當電池端電壓不在發生波動時，即為所需的開路電壓，根據建立的開路電壓和SOC關系曲線，通過查詢曲線得到當前開路電壓所對應的SOC。文獻[27]通過對車用ACM電池在不同環境溫度下荷電狀態與開路電壓的關系研究，發現ACM電池在其規定的工作溫度范圍內，其SOC與OCV有著良好的線性關系。

但是直接使用開路電壓法測量電池的荷電狀態時通常需要將電池擱置2 h以上，因此會在測量開路電壓上耗費較多時間。文獻[28-31]采用等效電池模型，通過對電池充放電過程進行試驗，找到充放電過程中電池端電壓與電池開路電壓中間的關系，利用電池端電壓來表征電池的開路電壓，從而來估算電池SOC，以此解決開路電壓法中需要長時間靜置電池的弊端。但是當電池剩余容量為額定容量的30%到80%時，鋰電池的開路電壓基本保持不變，這意味著較小的電壓變化會引起較大的SOC誤差，要追求高精度的SOC估算，對電壓采樣電路精度提出較高的要求[32-33]。

3.1.3 安時積分法

安時積分法[34-35]是利用電池流入流出的電流對時間的積分，計算出電池的輸入輸出電量。安時積分法只與充放電過程中電流值有關，易于實現實時監測，適用于各種電池。安時積分法計算公式如下[36]：

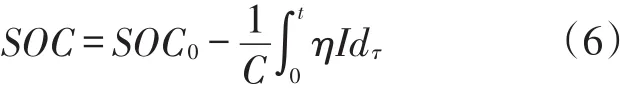
其中：SOC0為電池的初始容量；C為電池的額定容量；I為電池電池，其正負與電池所處狀態有關；η為庫侖效率系數。

因此，電池的初始容量的正確性直接影響到SOC估算結果，因此現有學者[37-38]多采用開路電壓法來估算電池的初始容量，結合安時積分法來估算SOC。電流采樣的誤差會導致SOC的估算誤差，因此往往選用采用精度高的電流傳感來提高電流的采樣精度，但此措施會額外增加系統的成本不易于推廣。學術界在此方法基礎上提出了改進措施，文獻[39]研究了普通傳感器在估算鎳氫電池SOC時產生的誤差，修正了電流傳感器模型，結果表明，利用修正后電池傳感器模型估算電池荷電狀態產生的誤差遠小于修正前的誤差。文獻[40]考慮到溫度、放電電流、充放電次數等因素對SOC估算的影響，提出了一種改進的安時積分法：

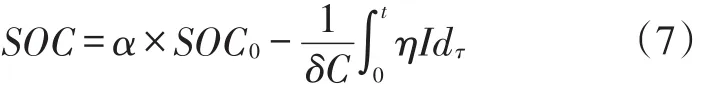
式中，α為自放電及老化因素的修正因子；δ為電池總容量C的修正因子。

3.1.4 內阻法

和開路電壓法一樣，內阻法也是通過大量的試驗測量得到電池的SOC和內阻的曲線圖，SOC的精度，測量時需要將測試電路與電池可靠連接，以減少接觸電阻對SOC估算的影響。直流內阻測試結果不受充電器紋波和噪聲的影響，測量可控制在0.1%之內，但電流過大、時間過長時，電池會出現極化內阻從而增大測量誤差[41]。文獻[42]改進了傳統內阻法，對SOC和內阻變化量ΔR進行建模，結果表明該經驗公式可運用于不同型號的、健康狀況良好的蓄電池SOC測量，測量誤差可控制在10%以內。交流內阻法是在電池兩端加上特定頻率的交流信號，根據測量所得的參數，計算出此時電阻的內阻[43-44]。

3.2 新型SOC估算方法

3.2.1 卡爾曼濾波法

卡爾曼濾波法（Kalman Filtering，KF）采用了噪聲與信號的狀態空間模型。利用前一時刻的估計值和當前時刻的觀測值來更新對狀態變量的估計[45]。估算SOC時，將充放電過程中電流值作為輸入，電池端電壓作為輸出，以電池電壓的實測值和SOC估算值的誤差更新系統的狀態，直至方差最小，得到SOC估算值[46]。該方法的實質是用測量所得的電壓值修正安時積分法得到SOC估算值，其計算方法為[47]：

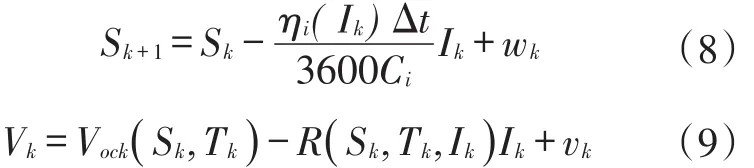
其中：S為狀態變量SOC；I為電流；V為電壓；ηi為電流效率；Ci為電池額定容量；Δt為時間間隔；wk和vk為互不相關的零均值高斯白噪聲。

目前，卡爾曼濾波算法分為標準卡爾曼濾波法（KF）、擴展卡爾曼濾波法（EKF）和無損卡爾曼濾波法（UKF）。文獻[48]比較了KF和EKF估算電池荷電狀態的實驗結果，實驗表明：KF不能降低非線性信號處理存在的誤差，而EKF在估算SOC時能夠將誤差控制在5%以內。文獻[49]在EKF的基礎上，提出了基于模糊控制的EKF的SOC估算法，其可以提高SOC估計精度、減小估算誤差。文獻[50]以電池復合模型為基礎，應用遞推最小二乘法辨識電池參數，利用改進型UKF算法對電池SOC進行估計，改進型UKF算法具有很好的魯棒性和跟蹤速度，各類誤差精度均控制在5%以內。針對UKF在估計電池荷電狀態中存在收斂速度較慢、容易發散等問題，增加了自適應調節因子和衰減因子，該算法估算SOC值誤差精度可小于1%，在估計精度及收斂速度上均優于UKF[51]。

KF克服了安時積分法中SOC估算誤差受SOC初始值影響較大的缺點，且對初始值的精度要求較低，但是其估算值較大程度上依賴建立的電池模型的準確性。

3.2.2 BP神經網絡法

神經網絡法[46]通過調整建立的模型中權重和偏差的方法提高模型的精度。利用BP神經網絡法對電池SOC進行估算，以學習后的網絡作為數學模型，其中輸入層為電池端電壓、充放電電流值、電池溫度和電池內阻；隱含層為系統的激活函數；輸出層為電池的SOC估算值。

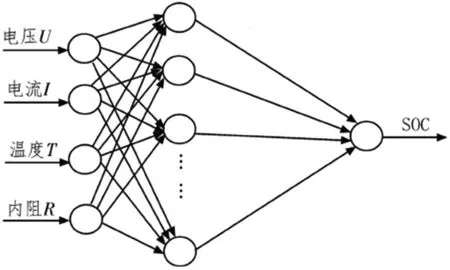
圖5 BP神經網絡結構圖[46]

文獻[52]以動力電池的電壓、電流、溫度和內阻作為輸入，SOC作為輸出，建立4輸入1輸出的神經網絡仿真模型，SOC的預測度為1.6%，比未考慮電池內阻的預測精度提高45%左右。文獻[53]在BP神經網絡法的基礎上采用將混合粒子群（HPSO）結合BP神經網絡的算法，通過優化神經網絡的初始值和閾值克服了種群易陷入局部極小的缺點，加快了收斂速度，減小了SOC預估的誤差。

神經網絡法不需要建立電池的數學模型，適用于所有電池，估算速度快、精度高。但是BP算法需要訓練模型，其訓練數據、訓練方法對SOC估算結果有較大影響。

3.2.3 粒子濾波法

粒子濾波（Particle Filter，PF）通過尋找狀態空間的隨機樣本來近似表示概率密度函數，以樣本均值代替積分運算，PF也是獲得系統狀態的最小方差估計的過程。利用粒子濾波估算鋰電池的SOC的具體計算步驟如下[54]：

狀態空間模型中，鋰電池SOC和鋰電池負載電壓分別為狀態變量和觀測變量。

其中：wk為系統過程噪聲，vk為系統觀測噪聲，Δt為系統采樣周期。

（1）初始化：k=0

p(x0)隨機產生N個粒子

（2）狀態預測

（3）粒子權重計算和歸一化

當系統獲得新的觀測值yk，通過觀測方程獲得新的預測值的誤差計算粒子的權重wi：

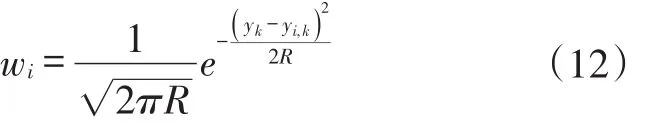
歸一化處理：

（4）重采樣

基于生成的新的隨機樣本分布，通過重采樣復制高概率的粒子，淘汰低概率粒子形成新的樣本分布。重采樣后的粒子權重均為1/N。輸出估計值

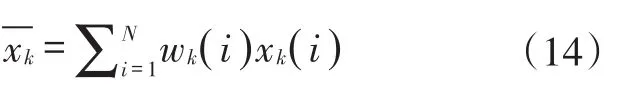
循環迭代重復步驟（2）到（4），實現狀態量xk的遞推估計。

3.3 其他新方法

近年來學者提出了新的估算SOC的方法，比如基于灰色多變量模型[55]、免疫遺傳算法和BP神經網絡相結合[56]、模糊控制法[57]、自適應法和列文伯格-馬奎特算法（Levenberg-Marquardt,LM）結合優化BP神經網絡[58]、遺傳算法（Genetic Algorithm，GA）結合BP神經網絡[59]、隨機森林回歸算法[60]、支持向量機[61]等等。這些算法中大多數都是對上述傳統和新型SOC估算方法中出現的誤差進行修正來提高估算精度。

4 結束語

本文介紹了目前主流的電池等效電路模型和估算SOC的方法。介紹了不同模型和估算SOC方法的原理，比較和分析了不同估算方法間的優缺點。總結出未來SOC估算的發展趨勢如下：

（1）提高硬件的AD采樣精度，以獲得更為接近實際值的電壓、電流、內阻和溫度等參數的樣本數據；

（2）根據現有理論建立更為貼近電池的等效電路模型；

（3）結合SOC估算方法的優缺點和適用范圍，在電池工作的不同階段采用最為合適的SOC估算方法以及采用多種SOC估算方法相結合來提高SOC估算精度。