植被覆蓋條件下的解放閘灌域土壤鹽分衛星遙感估算模型
邱元霖,陳 策,韓 佳,2,王新濤,2,魏世玉,張智韜,2
(1.西北農林科技大學水利與建筑工程學院,陜西 楊凌 712100;2.西北農林科技大學旱區農業水土工程教育部重點實驗室,陜西 楊凌 712100)
0 引 言
河套灌區是我國三大灌區之一,由于干旱半干旱的特殊氣候,加之長期的大水漫灌,造成土壤鹽漬化[1]。解放閘灌域作為河套灌區第二大灌域,土壤鹽漬化一直對農業生產造成負面影響。因此利用準確、有效和快速的技術手段對鹽漬化土壤進行大面積監測具有重要意義,是灌域農業生產健康發展的關鍵[2-4]。
傳統的鹽漬化監測手段雖然精度較高,但難以快速獲取大范圍的土壤鹽漬化信息,且需要耗費大量的人力物力[5]。衛星遙感技術快速、動態、宏觀、綜合的特點,決定了其在土壤鹽漬化監測中的巨大潛力[6]。在利用光譜指數進行土壤鹽漬化監測方面,國內外學者進行了大量的研究[7-10],曹雷等[4]將GF-1號衛星作為數據源,基于表層實測電導率與光譜指數構建了PLSR模型,提高了高分辨率衛星土壤鹽漬化監測的精度。羅沖等[10]利用偏最小二乘法構建了瑪納斯河流域土壤鹽分定量反演模型,對單一時刻的土壤鹽分含量進行了反演,方法經濟、便捷,較好的反映了研究區域的鹽分分布特征。黃權中等[11]基于SI鹽分光譜指數構建了河套灌區鹽分遙感反演模型,在裸土條件下擬合精度較高,驗證精度R2達到0.75。王飛等[9]基于歸一化差值植被指數(NDVI)、鹽分指數(SI)構成了NDVI-SI特征空間,構建了能夠精確反演有植被覆蓋區域土壤鹽分的SDI指數監測模型,研究表明在考慮植被信息后,能夠更好的反應鹽漬化程度。目前土壤鹽分反演的研究多集中于裸土方面,在植被覆蓋條件下的反演研究較少。
因此本文以河套灌區解放閘灌域為研究區域,GF-1號衛星影像為數據源,根據植被受鹽分脅迫時的光譜信息,間接反演土壤鹽分。通過BP神經網絡、分位數回歸、多元線性回歸三種方法建模,確定高分一號衛星數據與不同土壤鹽漬化程度之間的定量關系,并對研究區域土壤鹽漬化分布進行評估,以期提高植被覆蓋條件下的土壤鹽分反演精度,彌補裸土反演連續性上的不足,為土壤鹽漬化監測提供一定的技術支持。
1 材料與方法
1.1 研究區概況
研究區域為內蒙古河套灌區解放閘灌域,灌域位于河套灌區西北部地區,位于北緯40°26′~41°13′、東經106°34′~107°34′,是一個東西長81 km,南北長86 km的斜三角形區域[12],為河套灌區第二大灌域。灌域屬于高原地區,海拔在1 030~1 046 m之間,地形較為平坦。年降雨量66.3~200 mm,年蒸發量1 920~3 450 mm,為干旱半干旱地區[13,14]。灌域南鄰黃河,年引水量約為12 億m3,有夏灌期和秋澆期兩個階段,10月份引水量約占全年的30%,灌域控制面積21.57 萬hm2,灌溉面積12.4 萬hm2[15],農田作物種植結構復雜,主要包括玉米、小麥 、葵花等作物。圖1為研究區地理位置及采樣點分布圖。
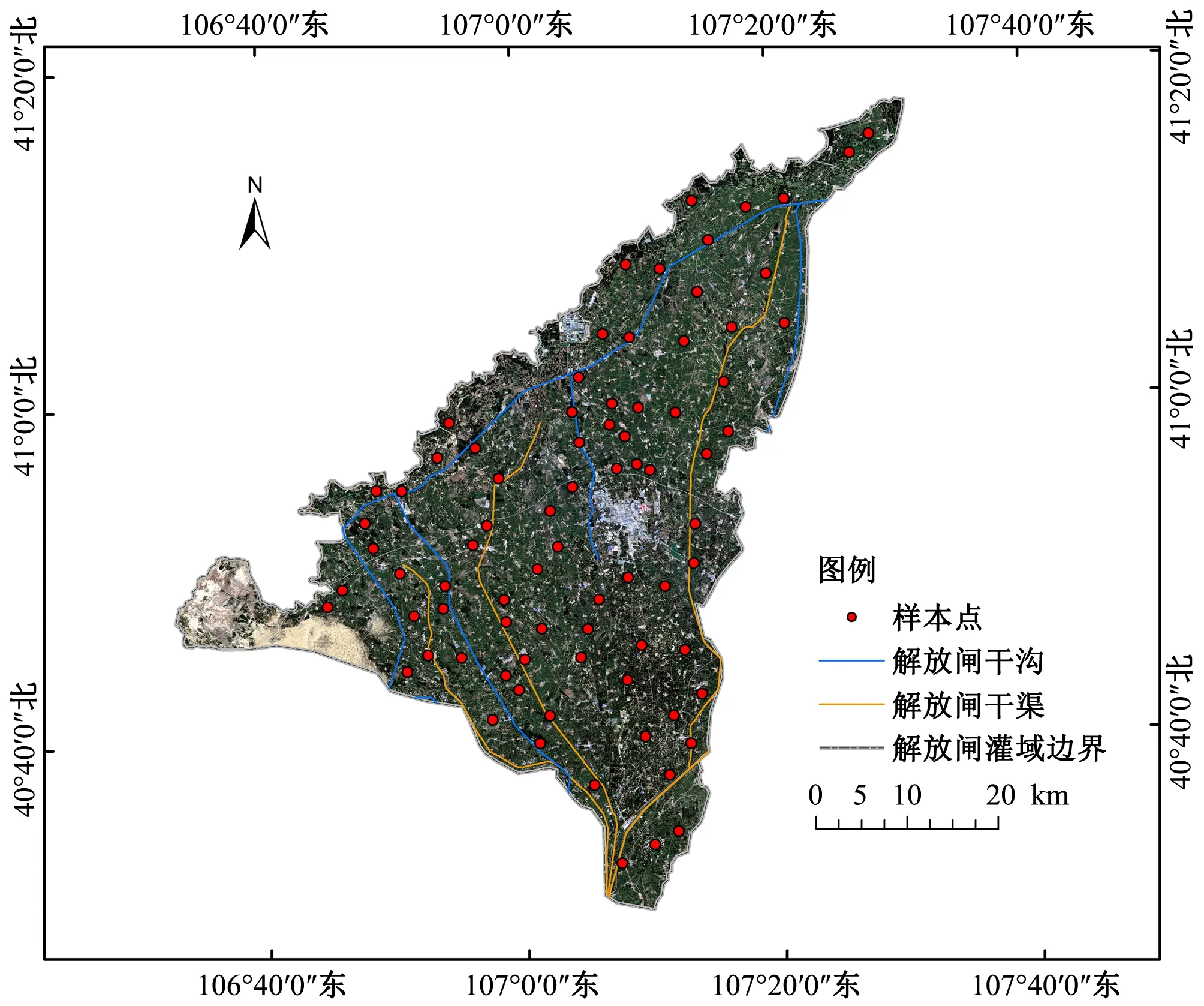
圖1 內蒙古河套灌區解放閘灌域地理位置及采樣點分布圖Fig.1 Geographical location and sampling point distribution map of Jiefangzha irrigation area in Inner Mongolia Hetao Irrigation District
1.2 土壤含鹽量測定
解放閘灌域的主要作物中,葵花、玉米、西葫蘆均于9月20日左右或之后收獲。因此我們選擇作物生長旺盛、植被信息豐富的8月份為研究時段。本文選擇0~60 cm的主根系土壤為研究對象[11,16,17]。研究區域土壤樣本采集時間為2018年8月13-17日,采樣點80個,均為有植被覆蓋的0~60 cm土壤,采樣方法為五點取樣法,即以定位點為中心抽樣點,對角線上與中心樣點等距的4個點為樣點。五點土樣充分混合后,經土水比1∶5配置成水溶鹽溶液。電導率(EC1∶5,μS/m)使用上海佑科儀器公司的DDS-307A電導率儀進行測定,土壤含鹽量(SSC,%)根據經驗公式SSC=(0.288 2EC1∶5+0.018 3)[11]得到。通過隨機選取的方式確定建模集與驗證集,其中2/3的樣本點用于建模(n=53),1/3的樣本點用于驗證(n=27),土壤鹽分統計特征見表1。
表1 土壤鹽分統計特征
Tab.1 Statistical characteristics of soil salinity
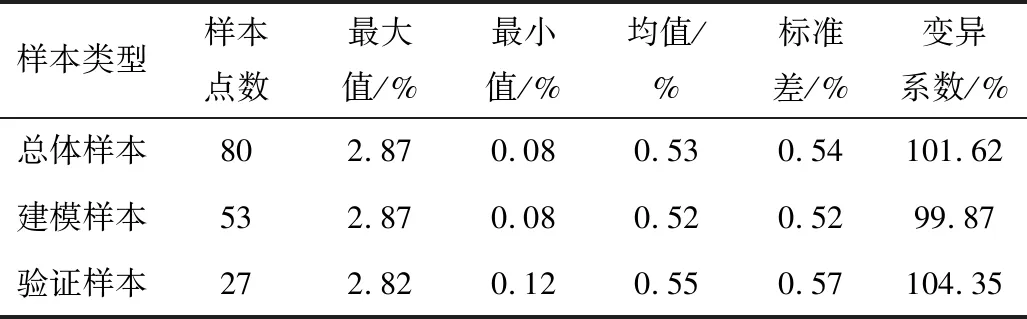
樣本類型樣本點數最大值/%最小值/%均值/%標準差/%變異系數/%總體樣本802.870.080.530.54101.62建模樣本532.870.080.520.5299.87驗證樣本272.820.120.550.57104.35
1.3 影像處理
本文采用GF-1 WFV影像為數據源,衛星空間分辨率16 m,具有藍波段b1(0.45~0.52 μm)、綠波段b2 (0.52~0.59 μm)、紅波段b3(0.63~0.69 μm)、近紅外波段b4(0.77~0.89 μm)4個波段,時間分辨率為4 d。影像獲取時間為2018年8月8日,與采樣時間基本同步,研究區域無云層遮擋。通過ENVI5.3.1軟件進行影像預處理,包括幾何精校正、輻射定標、大氣校正。其中幾何精校正對數據精度影像較大,采用同時期、同區域經過幾何精校正的landsat8影像作為標準,精度為10.59 m,誤差小于1個像元,基本滿足精度要求。
1.4 模型的選擇與構建
本文通過分位數回歸(QR)、多元線性回歸(MLR)、BP神經網絡(BP)3種方法分別建立鹽分反演模型,并進行精度驗證。
1.4.1 多元線性回歸
多元線性回歸(multivariable linear regression)又名多重回歸,是利用兩個及以上自變量(x1,x2,x3,x4,…,xn)對因變量y進行解釋的方法,本文利用SPSS 23軟件進行MLR建模。數學模型如下[18]:
式中:β0為隨機誤差;βi為回歸系數;k為自變量個數。
1.4.2 BP神經網絡
BP神經網絡(back propagation neural network)是由Rumelhart和McClelland為首的科學家在1986年提出的[19],是目前應用領域較廣、較為易懂的神經網絡模型。該模型在非線性映射方面具有很大的優勢,能夠根據輸出結果與期望值之間的誤差調節系統內部的參數值,并依據精度要求反復進行信號向前傳播誤差反向傳播的操作,最終得到輸出結果。BP神經網絡模型拓撲結構由輸入層、隱含層、輸出層3部分組成[18,20,21]。本文BP神經網絡模型以NIR、SI2、S2、S3、EVI為輸入層,土壤鹽分為輸出層。利用SPSS23軟件進行BP神經網絡建模。
1.4.3 分位數回歸
分位數回歸(Quantile regression)是在自變量與因變量的條件分位數之間建立關系的回歸方法,最早由Roger Koenker和Gilbert Bassett提出,此方法對異常點具有較高的耐抗性,且模型不需要對分布進行假設,使其較為穩健[22,23]。本文利用SPSS 23軟件進行QR建模。
1.5 精度驗證
對于模型的評價主要采用R2、RMSE、MAE三個指標。其中R2為決定系數(coefficient of determination),用于衡量模型的擬合精度。RMSE為均方根誤差(root mean square error)、MAE為平均絕對誤差(mean absolute error),二者通過檢驗模型預測值與實測值之間的誤差來衡量模型的準確性。R2越大、RMSE與MAE越小,模型的精度越高。相關公式如下:
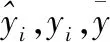
1.6 數據處理
本文數據提取采用ENVI5.3.1軟件完成,數據處理及分析采用Microsoft Office 2016軟件完成,模型擬合采用SPSS 23軟件完成,繪圖采用Origin 2017軟件完成。
2 結果與分析
2.1 光譜指數敏感性分析
為能更全面的反應植被覆蓋時的土壤鹽分信息,考慮到不同光譜指數反饋信息不同的特點,本文依據前人經驗[4,24,25]選取鹽分指數(SI2、S2、S3)、增強植被指數(EVI)、近紅外NIR波段作為輸入因子,并進行敏感性分析(圖2)。模型輸出因子為采樣點0~60 cm處的土壤含鹽量(SSC,%)。指數均由ENVI5.3.1平臺提取80個采樣點的各波段反射率計算得到,計算公式如表2所示。
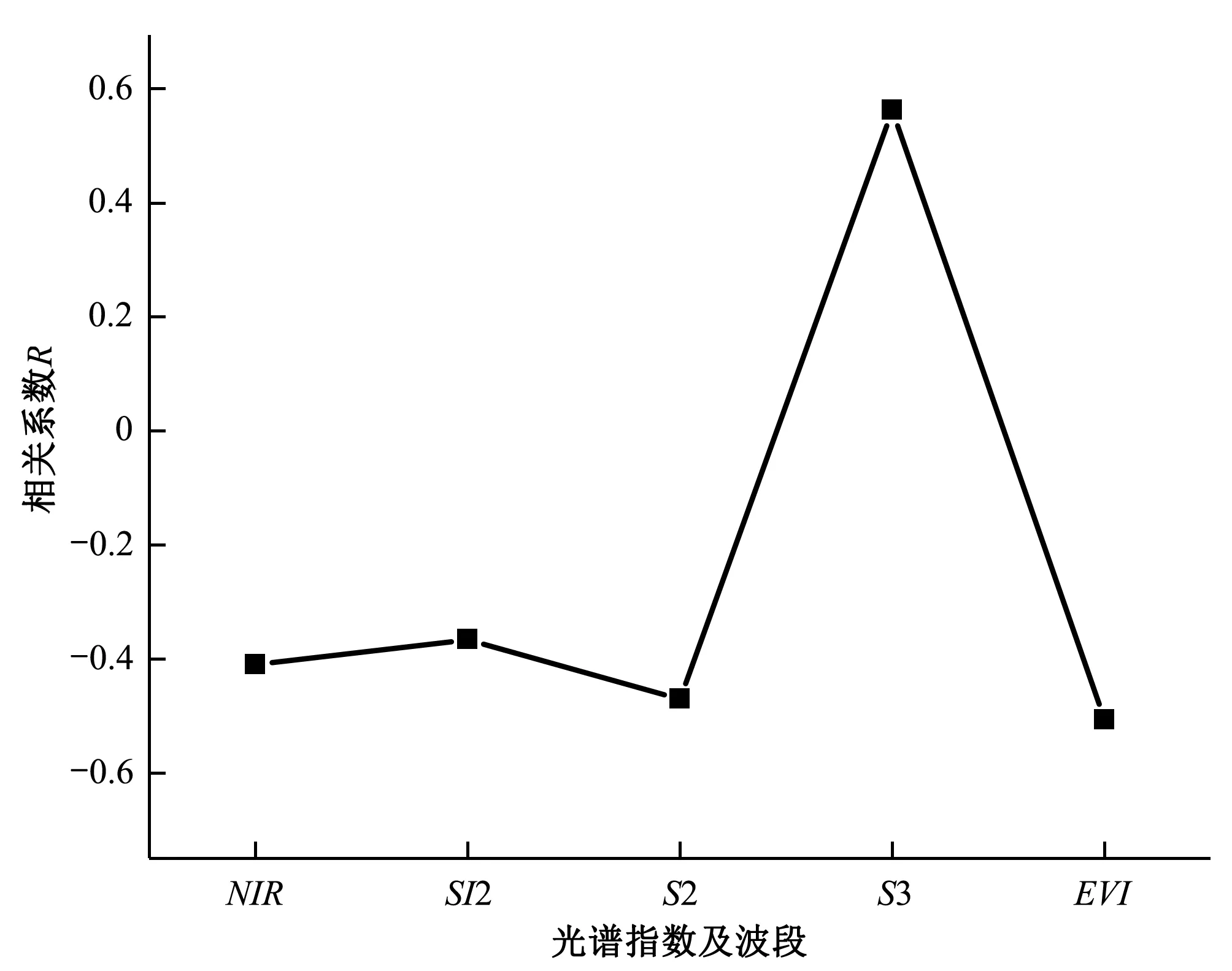
圖2 光譜指數及波段相關系數折線圖Fig.2 Spectral index and band correlation coefficient line chart
表2 光譜指數
Tab.2 Spectral Index

光譜指數計算公式參考文獻SI2G2+R2+NIR2[24]S2(B-R)/(B+R)[4]S3(G×R)/B[4]EVI2.5×NIR-RNIR+6R-7.5B+1()[25]
注:B為藍波段b1;G為綠波段b2;R為紅波段b3;NIR為近紅外波段b4。
五個指數均通過了P=0.01的顯著性檢驗。其中只有S3與土壤鹽分成正相關,且相關系數達到0.555,對土壤鹽分的敏感性最好。EVI作為唯一的植被指數對土壤的敏感性僅次于S3,相關系數為-0.506。鹽分指數S2與SI2相關系數分別為-0.470、-0.366,對土壤鹽分較為敏感。近紅外NIR波段相關系數為-0.409。選取以上五個指數作為因變量建立土壤鹽分反演模型。
2.2 建模集精度分析
基于SPSS 23軟件分別利用多元線性回歸(MLR)、分位數回歸(QR)、BP神經網絡(BP)建立土壤鹽分反演模型,模型擬合精度數據如表3所示。
表3 基于光譜指數的多元線性回歸、神經網絡、分位數回歸模型擬合精度對比
Tab.3 Comparison of fitting precision of MLR, BP and QRmodels based on spectral index
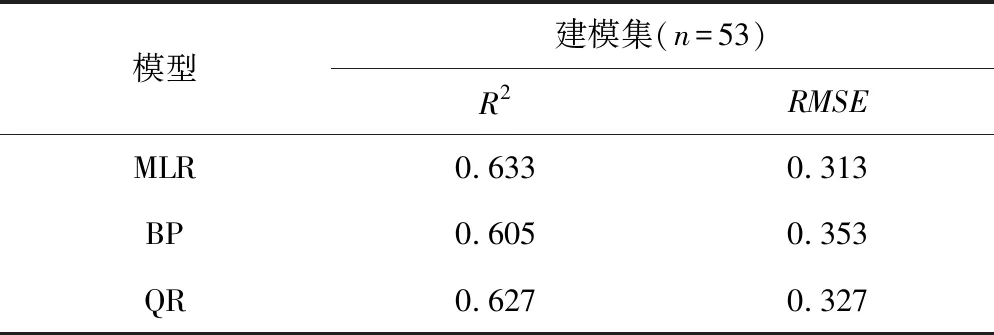
模型建模集(n=53)R2RMSEMLR0.6330.313BP0.6050.353QR0.6270.327
由表3得3個模型擬合精度都較好,決定系數均在0.6以上;BP神經網絡模型擬合精度相對其他兩個模型較差,決定系數最低為0.605,RMSE也高于其他兩個模型,為0.353,預測值的偏差相對較大;多元線性回歸模型與分位數回歸模型的擬合精度較高,二者決定系數均優于0.62,其中多元線性回歸模型決定系數相對較高,為0.633,分位數回歸模型決定系數略低,為0.627,且多元線性回歸模型與分位數回歸模型的RMSE效果也相對較好,多元線性回歸模型的RMSE為0.313,相對于實測值誤差較小,優于分位數回歸模型的RMSE=0.327。綜合比較上述模型,多元線性回歸模型的擬合精度最好,決定系數和RMSE均為最優,但分位數回歸模型與之相差不大,決定系數近似相等,RMSE僅比多元線性回歸模型高4.47%,因此兩個模型在擬合精度上無明顯的優劣之分,均能較好的在植被覆蓋條件下反演土壤鹽分。
2.3 模型預測精度分析
將驗證集的樣本點代入到已經建立的3個土壤鹽分反演模型當中,通過計算決定系數R2、均方根誤差RMSE和平均絕對誤差MAE,檢驗3個模型的預測效果并進行精度分析。相關計算結果如表4所示。
表4 基于光譜指數的多元線性回歸、神經網絡、分位數回歸模型預測精度對比
Tab.4 Comparison of prediction accuracy of MLR, BP and QRmodels based on spectral index
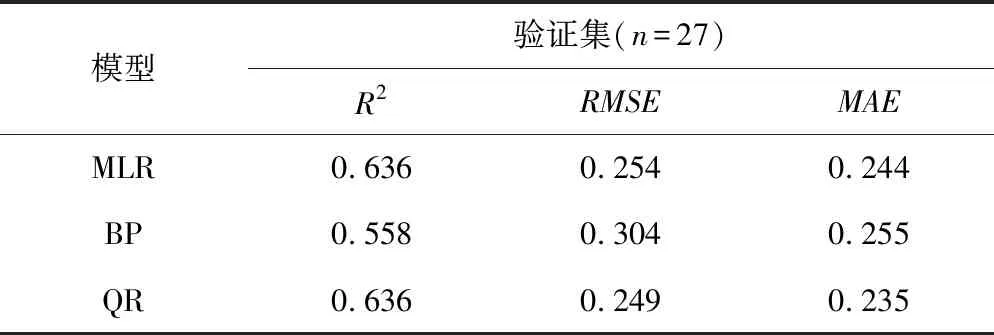
模型驗證集(n=27)R2RMSEMAEMLR0.6360.2540.244BP0.5580.3040.255QR0.6360.2490.235
多元線性回歸模型與分位數回歸模型的預測精度依然相對較好,與建模集情況相同,決定系數均達到0.636。其中分位數回歸模型RMSE相對較低,為0.249,略小于多元線性回歸模型,就MAE而言分位數回歸模型比多元線性回歸模型低3.68%,效果相對較好,這說明分位數回歸模型預測值與實測值誤差整體較小。BP神經網絡模型決定系數明顯低于其他兩個模型,僅為0.558,同時RMSE與MAE數值相較其他兩個模型偏大,整體預測精度偏低。因此分位數回歸模型在滿足擬合優度的基礎上,對土壤鹽分的預測相對誤差較低,反演精度更高。
如圖3所示,當SSC<0.5時,BP模型的整體預測精度最低,MLR模型次之,QR模型預測值更接近實測值;0.5
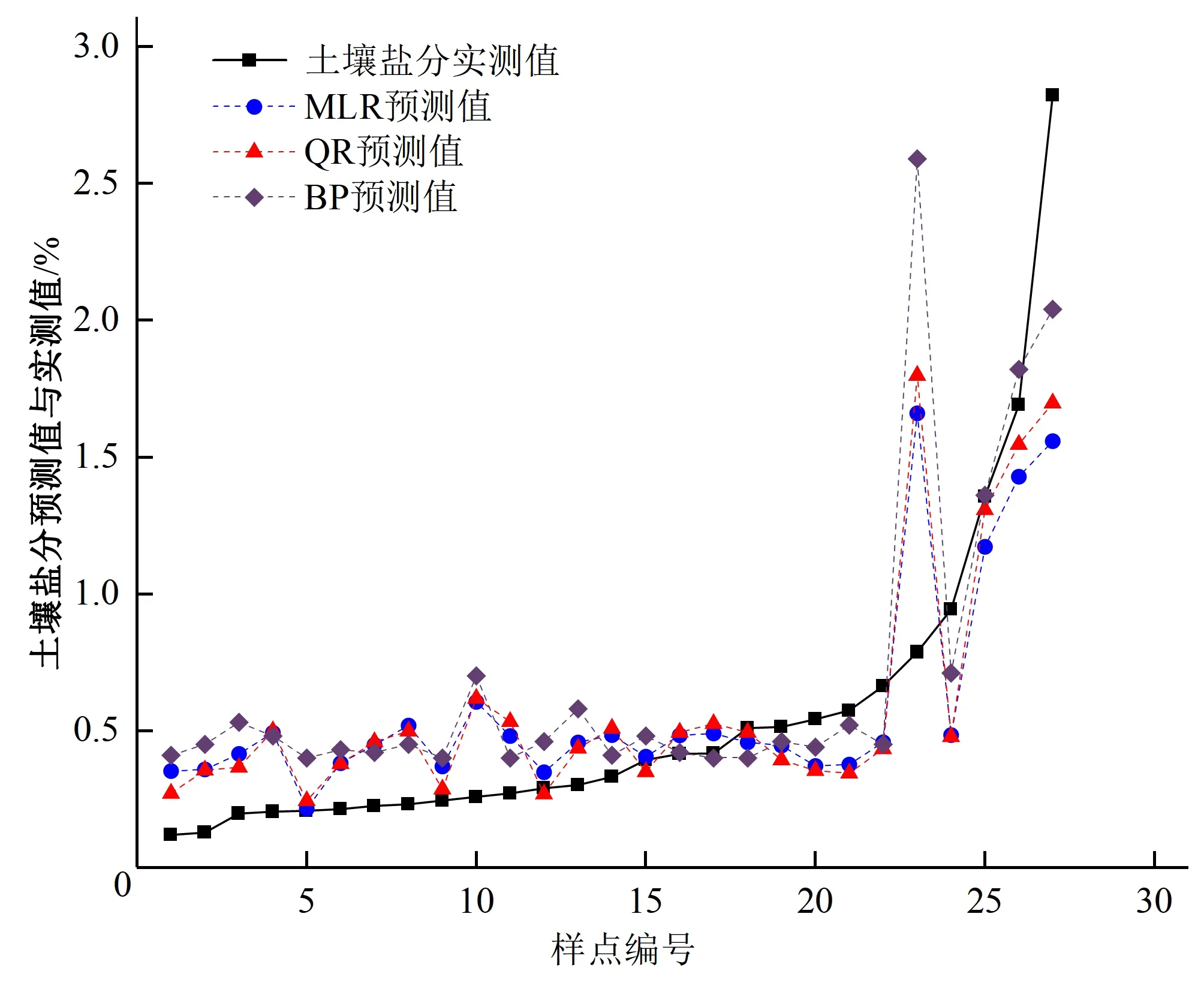
圖3 多元線性回歸、BP神經網絡、分位數回歸模型土壤鹽分預測值與實測值折線圖Fig.3 Line diagram of predicted and measured values of soil salinity in MLR, BP and QR models
2.4 土壤鹽度空間分布
選取預測精度最高的QR模型對土壤鹽分進行反演,得到內蒙古河套灌區解放閘灌域的0~60 cm土壤鹽分分布圖(圖4)。根據QR模型反演結果,解放閘灌域非鹽土(<0.2%)、輕度鹽漬化(0.2%~0.5%)、重度鹽漬化(0.5%~1.0%)與鹽土(>1.0%)面積分別占灌域總面積的27%、38%、12%、7%,城市用地約占16%。灌域南部地區的土壤含鹽量普遍較低,多數為非鹽土(<0.2%),輕度鹽漬化區域穿插分布其間。從灌域中部地區開始到灌域北部地區結束,非鹽土較少,多為輕度鹽漬化。灌域西側集中分布有大面積的鹽土,且多為裸土區域,其他重度鹽漬化區域及鹽土則零散的分布在整個灌域,其中杭錦后旗西北與東南兩側和灌域北部區域分布相對較多;這與灌域南部地區地下水位較深,中部地區水位較淺有一定關系。
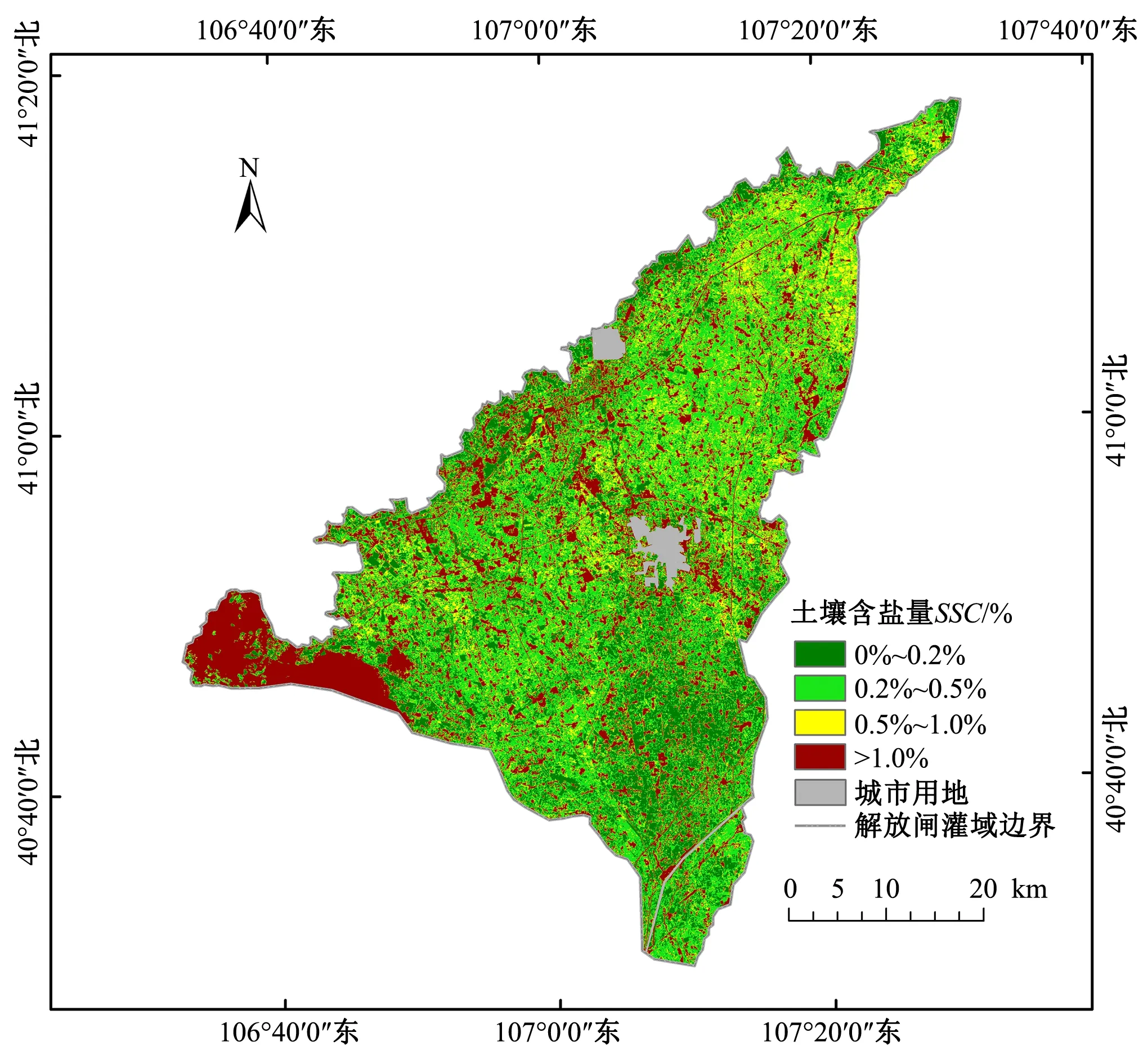
圖4 解放閘灌域0~60 cm土壤鹽分空間分布圖Fig.4 Spatial distribution of soil salinity in 0~60 cm of Jiefang irrigation area
3 結 語
(1)經過對比3個不同的鹽分反演模型,發現多元線性回歸模型與分位數回歸模型均能較好的反演植被覆蓋條件下0~60 cm層土壤鹽分,二者建模與驗證決定系數均在0.6以上,其中分位數回歸預測精度最高,是本次土壤鹽分估算的最優模型。
(2)通過分析河套灌區解放閘灌域鹽分反演圖,就0~60 cm土壤而言,研究區整體鹽分分布情況為灌域南部地區土壤鹽漬化程度較輕。重度鹽漬化及鹽土區域呈零散狀分布在整個灌域,占灌域總面積的19%左右。
(3)通過衛星遙感手段提取作物光譜信息進而間接反演土壤鹽分受到天氣諸多因素的影響,本文的研究方法僅適用于作物生長茂盛的時期,其他生育期的鹽分反演還需進一步探究。

