無窮方差序列均值變點的Ratio檢驗

皮林,王丹

(西北大學數學學院,陜西 西安 710127)

1 引言

統計學中,變點問題一直是一個熱點課題,一般認為變點問題的研究始于Page[1]在 Biometrika上發表的一篇關于連續抽樣檢驗的文章.文獻[2]指出 “變點τ0是指在一個序列或過程中,在某個未知時刻τ0,序列或過程的某個統計特性發生了變化”.變點問題的統計推斷就是依據具體的背景,對這個未知的時刻τ0做出估計,并對估計量的性質進行統計分析.

在現實中,變點問題不但在早期的工業自動控制上有大量應用,而且,隨著近年來對變點問題的不斷深入研究,變點問題的實際應用現在已經拓展到了許多其他領域.如在經濟學上,文獻[3]基于Schwarz信息準則的統計變點檢測,對影響國際天然鈾價格的因素進行了分析;文獻[4]基于Copula模型進行變點檢測,分析了投資者的情緒傳染;在網絡安全上,基于變點檢測,文獻[5]實現了對網絡移動目標防御的安全成本和安全收益的實時檢測和動態度量;在航空技術上,文獻[6]通過順序雙滑窗的航空器軌跡變點檢測,實現了對航空器飛行階段的有效劃分;在金融上,文獻[7]通過對c-D-Copula模型進行變點檢測,對美國次貸危機金融傳染的存在性和變化過程進行了研究;文獻[8]通過對R藤copula進行變點檢驗,分析了系統性風險對金磚四國影響的結構性變化;在氣候監測上,文獻[9]通過建立似然比變點模型和回歸變點模型,對當年最大風速序列的變點進行檢驗和估計.

變點不僅具有廣泛的實際應用,而且在理論上也有較大的研究價值,針對變點問題,在理論研究方面涉及了統計學的眾多方向,比如結合了質量控制理論,估計理論,假設檢驗理論,Bayes理論等,所以一直是統計學中的一個熱門課題,取得了豐碩的研究成果,如文獻[10]研究了正態線性回歸模型和獨立的Student-t線形回歸模型,采用SIC準則定位模型的變點位置;文獻[11]利用AIC(Akaike information criterion)信息準則討論了Gauss分布變點的檢測;文獻[12]研究了隨機誤差項為獨立同分布序列的變點問題;文獻[13]采用CUSUM方法研究獨立時間序列的變點估計問題；文獻[14]對獨立隨機序列的變點問題進行了研究.

然而,現有文獻對變點的研究主要集中于方差有限及隨機誤差項為獨立同分布序列的統計模型,對無窮方差重尾序列均值變點的研究較少.本文研究的重尾序列{Yt},其特征指數κ滿足κ∈(1,2),此時{Yt}序列均值存在,方差不存在,事實上,許多金融資產收益率的分布都具有重尾特性,由于受突發事件的影響,而在某個未知的時刻序列發生突變,從而造成金融資產可能的損失,所以,針對重尾序列變點的檢驗就顯得尤為重要.基于此,本文提出無窮方差序列均值變點的Ratio檢驗,通過殘量累積平方和的比率構造檢驗統計量,并在原假設下得到了檢驗統計量的極限分布,在備擇假設下證明了檢驗的相合性,然后通過Monte Carlo模擬說明檢驗方法的有效性.

2 模型與假設

考慮如下模型:

其中u(t)是非隨機函數,{Yt}是滿足如下假設的重尾序列.

假設 2.1隨機變量序列{Yt}是嚴平穩序列,尾指數κ∈(1,2)且EYt=0.

引理 2.1若假設2.1成立,則

其中an=inf{x:p(|Yt|>x)6n?1},{U(τ)}是 [0,1]上的κ-穩定 Lévy 過程,符號表示依分布收斂.

注 2.1該結果是文獻[15-16]得到的,Lévy過程U(τ)的具體定義在下文中并不需要,但an可表示為

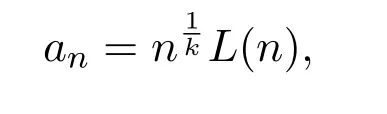
其中L是一個緩慢變化函數.

考慮如下假設檢驗問題:

其中u1,u2是未知常數且u12,τ0∈(0,1),n是樣本容量,[·]表示取整函數.在原假設下,重尾序列{Xt}沒有均值變點,在備擇假設下,重尾序列{Xt}在[nτ0]處有一個均值變點.

這里，我們為大家介紹四種適合用來處理人像照片的色彩效果——當然了，用來處理任意一種類型的照片也沒有問題。這些色彩風格最棒的一點就是它們雖然最適合于人像，但并不局限于此。

3 主要結果

令{U(t)}是 [0,1]上的k-穩定 Lévy過程,并定義如下兩個過程

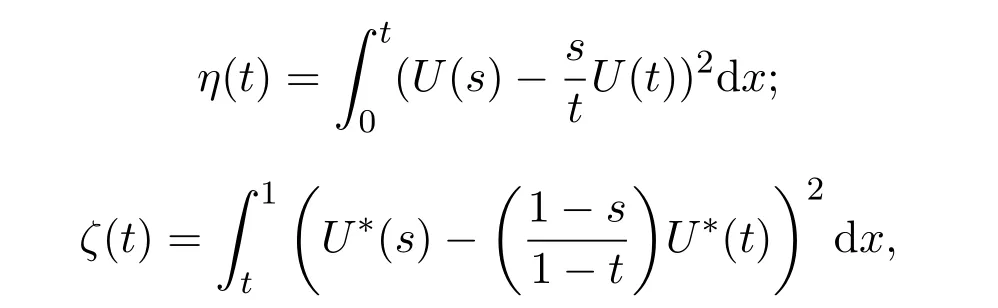
其中U?(t)=U(1)?U(t).

基于CUSUM函數,構造如下檢驗統計量:

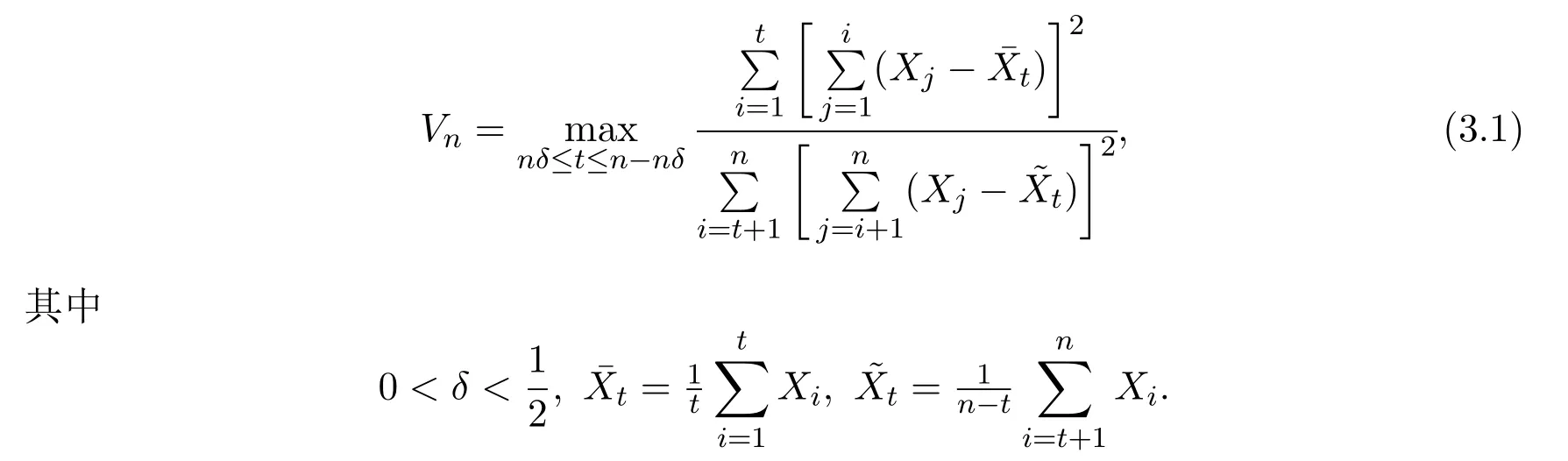
提出如下定理:

定理 3.1若假設2.1成立,則在原假設H0下有

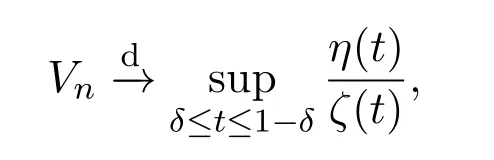
證明不失一般性,假設u1=0,則在原假設H0下,Xt=Yt,其中定義同前文一致,首先考慮檢驗統計量Vn的分子,有

4 數值模擬

4.1 檢驗的臨界值

用數值模擬研究重尾序列均值變點Ratio檢驗,其中顯著性水平α=0.05,0.10,樣本容量n=200,500,1000.重尾序列由Nolan教授程序生成,具體可見Nolan教授個人主頁.針對不同的樣本容量n,通過把重尾數據帶入統計量Vn,分別重復進行2000次得到2000個樣本,這些2000個樣本的經驗分位數可以近似為統計量Vn在原假設下的臨界值V,若Vn>V,則拒絕原假設.

4.2 檢驗的經驗水平和經驗勢函數

假設檢驗問題:

其中u1=0,u2=0,1,1.5,2,若u2=0,則序列不存在變點,若u2=1,1.5,2,則序列存在結構變點.令τ0=0.48,誤差序列{Yt}為

獨立同分布序列{Zt}是重尾數據,κ=1.16,1.97,序列{Zt}滿足假設 2.1,其中取?1=1,?2=?0.5,在隨機變量序列{Yt}為二階自回歸序列AR(2)和獨立同分布過程下分別進行模擬.

對樣本容量為n=200,500,1000的數據分別重復實驗5000次,檢驗的經驗水平和經驗勢函數值用實驗5000次中拒絕原假設的頻率來近似.模擬的經驗水平和經驗勢函數值分別見表1、表2、表3和表4.經驗水平值是在原假設成立下,拒絕原假設的概率,經驗勢函數值是在備擇假設成立下,拒絕原假設的概率.

表1 H0下的經驗水平值,{Yt}=AR(2)

表2 H0下的經驗水平值,{Yt}=i.i.d

表3 H1下的勢函數值,{Yt}=AR(2)

表4 H1下的勢函數值,{Yt}=i.i.d

通過模擬可知的主要結論:

(1)從表1-表 2可以看出,在沒有變點的情況下,經驗水平值是接近于顯著性水平α的.且樣本容量n越大,檢驗水平值越接近于顯著性水平α,說明水平失真越小,檢驗有效.而且,獨立同分布序列的經驗水平值大于AR(2)序列.

(2)從表3-表4了解到,對于一個固定的數n,隨著u2的不斷增大,勢函數值也相應地不斷增大,對于一個固定的u2,勢函數值隨著樣本容量n的增大而增大,隨著樣本容量n和u2的增加,勢函數值逼近1.

(3)結合表1-表4,κ=1.97的結果優于κ=1.16,這是因為特征指數k刻畫的是重尾序列的特性:指數k越小,取到“奇異點”的概率越大.

5 結論

本文通過殘量累計平方和的比率構造統計量檢驗無窮方差序列的均值變點.基于CUSUM函數,通過Ratio檢驗方法,利用殘量累計平方和的比率構造出檢驗統計量,在原假設條件成立時,殘量累計平方和比率檢驗統計量的極限分布是一個Lévy過程函數.均值變點檢驗方法中的統計量大多為差值形式,數值模擬的結果表明,對于無窮方差序列的均值變點檢驗問題,基于CUSUM函數,通過殘量累計平方和的比率構造出統計量的檢驗方法勢函數表現優良,說明該方法有效.