強(qiáng)乘積圖的Euler性

陰浩然李峰

(1.青海師范大學(xué)計(jì)算機(jī)學(xué)院,青海 西寧 810008;2.青海省藏文信息處理與機(jī)器翻譯重點(diǎn)實(shí)驗(yàn)室,青海 西寧 810008;3.藏文信息處理教育部重點(diǎn)實(shí)驗(yàn)室,青海 西寧 810008)

1 引言

圖G=(V(G),E(G)),其中V(G)是G的非空頂點(diǎn)集,E(G)?V(G)×V(G)是G的邊集.|V(G)|是圖G中的頂點(diǎn)數(shù)目,稱為圖G的階.對(duì)于任意頂點(diǎn)x∈V(G),記圖G中所有與x相鄰的頂點(diǎn)的集合為NG(x),dG(x)=|NG(x)|表示x在G中的度數(shù).本文所考慮的圖都是簡(jiǎn)單連通無向圖,未說明的記號(hào)和術(shù)語可參見文獻(xiàn)[1].

圖G的一條途徑是指一個(gè)頂點(diǎn)和邊交替組成的有限非空序列

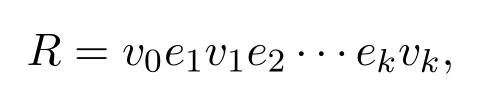
使得邊ei的端點(diǎn)為vi?1和vi,i=1,2,···,k.其中頂點(diǎn)v0和vk分別稱為途徑R的起點(diǎn)和終點(diǎn),而v1,v2,···,vk?1稱為R的內(nèi)部頂點(diǎn).如果途徑R中的邊e1,e2,···,ek互不相同,那么R稱為跡.經(jīng)過圖G中每條邊的跡稱為G的Euler跡.起點(diǎn)和終點(diǎn)不同的Euler跡稱為Euler通路.起點(diǎn)和終點(diǎn)相同的Euler跡稱為Euler環(huán)游,即Euler環(huán)游是閉的 Euler跡.如果一個(gè)圖包含 Euler環(huán)游,那么這個(gè)圖稱為 Euler圖.因?yàn)楹?jiǎn)單圖中的任意兩頂點(diǎn)之間至多有一條邊,所以途徑v0e1v1e2···vkek由它的頂點(diǎn)序列v0v1···vk所確定,因此簡(jiǎn)單圖的途徑可用其頂點(diǎn)序列來表示.

強(qiáng)乘積圖的概念是文獻(xiàn)[2]首先提出的.兩個(gè)無向圖

的強(qiáng)乘積是一個(gè)無向圖,記為G1?G2.它的頂點(diǎn)集為

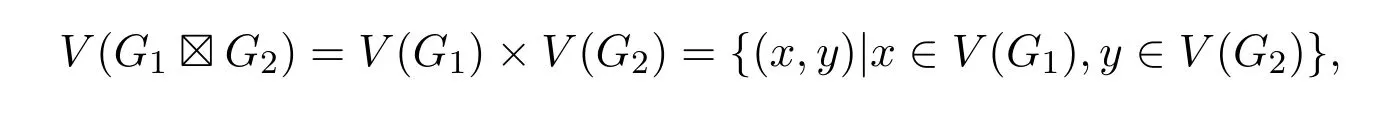
任意兩個(gè)不同的頂點(diǎn) (x1,y1)和 (x2,y2)(其中x1,x2∈V(G1),y1,y2∈V(G2))相鄰當(dāng)且僅當(dāng)x1=x2且 (y1,y2)∈E(G2),或者y1=y2且 (x1,x2)∈E(G1),或者(x1,x2)∈E(G1)且(y1,y2)∈E(G2).圖G1和G2稱為強(qiáng)乘積圖G1G2的因子.由強(qiáng)乘積構(gòu)造出來的大圖包含乘積因子圖作為它的子圖,并且保留了因子圖的許多好性質(zhì),比如,連通性、點(diǎn)可遷性、可嵌入性等(見文獻(xiàn)[3-5]).更多關(guān)于強(qiáng)乘積的知識(shí)可見文獻(xiàn)[2-7].

瑞士數(shù)學(xué)家Euler于1736年發(fā)表了一篇論文“哥尼斯堡的七座橋”,不僅解決了著名的“七橋問題”,更開創(chuàng)了數(shù)學(xué)的一個(gè)新分支—圖論.關(guān)于一個(gè)圖的Euler環(huán)游存在性、求解和計(jì)數(shù)問題引起了許多作者的興趣.1999年,文獻(xiàn)[8]研究了完全圖K2m的 Euler環(huán)游構(gòu)造問題,并且給出了一個(gè)求解該類圖Euler環(huán)游的算法.2010年,文獻(xiàn)[9]研究了二部圖的Euler環(huán)游問題,并對(duì)該類圖的Euler環(huán)游數(shù)目和性質(zhì)進(jìn)行了刻畫.更多關(guān)于Euler圖的知識(shí)可見文獻(xiàn)[10-11].

本文主要是研究強(qiáng)乘積圖中Euler環(huán)游和Euler通路的存在性問題.因?yàn)閺?qiáng)乘積圖G1G2是由乘積因子圖G1和G2構(gòu)造出來的,所以因子圖G1和G2的拓?fù)浣Y(jié)構(gòu)必然會(huì)影響著強(qiáng)乘積圖G1G2的拓?fù)浣Y(jié)構(gòu).研究強(qiáng)乘積圖的Euler跡問題時(shí),也就是研究乘積因子圖的拓?fù)浣Y(jié)構(gòu)對(duì)強(qiáng)乘積圖Euler跡存在性的影響.據(jù)此,本文給出了強(qiáng)乘積圖含有Euler環(huán)游和Euler通路的一個(gè)充分必要條件。

2 主要定理及證明

定理 2.1設(shè)G1和G2是兩個(gè)非平凡的連通圖.強(qiáng)乘積圖G1G2是Euler圖當(dāng)且僅當(dāng)G1和G2中的每個(gè)頂點(diǎn)的度數(shù)是偶數(shù).

證明設(shè)G1和G2中的每個(gè)頂點(diǎn)的度數(shù)是偶數(shù).由于G1和G2都是非平凡的連通圖,根據(jù)強(qiáng)乘積的定義,易知強(qiáng)乘積圖G1G2也是非平凡的連通圖.設(shè)T是G1G2的所有跡中最長(zhǎng)的一條,并且記為以下形式

可以斷言

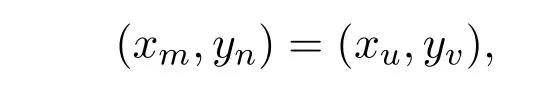
如若不然,跡T終止于(xm,yn)(xu,yv).根據(jù)跡的定義,跡T的終點(diǎn)(xm,yn)可能作為T的內(nèi)部頂點(diǎn)出現(xiàn)過多次,并且每出現(xiàn)一次都會(huì)關(guān)聯(lián)強(qiáng)乘積圖G1G2的兩條邊.又因?yàn)檑ET終止于頂點(diǎn)(xm,yn),所以可以得到頂點(diǎn)(xm,yn)與奇數(shù)條邊相關(guān)聯(lián).由于頂點(diǎn)xm∈V(G1)和yn∈V(G2)的度數(shù)為偶數(shù),根據(jù)強(qiáng)乘積圖的定義有

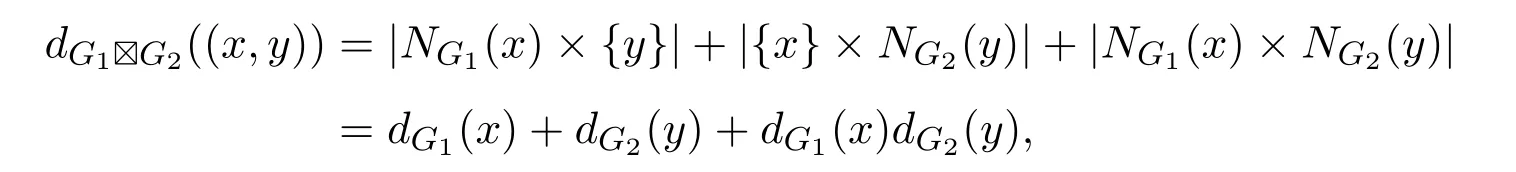
因此頂點(diǎn)(xm,yn)的度數(shù)為偶數(shù).更一般地,可以得到強(qiáng)乘積圖G1G2中任意頂點(diǎn)的度數(shù)是偶數(shù).由此可知頂點(diǎn)(xm,yn)至少還關(guān)聯(lián)一條不在跡T中的邊,假設(shè)這條邊為((xm,yn),(xm+1,yn+1)).此時(shí),可以得到一條比T更長(zhǎng)的跡T+(xm+1,yn+1),這矛盾于T是最長(zhǎng)跡.因此強(qiáng)乘積圖G1G2的最長(zhǎng)跡T是一條起點(diǎn)和終點(diǎn)相同的跡,即閉跡.設(shè)C=T并且記為

C是G1G2的最長(zhǎng)跡且是閉跡.如果C包含強(qiáng)乘積圖G1G2的所有邊,那么C是G1G2的一個(gè) Euler環(huán)游,即強(qiáng)乘積圖G1G2是 Euler圖.否則,假設(shè)C未包含G1G2所有的邊.因?yàn)镚1G2是連通的,所以一定存在著某條不在C中的邊e=((xb,yd),(xi,yj))與C上的頂點(diǎn)(xb,yd)相關(guān)聯(lián).設(shè)H=G1G2?E(C),即圖H是由強(qiáng)乘積圖G1G2刪去C中的邊而得到的.取H中包含邊e的連通分支H1,H1是非平凡且連通的.因?yàn)殚]跡C中的每個(gè)頂點(diǎn)關(guān)聯(lián)G1G2的偶數(shù)條邊,所以圖H中的每個(gè)頂點(diǎn)度也關(guān)聯(lián)著偶數(shù)條邊,對(duì)于連通分支H1亦是如此.現(xiàn)考慮H1中起始于頂點(diǎn)(xb,yd)的一條最長(zhǎng)跡.利用上述相似方法,可知這條最長(zhǎng)跡必須終止于起點(diǎn) (xb,yd),記這條閉跡為C′.據(jù)此,在閉跡C到達(dá)頂點(diǎn)(xb,yd)時(shí),把C′粘到C上,可以得到一個(gè)比C更長(zhǎng)的閉跡,這導(dǎo)致矛盾.因此,C包含了強(qiáng)乘積圖G1G2所有的邊,從而C是G1G2的一個(gè)Euler環(huán)游,即強(qiáng)乘積圖G1G2是Euler圖.

反之,設(shè)強(qiáng)乘積圖G1G2是Euler圖,C′是G1G2的一個(gè)Euler環(huán)游,記為

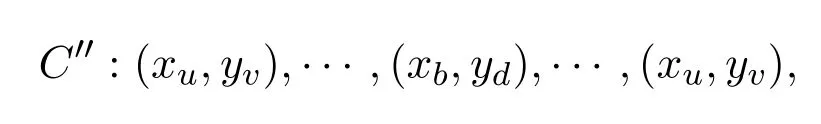
頂點(diǎn) (xb,yd)是 Euler環(huán)游C′的內(nèi)部頂點(diǎn) (可能存在 (xb,yd)=(xu,yv)).根據(jù) Euler環(huán)游的定義,易知(xb,yd)作為C′的內(nèi)部頂點(diǎn)每出現(xiàn)一次,就會(huì)有強(qiáng)乘積圖G1G2中兩條邊與之關(guān)聯(lián).因?yàn)镋uler環(huán)游C′包含了G1G2中所有的邊,所以對(duì)于強(qiáng)乘積圖中的頂點(diǎn) (xb,yd)(xu,yv),有偶數(shù)條邊與之相關(guān)聯(lián).又因?yàn)镋uler環(huán)游C′是起始并且終止于頂點(diǎn)(xu,yv)的,所以與頂點(diǎn)(xu,yv)相關(guān)聯(lián)的邊的條數(shù)也為偶數(shù).綜合上面的討論,對(duì)于強(qiáng)乘積圖G1G2中的任意頂點(diǎn)(xi,yj),與它相關(guān)聯(lián)的邊的條數(shù)為偶數(shù),即G1G2中的任意頂點(diǎn)(xi,yj)的度數(shù)是偶數(shù).又因?yàn)?/p>

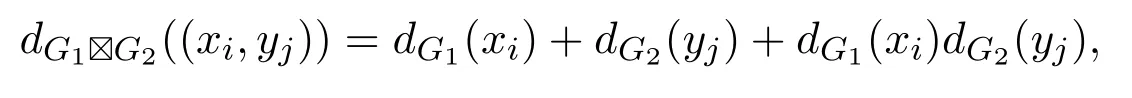
因而可以得到G1的任意頂點(diǎn)xi的度數(shù)為偶數(shù)且G2的任意頂點(diǎn)yj的度數(shù)也為偶數(shù),即G1和G2中的每個(gè)頂點(diǎn)的度數(shù)是偶數(shù).

定理 2.2設(shè)G1和G2是兩個(gè)連通圖.

(1)如果G1中每個(gè)頂點(diǎn)的度數(shù)都是偶數(shù)且G2恰有兩個(gè)度數(shù)為奇數(shù)的頂點(diǎn),那么在強(qiáng)乘積圖G1G2中存在k=|V(G1)|條邊不交的跡T1,T2,···,Tk,使得

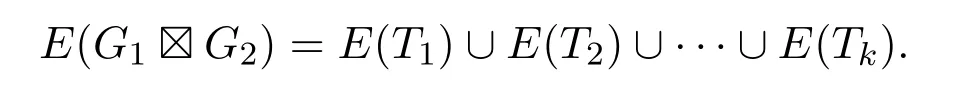
(2)如果G2中每個(gè)頂點(diǎn)的度數(shù)都是偶數(shù)且G1恰有兩個(gè)度數(shù)為奇數(shù)的頂點(diǎn),那么在強(qiáng)乘積圖G1G2中存在k=|V(G2)|條邊不交的跡T1,T2,···,Tk,使得

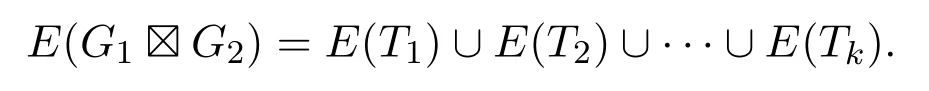
證明僅證明(1),(2)可類似證明.設(shè)圖G1的每個(gè)頂點(diǎn)的度數(shù)都是偶數(shù)且G2恰有兩個(gè)度數(shù)為奇數(shù)的頂點(diǎn).由于圖G1和G2都是連通圖,根據(jù)強(qiáng)乘積定義,易知強(qiáng)乘積圖G1G2是連通且非平凡的.令k=|V(G1)|,設(shè)G1的頂點(diǎn)為x1,x2,···,xk,G2的兩個(gè)度數(shù)為奇數(shù)的頂點(diǎn)為y1和y2.對(duì)于強(qiáng)乘積圖G1G2的任意頂點(diǎn)(x,y),其中x∈V(G1),y∈V(G2),根據(jù)強(qiáng)乘積的定義可知

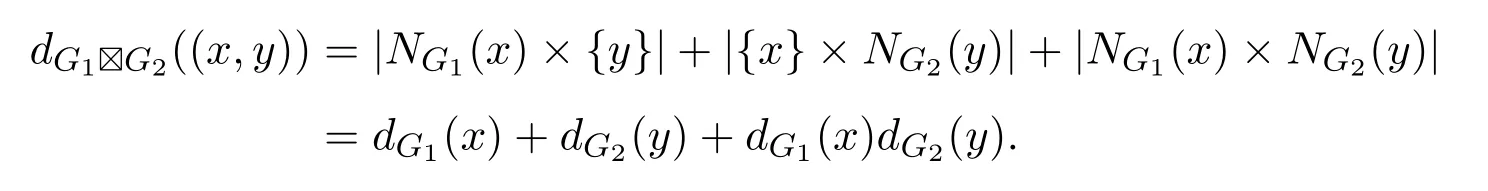
據(jù)此,在強(qiáng)乘積圖G1G2中有且僅有如下2k個(gè)度數(shù)為奇數(shù)的頂點(diǎn):

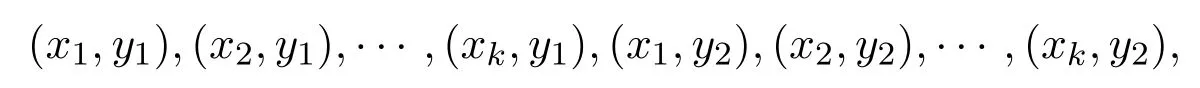
在G1G2中添加連接頂點(diǎn) (xi,y1)和 (xi,y2)的新邊ei(i=1,2,···,k),所得到新的連通圖記為 (G1G2)?,即

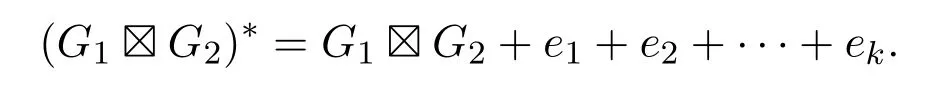
設(shè)T是圖(G1G2)?中最長(zhǎng)的跡,記為

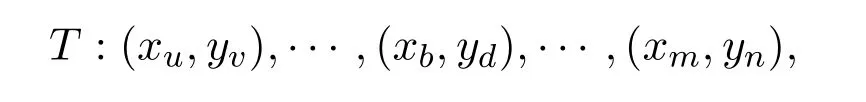
可以斷言(xu,yv)=(xm,yn).若不然,跡T終止于(xm,yn)(xu,yv).根據(jù)強(qiáng)乘積的定義,頂點(diǎn)(xm,yn)可能作為T的內(nèi)部頂點(diǎn)已經(jīng)在終點(diǎn)前出現(xiàn)過,并且每出現(xiàn)一次都有(G1G2)?中的兩條邊與之關(guān)聯(lián).又因?yàn)門終止于頂點(diǎn)(xm,yn),所以就有奇數(shù)條邊與頂點(diǎn)(xm,yn)關(guān)聯(lián).根據(jù)(G1G2)?的構(gòu)造方法,可知(G1G2)?中每個(gè)頂點(diǎn)的度數(shù)都是偶數(shù).由此可知頂點(diǎn)(xm,yn)至少還關(guān)聯(lián)著一條不在T中的邊,設(shè)該邊為e′,那么可以得到 (G1G2)?的一條跡T+e′,這矛盾于T是最長(zhǎng)跡.因此圖 (G1G2)?的最長(zhǎng)跡T是一條閉跡.這里將證明:圖(G1G2)?的最長(zhǎng)閉跡T包含其所有的邊,即T是 (G1G2)?的一個(gè) Euler環(huán)游.假設(shè)不然,T未包含圖(G1G2)?的所有的邊.因?yàn)?(G1G2)?是連通的,所以對(duì)于T中的某頂點(diǎn) (xb,yd),一定存在著一條不在T中的邊e′與它關(guān)聯(lián).設(shè)H=(G1G2)??E(T),取圖H中包含邊e′的連通分支H1,H1是非平凡且連通的.因?yàn)殚]跡T中的每個(gè)頂點(diǎn)關(guān)聯(lián)(G1G2)?的偶數(shù)條邊,所以圖H的每個(gè)頂點(diǎn)的度數(shù)為偶數(shù),也說明了連通分支H1的每個(gè)頂點(diǎn)度為偶數(shù).現(xiàn)考慮H1中起始于頂點(diǎn)(xb,yd)的一條最長(zhǎng)跡,根據(jù)上述討論,這條最長(zhǎng)跡必須終止于頂點(diǎn) (xb,yd),記這條閉跡為T′.此時(shí),在跡T到達(dá)頂點(diǎn) (xb,yd)時(shí),把T′粘到T上,從而可獲得(G1G2)?中一個(gè)比T更長(zhǎng)的跡,這導(dǎo)致矛盾.故圖(G1G2)?的最長(zhǎng)閉跡T包含其所有的邊,即T是(G1G2)?的一個(gè)Euler環(huán)游.接下來,從T中刪除連接 (xi,y1)和 (xi,y2)的邊ei(i=1,2,···,k),即T?e1?e2?···?ek,可以得到強(qiáng)乘積圖G1G2中k=|V(G1)|條邊不交的跡T1,T2,···,Tk,使得

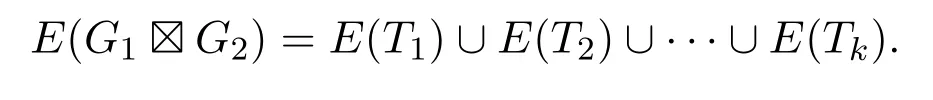
本定理得證.

定理 2.3設(shè)G1和G2是兩個(gè)連通圖.強(qiáng)乘積圖G1G2含有一條Euler通路當(dāng)且僅當(dāng)G1和G2之一是平凡圖,而另一個(gè)恰有兩個(gè)度數(shù)為奇數(shù)的頂點(diǎn).

證明設(shè)圖G1和G2之一是平凡圖,而另一個(gè)恰有兩個(gè)度數(shù)為奇數(shù)的頂點(diǎn),根據(jù)定理2.2,可知強(qiáng)乘積圖G1G2含有一條Euler通路.

反之,設(shè)強(qiáng)乘積圖G1G2的Euler通路為L(zhǎng),記為

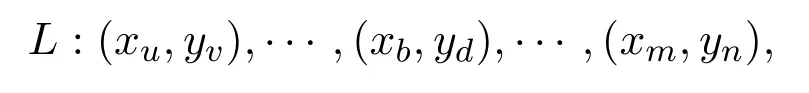
頂點(diǎn)(xb,yd)作為L(zhǎng)的內(nèi)部頂點(diǎn)每出現(xiàn)一次,就會(huì)有G1G2中的兩條邊與之關(guān)聯(lián).因?yàn)镋uler通路L包含了強(qiáng)乘積圖G1G2中所有的邊,所以對(duì)于所有不同于起點(diǎn)和終點(diǎn)的內(nèi)部頂點(diǎn),它們的度數(shù)為偶數(shù).又因?yàn)長(zhǎng)起始于頂點(diǎn) (xu,yv)且終止于頂點(diǎn)(xm,yn),所以起點(diǎn)(xu,yv)和終點(diǎn)(xm,yn)的度數(shù)為奇數(shù).根據(jù)強(qiáng)乘積的定義,有

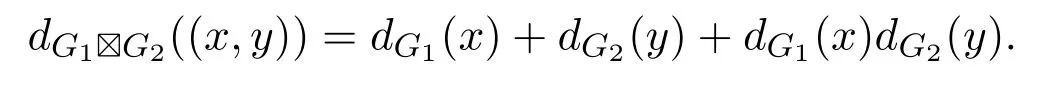
因?yàn)?xu,yv)的度數(shù)為奇數(shù),所以xu和yv中至少有一個(gè)頂點(diǎn)度數(shù)為奇數(shù).不妨設(shè)頂點(diǎn)xu的度數(shù)為奇數(shù),那么頂點(diǎn)(xu,yn)的度數(shù)也為奇數(shù).因?yàn)閺?qiáng)乘積圖G1G2僅有起點(diǎn)(xu,yv)和終點(diǎn)(xm,yn)的度數(shù)為奇數(shù)并且它們是不同的頂點(diǎn),所以可以得到下面兩種情況:(1)yn=yv且xuxm;(2)xu=xm且ynyv.由于無向圖中度數(shù)為奇數(shù)的頂點(diǎn)有偶數(shù)個(gè),若xu=xm,則在Euler通路L中必然存在著不同于起點(diǎn)和終點(diǎn)且度數(shù)為奇數(shù)的頂點(diǎn),導(dǎo)致矛盾.因此可以得到只有(1)成立,即yn=yv且xuxm.對(duì)于L中不同于起點(diǎn)和終點(diǎn)的任意內(nèi)部頂點(diǎn)(xb,yd),可以斷言yd=yn=yv和頂點(diǎn)xb的度數(shù)為偶數(shù).如若不然,(xu,yb)和(xm,yb)或者(xb,yd)為L(zhǎng)中不同于起點(diǎn)和終點(diǎn)且度數(shù)為奇數(shù)的內(nèi)部頂點(diǎn),導(dǎo)致矛盾.綜上可以得到,G2是平凡圖且G1恰有兩個(gè)度數(shù)為奇數(shù)的頂點(diǎn).同理,不妨設(shè)頂點(diǎn)yn的度數(shù)為奇數(shù).利用上述相似方法,可以得到G1是平凡圖且G2恰有兩個(gè)度數(shù)為奇數(shù)的頂點(diǎn).

3 結(jié)論

強(qiáng)乘積是通過若干特定的階數(shù)較小的圖來構(gòu)造大圖的有效方法,也是一種設(shè)計(jì)大規(guī)模互連網(wǎng)絡(luò)的重要方法.本文研究強(qiáng)乘積圖的Euler跡問題,給出了強(qiáng)乘積圖是Euler圖的充分必要條件和強(qiáng)乘積圖含有Euler通路的充分必要條件.