基于位移的鋼筋混凝土框架結構整體等效阻尼比模型

閆路路，馮治斌，貢金鑫

(大連理工大學 土木工程學院；海岸和近海工程國家重點實驗室，遼寧 大連 116024)

基于位移的抗震設計方法是近年來結構抗震設計發展的一個重要方向，相比于傳統基于力的抗震設計方法，基于位移的抗震設計方法[1-3]不僅考慮了結構在正常使用條件下的承載能力，還考慮了強震下結構屈服后的能力，從而可從多方面對結構抗震性能進行有效控制。等效線性化方法作為一種基于靜力非線性分析確定結構位移需求的簡化方法，已廣泛應用于結構性能分析與位移設計中。該方法的核心是通過構造一個與非線性結構等效的線性體系，計算結構的最大位移，等效周期和等效阻尼比作為其中的關鍵參數，其取值的合理性將直接影響結構抗震分析和設計的可靠性。

學者們很早就開展了等效周期和等效阻尼比的相關研究[4-14]，研究方法可分為3類：解析方法、經驗方法和試驗分析方法。在解析方法中[4-7]，等效周期早期采用結構的初始周期，后來采用Rosenbluenth等[4]建議的按最大位移處割線剛度計算的周期，等效阻尼比采用Jacobsen[5]提出的等能量耗散原則，根據結構的滯回耗能進行確定；經驗方法[8-11]主要基于動力時程分析結果與等效線性化分析結果的誤差最小化原則，通過擬合分析獲取結構的等效周期和等效阻尼比；試驗方法[12]主要通過分析結構或構件振動臺試驗結果，并依據能量平衡原則計算等效參數，但由于實驗所用的結構或構件樣本數量較少，其計算結果的適用性依然有待進一步明確。

對于鋼筋混凝土框架結構，當前已有的等效阻尼比模型大多通過將結構等效為單自由度體系并利用Takeda滯回模型或與之類似的滯回模型推導得出[1]。然而，Takeda滯回模型是通過鋼筋混凝土柱的擬靜力實驗發展而來的[15]，對于單個構件或橋梁等類型的結構適用性較好，而在框架結構中，由于各構件在軸壓比、配筋率等方面存在差異，不同構件適用的滯回參數并不相同。同時，抗震規范從能力保護的角度要求實現強柱弱梁，即塑性鉸盡可能出現在梁端和底層柱底。由此可見，地震作用下框架結構的整體滯回耗能行為通常較為復雜，使用由構件滯回模型推導得到的等效阻尼比近似反映實際結構的整體滯回特性并不十分合理，故有必要直接從多自由度鋼筋混凝土框架結構本身出發并考慮其變形機制，確定結構的整體等效阻尼比模型。

首先，采用PKPM軟件，按現行抗震設計規范設計了66個不同層數、跨度和設防烈度的規則鋼筋混凝土框架結構；然后，采用Opensees軟件對結構進行單向推覆(Pushover)分析，挑選出其中符合性能設計所要求的塑性鉸分布結構(即主要通過梁端和底層柱腳處的塑性鉸進行滯回耗能的結構，分析表明，按現行規范設計的框架，塑性鉸并不一定只出現在梁端和底層柱腳)，再對這些結構進行不同位移幅值下的往復推覆分析，根據結構滯回環的面積，采用Jacobsen方法確定結構整體等效阻尼比；最后，以彈塑性動力時程分析結果為基準對該等效阻尼比進行修正，使擬靜力非線性分析結果與彈塑性時程分析結果的均值保持一致，并與已有的等效阻尼比模型進行了對比。

1 分析采用的鋼筋混凝土框架結構

1.1 結構模型

為了確定多自由度鋼筋混凝土框架結構的等效阻尼比模型，綜合考慮結構布置和設計參數對結構整體滯回特征的影響，設計了66個符合《建筑抗震設計規范》(GB 500011—2010)[16]的規則鋼筋混凝土框架結構，表1給出了這些結構的基本信息。所有結構的橫向(X)和縱向(Y)均為三跨，底層層高均為4.5 m，其他樓層層高均為4 m。按照平面尺寸將結構分為兩組，每組33個結構，如表1所示。第1組結構(編號1～33)的橫向(X)和縱向(Y)跨度均為6 m；第2組結構(編號34～66)的橫向(X)跨度為9 m，縱向(Y)跨度為6 m。每組結構考慮4個不同的設防烈度(7度(0.1g)、7度(0.15g)、8度(0.2g)、8度(0.3g))，每個設防烈度下均包含若干不同層數的結構，其中，最低層數為3，最高層數依據《高層建筑混凝土結構技術規程》(JGJ 3—2010)[17]確定。所研究模型的跨度參考《建筑模數協調標準》(GB 50002—2013)確定，此外，模型的平立面布置方式及跨數參考文獻[18]確定。根據該文獻可知，表1所列模型能夠包含典型規則鋼筋混凝土框架結構體系的主要結構構件并考慮其基本受力特征。所有結構的場地類別均按Ⅱ類考慮，設計地震分組為第1組，柱混凝土強度等級為C35，梁和板均為C30，縱筋使用HRB400鋼筋。樓面活荷載為2.0 kN/m2，附加恒荷載為2.5 kN/m2，梁上恒荷載為5 kN/m；屋面活荷載為0.5 kN/m2，附加恒荷載為4.0 kN/m2。樓板厚均為150 mm，各結構梁柱截面尺寸根據結構跨度、層高等幾何條件以及規范中的軸壓比限值要求、配筋率要求、變形要求等設計條件綜合確定，構件配筋借助PKPM結構設計軟件確定，表2以15號結構為例，給出了其截面尺寸及配筋信息。

表1 結構模型Table 1 Characteristic of studied structures

表2 15號結構的截面及配筋信息Table 2 Information of cross section and reinforcement for the structure with No.15

采用有限元軟件OpenSees對表1中的結構進行非線性分析。由于所選結構的平面、立面布置較為規則，為簡化分析，僅從結構的X方向取中間一榀進行計算。結構模型的建立過程主要考慮主梁、柱等抗側力構件，且不考慮樓板對梁的影響；對于填充墻等非結構構件及次梁等非抗側構件，則僅考慮其對結構自重的影響，而不考慮對結構整體滯回特性的影響。梁柱構件均使用纖維單元模擬，其中，混凝土纖維使用Concrete02材料模型，鋼筋纖維使用Steel02材料模型。此外，采用Zhao等[19]建議的方法，在梁端附加零長度單元，以模擬梁端縱筋粘結滑移的影響，使用Pinching4本構模型模擬其滯回行為[20-21]，相關模型參數依據文獻[22]確定。

1.2 結構變形模式

對表1中的框架結構進行單向推覆分析。考慮到地震作用下結構的位移反應主要由第一振型控制，使用式(1)的側向荷載分布模式進行推覆。

(1)

式中：mi和mj分別為第i層和第j層的質量；φ1,i和φ1,j分別為結構第一振型向量在第i層和第j層的分量；n為結構的總層數；V為結構的基底剪力。

依據推覆分析得到的結構塑性鉸分布情況，可將結構變形模式分為梁鉸變形模式、柱鉸變形模式和混合鉸變形模式。對于框架結構，通常難以完全避免柱端塑性鉸的出現，但當柱鉸的數量較少且塑性發展程度較弱時，其對整體結構失效機制的影響較小，結構依然以梁鉸變形耗散地震能量為主，從而具有較好的延性變形能力和滯回耗能能力[23]。

表3統計了最大層間位移角為0.02時各結構的塑性鉸機制，其中，0.02對應于中國抗震規范規定的大震下框架結構層間位移角限值。圖1分別以17、34、15、54號結構為例給出了塑性鉸分布圖，其中，塑性鉸的性能狀態參考文獻[24]的方法確定，可以看出，圖1(a)結構為梁鉸模式，圖1(b)結構為柱鉸模式，圖1(c)、(d)結構均為混合鉸模式，其中，圖1(c)中的柱鉸(除柱底外)均處于立即使用狀態，塑性變形程度較輕。對混合鉸結構進行進一步區分，將柱端塑性變形不超過“立即使用”性能水平、出現塑性變形的柱不超過其所在樓層柱總數量50%的結構(如圖1(c)所示)判定為柱端塑性程度較輕的混合鉸結構。在后面確定結構整體等效阻尼比時，僅選取其中出現梁鉸變形機制的結構和柱端塑性變形程度較輕的混合鉸變形機制的結構進行分析，所選結構具備性能化抗震所要求的耗能機制，從而可使所提出的等效阻尼比模型滿足性能化設計需求，共選取51個結構。

表3 66個結構的破壞機制Table 3 Deformation mechanisms of the 66 frame structures

圖1 結構的塑性鉸模式Fig.1 The plastic hinge mechanism of

2 結構整體等效阻尼比

2.1 基于等能量原則的等效阻尼比

對表3中選取的51個符合抗震耗能要求的結構進行往復推覆分析，分析時使用變幅加載方式，即位移循環的幅值逐級增加，且每級荷載往復1次，最終可得到不同位移幅值下的結構基底剪力-頂點位移滯回環。圖2(a)所示為結構在一個位移循環下的典型滯回環，參考文獻[12]可知，根據Jacobsen所提出的等能量耗散原則，結構在一個位移循環下的滯回耗能應等于相應位移循環下等效線性結構的粘滯阻尼耗能(如圖2(b)所示)，此時，結構的等效阻尼比為

ζeff=ζvis+ζhys

(2)

式中：ζvis為結構的彈性粘滯阻尼比，鋼筋混凝土結構一般取0.05；ζhys為結構的等效滯回阻尼比，可按式(3)確定。

(3)

式中：Ehys為圖2(a)中ABCD面積，代表結構的滯回耗能；Eso為等效線性體系的彈性變形能，等于圖2(b)中三角形OAE的面積，按式(4)計算。

(4)

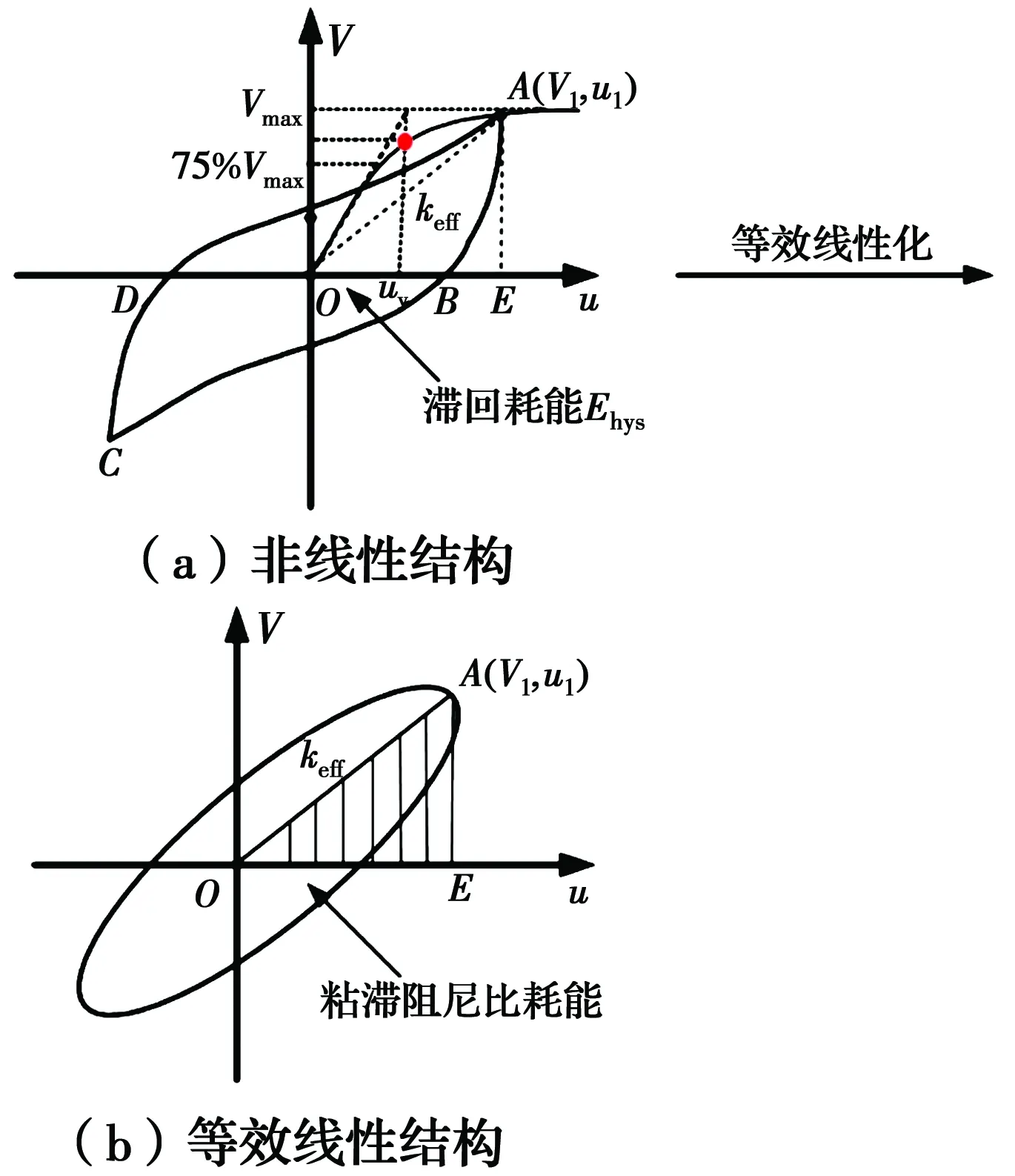
圖2 非線性結構基于Jacobsen方法[12]的等效線性化

后文分析中需確定不同位移幅值對應的延性系數，而結構Pushover曲線通常是一條光滑的曲線，為此，使用Park方法[25]確定結構的屈服點，如圖2(a)所示，圖中uy代表屈服位移。

圖3(a)～(d)以編號為7、23、42和58的結構為例，給出了結構在往復推覆下的基底剪力-頂點位移滯回曲線。可以看出，各結構的滯回環形狀是相似的，且均近似關于原點反對稱。

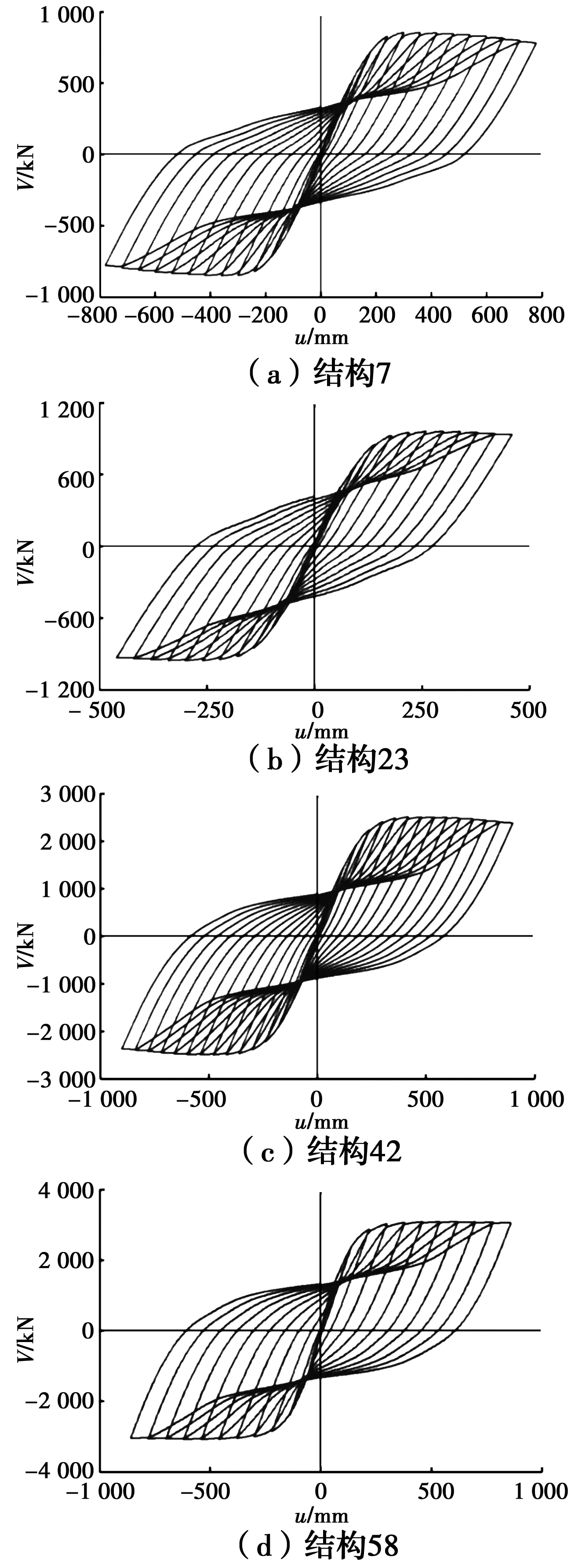
圖3 鋼筋混凝土框架結構的滯回曲線Fig.3 Cyclic pushover curves of RC frame

計算表3中選取的51個結構在不同位移幅值下的滯回環所包圍面積，得到對應的結構整體滯回耗能Ehys，進一步計算彈性變形能Eso，即可由式(2)得到不同延性系數μ對應的等效阻尼比，其中，延性系數根據位移幅值使用式μ=u/uy進行計算。表4給出編號為7和43結構在不同位移幅值下對應的滯回耗能Ehys、彈性變形能Eso、等效阻尼比ζeff和延性系數μ的計算結果。

圖4給出了表3所選51個結構等效阻尼比ζeff與延性系數μ的關系散點圖，對圖4中的數據進行回歸分析，得到鋼筋混凝土框架結構基于等能量原則的整體等效阻尼比公式。

ζeff=0.05+0.124(μ-1)0.5

(5)

2.2 等效阻尼比的修正

已有對單自由度體系等效阻尼比的相關研究[26-27]表明，采用基于Jacobsen等能量原則提出的等效阻尼比進行擬靜力非線性分析時，得到的結構最大位移與動力時程分析得到的結果通常有一定差別。例如，Dwairi等[26]對4種不同單自由度滯回模

表4 結構7和43在不同位移幅值下對應的Ehys、Eso、ζeff和μTable 4 The results of Ehys, Eso,ζeff and μ corresponding to different displacement for Structure No.7 and 43

圖4 等效阻尼比ζeff與延性系數μ的關系 Fig.4 Relationship between ζeff and

型的分析表明：在中長周期范圍內，與彈塑性動力時程分析得到的最大位移相比，采用基于等能量原則的等效阻尼比進行擬靜力非線性分析得到的位移偏低，即等效阻尼比偏大；在周期較短時，采用基于等能量原則的等效阻尼比計算得到的位移偏高，即等效阻尼比偏小。因此，Priestley等[12]建議應使用動力時程分析結果對基于能量相等原則提出的等效阻尼比進行修正，以提高其準確性。

為研究采用式(5)進行擬靜力非線性分析得到的結構最大位移與彈塑性時程分析結果的偏差，使用程玲[28]從美國太平洋地震工程研究中心(PEER)強震數據庫里選取250條地震記錄。地震波的選取不考慮近場地，以地面峰值加速度ag作為強度指標，將所選地震波分別調幅至0.3g～0.8g，間隔為0.1g，并對表3中選出的51個結構進行彈塑性動力時程分析，得到其最大頂點位移，隨后采用擬靜力非線性分析常用的能力譜法，根據式(5)所得等效阻尼比，計算不同地震強度下結構的目標位移，并將兩種方法計算結果進行對比。需要說明的是，擬靜力非線性分析與彈塑性動力時程分析結果的比較應以相同的地震作用為前提，為此，基于所選250條地震記錄的平均反應譜，確定擬靜力分析所需的需求譜，圖5所示為不同阻尼比下的平均偽加速度反應譜，式(6)為其擬合表達式[28]。

圖5 不同阻尼比下的加速度反應譜Fig.5 Response spectra with different damping

(6)

式中：η為阻尼比修正系數，其計算表達式為η=0.366 1ζ-0.336，其中ζ代表阻尼比。

圖6 基于式(5)等效阻尼比所得位移up1與動力時程分析結果的對比Fig.6 Comparison between up1 obtained by Eq. (5) equivalent damping ratio and

以彈塑性動力時程分析得到的平均最大位移為基準，為使擬靜力非線性分析得到的位移與彈塑性動力時程分析的平均最大位移一致，將式(5)修正為

ζeff=ζvis+κζhys=0.05+κ×0.124×(μ-1)0.5

(7)

式中：κ為修正系數，根據表3中所選的51個結構，按下列步驟確定：

1)從表3中選取一個結構，并依據式(1)的加載模式進行Pushover分析，得到該結構的基底剪力-頂點位移曲線。

2)利用式(8)分別計算結構的振型參與系數γ1和等效質量m，將步驟1)所得結構Pushover曲線(V-u關系)轉換為等效單自由度的力-位移關系(f-x關系)，并進一步計算屈服位移xy。

(8)

式中：φ1為結構的第一振型向量；M為結構的質量矩陣；l為影響系數向量；f和x分別代表等效單自由度體系的力和位移。

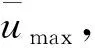
4)利用式(8)將up轉換為等效單自由度結構的目標位移xp，并由式(9)計算對應的延性系數μ、等效剛度keff、等效周期Teff和譜加速度Sa。

(9)

式中：fp為步驟2)所得等效單自由度體系力-位移曲線上與目標位移xp對應的荷載值。

5)將步驟4)所得等效周期Teff和譜加速度Sa代入反應譜公式(6)中，計算修正后的等效阻尼比ζcor,eff。

6)將延性系數μ代入式(5)，計算對應的基于等能量方法的等效阻尼比ζeff。

7)將ζcor,eff和ζeff均減0.05(固有阻尼比ζvis)，得到對應的等效滯回阻尼比ζcor,hys和ζhys(參考式(2))，則修正系數κ可通過式(10)計算。

(10)

8)改變峰值地面加速度ag，重復步驟3)～7)，得到不同ag下的阻尼比修正系數κ。

9)從表3中另選結構，重復步驟1)～8)，得到不同結構的阻尼比修正系數κ。

圖7給出了表3中所選51個結構的阻尼比修正系數κ與結構周期T的關系。通過非線性擬合分析可得修正系數κ的表達式(式(11))。

κ=(T-1.2)2+0.70 (0.4≤T≤2.0)

(11)

圖7 κ與T的關系Fig.7 Relationship between κ and

將式(11)代入式(7)，即得到修正后的等效阻比表達式

ζeff=0.05+0.124×(μ-1)0.5×[(T-1.2)2+0.70]

(0.4≤T≤2.0)

(12)

由式(12)可以看出，修正后的等效阻尼比與結構基本周期有關。

為了驗證所提出等效阻尼比公式(12)的準確性，基于式(6)的反應譜，采用擬靜力非線性方法計算表3中所選51個結構在不同地震強度下的目標頂點位移，并將計算結果與彈塑性動力時程分析所得平均最大位移進行對比。圖8給出了兩種方法計算得到的位移對比結果。將圖8與圖6進行對比可以看出，采用式(12)的修正等效阻尼比進行擬靜力非線性分析得到的位移比基于式(5)等效阻尼比進行分析得到的位移更接近于彈塑性動力時程分析結果，說明采用修正的等效阻尼比模型能夠更準確地預測結構的最大位移響應。

圖8 使用修正后的等效阻尼比計算的up與的對比Fig.8 Comparison between up and

2.3 與已有等效阻尼比模型的對比

盡管前述中已經提到，現有的鋼筋混凝土結構等效阻尼比模型是基于單自由度結構得到的，且其與鋼筋混凝土框架結構的耗能機制也不完全相同，圖9將所提出的修正等效阻尼比模型與已有的5個等效阻尼比模型進行了對比，其中，所提出的模型僅給出T= 0.8 s時的情況。

圖9中Rosenblueth模型由雙線性滯回規則發展而來，滯回環較為飽滿，因而具有較高的等效阻尼比。ATC-40[29]采用Rosenblueth模型，并根據建筑物類型及新舊情況對其進行折減，圖9中ATC-40模型的曲線對應Type B建筑物的情況。圖中TT模型(Takeda thin)和TF模型(Takeda fat)均基于單自由度Takeda滯回模型得到，兩者的滯回參數不同[12]，TF模型的滯回環比TT模型的更為飽滿，因此，由TF模型得到的阻尼比較大。Gulkan模型[11]是通過縮尺鋼筋混凝土框架的振動臺試驗并依據能量平衡原則得到的等效阻尼比。總體來看，所提修正等效阻尼比模型的數值介于TF模型、TT模型和ATC-40模型之間。

圖9 不同等效阻尼比的對比Fig.9 Comparison of the equivalent damping

3 算例驗證

前文在分析時僅考慮了等跨的鋼筋混凝土框架結構，為進一步驗證所提等效阻尼比模型的適用性，設計了一個9層的不等跨鋼筋混凝土框架結構，圖10(a)、(b)分別給出了該結構的平立面布置。結構的抗震設防烈度為8度(0.2g)，場地類別為Ⅱ類，使用PKPM軟件對其進行配筋設計，各梁柱截面尺寸及配筋如圖10(c)所示。

圖10 框架結構布置圖及截面配筋Fig.10 Plan, elevation and member

為簡化計算，沿Y方向選取一榀框架建立有限元模型，并分別對其進行擬靜力非線性分析和動力時程分析，其中，擬靜力分析使用式(1)給出的側向荷載分布模式進行Pushover加載并使用所提修正等效阻尼比計算結構在不同地震強度下的目標位移，動力時程分析使用上文所選的250條地震記錄。表5分別給出了地面峰值加速度ag為0.3g、0.4g、0.5g和0.6g時，由動力時程分析計算得到的平均最大頂點位移和擬靜力非線性分析計算結果。可以看出，兩者總體上差異較小，在地震強度為0.3g時誤差最小，僅為0.65%。說明所提出的等效阻尼比可以較為準確地預測此類不等跨鋼筋混凝土框架結構在不同地震強度下的位移響應，具有較好的適用性。

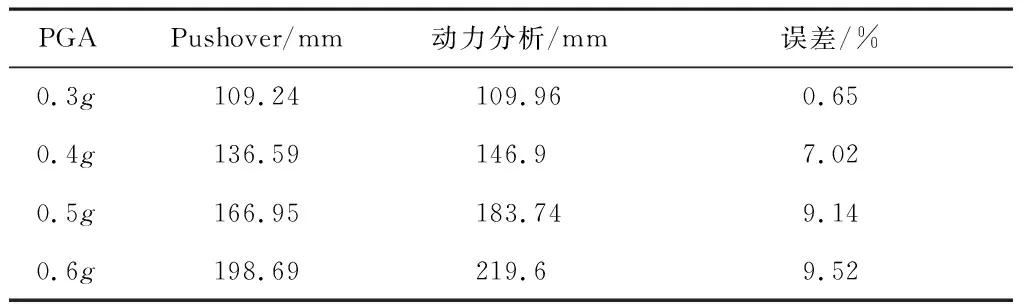
表5 計算結果對比Table 5 Comparison of results

4 結論

對符合抗震設計規范的66個鋼筋混凝土框架結構進行單向和往復推覆分析，建立了反映規則鋼筋混凝土框架結構實際變形和耗能特征的結構整體等效阻尼比模型，并通過彈塑性動力時程分析對等效阻尼比進行了修正。得出如下主要結論：

1)目前已有的結構等效阻尼比模型多是通過對單自由度體系進行分析得來，且采用的多是針對構件的滯回模型，不能反映鋼筋混凝土多層框架結構的耗能特點，即主要通過梁端和柱底塑性鉸的塑性變形耗能。

2)在地震作用下，按現行抗震規范設計的鋼筋混凝土框架結構大部分結構塑性鉸主要出現在梁端，但有少部分結構出現了明顯的柱鉸變形機制。在建立結構整體等效阻尼比模型時，去除了其中耗能能力較差的結構，主要針對能夠滿足性能化設計要求的鋼筋混凝土框架結構。

3)采用基于等能量原則建立的等效阻尼比模型進行擬靜力非線性分析時，得到的結構最大位移通常與彈塑性動力時程分析所得平均最大位移有一定差異，需進一步以動力時程分析結果為基準對其進行修正，修正后的等效阻尼比可較為準確地預測結構在不同地震強度下的位移需求。