基于羅德里格矩陣的點云初始配準研究

邢 正 全

(山東電力工程咨詢院有限公司，山東 濟南 250100)

1 概述

三維激光掃描技術依靠其非接觸、實時、動態、高精度等傳統測量方式所不具備的獨特優勢，提供了一種全新的數據獲取方式，在測繪領域，被認為是繼GPS技術以來的又一次技術革新，也正在被越來越廣泛的得以應用。受掃描物體、掃描儀本身及周圍環境的影響，往往需要多次設站才能獲得物體的完整信息，不同設站獲得的點云數據都是基于掃描儀獨立坐標系下的數據，將不同測站下的點云數據統一到相同的坐標系下，即是點云配準。

將不同測站下的點云數據統一到一個坐標系內，可以通過坐標系的轉換來完成。常用的空間直角坐標系轉換模型如布爾沙模型，莫洛金斯模型和武測模型等主要為小角度轉換模型[1]，而實際點云坐標轉換中，3個歐拉角往往為任意大小，此時應采用嚴密的大旋轉角空間直角坐標轉換模型。文獻[4]采用羅德里格矩陣進行坐標轉換，取得了較好的效果。考慮到可以在兩測站點云數據中獲得不同組近似同名點對，因此本文在文獻[4]的基礎上，將羅德里格矩陣引入到解算轉換模型中，實現兩測站點云的粗配準。

2 點云數據配準模型

根據文獻[2]，點云坐標轉換的大旋轉角7獨立參數模型為：

(1)

模型包含3個平移參數X0,Y0,Z0,1個尺度參數μ和3個大角度旋轉參數A,B,C，通過該轉換模型可以將旋轉系O-xyz中的三維激光掃描數據點坐標(x,y,z)轉換到參考系O-XYZ中。

這里，三維旋轉矩陣的一種具體形式如下：

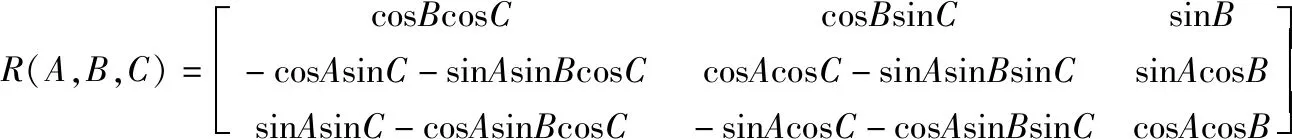
(2)

用方向余弦表示即：

(3)

用級數展開13個參數得到線性轉換模型的誤差方程式：

(4)

式中:

Vi=[VXiVYiVZi]T。

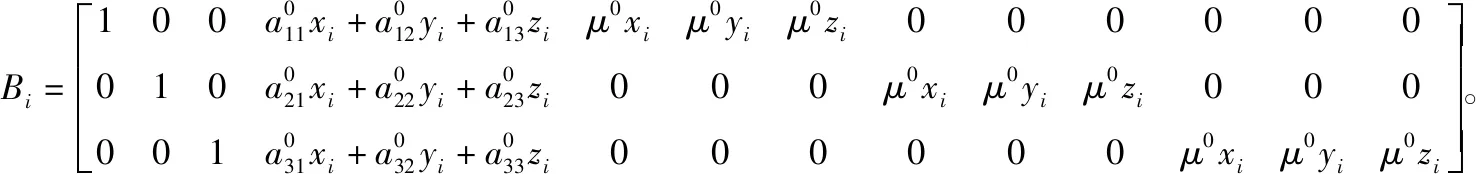
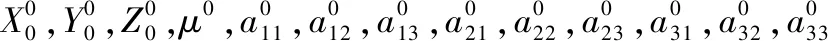
3 基本原理

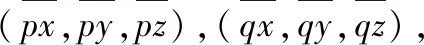
(5)

其中，m為兩幅點云各自包含的點的個數。

將重心化之后的同名點對坐標代入式(1)可以得到：

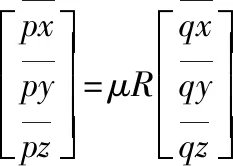
(6)

(7)

因此，變換參數可以根據式(6),式(7)分步來求解。

由于實驗數據是由同一臺三維激光掃描儀采集得到的，所以在配準轉換的過程中可以不考慮尺度變換的影響，那么模型中μ=1。引入反對稱矩陣S如下：

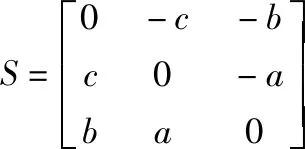
(8)

其中，元素a,b,c是獨立的，旋轉矩陣R可以表示為以下形式：

R=(I-S)-1(I+S)

(9)

其中，I為3階單位矩陣。

將式(8),式(9)代入式(6)展開整理可得：

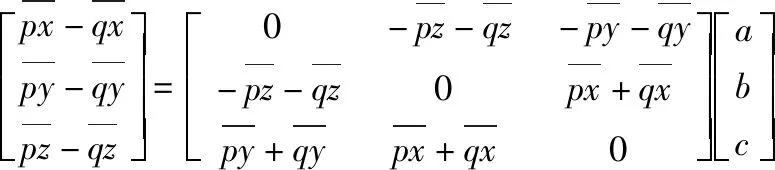
(10)

因此，如果有n組同名點對，就可根據式(10)列出如下誤差方程：

V3n×3=B3n×3X3×1-L3n×1

(11)

其中，X3×1=[abc]T。

利用式(11)，根據最小二乘原理，無需迭代就可以直接求得羅德里格參數：

(12)

然后由式(9)即可求得旋轉矩陣R，進一步可由式(7)求得平移矩陣T。將變換參數(R,T)應用于目標點集就實現了參考點集與目標點集的配準。

4 實驗分析

采用三維激光掃描儀掃描某建筑物，獨立設站獲得2組點云數據。令它們分別為CZ1和CZ2，原始點云如圖1所示。

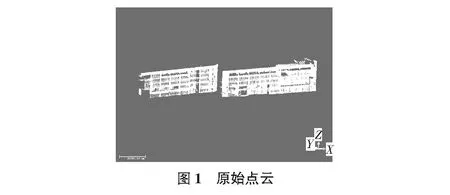
為了利用羅德里格矩陣進行粗配準，首先在兩站點云的重疊區域選取近似的同名點對，這里選取6對同名點對，它們在各自測站中的坐標如表1所示。

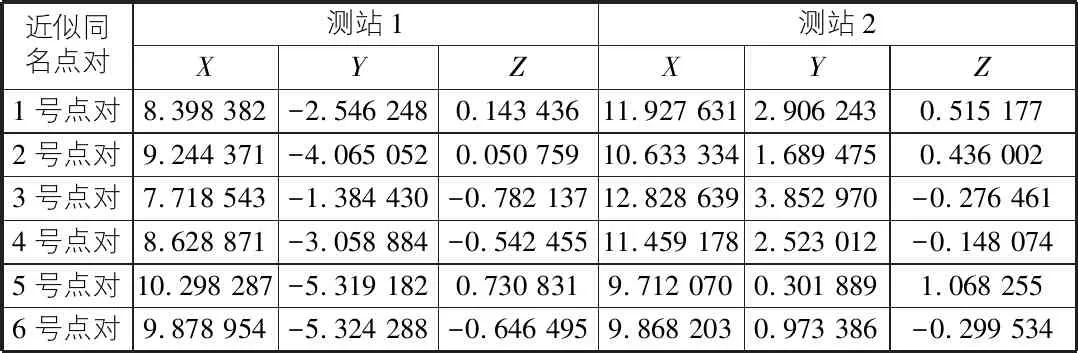
表1 選取的近似同名點對坐標信息

根據以上6對近似同名點對，按照以上羅德里格矩陣的方法求得旋轉矩陣和平移矩陣分別為：

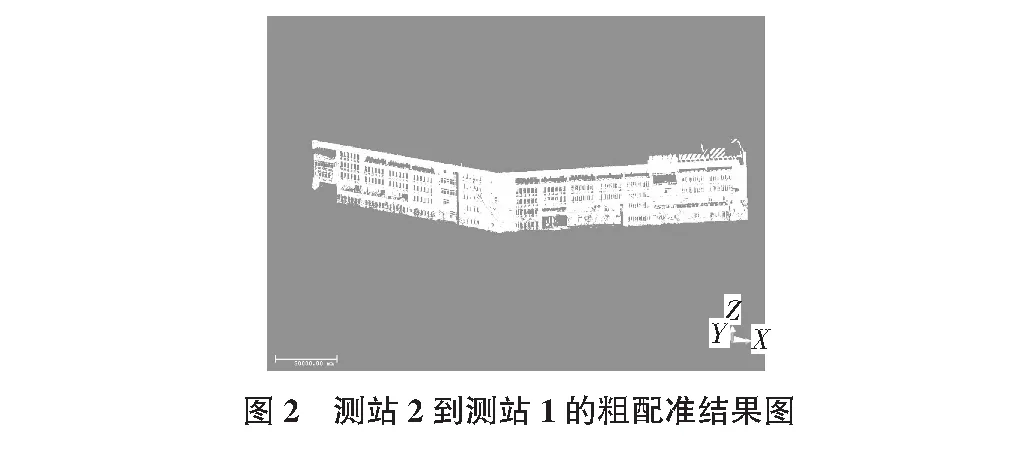
將R,T應用于測站2數據，實現測站2到測站1的粗配準，結果如圖2所示。

5 結語

從配準結果可以看出，該方法實現了較好的粗配準效果，另外，該方法計算速度快，易于編程實現且不受旋轉角大小的限制，方法具有很好的適用性，所以應用羅德里格矩陣進行坐標轉換求解以實現點云粗配準的方法是可行的。