預緊力對滾柱直線導軌副剛度特性影響的研究

宋現春樊明貞王皓陳洪建榮伯松

(1.山東建筑大學 機電工程學院，山東 濟南250101；2.山東博特精工股份有限公司，山東濟寧272071)

0 引言

滾柱直線導軌副是數控機床的關鍵功能部件，其制造水平的高低在很大程度上影響了數控機床的發展。由于具有承載能力強、接觸剛度高、摩擦阻力小、精度保持性好等優點，眾多企業將其運用到工業生產中。

靜剛度表示滾柱直線導軌副在承受外載荷時抵抗變形的能力。疏亞雅[1]利用Hertz接觸理論分析了滾柱和滾道之間的受力關系，基于Palmgren公式建立了導軌副水平、垂直和繞主軸轉動等3個方向的剛度模型，并對其進行有限元分析，探究了預緊力及滑塊變形對靜剛度的影響，結合試驗數據分析得出，考慮群部變形所得靜剛度與試驗數據更接近；張巍等[2]運用齊次變換矩陣建立滾柱直線導軌副的剛度模型，分析了滾柱直線導軌副在不同預緊力和接觸角下彈性變形量，找到了滾柱直線導軌副不同預緊力和接觸角對其剛度特性的影響規律。

對導軌副動力學分析的關鍵在于對其結合面的動態特性研究。陳蓉等[3]基于ANSYS Workbench仿真軟件對不同預緊力下滾柱直線導軌副進行仿真分析，得到各階固有頻率及振型，并結合模態試驗，分析出不同預緊力對滾柱直線導軌副振動特性的影響規律。成建平等[4]利用彈簧單元代替結合面導軌與滑塊的接觸，采用Palmgren的經驗公式，通過等效法得到彈簧單元的等效剛度，并驗證了滾柱直線導軌副高剛度的特性。Shimizu[5]通過多滑塊結構為基礎，以變形協調關系為基礎建立整體剛度模型，假設基礎是以多滑塊剛度一致進行，但與實際情況契合度不高。Ohta等[6]發現滾動直線導軌副的實測靜剛度值遠小于理論計算值，其原因是導軌副預緊之后滑塊群部變形。還有學者對滾動直線導軌副的滾動體在承受偏載情況時，進行接觸力學分析，建立了剛度與負載之間的函數關系[7-8]。

預緊力對直線導軌副的動靜剛度有直接的影響研究，通常采用增大滾柱直徑的方法增加預緊力，從而提高導軌副的剛度和承載性能。文章通過建立滾柱直線導軌副剛度模型，研究預緊力對滾柱直線導軌副彈性變形量及固有頻率的影響，從而為研究其剛度特性提供依據。

1 滾柱直線導軌副的剛度特性研究方法

1.1 剛度特性的試驗測量方法

以濟寧博特精工股份有限公司的JSA-LZG45型滾柱直線導軌副為研究對象，該型號直線導軌副為四方向等載荷結構，相關參數見表1。

在結合面的基礎參數中，剛度主要影響結構系統的固有頻率和振動幅值，阻尼一般不影響系統固有頻率，且在靜力學分析中阻尼的存在并不影響分析結果。所以，在進行有限元建立模型時，采用等效法，將滑塊與導軌結合面之間的滾動體等效為若干彈簧單元連接滑塊和導軌，分別布置在4個滾道內滑塊長度的1/4、1/2、3/4處[9-11]，如圖1所示。

表1 JSA-LZG45型滾柱直線導軌副相關參數表

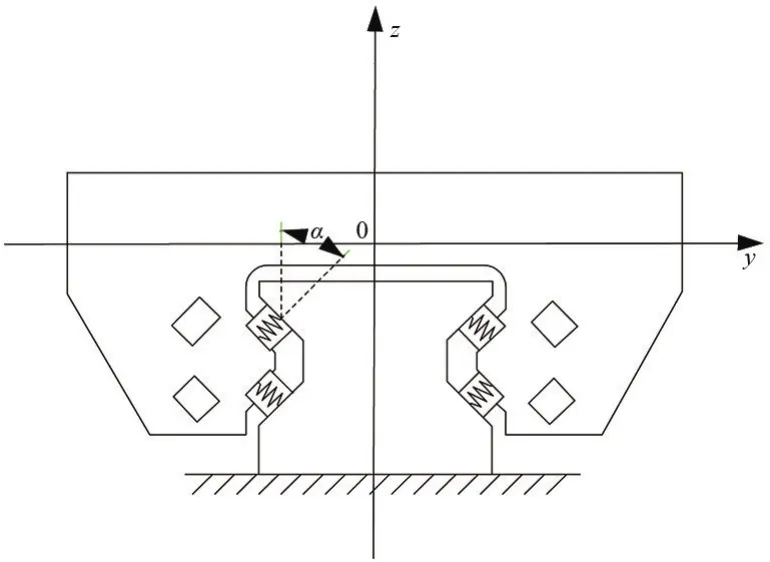
圖1 阻尼彈簧單元的剛度模型圖

靜剛度試驗采用滾動直線導軌副靜剛度試驗臺裝置進行試驗研究，如圖2所示。試驗臺是由機械主體、控制系統及測試系統組成的。機械主體主要包括床身、支撐立柱、被測導軌副、上橫梁、加載頭、滑塊夾具和導軌夾具體等；控制系統主要包括驅動控制系統、交流伺服電機和液壓比例加載系統等；測試系統主要包括稱重傳感器和位移傳感器。

圖2 滾動直線導軌副靜剛度試驗臺結構圖

試驗臺的主要功能是測量在垂直載荷下滾動直線導軌副的彈性變形量，在設計時應確定最大加載載荷(20%C)，可測導軌副的規格為35、45、55和65型滾柱直線導軌副。試驗臺采用液壓加載，加載方式主要有:(1)勻速施加，到達最大值后保持最大載荷一段時間，然后勻速卸載；(2)階梯式加載，按照最大加載力的百分比逐級加載，每階段勻速加載達到指定值后穩壓一段時間，直到加載力的最大設定值，然后以同樣的方式卸載。試驗采用階梯式加載，可實現直線導軌副液壓伺服的比例加載，加載力在0～100 kN連續可調，滿足試驗要求。

模態試驗所采用的滾柱直線導軌副的結構與有限元模型一致。采用DHL050型號的力錘傳感器對滑塊進行激振，采用INV9822A型號的加速度傳感器(適用測量頻率比較高的機械結構)拾振。信號采集儀是東方振動和噪聲技術研究所的INV3018C信號采集儀(8通道24位)，模態分析軟件采用的DASP V10模態分析軟件。現場裝置如圖3所示。

圖3 模態試驗測量裝置圖

錘擊法是現場試驗中應用較多的激勵方式，優點在于體積小、易攜帶，試驗的操作步驟簡單，測試速度快，力錘產生的能量比較分散。由于LZG45型滾柱直線導軌副的結構較小、質量較輕，所以應盡量減小其附加質量及其影響。因此，在模態試驗激勵時采用多點激勵單點輸出的方式進行測量，傳感器固定位置不變，力錘敲擊所有的測點，并且在力錘敲擊時應注意脈沖為單脈沖，避免試件與力錘的回擊。

1.2 受垂直載荷時接觸剛度計算

1.2.1 無預緊力時彈簧剛度計算

由于滾柱直線導軌副為四方向等載荷型結構，當滑塊受到不同方向的載荷時，導軌副中總有2列滾柱承受外部載荷。每個滾柱在外部載荷的作用下與導軌、滑塊分別構成一個接觸副，所有接觸副將產生彈性變形，從而使導軌副在力的方向上產生位移量[12-14]。采用Palmgren的經驗公式計算得到每個滾柱的接觸剛度，從而得到彈簧單元的等效剛度。

在垂直載荷F作用下，直線導軌副的i1、i2、i3、i4列滾柱中，只有i1、i2列滾柱承受載荷[15]，且每列滾柱承受的法向力為F′n，受力情況如圖4所示。

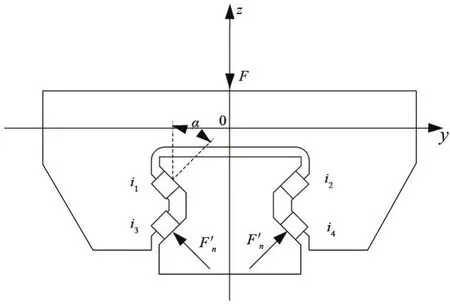
圖4 受垂直載荷時滾柱直線導軌副受力圖

每個滾柱受法向力F′n由式(1)表示為

式中:a為單列承載滾柱個數；α為接觸角，°；F為垂直載荷，N。

由Palmgren的經驗公式[16-17]，可求得每個接觸副的法向變形量δn，由式(2)表示為

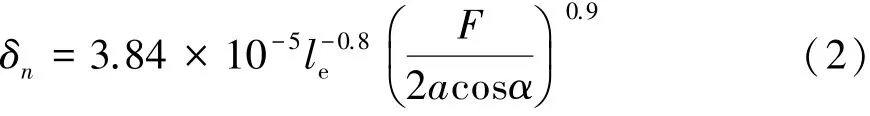
式中:le為滾柱與滾道的有效接觸長度，mm。

由于每個滾柱同時與滑塊和導軌構成接觸副，且其在每個接觸副的法向位移將導致導軌副在垂直方向上的位移，所以導軌副垂直方向的位移量δv由式(3)表示為

單個滾柱的接觸剛度Kc由式(4)表示為

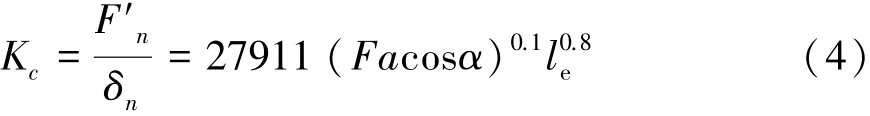
由于每個滾珠有2個接觸副，所以每根模擬彈簧剛度Ks由式(5)表示為

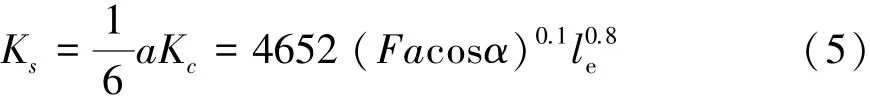
1.2.2 有預緊力時彈簧剛度計算

為了增加滾柱直線導軌副的剛度及運動時的精度，采用增大滾柱直徑的方法來施加預緊力。導軌副在垂直方向的彈性位移量δ0由式(6)表示為

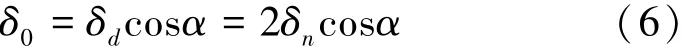
式中:δd為滾柱直徑過盈量，mm。

i1、i2列滾柱產生的豎直方向作用力為F1，i3、i4列滾柱產生的豎直方向作用力為F2，由式(7)和(8)表示為

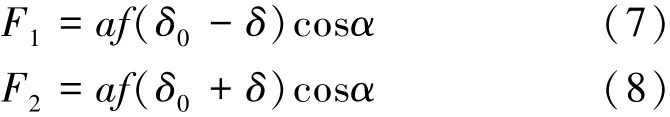
式中:δ為滾柱直線導軌副受垂直載荷時產生的彈性位移量，mm。

則求得垂直外載荷F由式(9)表示為

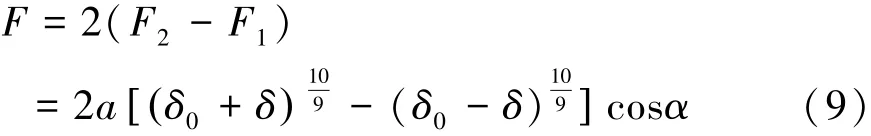
滾柱直線導軌副有預緊力時，求其靜剛度要以i1、i2列滾柱剛剛失去預緊力時導軌副產生的垂直位移量來計算[18-19]，即i1、i2列滾柱與滑塊脫離接觸，此時δ=δ0，則F1=0，總的外載荷F由式(10)表示為

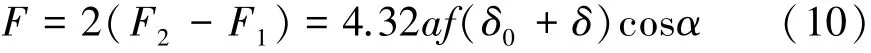
所以，當導軌副受預緊力時，每根模擬彈簧的剛度由式(11)表示為

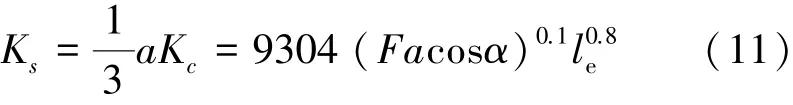
2 仿真結果分析

2.1 預緊力對垂直靜剛度的影響

通過ANSYS Workbench仿真分析，得到不同預緊力對直線導軌垂直剛度的影響。分別取0.01C、0.05C和0.1C不同等級預緊力，在滑塊上分別施加2、4、6、8、10、12、14 kN 的垂直載荷，導軌副的變形量見表2。

表2 不同預緊力下直線導軌副的變形量表

將垂直外載荷與導軌副變形量之間的關系轉換為剛度曲線，如圖5所示。無預緊力時，導軌副剛度為1 385.7 N/μm，輕預緊力時導軌副剛度為2 482.3 N/μm，中預緊力時導軌副剛度為2 713.2 N/μm，重預緊力時導軌副剛度為2 816.9 N/μm，因此，對滾柱直線導軌副施加預緊力可以顯著提高導軌副的剛度。當施加輕預緊力時，剛度曲線斜率是無預緊力時曲線斜率的1.8倍，導軌副的剛度變化明顯增大，繼續增大預緊力時，剛度變化減小。同時，預緊力過大會加大導軌副的磨損，降低其的運行精度和工作壽命。因此，合理施加預緊力對導軌十分重要。

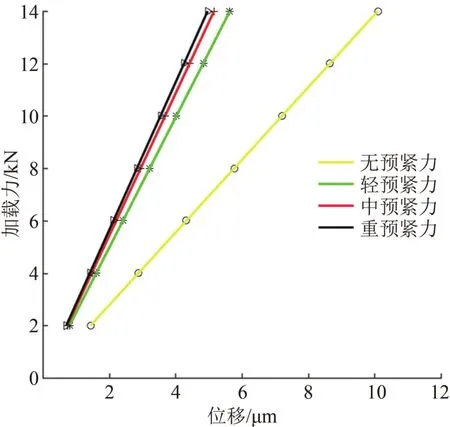
圖5 預緊力對導軌副垂直剛度的影響圖

2.2 預緊力對動剛度的影響

取0.01C、0.05C、0.1C等3種不同的預緊力，根據表1的相關參數，計算出對應的模擬彈簧剛度分別為170.04、177.66、180.51 kN/mm。將建立的三維模型轉換成x＿t格式，導入到Workbench中進行仿真分析，得到不同預緊力下每階模態的振動頻率，結果見表3，不同振型模態結果如圖6所示。可以看出，隨著預緊力的增加，各級固有頻率也隨之增大，說明導軌副的固有頻率受預緊力的影響。

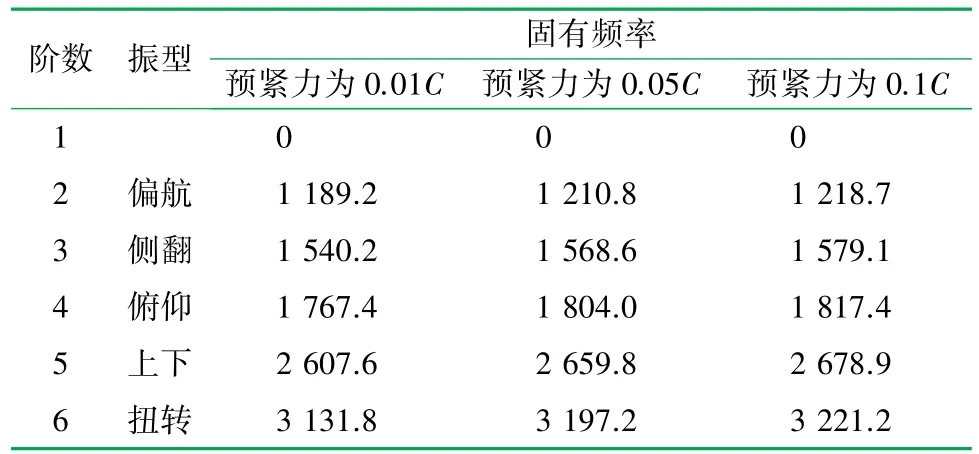
表3 不同預緊力下導軌副的固有頻率表/Hz

為了更加直觀的看出預緊力對導軌副固有頻率的影響，繪制了折線圖，如圖7所示。當預緊力增大時，各階固有頻率也相應增大，這是因為直線導軌副的固有頻率與剛度呈正相關，當導軌副預緊力增大時，其剛度也對應提高，進而各階固有頻率也相應增長，說明直線導軌副的固有頻率與預緊力之間也呈正相關。施加較小的預緊力時，固有頻率增長明顯，當持續增大預緊力時，直線導軌副固有頻率變化明顯變小，所以適當增加預緊力可以提高導軌副動態特性。同時，預緊力過大也提高了接觸面的摩擦力。因此合理選擇預緊力大小直接影響直線導軌副的動態性能。

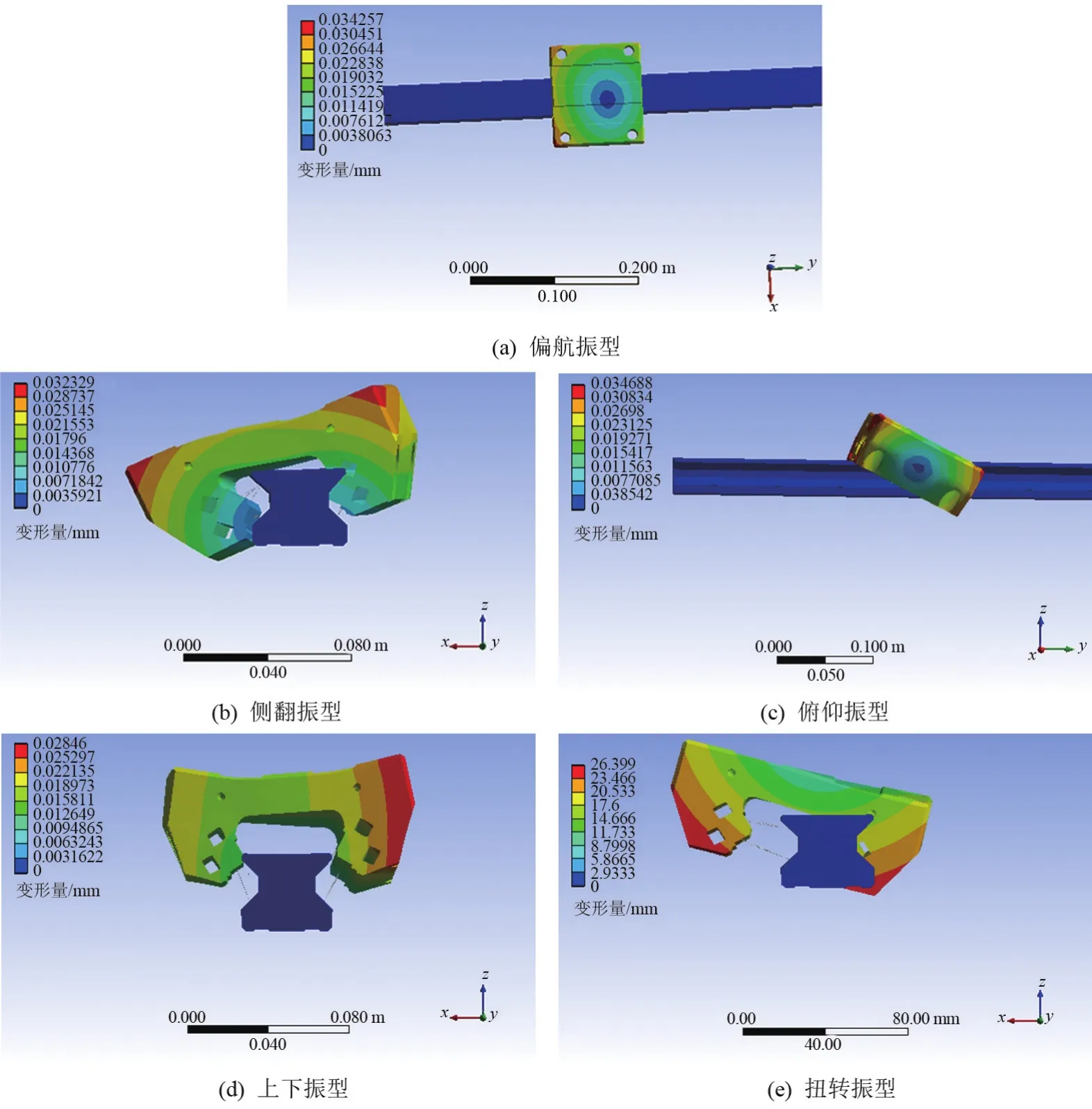
圖6 滾柱直線導軌副的振型圖

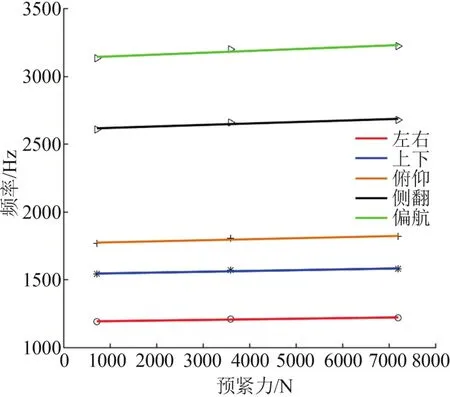
圖7 預緊力對導軌副各階固有頻率的影響圖

3 仿真與試驗結果對比分析

3.1 加/卸載時靜剛度結果

在進行靜剛度試驗時，為了消除滾柱直線導軌副與導軌夾具和滑塊夾具之間的間隙，需要對滾柱直線導軌副施加預加載荷，然后以位移傳感器調零時的數據為起點采集數據。隨著加載力的不斷增加，位移傳感器實時采集滾柱直線導軌副的變形量，稱重傳感器實時記錄加載力的變化量，然后進行垂直載荷的卸載，等到卸載完成后，得到相應的載荷增量和導軌副變形量的數據。加載、卸載時導軌副靜剛度曲線如圖8所示。

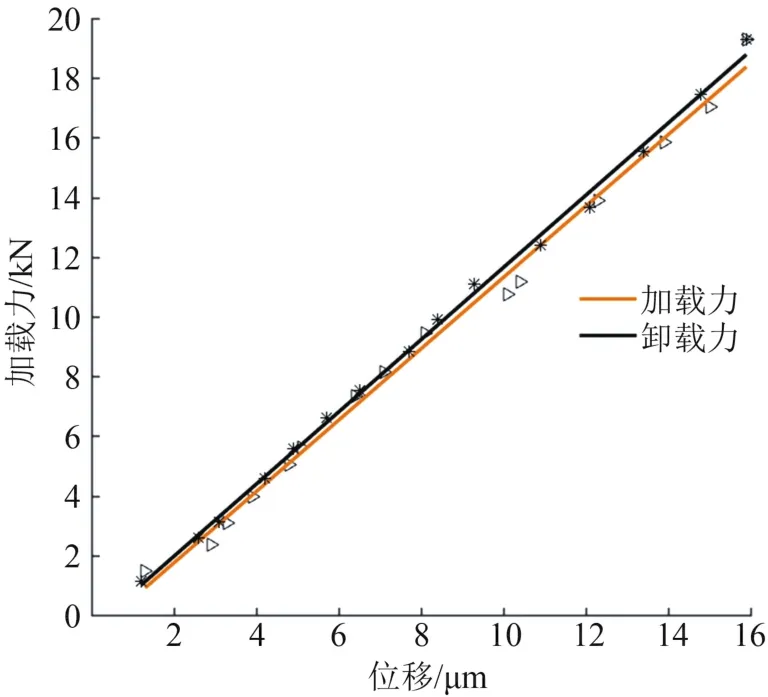
圖8 加/卸載時靜剛度曲線圖

采用最小二乘法對載荷增量和相對變形量進行擬合，得到被測樣件加載靜剛度和卸載靜剛度。可以看出，加載靜剛度曲線和卸載靜剛度曲線不完全重合，但非常接近，在允許的試驗操作誤差范圍內，表明滾柱直線導軌副的性能滿足試驗要求。

將加/卸載狀態下得到的剛度測量均值進行平均得到試驗剛度，試驗靜剛度數據與Workbench仿真的數據進行比較，結果見表4。每次加載或者卸載時靜剛度值浮動較小，其范圍在5 N/μm內，加載與卸載相比靜剛度值偏差較大，范圍在15 N/μm內。與仿真相比，試驗綜合剛度誤差為13.1%，考慮到試驗臺的測量精度，導軌副及夾具的安裝精度，測量誤差在允許的范圍內。因此，靜剛度試驗臺測量的數據是可靠的。

表4 滾柱直線導軌副靜剛度試驗數據表

3.2 不同預緊力導軌副靜剛度對比分析

試驗以JSA-LZG45型滾柱直線導軌副為研究對象，分別選擇無預緊、輕預緊、中預緊、重預緊4種不同等級的預緊力導軌副進行靜剛度試驗測量，將其與仿真數據進行對比。預緊力的等級通過更換滾柱的型號來調節，滑塊、導軌等采用同一樣件。為了提高數據準確性，其他變量全部統一。

根據位移傳感器在各數據采集點的測量值，計算得到相對于預加載時的載荷及變形量。采用最小二乘法對載荷增量和相對變形量數據進行擬合處理，通過數據擬合得到不同預緊力時導軌副靜剛度的對比曲線圖，如圖9所示。當施加輕預緊力時，導軌副的剛度變化明顯，靜剛度增長量為835.58 N/μm，繼續增大預緊力時，導軌副的剛度變化顯著減小；中預緊時靜剛度增長量為91.49 N/μm；重預緊時靜剛度增長量僅為34.20 N/μm。試驗表明:施加較小的預緊力就可以獲得較大的導軌副靜剛度，隨著預緊等級的增大，靜剛度的增長量逐漸變小。

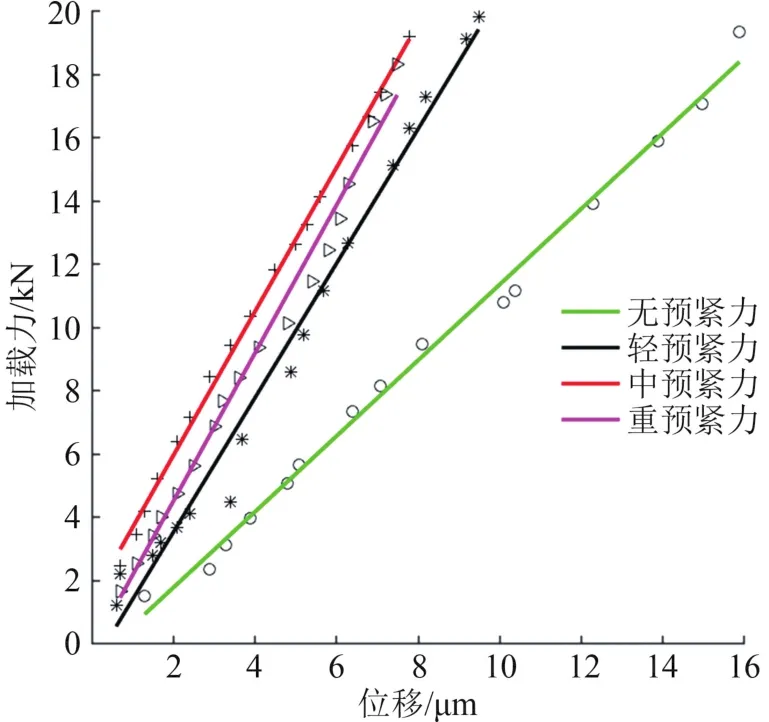
圖9 導軌副靜剛度試驗對比曲線圖

將滾珠直線導軌副靜剛度仿真數據和試驗數據進行對比，結果如圖10所示。靜剛度仿真值和試驗值均隨著預緊力的增大而增大，但是導軌副靜剛度試驗值均低于靜剛度仿真值，輕預緊時，二者相差441.82 N/μm；中預緊時，二者相差 581.23 N/μm。隨著預緊等級的增加，相同預緊等級時仿真與試驗之間的偏差量逐漸變大。

圖10 滾柱直線導軌副靜剛度仿真與試驗對比圖

3.3 滾柱直線導軌副模態試驗研究

模態試驗主要是對導軌副進行結構動力學分析，獲得其固有頻率、振型、模態阻尼和模態剛度等模態參數。通過加速度傳感器和力錘傳感器獲得導軌副的振動信號，振動信號經過數據采集儀和模態分析軟件對結構的試驗數據進行處理和分析，獲得導軌副固有頻率、振型等關鍵參數。

滾柱直線導軌副的高階模態頻率都很高，力錘不能將高階模態激發出來，也超出了所使用的傳感器的識別范圍。所得到的振型與仿真結果基本一致，基本確定試驗操作的準確性。試驗所采用的加速度傳感器是單軸加速度傳感器，只能拾取單維度的振動位移，且在進行激勵時只敲擊了滑塊上表面的測點，忽略了滑塊側面的測點。所以在ADSP V10軟件中，用模態分析模塊進行數據分析，只提取了滾珠直線導軌副滑塊的低階模態。

試驗采用輕預緊、中預緊和重預緊3種預緊等級的導軌副進行模態試驗，在相同試驗條件下進行測試，結果見表5。可以看出，不同預緊力等級下導軌副試驗模態值和仿真模態值基本吻合。隨著導軌副預緊力增大，其固有頻率也隨之增大。

表5 不同預緊力等級導軌副固有頻率數據表/Hz

4 結論

文章建立了滾柱直線導軌副的阻尼彈簧單元的剛度模型，基于ANSYS workbench有限元仿真分析了預緊力對滾柱直線導軌副剛度特性的影響規律，并結合試驗對仿真結果進行了對比分析。主要結論如下:

(1)施加較小的預緊力就可以獲得較大的導軌副靜剛度，但隨著預緊等級的增大，靜剛度的增長量逐漸變小。對滾柱直線導軌副合理施加預緊力，可以顯著提高導軌副的靜剛度，提高滾柱直線導軌副的承載能力。

(2)當滾柱直線導軌副的預緊力增大時，各階固有頻率也相應增大，持續增大預緊力時，滾柱直線導軌副的固有頻率變化明顯變小。合理選擇預緊力大小有助于提高滾動直線導軌副的動態性能。