大型汽輪發電機非全相運行磁密分析

戈寶軍 姜超 陶大軍 趙洪森 陳修材 魯文麗

摘 要：針對非全相運行工況，以一臺1 407 MVA核電汽輪發電機為例，建立了單機無窮大系統動態分析的場-路-網耦合時步有限元模型，分析計算了發電機額定并網運行時變壓器高壓側一相斷開和兩相斷開的非全相運行工況下，汽輪發電機定轉子齒部磁密分布情況及其規律，并將其與正常負載運行時汽輪發電機定轉子齒部磁密分布情況及其規律作對比。最后，提取氣隙磁場密度并分析其變化規律，結果表明非全相運行后，并且除基波最大值下降外其他各次諧波最大值都增大，氣隙磁密畸變較為嚴重。該研究為大型汽輪發電機設計與制造、安裝和維修、運行與操作等工程實踐提供基礎理論參考。

關鍵詞：非全相運行;時步有限元模型;場-路-網耦合;定轉子磁密;氣隙磁場密度

DOI：10.15938/j.jhust.2019.04.001

中圖分類號： TM311

文獻標志碼： A

文章編號： 1007-2683（2019）04-0001-07

Abstract：For the open-phase operation condition operation， taking a 1，407 MW nuclear steam turbine as an example ，a field-circuit-network coupled time-stepping finite element model for a one machine and infinite bus system was set up. The distribution of magnetic field density of the stator and rotor of the turbine generator and its rule were analyzed and calculated under the open-phase operation condition， in which one phase or two phases are open on the HV side of the transformer when the generator is running at the rated operation condition. Then， the magnetic field density distribution of the stator and rotor at the rated load condition for the generator was calculated ，which is compared with the results of the open-phase operation condition. Finally， to extract the air-gap magnetic field density and analyse its change rule， the maximum of the fundamental wave drop and the maximum value of other harmonics are increased ，and the air gap flux density distortion is serious. This study provides the basic theoretical reference for the design and manufacture， installation and maintenance， operation and operation of the large turbine generator.

Keywords：open-phase operation;field-circuit-network coupled;finite element calculation model;magnetic field density of the stator tooth; magnetic field density of the air-gap

0 引 言

大型核電汽輪發電機的非全相運行不僅使定轉子各部分受到極大電磁轉矩沖擊，還對電網造成較大的負面影響。同時，電機齒部磁密畸變不僅導致發電機的渦流和渦流損耗也隨之增大，其必然導致發電機各個部件的溫升相應增大，這樣不但會使發電機的效率降低，同時也使電機運行的安全性和可靠性大大下降[1];而且直接影響電機各部分的受力情況，從而出現局部受力不均，極易發生應力集中的現象[2-3]。同時，通過研究電機內部磁密畸變特點可了解電機各部分鐵耗的分布狀況，為計算定轉子槽漏抗等電機參數提供參考。

對電機磁場密度計算分析一直是工程人員設計時關注的首要基礎問題，學者們進行了大量的研究工作，提出了許多研究方法。文[4]采用有限元方法研究了氣隙磁場并計算了電機的推力，實驗結果很好地驗證了有限元分析的結果。文[5]通過運用有限元方法對凸形槽電機進行模擬仿真，并深入了解轉子齒部磁力線與磁通密度分布場圖，得出凸形槽電機轉子齒磁密分布特點。文[6]采用等效磁路法對氣隙磁密進行了解析， 最后利用有限元法對所設計電機進行了靜態磁場的分析和氣隙磁密計算值的驗證。文[7]利用三維有限元法計算了電機的空載磁場分布，對不同軸向超導勵磁繞組下的磁場以及軸向磁路對徑向磁路的影響進行分析，分析結果通過空載反電動勢實驗得到了驗證。

從眾多學者的研究成果來看，對發電機磁密分布進行了大量研究。但在研究過程中，多是針對單機負載運行情況下，發電機各部分磁密分布情況的研究，而沒有將電網考慮進去，發電機不是在并網條件下運行。同時對發電機非全相工況下，定轉子齒部及氣隙磁密畸變研究較少涉及。

本文建立了單機無窮大系統動態分析的場-路-網耦合時步有限元模型，分析計算了發電機額定并網運行時變壓器高壓側一相斷開和兩相斷開的非全相運行工況下，汽輪發電機定轉子齒部及氣隙磁密畸變情況及其規律;并將其與單機負載運行時汽輪發電機定子齒部磁密分布情況及其規律作對比，得到一些有價值的結論。該研究為大型汽輪發電機設計與制造、安裝和維修、運行與操作等工程實踐提供基礎理論參考。

1 場-路-網模型

1.1 汽輪發電機有限元模型的建立

本文以一臺容量為1 407 MVA汽輪發電機為研究對象，為了簡化計算過程，縮短計算時間，做以下合理假設：由于電機中時變電磁場的變化頻率波動很小，忽略位移電流的影響，將其看成似穩電磁場;假設只考慮即定轉子電流軸向（z向分量） ，將電機有效長度內的磁場視為二維平行平面場;由于電機內磁場的周期性及電機實際結構的對稱性，取其一對磁極的一半作為求解區域;假設忽略定轉子繞組中的集膚效應及電網中的高次諧波作用對電機內磁場的影響;假定鐵心材料具有單值磁化曲線;定子鐵心外邊界散磁均忽略不計。

根據以上的假設條件，建立的汽輪發電機二維有限元計算模型。當利用有限元法分析發電機內電磁場分布時，加上相應的邊界條件，非線性二維平面場用磁矢量AZ位描述時，瞬變電磁場定解問題可以表達為：

1.2 場-路-網耦合模型的建立

本文研究的對象為大型發電機單機無窮大系統，系統的等值電路如圖1所示，其中包括汽輪發電機、勵磁調節系統、轉速控制系統、升壓變壓器、雙回輸電線路以及無窮大系統。

為了分析發電機在并網運行情況下發生非全相運行，建立了1407MVA汽輪發電機場-路-網耦合模型。為了更真實的反映發電機并網運行系統，該模型包括汽輪發電機的有限元模型、勵磁和轉速控制系統、升壓變壓器以及無窮大電網通過150km的雙回架空輸電線進行連接。本文所指的非全相運行是指升壓變壓器高壓側斷路器一相斷和兩相斷開情況下，發電機的不對稱運行狀態。

非全相運行后，電機出現與轉子旋轉方向相反的負向磁動勢，而電機正常運行時僅有與轉子旋轉方向相同的正向磁動勢。該負向磁動勢使電機磁場發生畸變，進而影響電機各部分電磁力的分布。因此，對電機各部分進行磁密分析時，應先分析電機非全相故障穩定后是否在發電機瞬態負序能力范圍內運行，分析如下。

首先，獲得發電機并網額定運行時發生兩種非全相故障情況下定子三相故障電流。然后，通過對稱分量法在獲得的故障電流中提取不同周期內三相不對稱電流的負序分量。其中，故障電流是通過有限元法計算得到的，這里考慮了電機磁場飽和等非線性因素的影響，在此基礎上，通過對稱分量法提取出其中的負序電流分量。最后，根據發電機瞬態負序能力要求，如下式所示，確定電機能夠承受的瞬態負序運行時間t。

∫t0i22dt=（I2）2t=A（2）

式中：I2為瞬態負序電流的標幺值;常數A與發電機結構和通風冷卻方式有關，該電機A=5s。本文研究發現，發電機并網額定運行時發生兩種非全相故障穩定運行后，電機仍然在瞬態負序運能力內運行，故本文僅分析此時電機故障后再次達到運行平穩后電機各部分磁密分布情況及其規律。

2 非全相運行時磁密分析

2.1 非全相運行定子電流分析

若汽輪發電機啟動后達到平穩運行時，發生變壓器高壓側單相或兩相突然斷路故障，即電機非全相運行。斷路后電機穩定運行時定子電流4個周期內變化情況如圖2所示。

由圖2（a）可知，A相斷后電機穩定運行定子電流有很大的沖擊，其中B相最為嚴重，最大幅值為57281.29A，為B相額定電流最大幅值的1.10倍，A、C相定子電流減小，其中A相最大幅值為37590.09A，其額定電流最大幅值的0.71倍，C相最大幅值為39421.42A，其額定電流最大幅值的0.75倍。由圖2（b）可知，B、C相斷后電機穩定運行定子電流較A相斷后電機后定子電流沖擊更為嚴重，其中A、C相最為嚴重，最大幅值分別為為71194.04A、71218.85A，分別為A、C相額定電流最大幅值的1.33倍、1.35倍，B相電流最大幅值為0.165476A，與額定值相比幾乎視為零。電機聯網額定負載運行時定子電流如圖2（c）所示。

2.2 非全相運行定子齒部磁場畸變分析

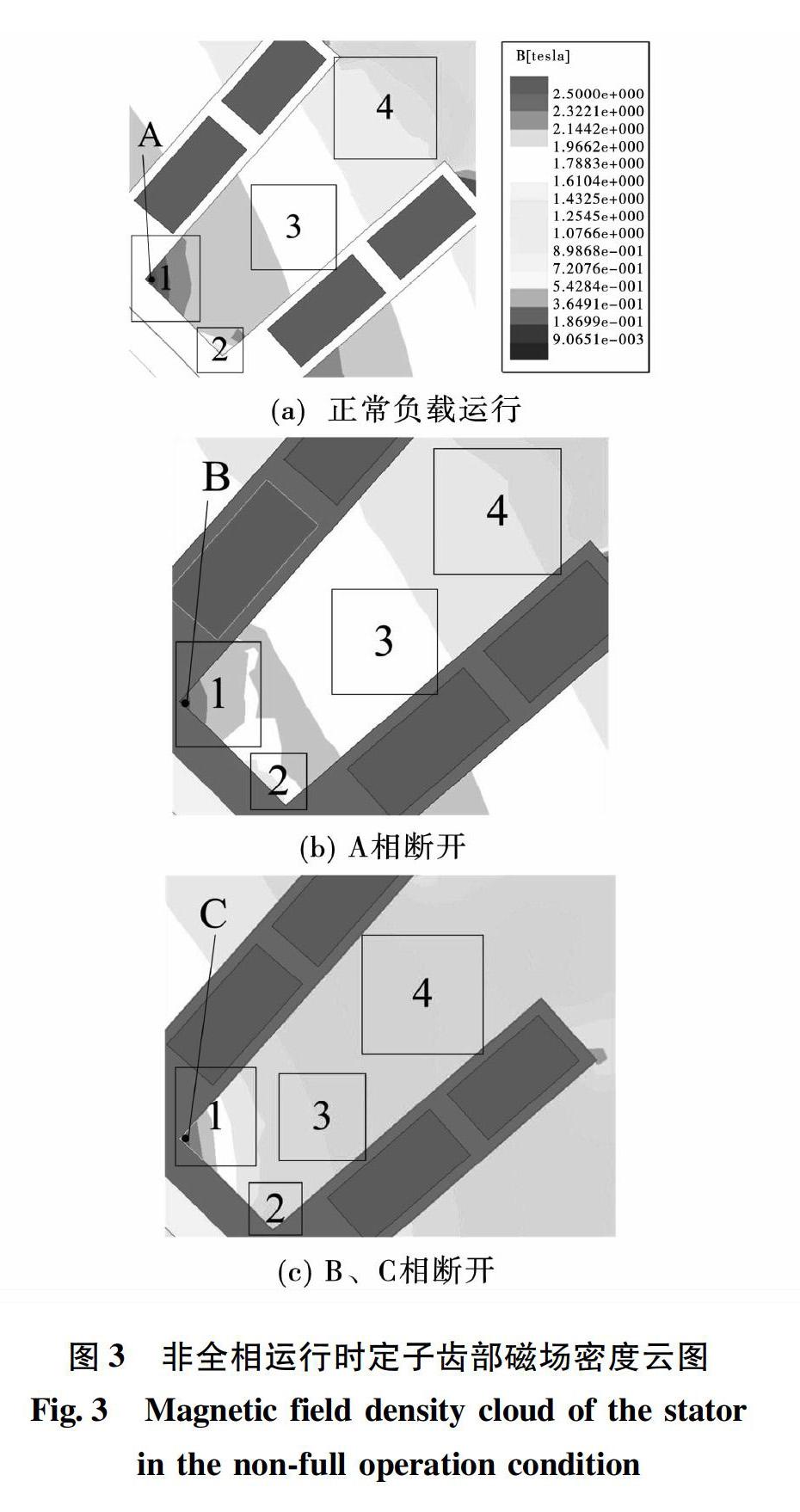
電機聯網正常負載運行穩定運行時定子齒部磁密云圖如圖3（a）所示。為了方便分析，將該定子齒齒壁沿轉子旋轉方向分別稱作后壁、前壁。汽輪發電機啟動后達到平穩運行時，發生負載單相或兩相突然斷路故障，即電機非全相運行后電機再次達到平穩運行時的定子同一齒部磁密發生畸變。此時， A相斷開電機穩定運行時齒部磁密云圖，B、C相斷開后電機穩定運行齒部磁密云圖如圖3（b）、（c）所示。

由圖3（a）知，電機聯網正常負載運行穩定運行時齒部磁場，其中磁場強度由定子齒底至齒頂沿徑向方向逐漸變大，其中有部分區域則分布更為復雜，如2區的磁場密度先變大后變小，再變大。由1區、3區、4區可知，定子齒部此時沿轉子旋轉方向的靠近前壁的區域磁場密度較大，而2區稍有不同。此時磁密最大點A點，其值為2.453T。

由圖3（b）知變壓器高壓側A相斷開后穩定運行時齒部磁場發生嚴重畸變，其中磁場強度由定子齒底至齒頂沿徑向方向逐漸變大，其中有部分區域則畸變更為復雜，如1區、2區的磁場密度先變大后變小，再變大。由3區、4區可知，定子齒部此時沿轉子旋轉方向的靠近前壁的區域磁場密度較大，而2區稍有不同。此時磁密最大點B點，其值為2.124T，為電機聯網正常負載運行時相應點相應時刻最大值的0.866倍。

由圖3（c）知，變壓器高壓側B、C相斷開后穩定運行時齒部磁場發生嚴重畸變，其中磁場強度由定子齒底至齒頂沿徑向方向逐漸變大，其中有部分區域則畸變更為復雜，如2區的磁場密度先變大后變小，再變大。由1區、3區、4區可知，定子齒部此時沿轉子旋轉方向的靠近前壁的區域磁場密度較大，而2區稍有不同。此時磁密最大點C點，其值為2.012T，為電機聯網正常負載運行時相應點相應時刻最大值的0.820倍。

由上分析可知，非全相運行后電機穩定運行時，定子齒部磁場密度電機聯網正常負載運行時減小，其中A相斷路故障后穩定運行時定子齒部3區、4區磁場密度減小最為明顯，B、C相斷開后穩定運行時齒部2區、3區、4區磁場密度減小最為明顯。而就定子齒部整體而言，在發電機旋轉方向的后側磁密較弱，而在旋轉方向的前方一側磁密則較強，其中B、C相斷開時更為明顯。

2.3 非全相運行轉子磁場畸變分析

電機聯網正常負載運行穩定運行時轉子齒部磁密云圖如圖4（a）所示。為了方便分析，將該轉子齒齒壁沿轉子旋轉方向分別稱作后壁、前壁。汽輪發電機啟動后達到平穩運行時，發生負載單相或兩相突然斷路故障，即電機非全相運行后電機再次達到平穩運行時的轉子同一齒部磁密發生畸變A相斷開后穩定運行時齒部磁密云圖，B、C相斷開后穩定運行齒部磁密云圖如圖4（b）、（c）所示。

由圖4（a）知，電機聯網正常負載運行穩定運行時轉子磁場分布情況。其中小齒部分磁場密度由小齒齒底至齒頂沿徑向方向逐漸變小，每一個小齒磁密后壁部分與前壁部分相比較大;而大齒部分磁場密度由轉子軸心向轉子表面沿徑向先變大后變小，再變大，有部分更為復雜。

由圖4（b）知，A相斷開后穩定運行時齒部磁場發生嚴重畸變，其中磁場強度小齒部分磁場密度由小齒齒底至齒頂沿徑向方向逐漸變小，每一個小齒磁密后壁部分與前壁部分相比較大。在大齒部分由1區、4區可知，轉子齒部此時沿轉子旋轉方向的靠近前壁的區域磁場密度較大，而整體磁密較正常負載運行減小，2區最為明顯。

由圖4（c）知，BC相斷開后穩定運行時齒部磁場發生嚴重畸變，其中磁場強度小齒部分磁場密度由小齒齒底至齒頂沿徑向方向逐漸變小，每一個小齒磁密后壁部分與前壁部分相比較大，磁密較正常負載運行減小。在大齒部分由1區、4區可知，轉子齒部此時沿轉子旋轉方向的靠近前壁的區域磁場密度較大，而整體磁密較正常負載運行減小，2區最為明顯。

由上分析可知，非全相運行后電機穩定運行時，轉子磁場密度電機聯網正常負載運行時減小，其中A相斷路故障后穩定運行時定子齒部1區、2區、3區磁場密度減小最為明顯，B、C相斷開后穩定運行時齒部1區、2區、4區磁場密度減小最為明顯。而就轉子齒部整體而言，在發電機旋轉方向的后側磁密較強，而在旋轉方向的前方一側磁密則較弱，其中B、C相斷開時更為明顯。

2.4 非全相運行氣隙磁密畸變分析

根據二維場-路-網耦合有限元磁場計算結果，首先對汽輪發電機啟動后達到平穩運行后，發生變壓器高壓側單相或兩相突然斷路故障，即電機非全相運行后電機再次達到平穩運行時一個周期內典型時刻氣隙磁密波進行分析，其中一個周期內典型時刻氣隙磁密波的變化情況分別如圖5（a）、（b）所示。

由表1、結合圖5可以看出，A相斷開后電機穩定運行一個周期內氣隙磁密最大幅值為1.661T，為最小幅值的1.02倍，B、C相斷開后電機穩定運行一個周期內氣隙磁密最大幅值為1.674T，為最小幅值的1.05倍。因此，非全相運行電機穩定后氣隙磁密波較正常運行時波動較為嚴重，研究其主要形成原因如圖6所示。

由圖6（a）知，非全相運行后，電機出現與轉子旋轉方向相反的負向磁動勢F-，而電機正常運行時僅有與轉子旋轉方向相同的正向磁動勢F+。若負向磁動勢F-與正向磁動勢F+旋轉至如圖6（b）所示位置，此時電機磁動勢取得最小值，磁密波亦取得最小值。若負向磁動勢F-與正向磁動勢F+旋轉至如圖6（c）所示位置，此時電機磁動勢取得最大值，磁密波亦取得最大值。因此，非全相運行后氣隙磁密隨時間而波動。在上述分析基礎之上，對一個周期內典型時刻氣隙磁密進行諧波分析，得到典型時刻典型次諧波幅值變化情況如圖7所示。

由圖7（a）可以看出，A相斷路發電機再次達到穩定運行時1個周期內，1階齒諧波23次和25次諧波變化明顯，較正常運行時增大，其最大幅值分別為0.0826T、0.0599T，為額定值的1.706倍、1.371倍。而基波密幅值下降，其它各次諧波最大幅值均增大。其中基波磁密，最大幅值為1.550T，較額定時降低;3次，5次諧波及9次諧波磁密幅值最大為0.825T，0.105T，0.269，較額定運行時增大。

由圖7（b）可以看出，BC相斷路發電機再次達到穩定運行時1個周期內，1階齒諧波23次和25次諧波化明顯，較正常運行時增大，其最大幅值分別為0.0872T、0.107T，為額定值的1.801倍、2.456倍。而基波磁密幅值下降，其它各次諧波最大幅值均增大。其中基波磁密，最大幅值為1.550T，較額定時降低;3次，5次諧波及9次諧波磁密幅值最大為0.825，0.467T，0.269，較額定運行時增大。

對電機非全相運行后電機達到平穩運行時，一個周期內典型次諧波最大值、最小值如表2、表3、表4所示。

由表2、表3、表4可知，就電機氣隙磁密而言，A相斷路發電機再次達到穩定運行時1個周期內，基波最大值為1.550T，最小值為1.193T，分別為額定運行時的0.955倍、0.735倍。其他各次諧波最大值都增大，其中3次、5次、23次最為嚴重，其一個周期內最大值為0.825T，0.391T，0.0826T，分別為正常運行時的2.266倍、4.374倍、1.707倍。

BC相斷路發電機再次達到穩定運行時1個周期內，基波最大值為1.548T，最小值為1.089T，分別為額定運行時的0.954倍、0.671倍。其他各次諧波最大值都增大，其中3次、5次、9次最為嚴重，其一個周期內最大值為0.820T、0.467T、0.269T，分別為正常運行時的2.253倍、5.224 倍、1.830 倍。

非全相發生后發電機再次達到穩定運行時一個周期內，與正常運行時相比，除基波最大下降外，其他各次諧波最大值都增大，并且 B、C相斷路基波較A相斷路時氣隙基波減小更多，其他各次諧波最大值增大更為嚴重。

3 結 論

本文建立了單機無窮大系統動態分析的場-路-網耦合時步有限元模型，分析計算了發電機額定并網運行時變壓器高壓側一相斷開和兩相斷開的非全相運行工況下，汽輪發電機定子齒部磁密分布情況及其規律，主要結論為：

1）非全相運行后電機穩定運行時，定轉子磁場密度電機聯網正常負載運行時減小且磁場畸變較為嚴重;發電機定子旋轉方向的后側磁密較弱，而在旋轉方向的前方一側磁密則較強，而就轉子整體而言，在發電機旋轉方向的后側磁場很強，而在旋轉方向的前方一側磁場則較弱，其中B、C相斷開時更為明顯。

2）非全相運行后電機穩定運行時，除基波最大下降外，其他各次諧波最大值都增大，并且BC相斷路基波較A相斷路時氣隙基波減小更多，其他各次諧波最大值增大更嚴重。

參 考 文 獻：

[1] 殷繼偉，戈寶軍，陶大軍，等.大型半速汽輪發電機非全相工況下轉子渦流損耗的研究[J]. 中國電機工程學報，2016（20）：5647.

[2] 梁艷萍，于鴻浩，邊旭. 汽輪發電機三相突然短路故障轉子動態電磁力計算[J]. 電工技術學報，2016（11）：91.

[3] 陳陽生，林友仰. 永磁電機氣隙磁密的分析計 算[J]. 中國電機工程學報，1994（5）：17.

[4] 盧琴芬，葉云岳. 混合勵磁直線同步電機的磁場與推力[J]. 中國電機工程學報，2005（10）：127.

[5] 陳學鋒，孫躍，王漢豐，鮑曉華. 凸形槽電機轉子齒磁密分析[J]. 電機與控制應用，2014（8）：28.

[6] 何海波，劉海龍. 異步電機徑向電磁力的分析[J]. 微電機，2011（8）：26.

[7] 曹江華，楊向宇，肖如晶. 雙轉子徑向永磁電機氣隙磁密的分析計算[J]. 微電機，2010（8）：28.

[8] 車良松，潘柏松，戈道川，鄭立君，劉偉江. 輪轂式永磁無刷直流電機空載氣隙磁密波形的模擬分析[J]. 機電工程，2011（3）：374.

[9] 江紅軍. 發電機非全相運行的危害與預防策略[J]. 電力科學與工程，2008（6）：55.

[10]彭翔，賈志東，王黎明，關志成，程星鑫，王天正. 大型發電機定子槽楔松動研究及檢測[J]. 中國電機工程學報，2007（30）：9.

[11]齊利曉. 盤式無鐵心永磁電機氣隙磁場與永磁體渦流損耗分析[D].天津：天津大學，2007.

[12]趙朝會，李遂亮，王新威，等. 永磁同步電機氣隙磁密影響因素的分析[J]. 河南農業大學學報，2005（3）：338.

[13]陳陽生，林友仰. 永磁電機氣隙磁密的分析計算[J]. 中國電機工程學報，1994（5）：17.

[14]高旭東，王希鳳，曹珊珊，等.開關磁阻電機磁密及鐵耗分析[J].黑龍江工程學院學報，2017，31（4）：27.

[15]吳奕菡. 壓縮機負載下永磁同步電機損耗分析及優化設計[D].沈陽：沈陽工業大學，2017.

[16]鄭軍銘. 球磨機直驅用超低速大轉矩永磁同步電動機研究[D].沈陽：沈陽工業大學，2017.

[17]蔣山. 轉子偏心狀態下永磁同步電機電磁性能分析[D].哈爾濱：哈爾濱理工大學，2017.

[18]仲昊. 氣隙偏心與匝間短路復合故障下的繞組受力分析[D].北京：華北電力大學，2017.

[19]鐘鴻敏，左曙光，吳旭東，等.電勵磁爪極發電機氣隙磁場與徑向電磁力的解析計算模型[J].電工技術學報，2017（7）：49.

[20]曹海翔，沈靖文，王善銘，等.永磁直流電機定子的振動分析[J].清華大學學報（自然科學版），2017（1）：89.

（編輯：溫澤宇）