基于布爾網絡的語義悖論研究

陳智斌

（1.華南師范大學政治與行政學院，廣州510631；2.廣東技術師范大學計算機科學學院，廣州510665）

0 引言

語義悖論（Semantic Paradox）是一種與計算機科學，特別是數理邏輯理論研究密切相關的邏輯悖論，這一點早已通過哥德爾不完全性定理及其對角線引理所揭示[1]。說謊者悖論是最為古老而典型的語義悖論，它可以用自然語言表達如下：

語句(L)為假 (L)

語義不穩定是語義悖論語句表現最為突出的現象。就以說謊者悖論為例，當對語句(L)賦值為真（假）時，它在下一階段將為假（真），而在再下一階段又變為真（假），如此反復。也就是說，說謊者語句(L)有悖于常理之處在于，無論如何賦值都無法斷定(L)的真假。為此，需要回答以下問題：是什么導致了悖論語句的語義不穩定？

上述問題可借助計算工具加以討論。已有一些學者嘗試通過計算工具研究語義悖論的語義不穩定性[2]。然而，上述工作僅研究了說謊者悖論及其變體的語義不穩定現象，并沒有一般性地探討語義悖論的語義不穩定現象。為此，本文把研究范疇擴展到布爾悖論上。布爾悖論是語義悖論的一種子類型，說謊者悖論即屬于布爾悖論。以下是一個關于布爾悖論的典型例子[3]：

從以上例子可見，布爾悖論的特點是其中每條語句均等價于一組語句的布爾組合，而每條語句的真值又取決于其他語句的真值。受此啟發，本文發現布爾網絡（Boolean Network）作為一種廣泛應用在生物學、復雜系統研究中的數學模型[4]，與布爾悖論存在等價關系。因此，本文將通過引入布爾網絡及其相關分析理論和計算工具，利用布爾悖論與布爾網絡的等價性，在系統層面分析并研究布爾悖論的語義不穩定性，探究形成語義不穩定性背后的系統性因素。

1 布爾系統與布爾網絡

1.1 布爾系統

這里主要研究帶有真謂詞的語義悖論（即真理論悖論），真謂詞是指用于斷定語句真假的謂詞。例如前面舉例提到的說謊者悖論，語句(L)斷定了自身為假，因此其形式語言表達中應含有真謂詞以及否定符號。在悖論研究中，布爾系統是指根據對角線引理構造的一組語句集。為給出布爾系統的定義，首先引入帶真謂詞的算術語言及相關概念。記N 是包含0 的自然數集，設L 為算術語言，N 是L 的標準結構，Th( )N 是L中的真算術理論。在L 中加入真謂詞T 得到L+，設X是關于T 的解釋，以N+X?A 表示A 在模型N+X 中為真并簡記為X?A。L+的真算術理論Th+( )N 包含了所有滿足如下條件的語句A：對任意X，有。為簡化表示，使用X( A)=1 代替，使用X( A)=0代替N+X?A。給出有關定義如下：

定義1（布爾系統）[6]有窮語句集Δ={δi|1 ≤i ≤n}稱為是一個布爾系統，如果對每個1 ≤i ≤n，都存在布爾組合式fi，使得：

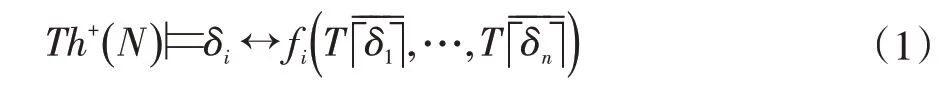
在上述定義中，fi(p1,…,pn)是通常的命題公式，p1,…,pn是其中可能出現的命題變元。是在fi(p1,…,pn)中對p1,…,pn分別同時代入得到的語句。其中是語句δi的哥德爾編碼表示該編碼在L 中對應的數字，并且把形如的語句簡記為。后面把fi稱為一個布爾組合，同時它也代表對應的布爾函數（真值函數）。

定義3（修正周期）[6]設Δ 是語句集，X0?N。數m ≥1 稱為是Δ 在X0上的修正周期（簡稱周期），如果存 在N ≥0，使 得 對 任 意k ≥N 和 任 意 A ∈Δ，Xk+m(A)=Xk(A)都成立。稱m 是Δ 的一個周期，如果m是Δ 在某個X0上的周期。稱除自身外不能被Δ 的其他周期整除的周期為Δ 的主周期。

給 定 布 爾 系 統Δ={δi|1 ≤i ≤n}和X0?N，稱Xk(δ1)Xk(δ2)…Xk(δn)(k ≥0)為Δ 的一個真值排列。給定修 正 序 列，稱 對Δ 的 真 值 排 列 按k=0,1,…排序而構成的序列為Δ 的一個修正序列。在文獻[6]中已經證明，對任意X0?N，布爾系統在階段k+1 的真值排列由階段k 的真值排列決定，且按如下規則計算：

1.2 布爾網絡與布爾系統的等價性

布爾網絡是由N 個變量v1,…,vN構成的有向圖，圖中每個節點對應一個變量。每個變量均只有0 或1兩種可能取值并由布爾函數fi:{0,1}ki→{0,1}決定，其中ki表示節點vi共有ki條輸入邊。布爾網絡中各節點的輸入邊數目（入度）可以相同，也可以不同。往往規定各節點入度均為K，如果允許各節點入度不同，則取平均入度作為參數K[4]。布爾網絡也稱為N-K 模型。需要指出的是，為一般地研究布爾網絡的特性，更常見的布爾網絡模型是隨機布爾網絡，即給定節點數目及網絡平均入度的取值范圍，隨機地選取網絡樣本，但在每個網絡演化過程中網絡拓撲和布爾組合不變。因此許多布爾網絡的研究結論是在統計意義上成立。在一些文獻中會更確切地使用“隨機布爾網絡”（Random Boolean Network）這樣的術語。

布爾網絡屬于一種離散動力系統（Discrete Dynamical System），即按離散的時間點更新網絡中各節點的狀態。稱排列v1(t)v2(t)…vN(t)是布爾網絡在時刻t(t=0,1,…)的狀態s(t)，其中vi(t)是vi在時刻t 的取值。稱序列s(t )s( t+1) s( t+2 )…是布爾網絡的一段演化軌跡（Trajectory）。布爾網絡的演化規則如下，在每個離散時刻t+1，變量vi的取值vi(t+1)由在時刻t 的ki個輸入決定：

比較式（2）和式（3）容易發現，布爾系統修正序列的真值排列計算規則與布爾網絡的演化規則本質是相同的。對于具有n 條語句的布爾系統和具有N 個節點的 布 爾 網 絡(n=N)，設X0(δ1)X0(δ2)…X0(δn)=v1(0)v2(0)…vN(0)，取相同的布爾組合fi（1 ≤i ≤n），對所有k=t，布爾系統在階段k 的真值排列等同于布爾網絡在時刻t 的狀態。

定義4（等價性）稱布爾系統Δ 和布爾網絡Ω 是等價的，如果Δ 與Ω 使用同一組布爾組合 fi（1 ≤i ≤n）。

合肥市軌道交通1號線車站建筑方案設計的思路及探討………………………………………………………… 閆陽（10-44）

1.3 布爾網絡吸引子與語義穩定性

一旦布爾系統被表示為等價的布爾網絡后，布爾網絡動力學理論及工具就能為研究布爾系統的語義行為提供一條全新的途徑。利用布爾網絡的計算機模擬工具，能夠獲得任意布爾系統的語句真值變化過程。而且，根據布爾系統和布爾網絡的等價性，兩者的許多性質可以互相印證和使用。例如，記布爾網絡所有可能狀態構成的集合為S，則（N 是節點個數）。由于S 是有窮的且演化按式（3）進行因而是確定性的（Deterministic），因此布爾網絡從任意初始狀態出發演化都必然會有狀態重復出現，使得網絡的演化軌跡呈現周期性。布爾網絡的周期性通過吸引子（Attractor）來表達，它是S 的一個非空子集，一旦網絡演化到某個吸引子中的某一狀態后，演化軌跡將按確定次序反復遍歷吸引子內各狀態。顯然，一個布爾網絡的吸引子長度（即吸引子中的網絡狀態數目）相當于布爾系統的一個周期。由以上討論可知布爾網絡至少有一個吸引子，換言之布爾系統至少有一個周期。而且由于S 是有窮的，顯然布爾網絡只存在有窮多個吸引子，對應地布爾系統只存在有窮個主周期。這一點同樣已經在布爾系統的相關研究中被證明了[6]。

本文基于布爾網絡的吸引子對布爾系統的語義穩定性定義如下。

定義5（語義穩定性）設布爾系統Δ 有等價的布爾網絡Ω，Ω 的吸引子集合為A。對于a ∈A即為吸引子長度。劃分Δ 的語義穩定性如下：

（2）稱Δ 是語義不穩定的，如果存在a ∈A，|a |＞1。特別地，稱Δ 是悖論的，如果對所有a ∈A，|a |＞1。

2 實驗方法及結果

2.1 實驗方法

本節將通過實驗討論在引言中提出的問題：是什么導致了悖論語句的語義不穩定？針對當前所要研究的對象，該問題可具體化為：為什么有的布爾系統是語義穩定的，但有的卻是語義不穩定的？兩類布爾系統之間在什么方面存在差異？

首先，利用歸一化漢明距離（Hamming Distance）函數能夠計算布爾系統的兩條真值排列的差異程度，而真值排列的差異程度即反映了悖論語句集的語義不穩定性。根據按前面所給的布爾網絡定義，歸一化漢明距離函數可表示如下：

根據上述漢明距離函數定義布爾系統的語義不穩定度。然后利用布爾系統與布爾網絡的等價關系，可對用于分析布爾網絡動力學特性的德里達曲線（Derrida curves）[7]方法加以改造。具體定義如下：

定義6（語義不穩定度）設布爾系統Δ 有等價的布爾網絡Ω，Ω 的吸引子集合為A。對每個a ∈A，設a={s1,…,sm}且s1s2…sm是Ω 的一段演化軌跡。稱是a 的周長，其中H 是歸一化漢明距離函數。Δ 的語義不穩定度為Ω 所有吸引子的周長之和。

定義7（德里達曲線）設布爾系統Δ 有等價的布爾網絡Ω。在時刻t 任取Ω 的一個狀態s(t)，有ρ(t)=H(s(t),s(t+1))和ρ( t+1)=H( s( t +1),s( t+2 ))，其 中H 是歸一化漢明距離函數。稱(ρ(t),ρ( t+1))為Δ 的德里達曲線上的一個點。

定義7 實際是把布爾系統的一段包含有3 個階段的修正序列轉換為德里達曲線中的一個點。在這段修正序列中，ρ(t)表示了布爾系統從時刻t 到t+1 有多少語句的真值發生變化，ρ( )t+1 則表示了這些變化在再下一階段給系統造成多大的后續變化。因此，布爾系統的德里達曲線反映了其語句真值變化的傳遞特性。本文稱布爾系統中語句真值變化的傳遞特性為它的系統穩定性。下面通過實驗分析系統穩定性對布爾系統的語義不穩定性的影響。

2.2 實驗結果

本實驗通過在MATLAB 軟件上編寫程序（使用了http://www.teuscher.ch/rbntoolbox/提供的工具箱），隨機構造布爾系統作為統計樣本并將它們按語義穩定性分類。實驗中分別從節點個數N=10,12 的布爾網絡中各隨機選取了1000 個樣本，它們的平均入度K 取值范圍均為1～5。假設已得到若干個具有相同語義穩定性的布爾系統，根據定義7 可隨機地抽取這組布爾系統的德里達曲線上的點并將抽取結果合并，由此得到具有某種語義穩定性的布爾系統的德里達曲線，統計結果如圖1 所示。

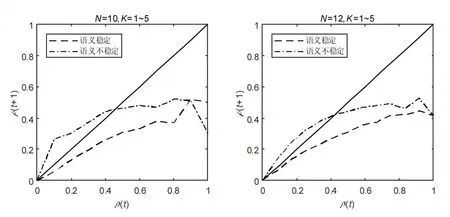
圖1 語義穩定和不穩定的布爾系統的德里達曲線

從圖1 可見到，在統計意義上語義不穩定的布爾系統的德里達曲線基本位于語義穩定的布爾系統對應曲線的上方，這表明任意時刻在語句真值變化程度相同的情況下，與語義穩定的布爾系統相比，語義不穩定的布爾系統會在下一時刻引致更多語句的真值發生變化。也就是說，對于語義不穩定的布爾系統，它的系統穩定性較低，而對于語義穩定的布爾系統，它的系統穩定性較高。而且，語義不穩定的布爾系統有一部分曲線位于圖中對角線（即直線ρ(t+1)=ρ(t)）的上方且與對角線相交于原點外的另一點。因此從統計意義上來看，此類系統在演化過程中ρ(t)將收斂于該交點，使得系統中語句真值持續地變化下去，從而形成了語義不穩定的現象。與此相反，對于語義穩定的布爾系統，曲線在圖中對角線的下方并只與對角線交于原點，因此語句真值變化所帶來的影響會被逐漸消減為零。

表1 從實驗樣本集抽取了五個典型例子，由表中結果可見，系統穩定性越低的布爾系統，其語義不穩定度越大。這一結論與圖1 的統計結果相一致，表明系統穩定性，即布爾系統中語句真值變化的傳遞特性對于語義穩定性所起的作用。

表1 一些布爾系統實例

3 結語

為探究語義悖論的語義不穩定現象，本文利用布爾網絡的計算工具及分析理論通過計算實驗探討了布爾悖論語義不穩定的系統性因素。實驗結果表明，對于系統穩定性較低的布爾系統，語句真值的變化通過語句間網絡關系一直傳遞下去，從而形成了語義不穩定現象。進一步，可利用本文所介紹的工具和方法研究語義悖論的自指性。