串列六邊形截面橋塔氣動干擾效應研究

張志杰,李永樂,向活躍,房 忱

(西南交通大學土木工程學院,成都 610031)

在土木工程領域,越來越多地出現多個建筑或者建筑構件彼此相鄰的情況,如相鄰的兩幅橋梁[1],懸索橋的兩根大纜[2],城市中的互相靠近的高層建筑等。由于相互之間的氣動干擾,這些建筑或者建筑構件的氣動力和它們單獨存在時有著明顯的差異。所以,研究串列的建筑或者建筑構件的氣動相互干擾非常必要。

早在20世紀70年代,Zdravkovich[3-4]就對圓柱的氣動干擾問題有了一定的研究。日本學者Kimura[5]通過風洞實驗，研究了新建橋梁對已有橋梁的氣動干擾效應,結果表明雙幅橋梁在不同間距和不同風向角下的氣動干擾效應十分顯著。Irwin等[6]通過風洞實驗的節段模型和全橋模型，研究了在塔科馬老橋附近新建一座橋梁時兩幅橋梁的氣動穩定性。Jin[7]等通過試驗研究了串列雙幅斜拉橋的渦激共振的氣動干擾效應；劉志文等[8-10]對串列雙幅斷面的渦激共振穩定性、顫振穩定性、三分力系數氣動干擾效應，進行了相關的風洞試驗或數值模擬。林震云[11]從氣動剛度和氣動阻尼的角度，分析了雙幅橋梁的氣動干擾效應對下游橋梁的顫振穩定性的影響。劉多特等[12]采用一種改進的數值模擬方法,研究了主梁斷面高度、來流風攻角及風向等因素對錯列雙鈍體斷面間的氣動特性影響。李勝利等[13-14]通過CFD數值模擬,研究了串列鈍體的三分力氣動干擾效應和門形橋塔馳振氣動干擾效應。陳星宇[15]以數值模擬的方法研究了懸索橋門形橋塔雙柱串列的氣動性能。路毓[16]對大跨橋梁的橋塔的吊索鈍體群的氣動干擾進行了數值分析。唐浩俊[17]以橋塔的兩串列帶圓角方柱為研究對象,研究了風速、風向角和間距比對截面氣動力系數的影響。李燕玲等[18]與試驗結果對比驗證了DES方法在高雷諾數并列雙圓柱繞流的準確性。已有研究大多通過風洞試驗或數值模擬直接得到氣動干擾效應的結果,分析過程較少而且分析的截面大都比較常規,多為矩形或者箱形。綜合上述文獻,針對特殊截面形式的串列建筑或者建筑構件的氣動干擾問題有必要進行深入的研究。

本文根據一座人字形串列六邊形截面橋塔的斜拉橋,分別取塔柱的上游、下游單個截面和不同間距的串列雙柱進行CFD數值模擬,得到各種情況下的三分力系數,并結合壓力云圖進行氣動干擾效應的分析,為橋梁抖振和馳振的研究提供依據。本研究的橋塔截面為沿橋梁橫橋向不對稱的六邊形截面,氣動力特性較為特殊,相關研究較少,研究其氣動力特性非常具有工程意義。

1 分析模型

1.1 工程概況

某大橋的主塔為人字形橋塔,主塔正面如圖1所示。橋塔截面在橫橋向為不對稱的六邊形截面,為研究串列雙柱的氣動干擾效應,分別取上游、下游單個橋塔截面以及選取如圖1所示3個高度位置處的塔柱進行數值模擬研究,3個高度位置處的串列塔柱從高到低分別為截面1、截面2和截面3。高度不同,串列塔柱截面的間距就不同,高度越低,間距越大。

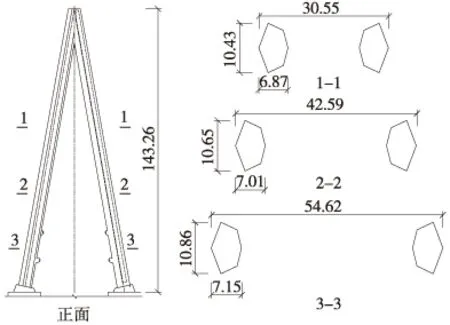
圖1 橋塔正面及橋塔截面(單位：m)

由于塔柱截面是漸變的、相似的,單個截面情況選取3種高度位置中頂部的截面進行研究。計算風攻角在-10°～10°,每2°為一個工況的三分力系數。圖2給出了計算風攻角和風向。

圖2 攻角和風向示意

1.2 計算域以及網格劃分

利用Flunent 14.0計算流體力學軟件,對單個橋塔塔柱截面進行數值模擬時,參考有關文獻[19],為保證阻塞率小于3%的要求,上側和下側邊界距離截面形心200 m,而上游邊界距離截面左側邊界150 m,下游邊界距離截面右側邊界450 m,模型縮尺比為1∶100。網格的劃分兼顧計算精度和計算效率,在靠近截面區域采用非結構化網格,適當加密網格；在遠離截面區域,適當讓網格稀疏,采用結構化網格。計算域網格劃分如圖3所示,劃分網格數量為20萬個。計算域的邊界條件設置為：上游側設為速度入口,入口速度為15 m/s,下游側設為壓力出口,上下側為對稱邊界條件,橋塔的六邊形截面設為無滑移壁面。本文計算時所采用的湍流模型為SSTk-ω模型,時間步長取為t=0.001 s,待計算穩定后便可以計算三分力系數。對串列橋塔塔柱截面進行數值模擬時,計算域大小和模型縮尺比以及網格劃分方法同單個截面,計算域網格劃分如圖4所示。邊界條件和湍流模型與單個截面的相同,時間步長同樣取為t=0.001 s,分別監視上游、下游截面的三分力時程結果,待計算穩定后計算三分力系數。

圖3 單個截面計算域網格劃分

圖4 串列橋塔截面計算域網格劃分

2 數據處理及模型驗證

在計算穩定后,根據數值模擬得到的三分力系數按照式(1)～式(3)計算截面的三分力系數平均值。

(1)

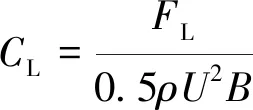
(2)

(3)

式中,ρ為空氣密度；U為來流風速；D為垂直于來流方向的截面高度；B為平行于來流方向的截面寬度。

為了驗證數值模擬的正確性,采用14 m×14 m的正方形截面,縮尺比為1∶100,網格劃分、邊界條件及Fluent中的設置同單個橋塔截面。圖5為正方形截面的三分力系數數值模擬結果和文獻[20]的對比圖。從圖5可以看出,正方形截面在攻角為0°時的阻力系數最大,正攻角時隨攻角的增大而減小,負攻角時隨攻角的增大而增大,正攻角和負攻角的模擬值呈對稱關系；而升力系數隨著攻角的增大而減小,斜率為負值。從模擬結果來看,阻力系數和升力系數與文獻的試驗值吻合程度較好,雖然部分攻角下略有偏差,可能是由于縮尺比不同,文獻試驗存在的誤差等因素的影響,可以認為本文所采用的數值模擬方法是正確且合理的。

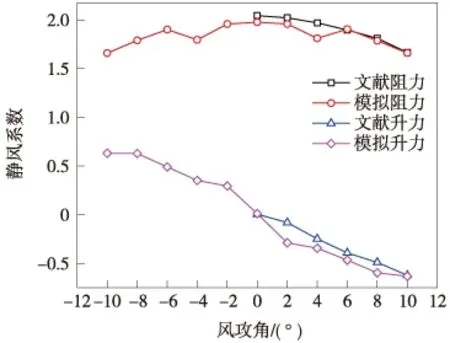
圖5 正方形截面靜風系數模擬值與文獻試驗值對比

3 塔柱氣動特性分析

3.1 單個塔柱的氣動特性

上游、下游橋塔截面的三分力系數模擬結果如圖6所示。

圖6 單個橋塔截面三分力系數

比較兩個截面的模擬結果,可以看出上游、下游橋塔截面的阻力系數在0°攻角時最大,正攻角時隨攻角的增大而減小,負攻角時隨攻角的增大而增大,正攻角和負攻角的模擬值呈對稱關系；上游截面比下游截面的阻力系數大,從圖7的壓力云圖來看,這可能是由于下游截面在來流風作用下更呈流線型,對來流的阻擋作用更小；上游截面的升力系數隨風攻角的增大而減小,下游截面的升力系數隨風攻角的增大而增大,可能是由于上下游兩個截面在橫橋向是不對稱的且差異較大,所以上下游兩個截面的變化趨勢完全相反；而上下游兩個截面的力矩系數隨攻角的變化趨勢一致,且下游截面的力矩系數較大。

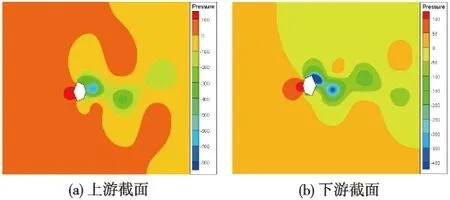
圖7 單個截面0°攻角的壓力云圖

3.2 串列橋塔的相互氣動干擾

在計算結果穩定后,提取出三分力監視結果,按照第2節公式計算得到三分力系數平均值。為了能夠直觀地分析串列截面的氣動干擾效應,將單個截面的三分力系數和串列截面的三分力系數繪于一張圖上。圖8是不同間距串列塔柱的上游截面與單個上游截面的三分力系數圖。圖8(a)表明,截面1串列兩截面距離很近,從圖9的壓力云圖可以看出,上游截面的阻力,相互之間的氣動干擾效應導致上游截面的阻力系數與單個截面相比有所增加,而且在0°風攻角附近,這種阻力系數的增加效應最大；截面2和截面3兩截面之間的距離增大,由于塔柱間干擾效應會減弱,截面2和截面3的上游截面的阻力系數會比單個截面的有所減小。圖8(b)的結果說明在0°風攻角時，各截面的升力系數與單個截面的相同,但是當攻角較大時,各工況在氣動干擾效應下有不同程度的差異。從圖8(c)中,可以清楚地看出截面1在攻角較大時,串列塔柱的氣動干擾效應會使得力矩系數與單個截面的差異較大,且隨著兩截面間距離的增大,這種差異會減小。

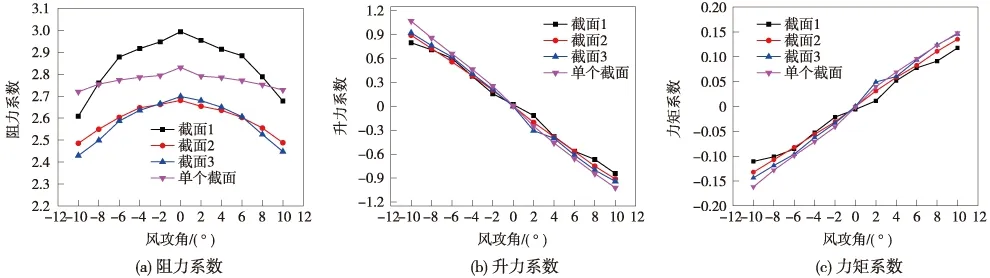
圖8 不同間距上游橋塔截面與單個上游截面三分力系數

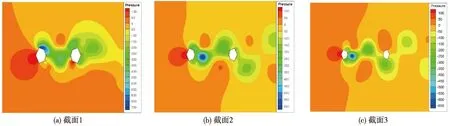
圖9 0°攻角下不同間距串列塔柱的壓力云圖

圖10為不同間距串列塔柱的下游截面與單個下游截面的三分力系數圖。圖10(a)表明,各截面的下游截面的阻力系數都比單個截面的小,從圖9的壓力云圖可以看出,這是由于上游截面的遮擋效應造成下游截面的阻力明顯降低；而截面1兩截面的距離最近,氣動干擾效應和上游截面的遮擋效應最大,下游截面出現負壓,阻力系數最小為負值；截面2和截面3兩截面的距離比截面1的距離大,遮擋效應和氣動干擾效應減弱,下游截面壓力增大,阻力系數增大。從圖10(b)可以看出,由于上游截面的遮擋效應,各截面的下游截面升力系數的斜率比單個截面的要小。圖10(c)的結果表明,3種截面下游截面的力矩系數基本相同,與單個下游截面相比,隨著攻角的變化,整體變化趨勢相同,但力矩系數增加較小。

圖10 不同間距下游橋塔截面與單個下游截面三分力系數

4 結論

通過數值模擬,分析了串列橋塔的相互氣動干擾,考察了風攻角、塔柱間距等因素的影響,得出如下結論。

(1)對單個塔柱截面來說,上游截面比下游截面的阻力系數大,隨攻角變化的規律相同；上下游截面的升力系數的變化趨勢相反；上下游兩個截面的力矩系數基本相同。

(2)對串列塔柱的上游截面來說,距離較小時,阻力系數比單個截面的要大,距離較大時,阻力系數比單個截面的要小；塔柱間距離變化時,升力系數和力矩系數的差異較小。

(3)對串列塔柱的下游截面來說,下游截面的阻力系數都比單個截面的小,塔柱間的距離增大時,阻力系數有所增大；而升力系數和力矩系數的斜率都比單個截面的要小。