基于博弈論和迪杰斯特拉算法的大型建筑逃生方案研究

陳虹呂 鄧怡然

摘要：隨著社會發展，公共安全受到人們的廣泛關注。本文針對具有參觀性質的大型復雜建筑，以盧浮宮為例，全面分析建筑物內的人群分布和流動特點，給出了基于博弈論的人群行為分析和基于迪杰斯特拉算法的MSTS模型以制定人群疏散的路線。最后本文將該模型應用于盧浮宮，計算出游客的逃生時間，驗證了模型的可行性。

關鍵詞：博弈論;羊群效應;快即是慢;光程;迪杰斯特拉算法

中圖分類號：TP18 文獻標識碼：A 文章編號：1007-9416（2019）07-0125-03

0 引言

大型復雜且具有參觀性質的建筑，是人群集中度較高的場所，我們不得不考慮到各種可能發生的安全事故，例如火災、地震、恐怖襲擊等，提前為緊急情況下的人群疏散制定可行路線是非常重要且有現實意義的。本文針對這一問題，在第一部分先介紹了人群在緊急情況下疏散的典型特征，第二部分在此基礎上給出了多人博弈時個體行為對個人利益和集體利益的影響。第三部分通過將“光程”的概念類比于疏散路程，制定了基于迪杰斯特拉算法的逃生路線。在最后驗證了該模型的有效性和可行性。

1 人群疏散行為分析

宏觀上來看，群體的疏散過程就是由個體與周圍環境、與其他個體之間相互作用而形成的整體所呈現出來的運動現象。疏散過程中個體的心理變化對疏散策略的選擇、疏散所需時間有非常重要的影響，所以理解個體的心理和行為對提高人群疏散效率有重要作用。典型的群體疏散行為特征有以下幾種[1]：

1.1 從眾現象

在群體疏散過程中，個體由于群體的壓力或影響改變其原有的行走策略轉為和大多數個體相同的行走策略，即為從眾現象，也稱隨大流行為或羊群行為。一定程度上，這種盲目從眾行為是不理智的。

1.2 瓶頸拱形現象

如果人群具有相同的目標方向，疏散開始時，人群個體的運動方向都是直行通向出口處的，出口處的人員密度逐步增加。隨著這個過程的持續，出口處的人流通行能力達到飽和。此時，個體根據實際情況需要尋找其他的替代方向。個體選擇新方向的過程中，依然希望能到達盡量距離出口最近的位置。在圓形中，圓心到該圓上每一點的距離相等，由于出口處通行能力的限制，當更多期望距離出口最近的個體到達出口處時，聚集在出口的人群將形成類似圓形的排布[2]。

1.3 快即是慢

當出口處人群密度較高時，群體所需的疏散時間將隨著個體速度的加快先縮短再增加。由于個體之間行為不能統一，若部分個體加快速度，則出口處個體間的相互摩擦、干擾增強，導致總體前行的阻力加大，使出口處的人群疏散效率降低，即“快即是慢”效應[3]。因此人群疏散過程中個體不能盲目加速，應該有序前行，以保證穩定的人群疏散效率。

2 基于博弈論的分析

2.1 博弈論理論

博弈論主要是研究存在競爭情況下、主體行為相互影響時，各參與者的決策及決策均衡的理論。游客疏散過程是期望以最短時間到達目標地點的個體面對空間競爭以及周圍個體做出搶行、避讓、繞行的不同選擇時優化自身選擇的過程。疏散空間的限制，造成空間的稀缺性，個體向目標地點靠近的過程實質上是一個具有競爭性質的階段。博弈論可以將決策的過程完整展示出來，這樣能很好地解釋人員個體選擇行走策略的心理作用過程，更貼合實際的疏散過程中心理作用的重要影響。

2.2 問題分析

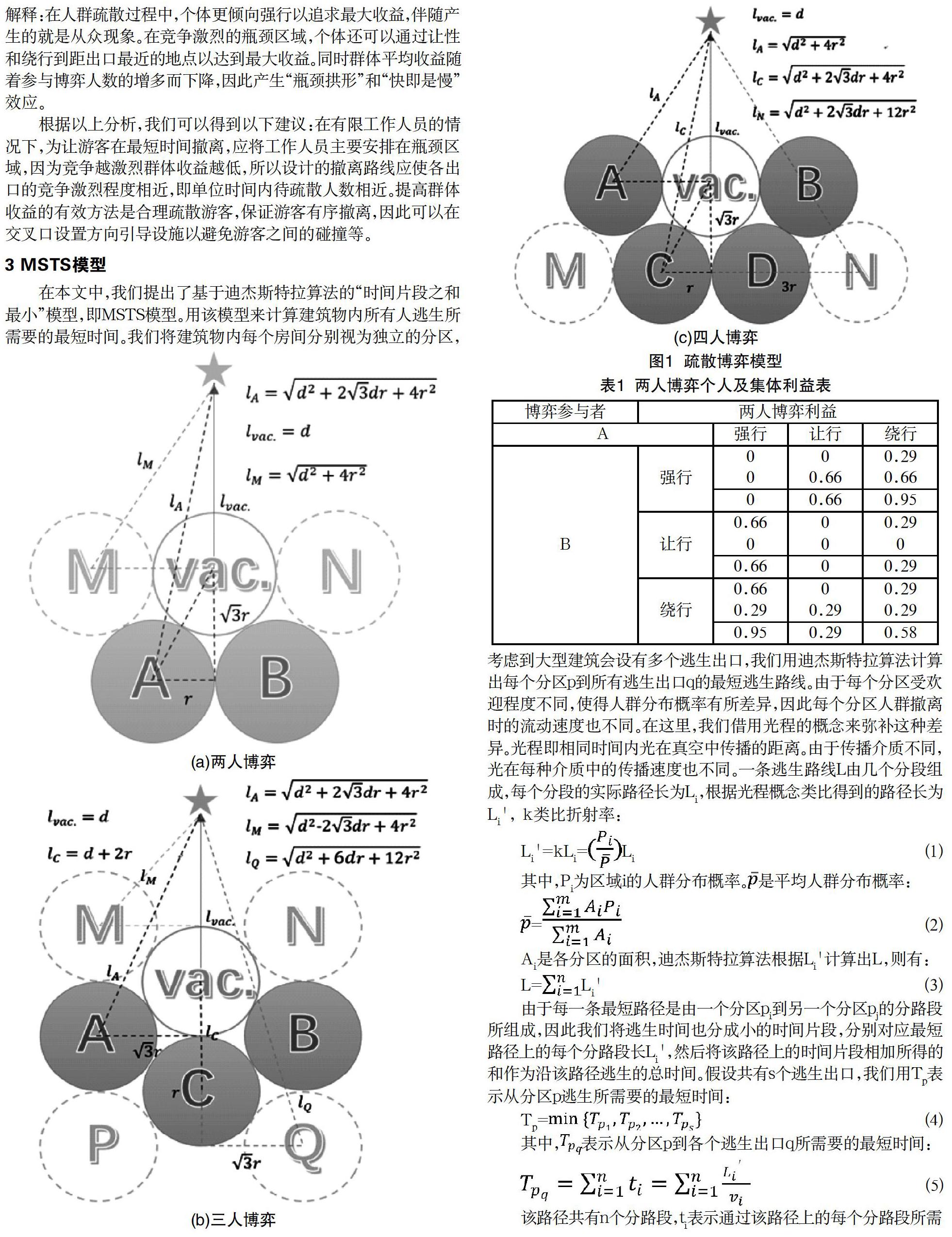
根據人體工程學理論，人體可以被看作是長軸為61cm，短軸為45.6cm的橢圓體[4]。在擁擠的條件下，我們可以把人體在垂直于地面的投影簡化為半徑r為0.45m的圓形。考慮最可能出現的博弈情況有二人博弈、三人博弈、四人博弈，如圖1（a）（b）（c），并做以下假定：

（1）每個圓形只能代表一名參與者，虛線圓圈表示尚未被占據，可由相鄰圓形“繞行”占據，實線圓圈表示各參與者的競爭對象，其圓心到目標地點（星號表示）距離為d;（2）各參與者至多有“搶行”“讓行”“繞行”三種策略，彼此緊密相鄰，表現為各圓形相切;（3）各參與者移動速度相同，且一次博弈只能移動二倍半徑2r或不移動;（4）個體收益用參與者在博弈前后距目標地點的距離差表示，即：個體收益Pi=Li博弈前-Li博弈后。群體收益為個體收益之和。

兩人博弈個人及集體利益如表1所示，三人博弈個人及集體利益如表2所示，四人博弈個人及集體利益如表3所示。

從表1、表2、表3我們可以發現，對于群體來說：兩人博弈時，群體最大收益為一人繞行、一人強行，群體最小收益為兩方均強行或均繞行;三人博弈時，群體最大收益為兩人繞行、一人強行，群體最小收益為兩人強行、一人繞行;四人博弈時，群體最大收益為三人讓行、一人強行或繞行，群體最小收益為兩人繞行，兩人強行或讓行。而對于個體來說：兩人博弈時，最大收益決策為強行;三人博弈時，最大收益決策為強行或繞行;四人博弈時，最大收益決策為強行或讓行。

當個體追求最大利益時，群體收益不可能達到最大。由此可以解釋：在人群疏散過程中，個體更傾向強行以追求最大收益，伴隨產生的就是從眾現象。在競爭激烈的瓶頸區域，個體還可以通過讓性和繞行到距出口最近的地點以達到最大收益。同時群體平均收益隨著參與博弈人數的增多而下降，因此產生“瓶頸拱形”和“快即是慢”效應。

根據以上分析，我們可以得到以下建議：在有限工作人員的情況下，為讓游客在最短時間撤離，應將工作人員主要安排在瓶頸區域，因為競爭越激烈群體收益越低，所以設計的撤離路線應使各出口的競爭激烈程度相近，即單位時間內待疏散人數相近。提高群體收益的有效方法是合理疏散游客，保證游客有序撤離，因此可以在交叉口設置方向引導設施以避免游客之間的碰撞等。

3 MSTS模型

在本文中，我們提出了基于迪杰斯特拉算法的“時間片段之和最小”模型，即MSTS模型。用該模型來計算建筑物內所有人逃生所需要的最短時間。我們將建筑物內每個房間分別視為獨立的分區，考慮到大型建筑會設有多個逃生出口，我們用迪杰斯特拉算法計算出每個分區p到所有逃生出口q的最短逃生路線。由于每個分區受歡迎程度不同，使得人群分布概率有所差異，因此每個分區人群撤離時的流動速度也不同。在這里，我們借用光程的概念來彌補這種差異。光程即相同時間內光在真空中傳播的距離。由于傳播介質不同，光在每種介質中的傳播速度也不同。一條逃生路線L由幾個分段組成，每個分段的實際路徑長為Li，根據光程概念類比得到的路徑長為Li'， k類比折射率：

4 結語

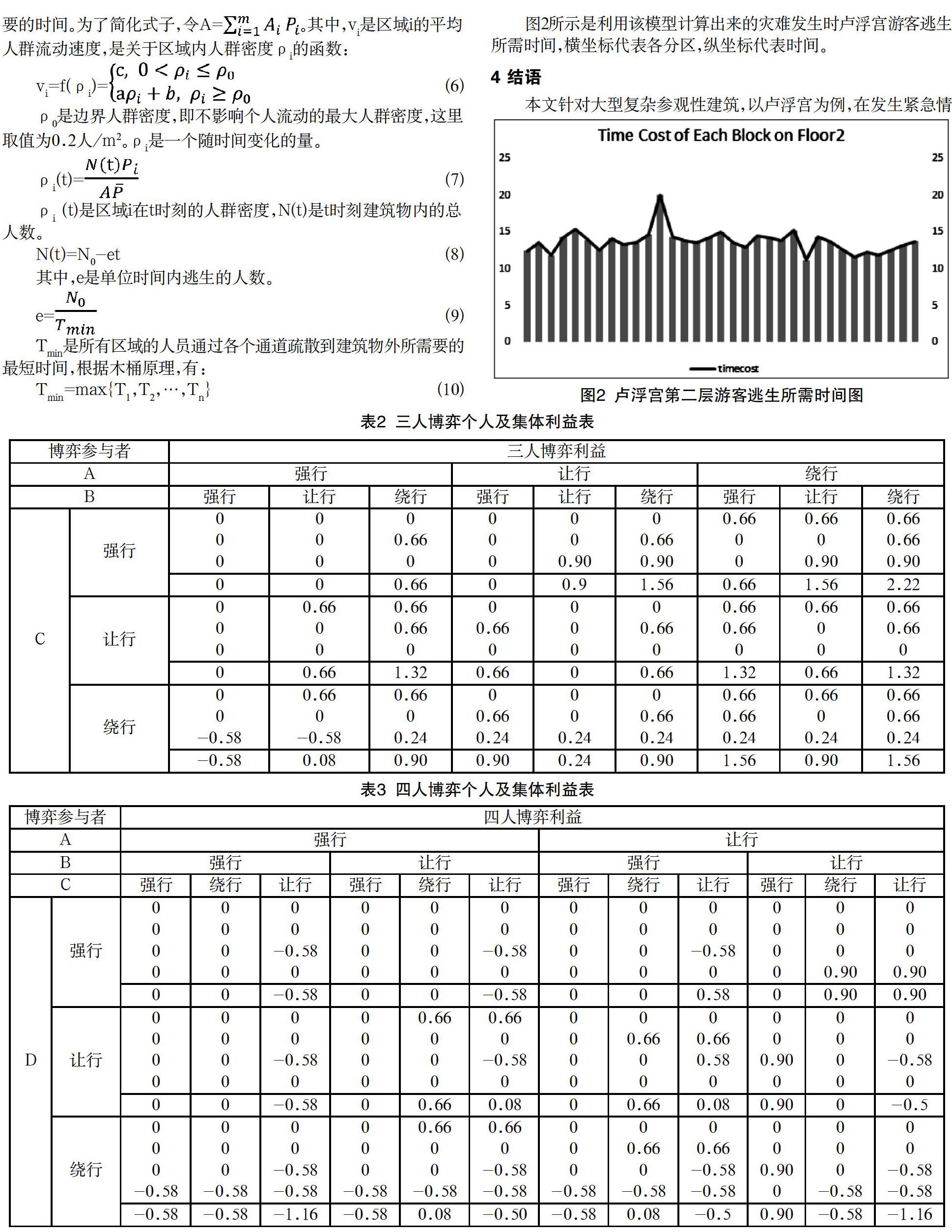
本文針對大型復雜參觀性建筑，以盧浮宮為例，在發生緊急情況時，首先用博弈論方法分析了游客逃生時因心理變化產生的行為，個體利益與群體利益的關系。接著用迪杰斯特拉算法計算出建筑內各區域到各出口的最短逃生路線，這里借用了“光程”的概念，不止是考慮實際疏散路程長短，也根據人群密度對疏散速度的影響，對人群分布概率的不對等做出了彌補。分析結果顯示該模型具有很好的可行性，這在我們為大型復雜建筑設計室內逃生路線時提供了新方法，具有很好的現實意義。

參考文獻

[1] 劉根旺，周穎，張磊，康增信.基于博弈論的人員疏散演化研究[J/OL].計算機工程與應用：1-8[2019-07-23].

[2] Dirk Helbing，Illes Farkas，Tamas Vicsek.Simulating dynamical features of escape panic[J].Nature，2000（03）：487-490.

[3] 李蘋.基于博弈論方法的人員運動規律研究[D].華北水利水電大學，2017.

[4] 付婷.城市軌道交通車站集散能力瓶頸識別[D].北京交通大學，2014.