基于油耗的米勒循環與高壓縮比相關性研究

智鑫，寧智，呂明，李岳

(1.北京交通大學機械與電子控制工程學院,北京 100044；2.北京交通大學動力總成新能源汽車北京市重點實驗室,北京 100044)

隨著混合動力汽車的快速發展，混合動力專用發動機對燃油經濟性的要求越來越高。米勒循環通過調節進氣門的關閉時刻控制進氣量、缸內氣體壓縮終了溫度和壓力，從而降低發動機的有效壓縮比，得到一種膨脹比大于有效壓縮比的熱力學循環模式[1-3]。提高壓縮比可以有效提高發動機的理論熱效率，但與此同時會帶來嚴重的爆震現象，如果通過推遲點火的方式來降低爆震，會導致燃油經濟性嚴重下降[4-5]。

國內外已有一些關于米勒循環與高壓縮比的相關研究[2-6]，但關于兩個技術間的相互作用，尤其是米勒循環與高壓縮比在燃油經濟性以及爆震方面的相關性分析較少，有待進一步研究。鑒于以上背景，本研究利用GT-Power軟件，對一款1.2 L渦輪增壓缸內直噴3缸汽油發動機進行仿真建模，并搭載米勒循環與高壓縮比技術，在此基礎上對米勒循環、高壓縮比在燃油經濟性方面的影響規律以及二者間的相關性進行分析。

1 計算模型建立與驗證

1.1 發動機基本參數

采用1.2 L渦輪增壓缸內直噴3缸汽油機作為原型發動機，其基本參數見表1。利用GT-Power軟件進行仿真建模。

表1 原型發動機基本參數

1.2 待研究工況及發動機建模參數

一般來說，混合動力發動機取消怠速工況，高熱效率區在2 000～4 000 r/min之間的中高負荷工況，因此本研究選擇了3個高熱效率工況點(見圖1)進行分析，分別為工況1(2 500 r/min，1.2 MPa)、工況2(3 000 r/min，1.4 MPa)和工況3(3 500 r/min，1.4 MPa)。原型發動機在3個工況下的配氣正時以及點火時刻數據如表2所示。

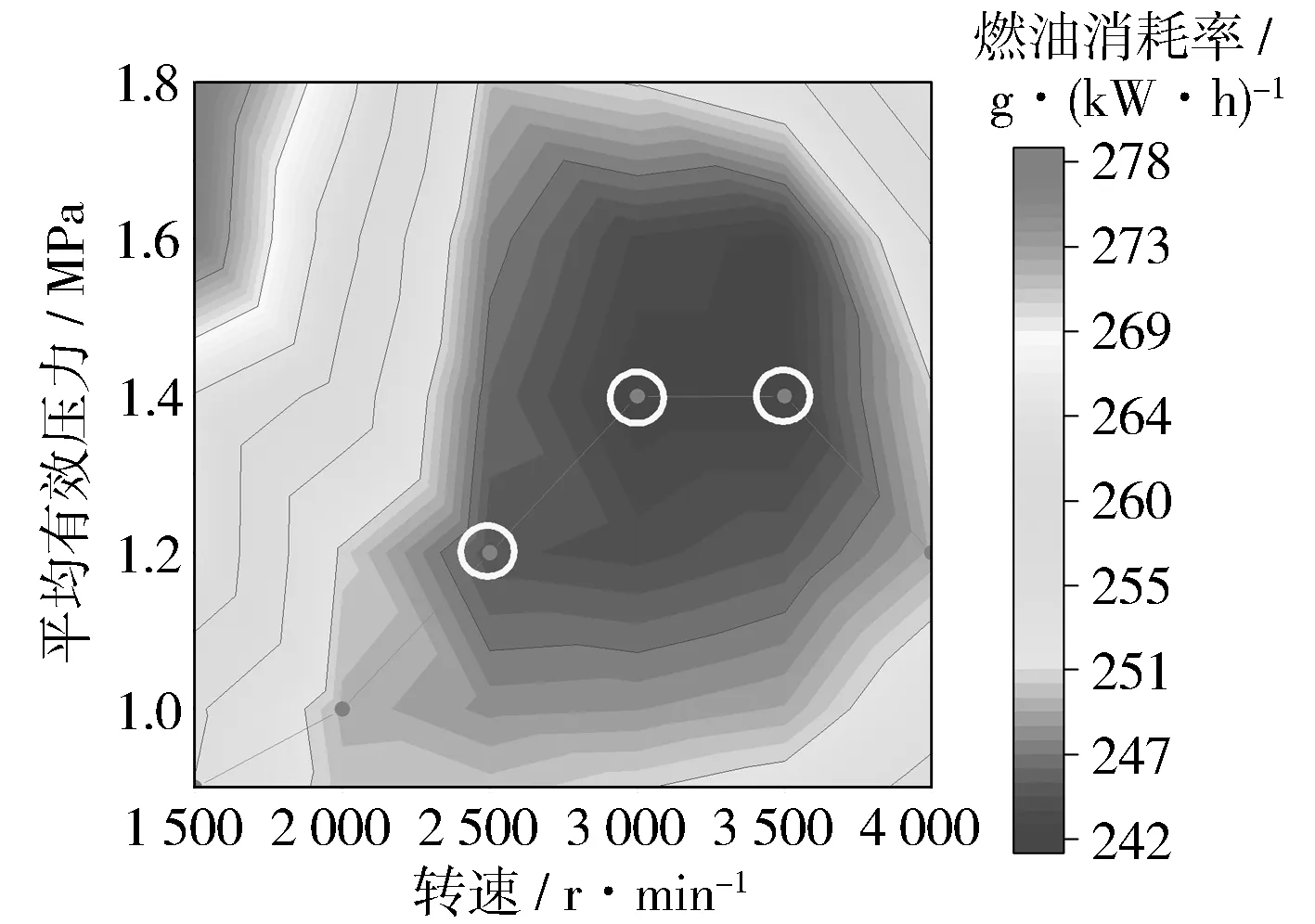
圖1 燃油消耗率特性

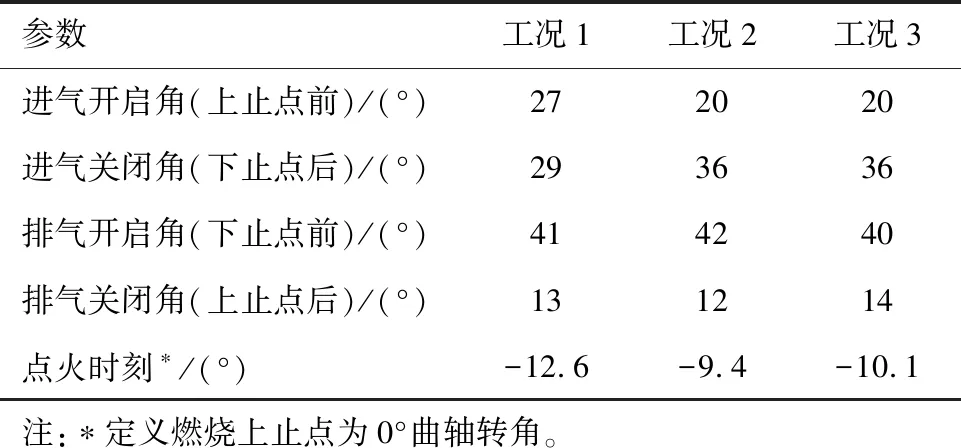
表2 原型發動機運行參數

除此之外，在建模過程中還需要重點考慮缸內燃燒模型與缸內傳熱模型。

缸內燃燒模型選擇了湍流火焰燃燒模型SITurb，與常用的韋伯模型相比，采用湍流火焰燃燒模型可以有效預測非標定工況下的缸內燃燒放熱率。SITurb模型需要考慮缸內燃燒室形狀、點火位置、點火時刻、混合氣運動以及燃料物性等因素的影響[7]。燃燒模型的準確性直接影響缸壓的準確性。

傳熱模型直接影響排氣溫度，對發動機性能的準確預測具有重要影響。通常將整個燃燒室壁分為活塞、氣缸蓋和氣缸套三部分，分別進行燃燒室壁面傳熱量計算。其中，在給定壁面面積和壁面溫度的情況下，利用Woschni半經驗公式求解各部分的傳熱系數[7]。

根據上述工況、運行參數、燃燒模型以及傳熱模型等，建立了發動機GT-Power工作過程仿真模型(見圖2)。

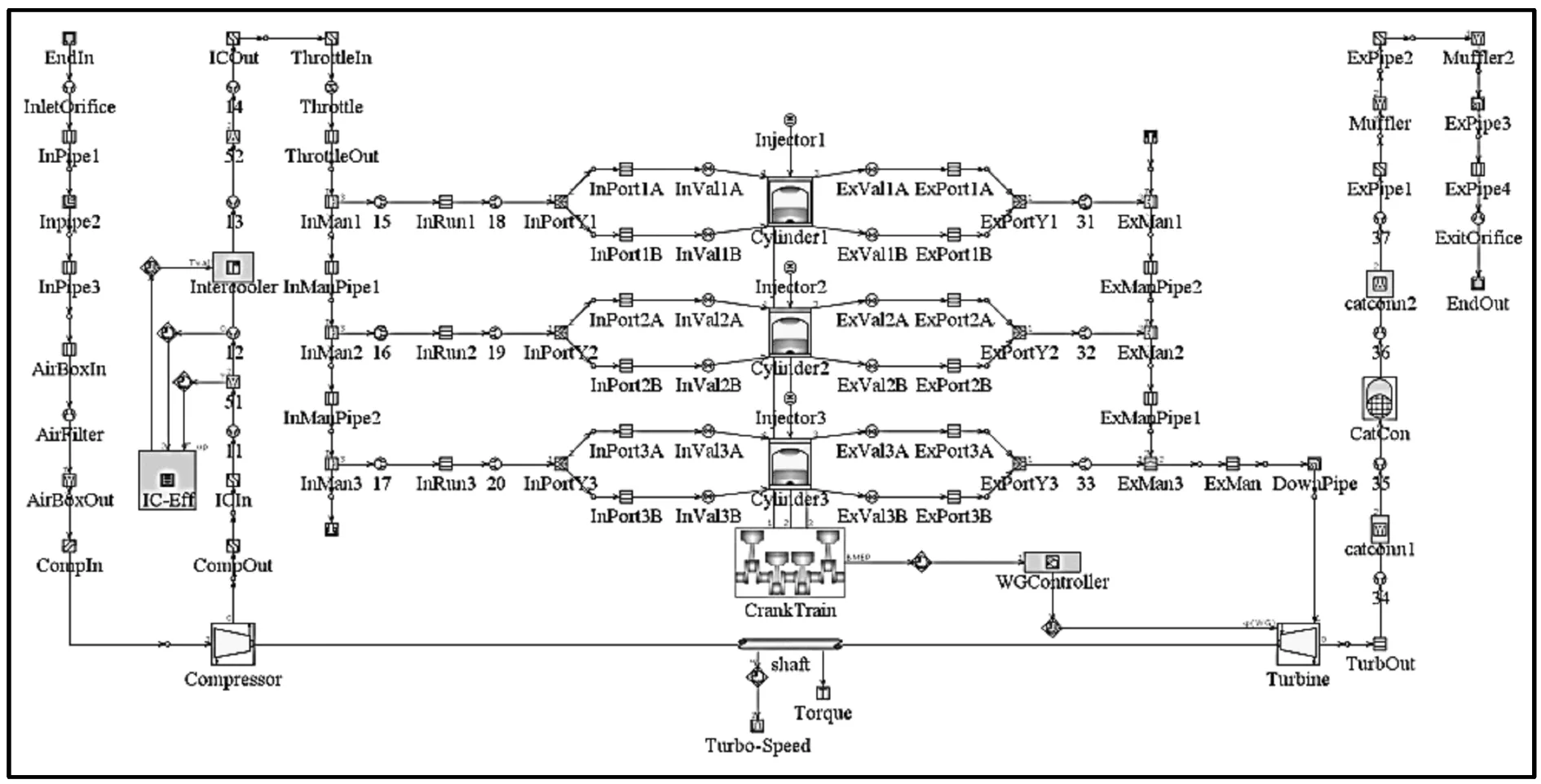
圖2 發動機工作過程仿真模型

1.3 計算模型驗證

為了保證原型發動機工作過程仿真模型的準確性，將發動機性能仿真結果與已知性能參數進行對比。采用特定工況下臺架試驗獲得的缸內燃燒壓力、燃燒放熱率、氣缸入口壓力、氣缸進氣溫度、氣缸排氣溫度、充氣效率、有效扭矩和有效燃油消耗率等性能參數，對發動機工作過程仿真模型進行了驗證。

圖3示出工況1發動機缸內燃燒壓力仿真數據與試驗數據的對比。圖4示出工況1發動機缸內燃燒放熱率仿真數據與試驗數據的對比。通過對比發現，缸內壓力以及燃燒放熱率的仿真與試驗結果基本一致，發動機燃燒模型的準確性得到了驗證。

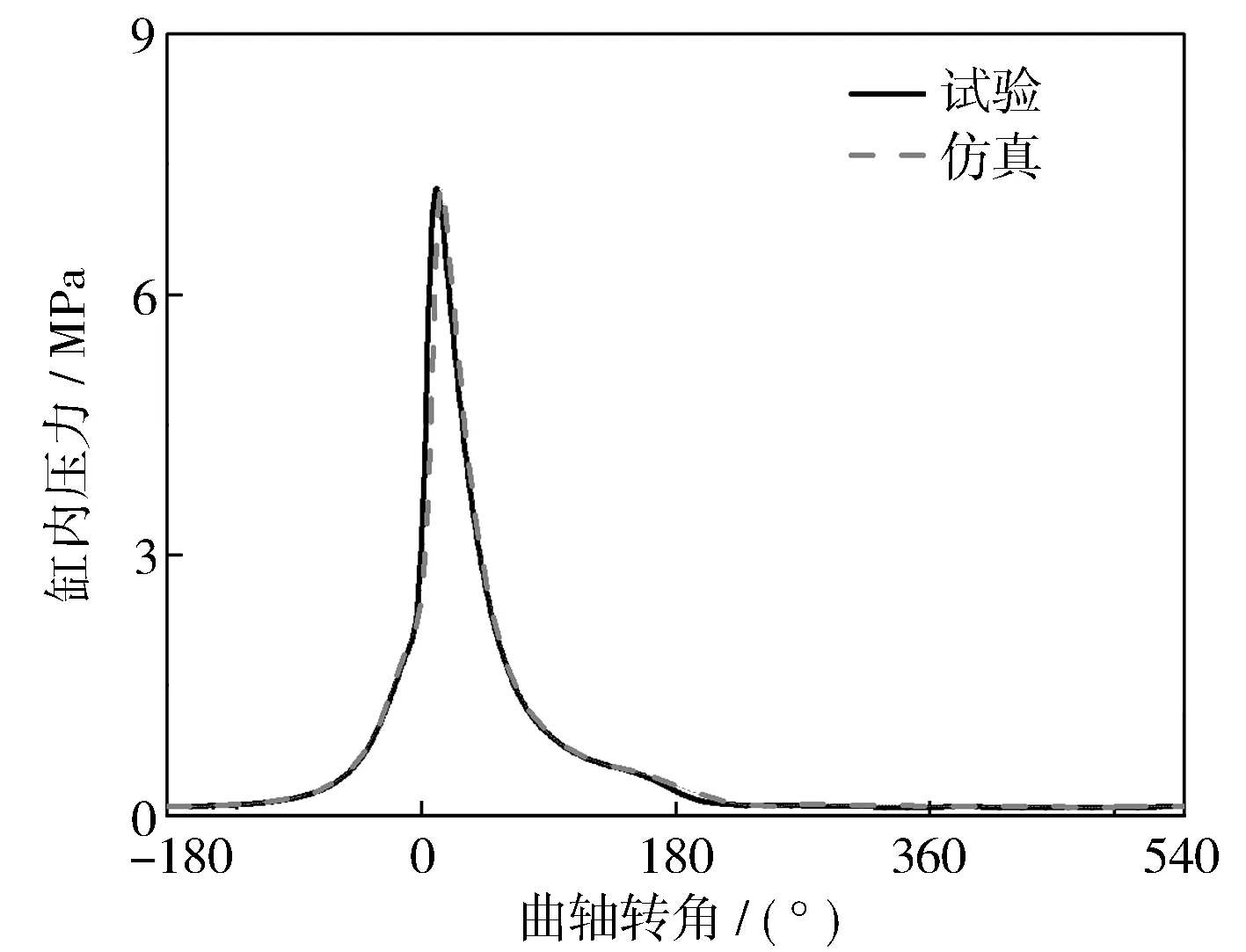
圖3 缸內燃燒壓力曲線對比

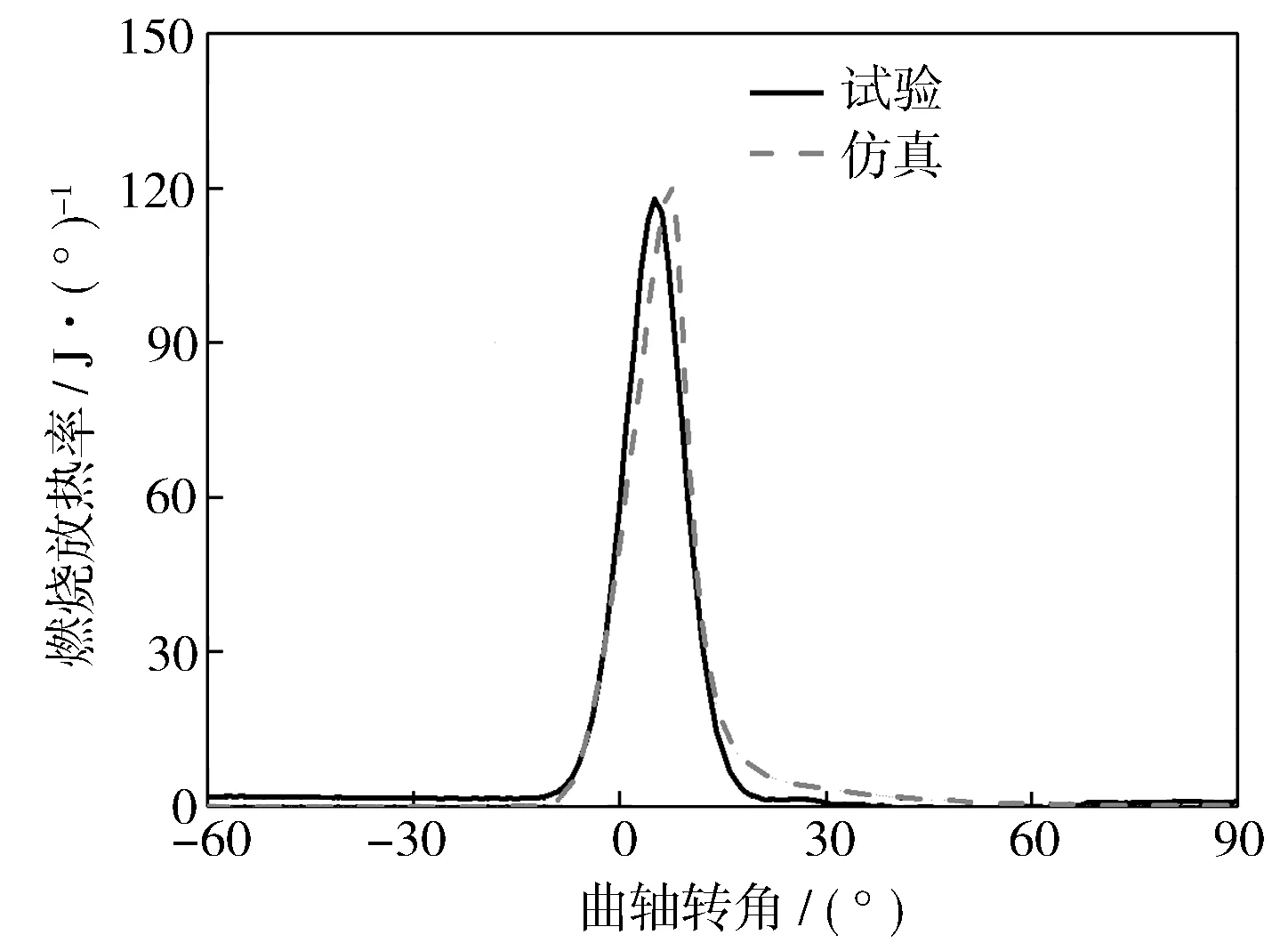
圖4 缸內燃燒放熱率曲線對比

對各工況的氣缸入口壓力以及氣缸進、排氣溫度仿真數據與試驗數據進行對比(見表3)，可以看出，試驗數據與仿真數據基本一致，氣缸入口壓力的最大相對誤差為0.82%，氣缸進氣溫度的最大相對誤差為1.23%，氣缸排氣溫度的最大相對誤差為2.76%，均小于3%，滿足驗證要求，缸內傳熱模型的準確性得到了驗證。

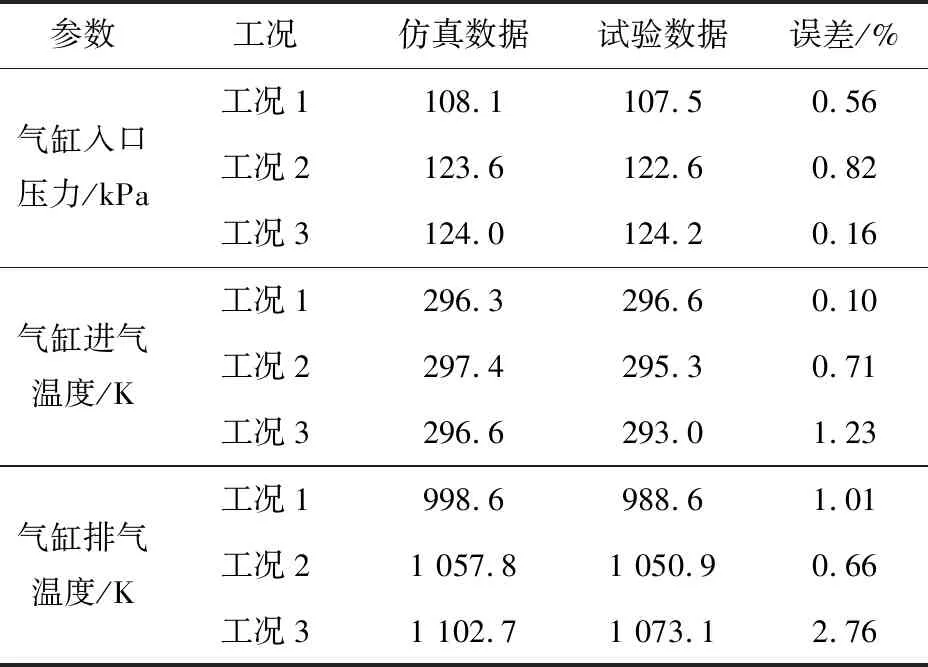
表3 氣缸入口壓力、進排氣溫度誤差對比

對發動機充氣效率、扭矩和燃油消耗率的仿真數據與試驗數據進行對比(見表4)，可以看出，試驗數據和仿真數據基本一致，充氣效率試驗數據和仿真數據的最大相對誤差為1.79%，扭矩試驗數據和仿真數據的最大相對誤差為2.01%，燃油消耗率試驗數據和仿真數據的最大相對誤差為1.47%，均小于3%，滿足驗證要求，工作過程模型可以較準確地反映原型發動機工作性能。

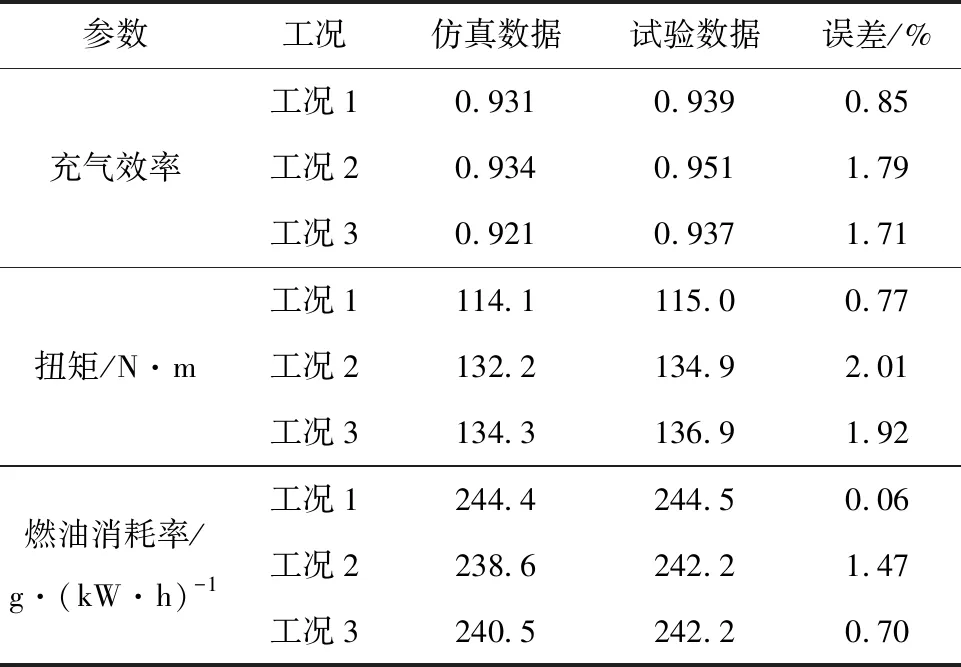
表4 充氣效率、扭矩、燃油消耗率誤差對比

1.4 爆震模型的標定

如果在發動機運行過程中采用高壓縮比技術，則需要考慮高壓縮比可能帶來的爆震現象。發動機的幾何壓縮比較高時，在正常燃燒火焰到來之前，端部混合氣體發生非正常燃燒，而且伴隨強烈的缸壓振蕩，從而引起爆震[8]。因此，在仿真模型中加入了爆震模型,用來預測爆震的發生。

GT-Power中的爆震模型基于阿累尼烏茲函數，采用自燃誘導時間積分計算公式來判斷爆震是否發生。自燃誘導時間積分計算公式為

(1)

式中：I為誘導時間積分；τ為誘導時間。當I(t)大于1時，即認為發生爆震。

模型中的誘導時間τ通過Douaud & Eyzat經驗公式[8]進行計算：

(2)

式中：P，A為與燃油物性有關的常數；ON為燃料辛烷值；p為瞬時缸內壓力；Tu為未燃氣體瞬時溫度。

爆震強度采用爆震指數(Knock Index)進行表示，在GT模型中調用爆震模塊進行計算，計算公式[7]如下：

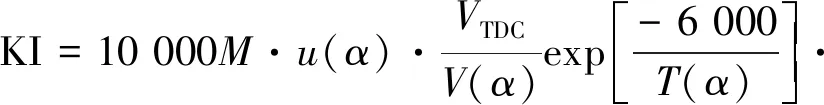
(3)

式中：M為爆震指數系數；u(α)為未燃氣體質量分數；VTDC為上止點燃燒室容積；V(α)為氣缸容積；Ф(α)為未燃區比例；Iave(α)為誘導時間積分。

在原型發動機臺架試驗中，通過爆震時的響度來判斷是否發生爆震[9-10]，原型發動機在2 000 r/min全負荷工況，點火時刻5.3°曲軸轉角時，產生輕微爆震現象。在爆震模型中，當誘導時間積分大于等于1時，認為發動機產生爆震現象。因此，在發動機2 000 r/min全負荷工況以及點火時刻5.3°曲軸轉角條件下，對KI值進行了標定。在該工況下，KI=80.13時與發動機輕微爆震相匹配，即認為KI<80.13時，發動機不發生爆震[11]。

另外，工況1、工況2和工況3下的KI值分別為46.7，23.7和15.3，均在爆震因子限值以下，不會發生爆震。

2 研究結果與分析

2.1 米勒循環對發動機燃油經濟性的影響

米勒循環技術有兩種實現形式：進氣門早關(EIVC)與進氣門晚關(LIVC)。其中LIVC間接實現了阿特金森循環，因此，LIVC形式的米勒循環也叫做阿特金森循環[12]。有研究表明，高負荷下LIVC形式能使燃燒相位更加優化、缸內燃燒更為充分，使得其燃油改善效果好于EIVC形式[6,13]。因此，本研究僅針對LIVC形式的米勒循環(阿特金森循環)進行分析。圖5示出LIVC形式的米勒循環氣門升程。保持進氣門開啟角不變，通過改變進氣門最大升程持續期實現進氣門晚關[13]。由圖5可知，進氣門開啟角不變，進氣門最大升程持續期每增加10°，進氣門關閉角會推遲10°，以此類推。下文所提到的米勒度(φLIVC)是指在原發動機進氣門關閉角基礎之上推遲的角度。

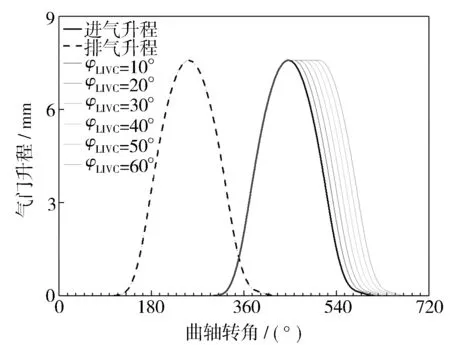
圖5 進氣門晚關形式的米勒循環氣門升程

分別在前文所述3個高熱效率工況點下改變米勒度，獲得了圖6所示的燃油消耗率隨米勒度的變化規律。由圖6可知，在不改變節氣門開度以及增壓壓力的前提下，3個工況下的燃油消耗率隨著米勒度的增大而逐漸增大。

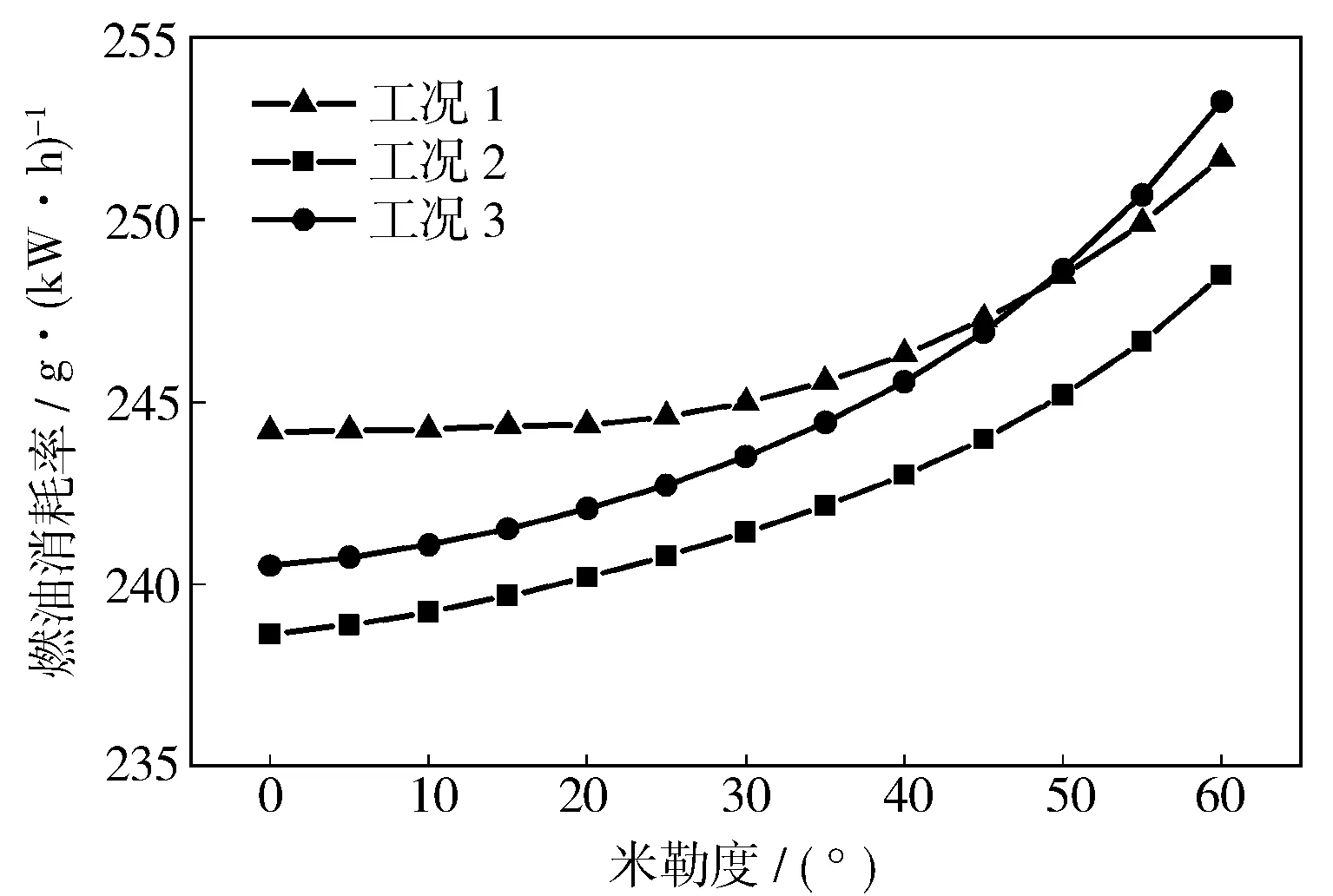
圖6 燃油消耗率隨米勒度的變化規律

圖7示出工況1有效壓縮比隨米勒度的變化規律。在幾何壓縮比不變情況下，有效壓縮比隨著米勒度的增大而減小，循環熱效率下降，導致燃油消耗率上升。圖8示出工況1不同米勒度下的進氣質量流量。米勒度增大后，活塞從下止點上行過程中會將部分進氣推回進氣道，產生如圖8所示的進氣回流現象，氣缸累計進氣量減少，充氣效率下降[14]。

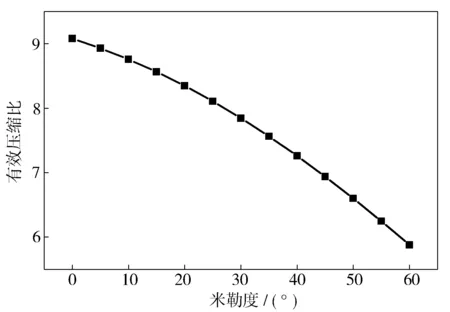
圖7 工況1有效壓縮比隨米勒度的變化規律

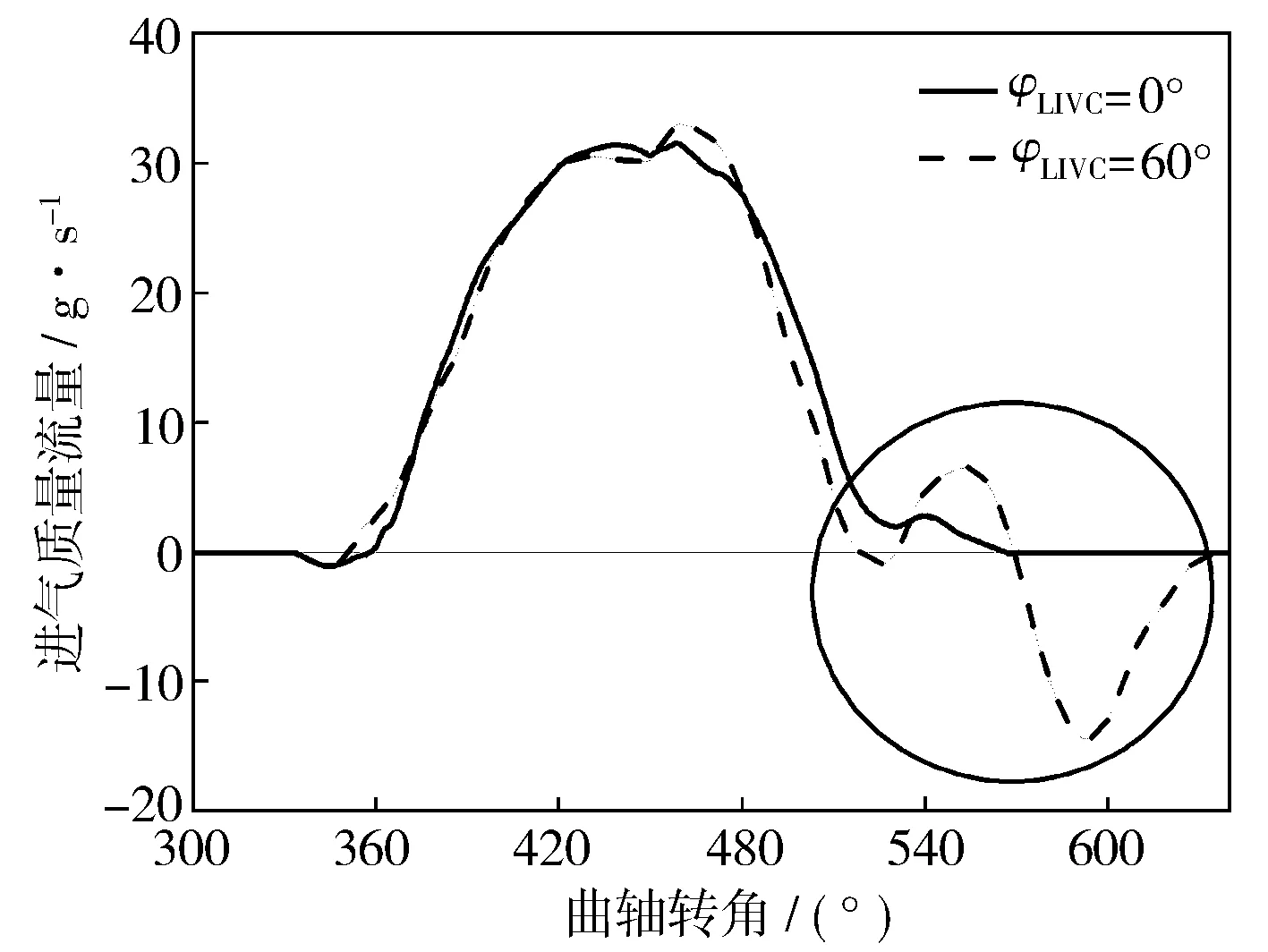
圖8 工況1不同米勒度下的進氣質量流量

2.2 高壓縮比對發動機燃油經濟性的影響

提高壓縮比的主要措施有兩種：第一種是通過增加發動機活塞行程，提高發動機幾何壓縮比；第二種是通過減少燃燒室容積，提高發動機幾何壓縮比。若改變活塞行程，發動機排量會相應改變，所以本研究采用第二種措施，通過減少燃燒室容積提高發動機幾何壓縮比[3]。表5示出采用第二種措施時壓縮比、燃燒室容積和排量的對應關系。

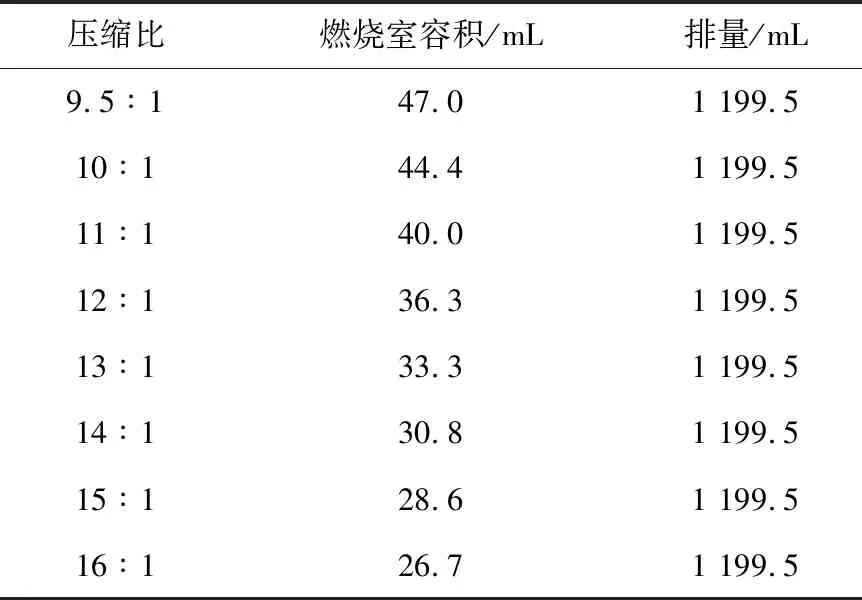
表5 壓縮比、燃燒室容積和排量的對應關系

通過調整點火時刻，將爆震因子限制在80.13以內。圖9示出了3個工況下燃油消耗率隨壓縮比的變化規律。

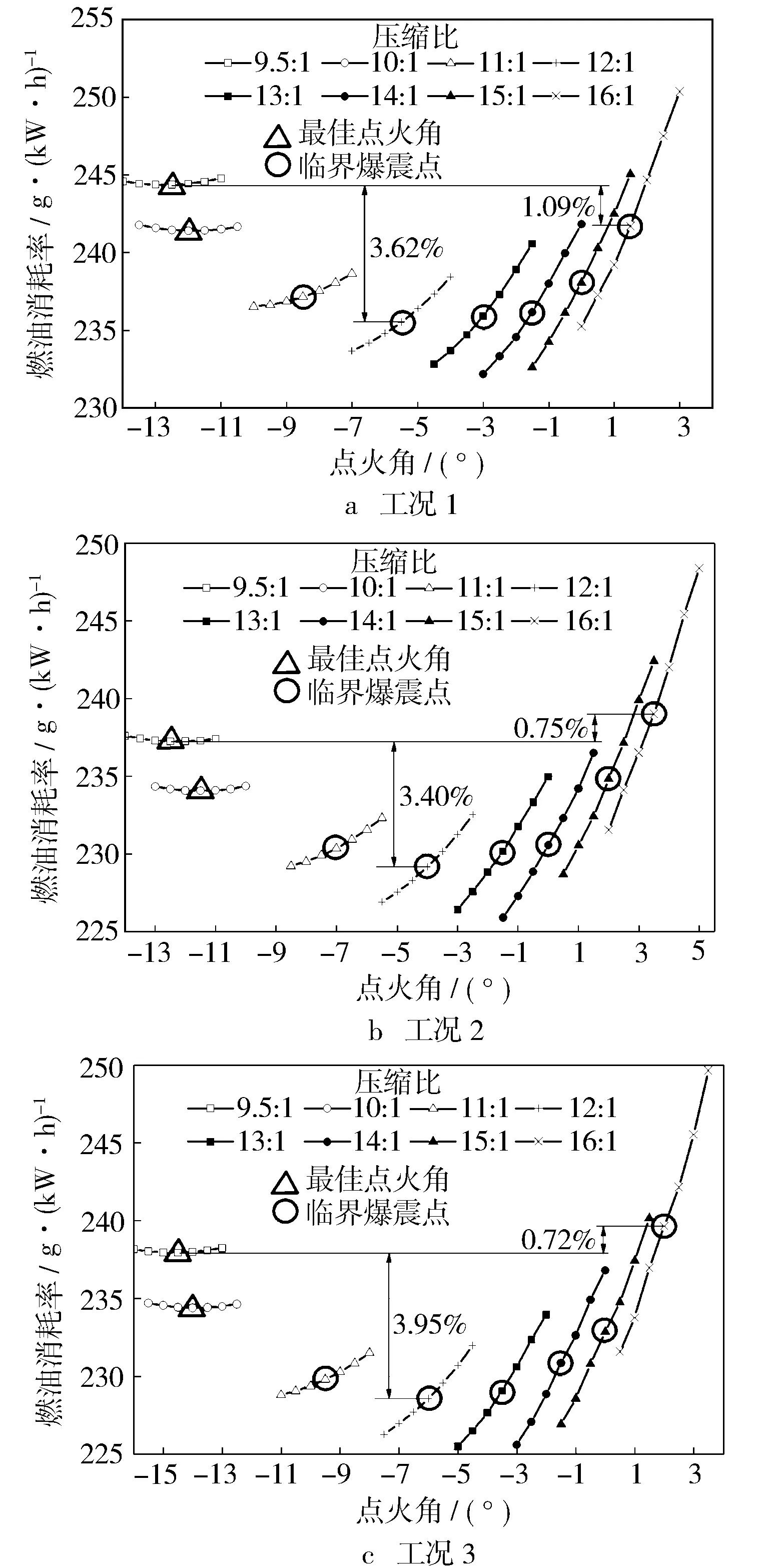
圖9 臨界爆震點和最佳點火角下燃油消耗率隨壓縮比的變化規律

通過圖9發現，隨著壓縮比的提高，3個工況下的燃油消耗率均呈現先減小后增大的趨勢。通過分析可知，幾何壓縮比直接影響發動機的理論熱效率，隨著壓縮比的提高，燃油消耗率下降，但繼續提高壓縮比，爆震現象越來越嚴重，如果通過被迫推遲點火時刻的方式來抑制爆震，會導致燃油消耗率大幅上升。如圖9所示，在原機壓縮比9.5∶1和壓縮比10∶1時，均在最佳點火時刻獲得最低的燃油消耗率，由此可以看出，將壓縮比提高到10∶1時，3個高效率工況下均不會發生爆震現象，而從壓縮比11∶1開始，需要推遲點火時刻來抑制爆震。除此之外，對比每個工況下燃油消耗率可發現，工況3下，壓縮比為12∶1時的燃油消耗率相比于原機下降幅度最大，下降了3.95%，可達到228.54 g/(kW·h)。工況1下，壓縮比為16∶1時的燃油消耗率比原機下降了1.09%；工況2和工況3下，壓縮比為16∶1時的燃油消耗率相比于原機分別上升了0.75%和0.72%。

2.3 米勒循環與高壓縮比間相關性分析

在圖9中每個工況最低燃油消耗率所對應的點火時刻下，對米勒循環與高壓縮比間的相關性進行分析。其中，工況1對應的點火角為-5.5°，工況2對應的點火角為-4°，工況3對應的點火角為-6°。利用徑向基函數法[15]獲得了如圖10所示的米勒度與幾何壓縮比的燃油消耗率等高線圖，圖中虛線代表爆震因子KI=80.13的等高線，即爆震臨界曲線，不發生爆震區域均位于爆震臨界曲線左側。

由圖10可知，3個高效率工況下米勒度與壓縮比對燃油消耗率變化影響趨勢基本一致。由圖10a可以看出，隨著壓縮比的提高，燃油消耗率下降，但下降趨勢逐漸放緩；隨著米勒度的增加，燃油消耗率上升，上升趨勢從30°曲軸轉角后才逐漸明顯。隨著米勒度的增加，爆震臨界曲線所對應的壓縮比越來越大，即不發生爆震區域可以包含越來越高的壓縮比。基于以上分析可知，在點火角不變的前提下，提高壓縮比可以大幅降低燃油消耗率，但與此同時帶來嚴重的爆震影響，米勒循環的加入可以在小幅提高燃油消耗率的同時，有效地降低高壓縮比帶來的爆震影響。

由圖10中各工況的爆震臨界曲線可知，米勒度為60°曲軸轉角時，工況1不發生爆震的最高壓縮比可達到15∶1，工況2不發生爆震的最高壓縮比可達到15.3∶1，工況3不發生爆震的最高壓縮比可達到16∶1，15∶1是3個工況均能達到的幾何壓縮比。因此，在原型發動機基礎上將幾何壓縮比調整為15∶1，米勒度調整為60°曲軸轉角進行仿真計算。圖11示出原型發動機與采用米勒循環以及高壓縮比的發動機對比結果。通過圖11對比結果可知，采用米勒循環以及高壓縮比技術可以有效降低發動機燃油消耗率。對于3個高熱效率工況，在米勒度60°曲軸轉角和壓縮比15∶1的條件下，燃油消耗率平均下降了5.21%。

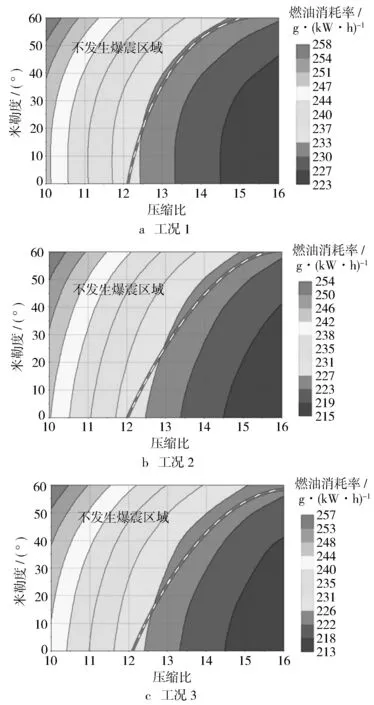
圖10 米勒度與壓縮比的燃油消耗率等高線圖

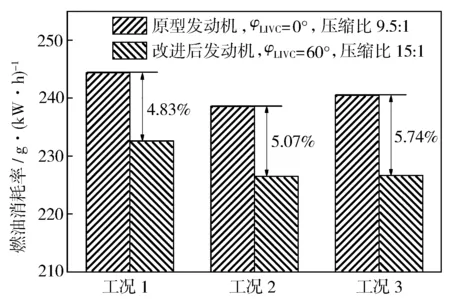
圖11 原型發動機與采用米勒循環以及高壓縮比發動機的燃油經濟性對比

3 結論

a) 單獨采用LIVC形式的米勒循環技術時，活塞上行過程中將部分進氣推回進氣道，導致充氣效率下降，有效壓縮比減小，從而降低了發動機燃油經濟性；

b) 單獨采用高壓縮比技術時，由于爆震影響，被迫推遲點火，可以在壓縮比為12∶1時獲得較低的燃油消耗率，但隨著壓縮比進一步提高，燃油消耗率升高；

c) 米勒循環技術與高壓縮比技術間在抑制爆震方面有較強的相關性，在提高發動機幾何壓縮比來改善燃油經濟性的同時，有必要采用米勒循環技術抑制爆震現象的發生；

d) 通過仿真計算可知，對于原型發動機高熱效率工況來說，在米勒度60°曲軸轉角和壓縮比15∶1的條件下，燃油消耗率平均下降了5.21%。