碳/石英防熱復合材料燒蝕性能

趙小程 楊凱威

（北京航天長征飛行器研究所，北京 100076）

文 摘 為研究碳/石英防熱復合材料的燒蝕性能，采用電弧加熱器和碳/石英平頭駐點模型，在不同駐點壓力Ps、不同熱流密度q和不同焓值hs的多組合條件下進行了燒蝕試驗。針對試驗所得數據，利用多元回歸分析方法，建立了質量燒蝕率與熱流密度、駐點壓力、焓值3個參數之間的數學模型，并對模型的合理性進行了檢驗。結果表明，所建立的3個參數數學模型對試驗數據的擬合程度很好，熱流密度與質量燒蝕率最為相關；與單參數、2個參數的數學模型相比，3個參數的數學模型對實驗數據的擬合效果更好，能很好地反映碳/石英防熱復合材料的燒蝕性能。

0 引言

近年來，隨著航空航天、原子能、先進飛行器及材料冶煉技術的不斷提升，國內外對于先進耐高溫、耐燒蝕復合材料提出了更加苛刻的要求。陶瓷基防熱復合材料（CMC）克服了傳統陶瓷材料脆性大的缺點，具有耐高溫、抗燒蝕、高溫力學性能優良等優點。當前，美國、日本及歐洲等國家為了保持高技術陶瓷基復合材料（CMC）的優勢，投入了大量的人力物力進行陶瓷基防熱復合材料（CMC）的研究與開發，目前已進入應用階段[1]。比如，X系列飛行器的頭錐、翼緣等極高溫區域熱防護結構就采用了陶瓷基復合材料[2]。還有，目前美國開發的高超聲速航空飛行器（如獵鷹無人駕駛高超聲速試驗飛行器HTV-2），對空氣動力學提出來更高的要求，它們均有尖銳的前緣，這些部位對材料的要求更為苛刻，一般會用到超高溫陶瓷基復合材料來對其進行熱防護[3]。圖1給出了碳/石英材料的微觀形貌。碳纖維在惰性氣體中，即使在2 000℃以上的高溫，其強度和彈性模量的變化也很小，在航天、飛行器等瞬間或短時高溫領域具有很重要的實際使用意義[4-5]。碳纖維與石英線脹系數相當，二者復合過程中使用的石英基體對碳纖維具有良好的浸潤性，在性能與制造工藝上匹配性良好。應用碳纖維增強石英基體，可以使材料具有較高的承載能力、抗沖擊能力、抗熱震能力，優良的抗燒蝕性能及防熱性能，在高溫環境下可以保持較穩定的物理化學性質。目前，碳/石英防熱復合材料在國內已經有了較為深入的研究，已應用到飛行器中。

圖1 碳/石英防熱復合材料微觀形貌Fig.1 Microscopic morphology of carbon/quartz heat-resistant composites

材料的燒蝕性能與熱環境參數密切相關。梁歡等[6]研究了硅基材料有效燒蝕與焓值和壓力的關系，并給出了相應的數學模型，周燕萍等[7-8]給出了CF/S-157PF復合材料有效燒蝕焓或質量燒蝕速率與熱流密度和燒蝕時間之間的關系式。二者研究的均為2個熱環境參數（壓力、焓值）或1個熱環境參數（熱流）對材料燒蝕性能的影響，未研究熱流密度、壓力、焓值3個參數同時作用下對復合材料質量燒蝕率的影響以及關系式。碳/石英作為一種性能優良的陶瓷基防熱復合材料（CMC），國內外對其在不同熱環境條件下的燒蝕性能報道文獻很少。本文以碳/石英防熱復合材料制成的駐點模型為研究對象，采用管狀電弧加熱器設備完成不同駐點壓力Ps、不同熱流密度q和不同焓值hs的多組合條件下該材料燒蝕試驗。然后，依據碳/石英防熱復合材料的駐點燒蝕試驗數據，利用回歸分析方法研究熱流密度、駐點壓力、焓值與質量燒蝕率之間的影響規律。

1 實驗

1.1 設備及模型

管狀電弧加熱器：一種自由弧長的電弧加熱器，其前后電極呈管狀。

試驗模型：由碳/石英防熱復合材料制成的駐點模型，其直徑為25～30 mm，高30～40 mm。試驗過程中采用紅外測溫儀對駐點表面溫度進行測量。

1.2 實驗方案

圖2為試驗裝置示意圖。安裝時，將模型的軸線安裝在電弧加熱器的中心線上，并使模型截面平行于噴管出口截面，這樣可以保證模型燒蝕均勻。然后，按圖示位置及方法布置好紅外測溫儀。熱流、壓力采用直接測量的方法對外形尺寸相同的試驗模型在不同狀態下進行測量，氣流的焓值通過總壓流量法計算獲得，材料的質量燒蝕率用稱重法測得。正式試驗前首先進行流場調試，經過流場調試后，便可進入正式試驗。

圖2 設備及模型安裝示意圖Fig.2 Installation figure of equipment and model

1.3 結果與分析

共進行50余次試驗，試驗條件及各個試驗條件下的質量燒蝕率見表1。圖3為不同系列典型狀態下材料模型燒蝕后形貌。可以發現，模型在表1試驗條件下均發生了燒蝕，燒蝕表面基本保持平坦，燒蝕面形成了白色燒蝕產物即熔融液態層。在較低狀態下，液態層附著在燒蝕面，較高狀態下液態層在剪切力和壓力作用下被吹至模型柱面，高狀態下，液態層被直接吹掉。

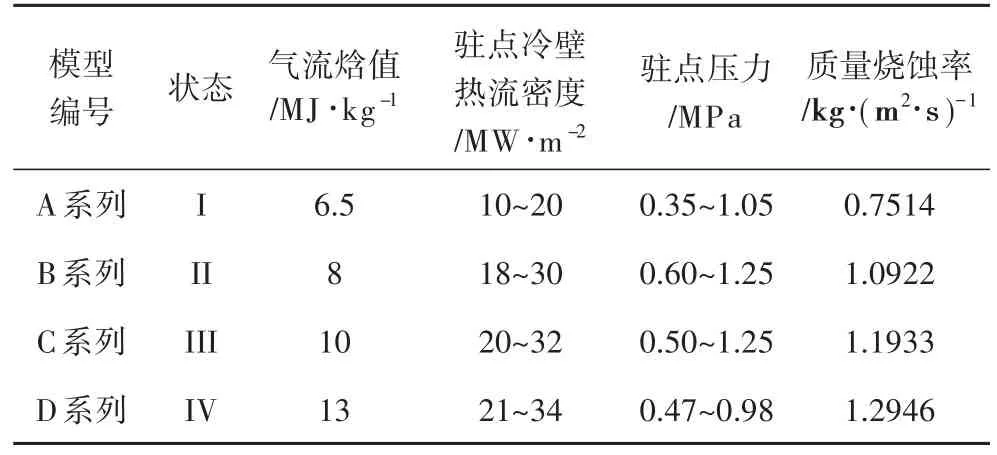
表1 試驗參數記錄Tab.1 Value of experimental parameters

圖3 模型燒蝕后形貌Fig.3 Models'morphology after ablation

在文獻[6]的研究結果基礎上，提出了質量燒蝕率與熱流、壓力和焓值三參數相關聯的指數數學模型，具體表達式為：

將（1）式兩端同時取對數，得到（2）式如下：

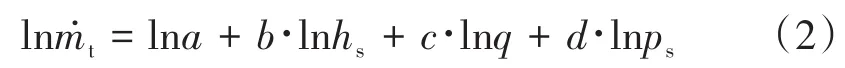
要確定出（1）式中的系數，只需通過多元線性回歸方法求出（2）式便可。

多元線性回歸分析的數學模型為：

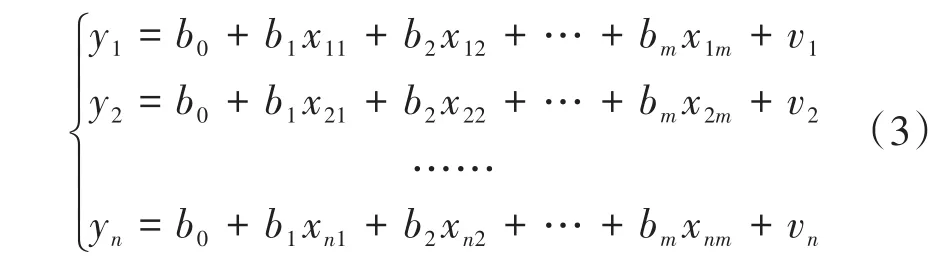
（3）式中待求系數有m+1個，而方程式的個數有n個，對于精密測量，一般要求測量次數n＞m+1，這樣（3）式構成了矛盾方程組無法求解。為了解決此問題，采用最小二乘原則[9]，用表達式表述為：

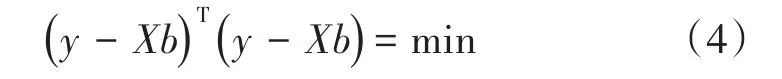
使用matlab軟件進行回歸計算，得到多元線性回歸方程為：

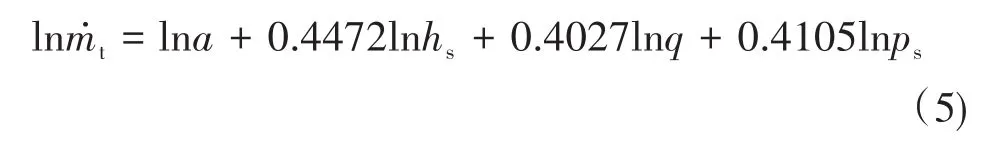
將（6）式中系數回代到（1）式中，得到最終確定出來的數學模型為：

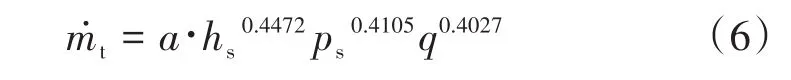
圖4給出了試驗數據的散點分布及擬合直線。擬合直線方程為y=1.005x，近似與直線y=x重合，可以看出，式（6）的擬合效果很好。

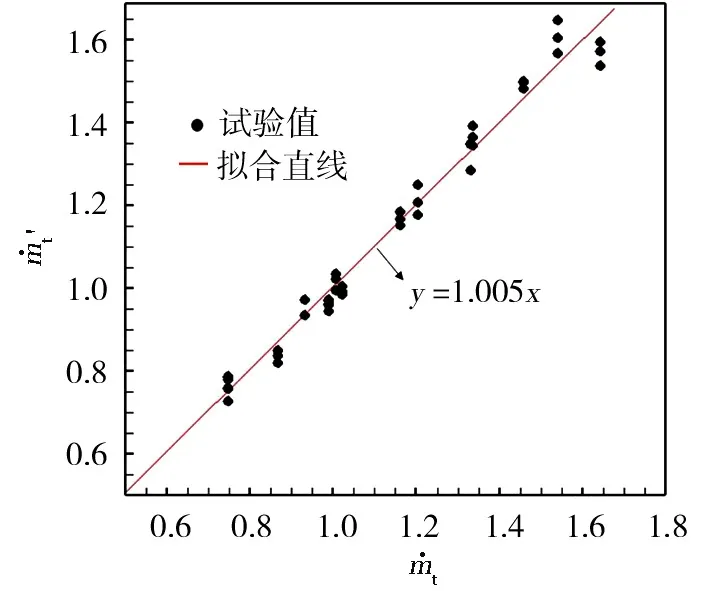
圖4 散點及擬合直線圖Fig.4 Scatter point and fit line graph

針對以上模型進行相關性、擬合優度、方程顯著性、變量顯著性檢驗。

（1）變量間相關性檢驗

皮爾森相關系數是用來反映兩個變量線性相關程度的統計量[10]。皮爾遜相關系數計算表達式為：

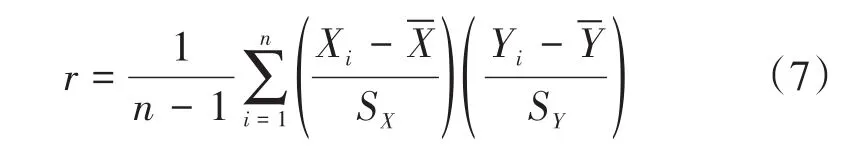
（2）擬合優度檢驗

為了檢驗描述碳/石英材料質量燒蝕率的多元線性回歸方程與數據的擬合程度，可以采取擬合優度檢驗的方法來說明[10]。擬合優度檢驗方法需要構造一個可以表征擬合程度的指標R2。統計量R2定義為：

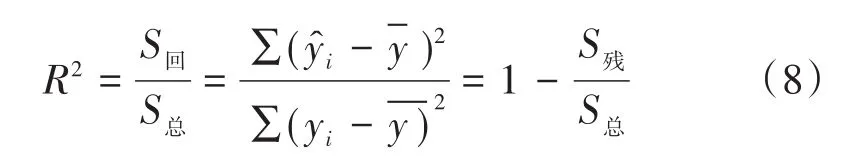
式中，S總為總變差平方和，S殘為殘差平方和，S回為回歸平方和。

（3）回歸模型顯著性檢驗

通過計算統計量F值來說明總體上被解釋變量與解釋變量之間的線性關系是否顯著[10]。其中，統計量F定義為：

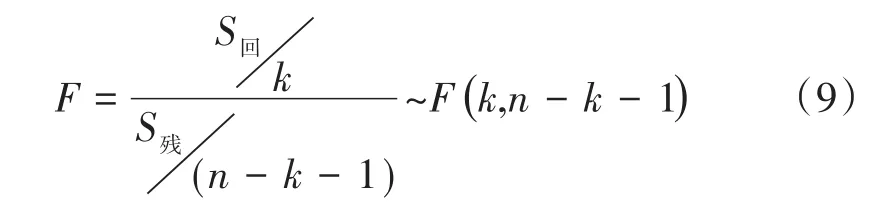
（9）式說明，統計量F服從自由度為(k，n-k-1)的F分布。通過查詢F分布統計表，便可以得出在特定顯著性條件下F檢驗的臨界值。當統計量F的值大于臨界值時，即可認為在總體上自變量與質量燒蝕率之間呈顯著的線性關系。

（4）回歸系數的顯著性檢驗

回歸模型的顯著性檢驗是從總體上對方程的線性關系進行檢驗，然而，實際上可能會有個別因子對質量燒蝕率沒有影響或影響不顯著。從應用的角度看，應該設法找出這些影響不顯著的因子，并將其從回歸方程中剔除。采用回歸系數的顯著性檢驗定義統計量Fj為：

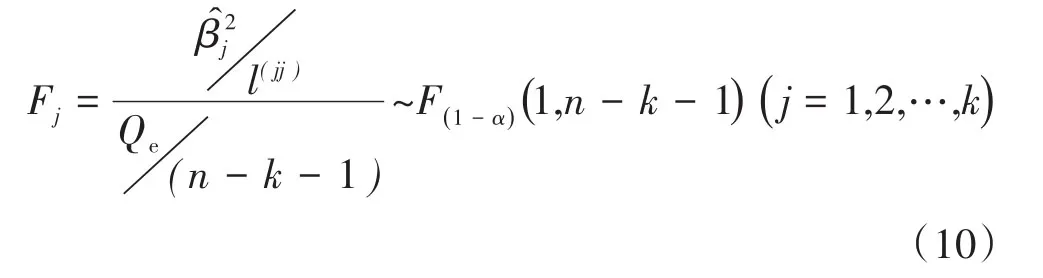
對于給定的顯著性水平α，當檢驗統計量

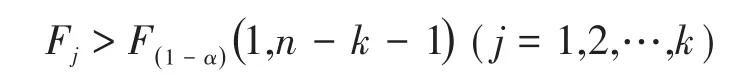
則認為所研究的影響因子是顯著的[7]。

1.4 檢驗結果

相關系數計算結果如表2所示。其中Xi為lnhs、lnps和 lnq所代表的樣本數據，Yi為 lnm˙t所代表的樣本數據。由計算結果可以看出，自變量lnhs、lnps與因變量 lnm˙t的相關系數r值為 0.40～0.69，可以認為氣體焓值、駐點壓力與碳/石英質量燒蝕率之間中度相關；自變量lnq與因變量lnm˙t的相關系數r值為0.7～1.0，認為駐點冷壁熱流密度與材料質量燒蝕速率高度相關。結果表明，建立（6）式這樣的數學模型滿足相應精度要求。

由表3看出，擬合優度檢驗的計算結果為R2=0.9823＞0.95，說明數學模型的擬合效果很好；回歸模型顯著性檢驗的F=759.8396，說明回歸模型的顯著性良好；且概率值P＜0.001 0，總回歸方差為0.001 1，這些都充分說明了所建立的數學模型對試驗數據的擬合程度很好。

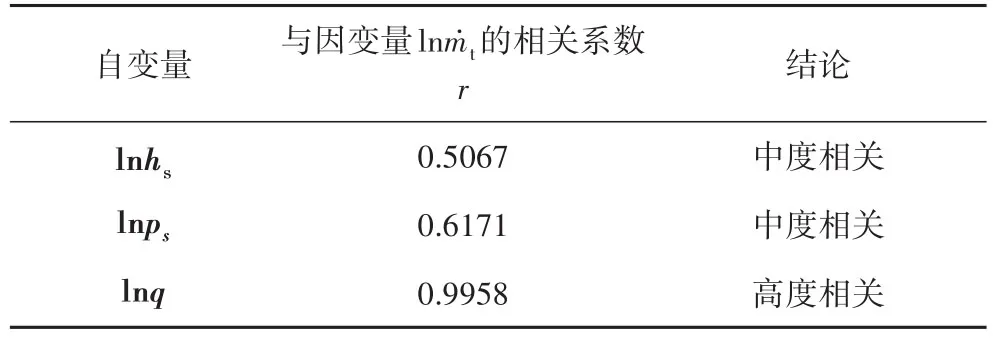
表2 相關系數計算結果表Tab.2 Calculation value of relativity coefficients

表3 模型檢驗結果Tab.3 Model test results

表4給出了回歸系數的顯著性檢驗結果，結果表明，3個回歸系數的顯著性都很好，其中駐點壓力最為顯著。

表4 回歸系數的顯著性檢驗結果Tab.4 The significance test results of regression coefficients

1.5 3個參數模型與單參數、2個參數模型對比

將擬合所得的3個參數數學模型與單參數、2個參數數學模型進行對比，結果如表5所示。

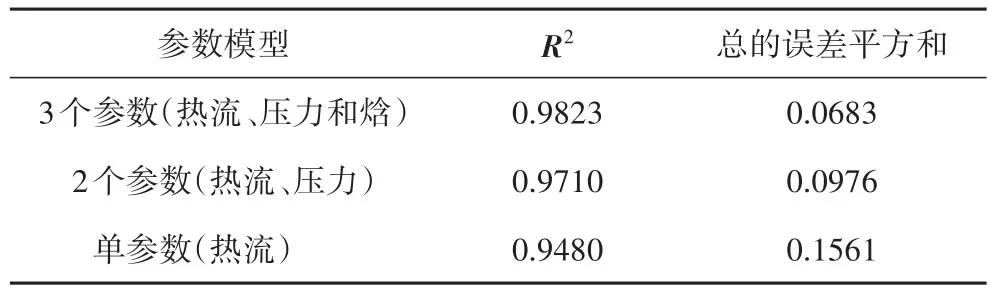
表5 3個參數模型與單參數、2個參數模型對比Tab.5 Comparison of three parameter model with one parameter and two parameter models

從表5可以看出，3個參數數學模型與單參數、2個參數數學模型相比，對實驗數據的擬合效果最好，計算所得到的總的誤差平方和也最小，能更好地反映碳/石英防熱復合材料的燒蝕性能。

2 結論

（1）提出了質量燒蝕率與熱流、壓力、焓值3個參數相關的數學模型，并采用數學方法回歸出了模型中的各相關系數，得到了具體的關系式。并對數學模型進行了一系列檢驗，其中，擬合優度檢驗結果為R2=0.982 3，回歸模型顯著性檢驗結果為F=759.839 6，總回歸方差為0.001 1，回歸系數的顯著性檢驗表明3個回歸系數都很顯著。

（2）研究了3個參數對質量燒蝕率的相關性，結果表明質量燒蝕率與熱流高度相關，其次是焓值和壓力。

（3）將擬合所得的3個參數數學模型與單參數、2個參數數學模型進行對比。結果表明3個參數的數學模型對實驗數據的擬合效果最好，能更好地反映碳/石英防熱復合材料的燒蝕性能。