虹橋式木拱橋結構力學特性分析

孟雨澤, 宋郁民，王思穎，張泰源

(上海工程技術大學 城市軌道交通學院, 上海 201620)

木材具有取材容易，加工方便，重量輕，強度較高，抗震性能較好的優點，相較于石材，木材重量極輕，是建造橋梁最原始的材料之一[1-3]。其中，木拱橋在我國古代橋梁史占有極其重要的地位，它以獨特的編木拱結構，利用兩個縱橋向的拱肋系統相互交替有組織的編制在一起，再輔以若干橫橋向的橫木聯結組成，形成拱形結構，實現了較大的跨度，且直木無需彎曲，節點處無需借助金屬材料輔助連接，結構精巧，受力合理，施工簡單[4-7]。然而，目前對虹橋式木拱橋的結構受力性能方面的研究較少，本文以一座虹橋式木拱橋為例，通過改變其拱肋的矢跨比、節間數和截面尺寸，分別建立與之相對應的有限元模型，并將有限元模型中的計算結果進行對比分析，研究上述三個因素的變化對于虹橋式木拱橋結構力學特性的影響。

1 工程背景

1.1 工程背景簡介

該虹橋式木拱橋全長11.4 m，橋寬為2.1 m，橋面及欄桿向兩側路基延伸，全長21.6 m，主拱結構凈跨徑為9.584 m，凈矢高為1.55 m，矢跨比為1/6.18，橋下正常水位-0.400 m。原橋型見圖1。

該木拱橋的拱肋結構由兩個系統相互交叉編織而成，并輔以橫木，使兩系統緊密結合，構成橋梁主拱結構的拱肋彼此之間用鉚釘連接，既保證了一定的強度，也便于日后的維護修理，同時結構形式優美而流暢。原橋梁編木拱結構設計圖見圖2。

圖1原橋型布置圖(單位：mm)

圖2編木拱結構設計圖(單位：mm)

本文以此木拱橋為原型，在原橋橋面板和欄桿等設施不變的情況，通過改變拱肋的矢跨比、節間數和截面尺寸，來研究編木拱結構最大應力和最大撓度的變化規律，以及在極限承載能力下，結構所能承受的最大荷載的變化規律。

1.2 材料特性和設計強度

木橋全橋均采用俄羅斯樟子松，根據《木結構設計規范》[8](GB 50005—2003)，查得俄羅斯樟子松的木材強度等級屬于TC13B，彈性模量E=9 000 MPa，順紋抗壓及承壓極限為10 MPa，順紋抗拉極限為8 MPa，抗彎強度設計值為13 MPa，泊松比取0.3，木材的質量密度取540 kg/m3。

2 力學特性分析

2.1 結構建模

拱肋結構采用MIDAS/Civil空間有限元程序進行建模驗算，拱肋結構采用梁單元進行模擬。木材為各性異向材料，要精確模擬其材料的本構關系比較困難，此處我們只研究其縱向受力系統，因此用自定義各向同性材料來模擬俄羅斯防腐木材[1]。

拱腳用固定鉸支座模擬，即約束三個線位移Dx、Dy、Dz，釋放三個角位移Rx、Ry、Rz。拱肋與橫梁之間采用鉚釘連接，用彈性連接來進行模擬[1，9-10]，彈簧剛度根據靜載試驗結果進行修正[1]。用較大的線剛度來約束y方向和z方向的線位移，用較小的線剛度來約束x方向的線位移；對拱肋與橫梁x方向與z方向的轉動剛度進行約束。因為不改變原橋的橋面板和欄桿等設施，所以將拱肋結構以上的結構自重(包括橋面板和護欄等附屬設施)加上人群荷載以外荷載的形式作用在拱肋節點上。彈性連接具體取值見表1。

表1 拱肋與橫梁彈性連接具體取值

(1) 矢跨比。根據工程背景，固定了虹橋式木拱橋拱肋結構跨度L=9.6 m，改變其矢跨比H/L，即改變拱肋結構的矢高H。本文分析研究四種不同矢跨比的模型，即矢跨比分別為1/6、1/5、1/4、1/3。因拱肋節點不隨矢跨比的改變而發生變化，所以經計算不同矢跨比采用相同的節點荷載，即32.892 kN。各矢跨比參數見表2。

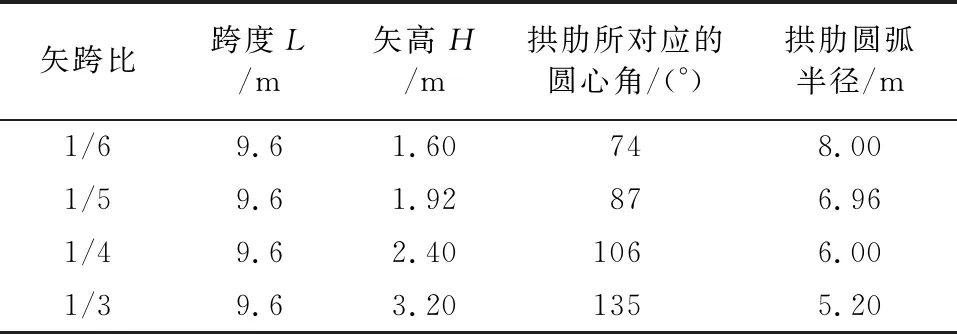
表2 不同矢跨比參數

(2) 節間數。為了增強不同節間數有限元模型的可比性與準確性，本文選用相同的矢跨比H/L=1/4，來討論五種不同的節間數，即節間數分別為五節拱、六節拱、七節拱、八節拱和九節拱[11]。因節間數的改變，使得拱肋結構中的節點數也隨之變化，有限元模型中對應的節點荷載也隨之改變。不同節間數所受節點荷載見表3。

表3 不同節間數所受的節點荷載

(3) 拱肋截面。為了增強不同拱肋截面有限元模型的可比性與準確性，本文選用矢跨比H/L=1/4和七節拱來討論四種不同的截面尺寸，各截面尺寸見表4。

表4 不同截面尺寸

(4) 荷載組合。采用承載能力極限組合：1.2(自重)+1.2(二期)+1.4(人群)

2.2 矢跨比分析

2.2.1 強度分析

在承載能力極限組合作用下，不同矢跨比所對應的拱肋最大應力值見表5。

表5 不同矢跨比所對應的拱肋最大應力值

不同矢跨比所對應的拱肋應力圖如圖3、圖4、圖5所示，不同矢跨比所對應的拱肋最大應力值的變化圖如圖6所示。

由上述計算結果比較，可以發現：隨著拱肋結構矢跨比的增大，構件內最大應力值逐漸減小。

根據夾角與矢跨比的關系中可知：因為木拱橋結構由桿件相互搭接而成，在節點處的內力平衡需要滿足桿件的幾何關系，而內力主要有拱肋承擔，那么拱肋與外力之間的夾角越大，拱肋內部產生的軸力也就越大[8]，故隨著矢跨比的增大，拱肋節點處的角度變小，拱肋內部所產生的最大壓應力也隨之變小。

圖31/6矢跨比對應的拱肋應力圖

圖41/4矢跨比對應的拱肋應力圖

圖51/3矢跨比對應的拱肋應力圖

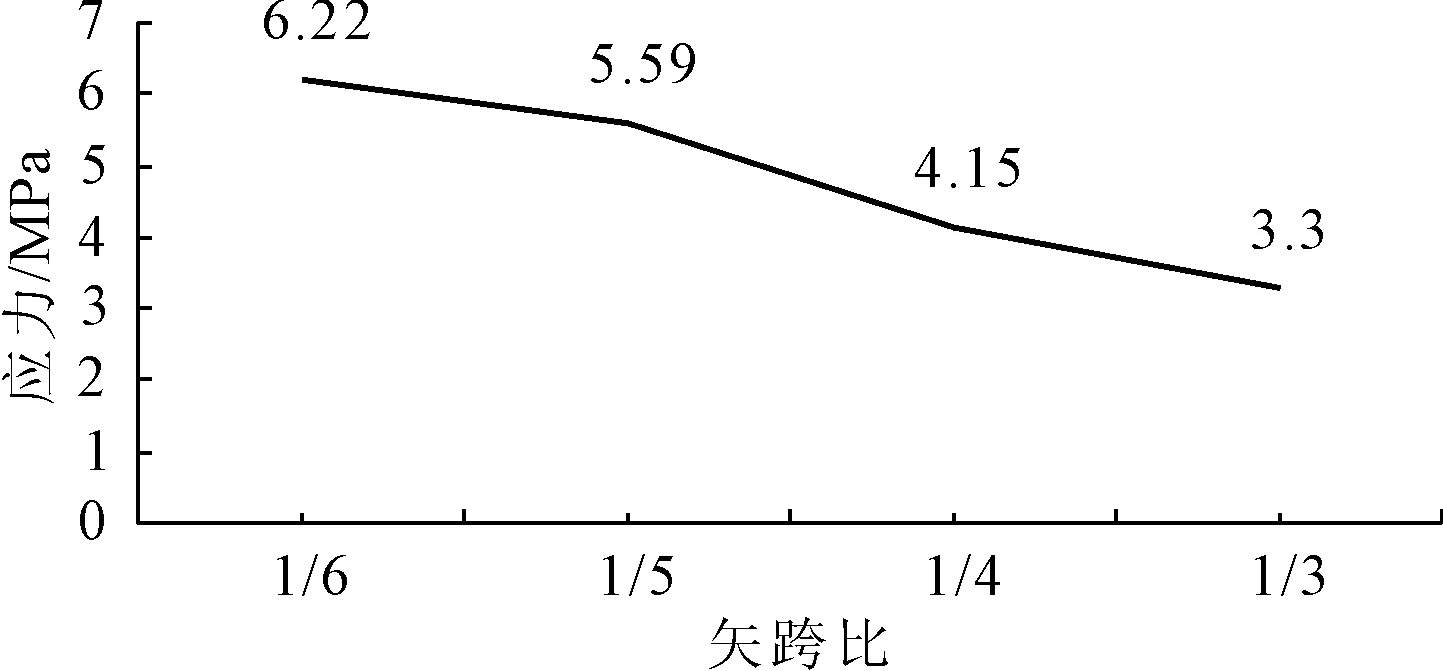
圖6不同矢跨比對應的拱肋結構最大應力變化圖

2.2.2 撓度分析

在承載能力極限組合作用下，不同矢跨比所對應的拱肋豎向撓度最大值見表6，表中豎向位移數值以豎直向下為正。

表6 不同矢跨比所對應的拱肋豎向撓度最大值

不同矢跨比所對應的拱肋豎向變形如圖7、圖8、圖9所示，不同矢跨比所對應的拱肋豎向撓度最大值的變化圖如圖10所示。

圖71/6矢跨比對應的拱肋豎向位移圖

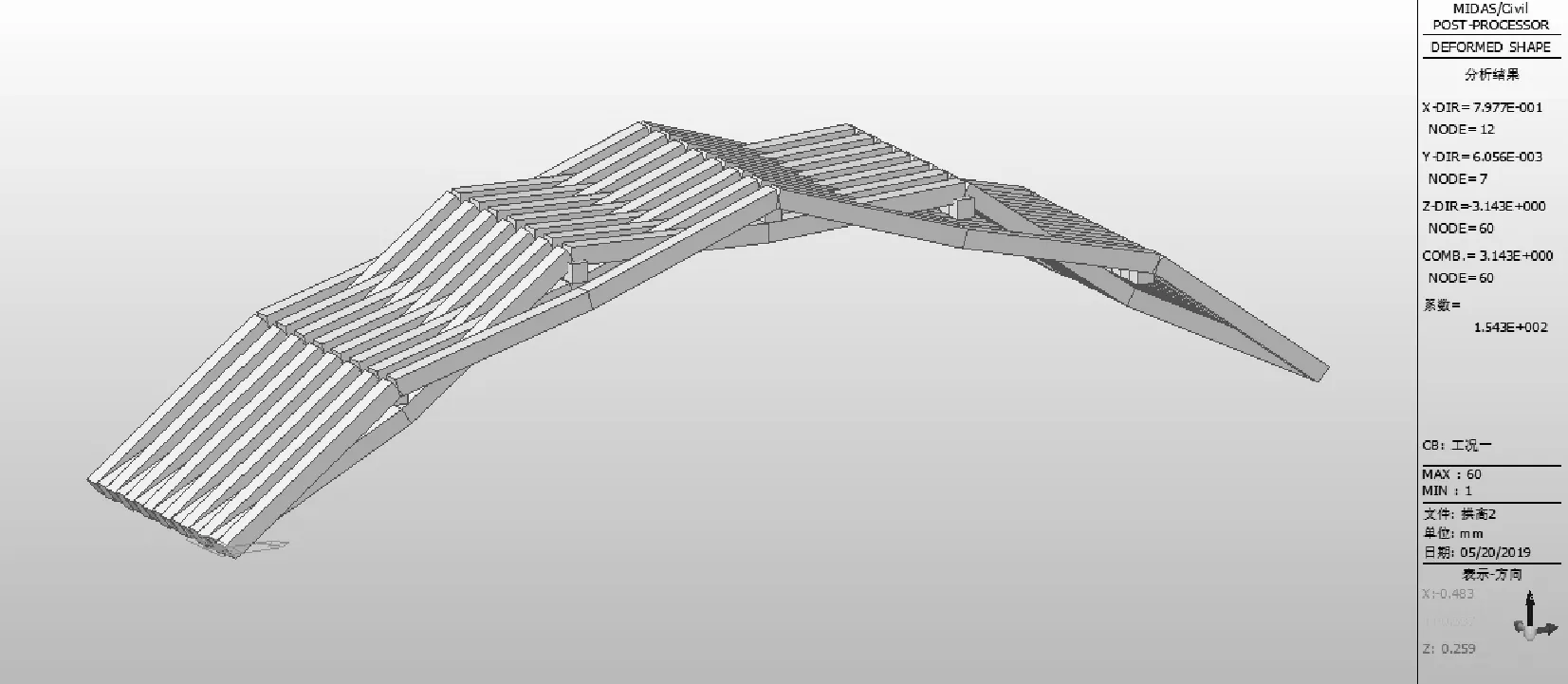
圖81/4矢跨比對應的拱肋豎向位移圖

圖91/3矢跨比對應的拱肋豎向位移圖

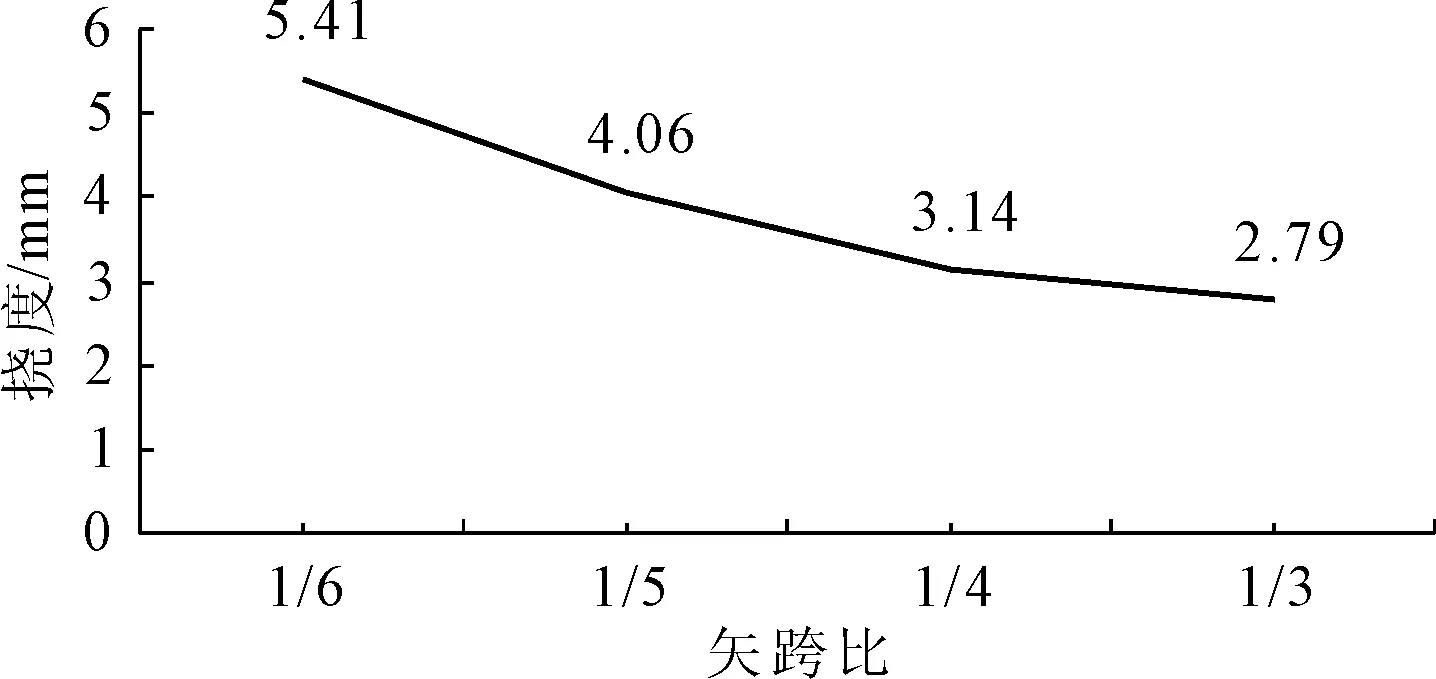
圖10不同矢跨比對應的拱肋豎向撓度變化圖

由上述計算結果比較，可以發現：隨著拱肋結構矢跨比的增大，構件內最大撓度值逐漸降低。

由上文可知，隨著矢跨比的增大，拱肋節點處的角度變小，拱肋內部所產生的最大壓應力也變小，因壓應力所產生的結構位移也隨著變小。

2.2.3 極限承載能力分析

根據《城市人行天橋與人行地道技術規范》[12](CJJ 69—1995)中有關人行橋剛度應滿足限制L/800=9 584 mm/800=11.98 mm的要求。拱肋結構達到極限承載能力狀態時，拱肋最大應力、最大撓度及施加總荷載見表7。

從計算結果可以看出：當拱肋結構達到極限承載能力，隨著拱肋結構矢跨比的增大，構件所能承受的總外荷載也不斷增大。

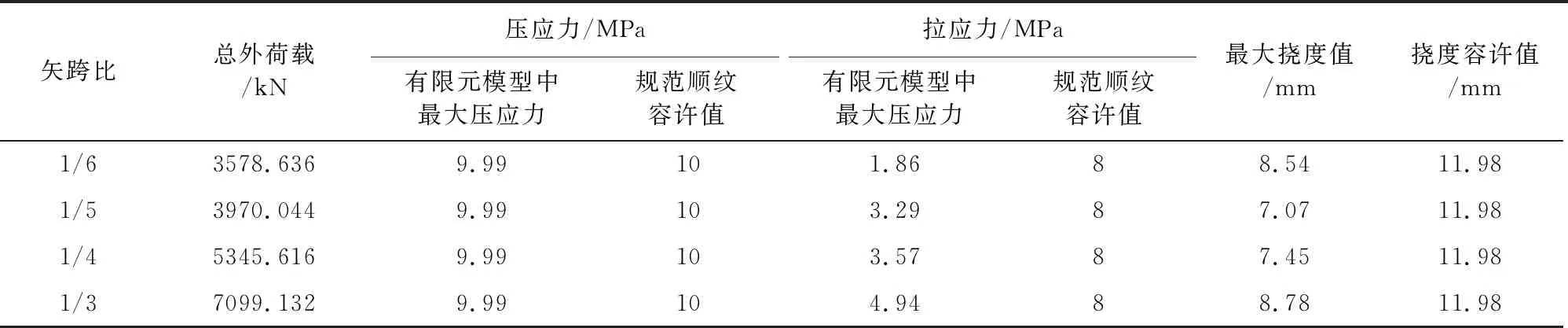
表7 極限承載能力狀態下拱肋最大應力、撓度及外荷載

綜合上述強度分析、撓度分析和極限承載能力分析可知：在承載能力極限組合作用下，隨著拱肋結構矢跨比的增大，拱肋節點處的角度隨之減小，拱肋最大應力值和最大撓度值均逐漸遞減；當拱肋結構達到極限承載能力時，隨著矢跨比的增大，拱肋結構所能承受的外荷載也隨之增大。查閱橋涵設計規范，針對拱橋構造，矢跨比不宜大于1/4，故我們采用1/4矢跨比作為最優矢跨比。

2.3 節間數分析

2.3.1 強度分析

在承載能力極限組合作用下，不同節間數所對應的拱肋最大應力值見表8。

不同矢跨比所對應的拱肋應力圖如圖11、圖12、圖13所示，不同矢跨比所對應的拱肋最大應力值的變化圖如圖14所示。

表8 不同節間數所對應的拱肋最大應力值

圖11 五節拱對應的拱肋應力圖

圖12七節拱對應的拱肋應力圖

圖13九節拱對應的拱肋應力圖

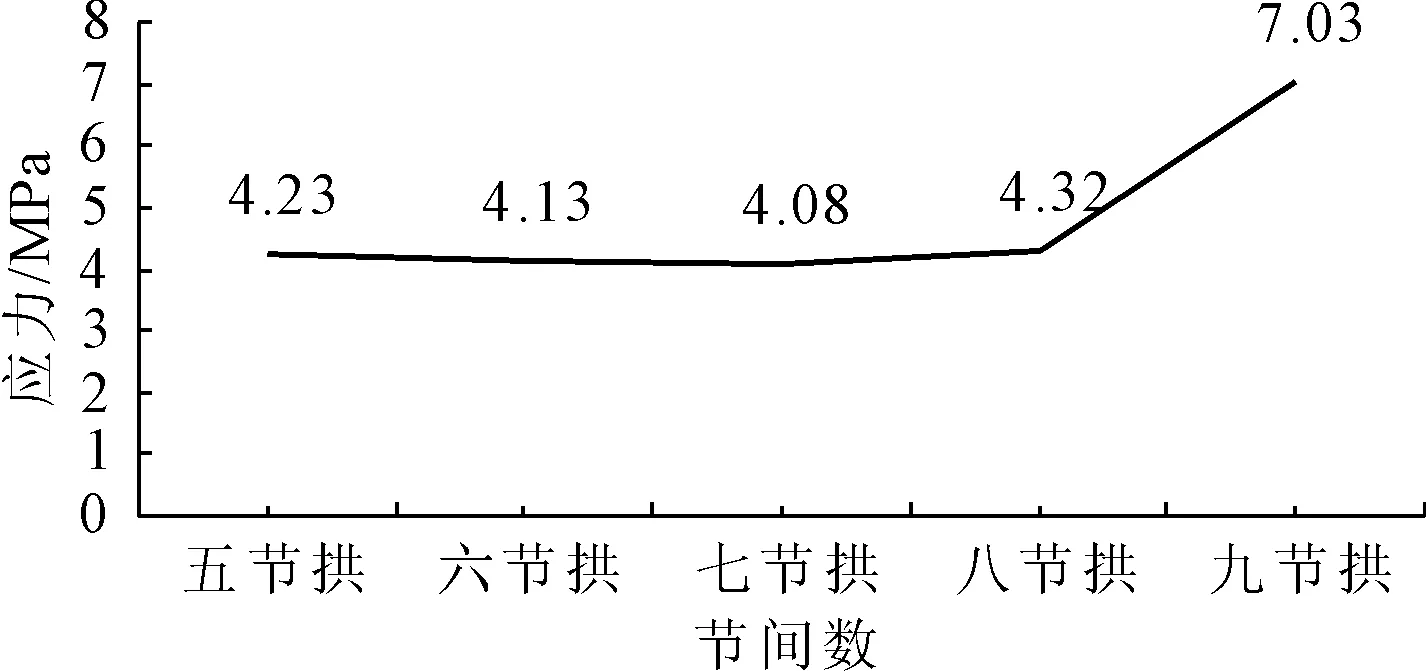
圖14不同節間數對應的拱肋結構最大應力變化圖

由上述計算結果，可以看出：隨著節間數的增加，拱肋結構內最大應力先減小然后突然增大。

(1) 由于節點對整體結構的強度存在削弱作用[13]，當結構為五節拱、六節拱或者七節拱時，結構節點數相對較少，節點數增加對于結構的削弱作用還不是很明顯，并且，節間數的增加使結構漸漸趨近于真正的圓拱，其受力形式也與真正的拱形越來越相似，拱肋內最大壓應力逐漸減小。

(2) 當結構為超過七節拱的拱形時，節點數相對較多，反而使得結構趨于復雜，且較多的節點對結構強度剛度有著明顯的削弱，又由于結構已經十分接近真正的圓拱形，通過增加節間數使結構獲得趨近于圓拱的受力形式已經不能抵消節點的消弱作用，反而會引起拱肋內最大壓應力增大，結構受力不合理。

2.3.2 撓度分析

在承載能力極限組合作用下，不同節間數所對應的拱肋豎向撓度最大值見表9，表中豎向位移數值以豎直向下為正。

不同節間數所對應的拱肋豎向變形如圖15、圖16、圖17所示，不同矢跨比所對應的拱肋豎向撓度最大值的變化圖如圖18所示。

表9 不同節間數所對應的拱肋豎向撓度最大值

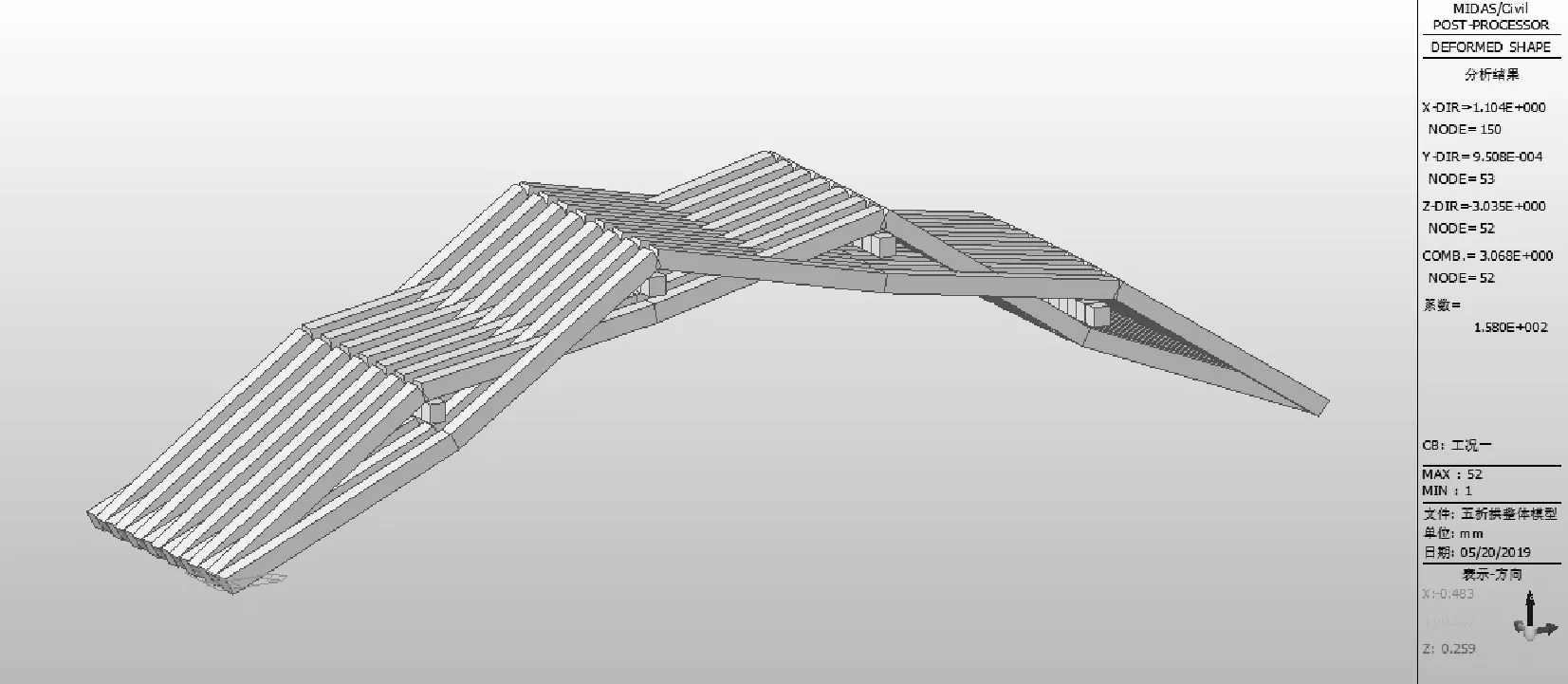
圖15五節拱對應的拱肋豎向位移圖

圖16七節拱對應的拱肋豎向位移圖

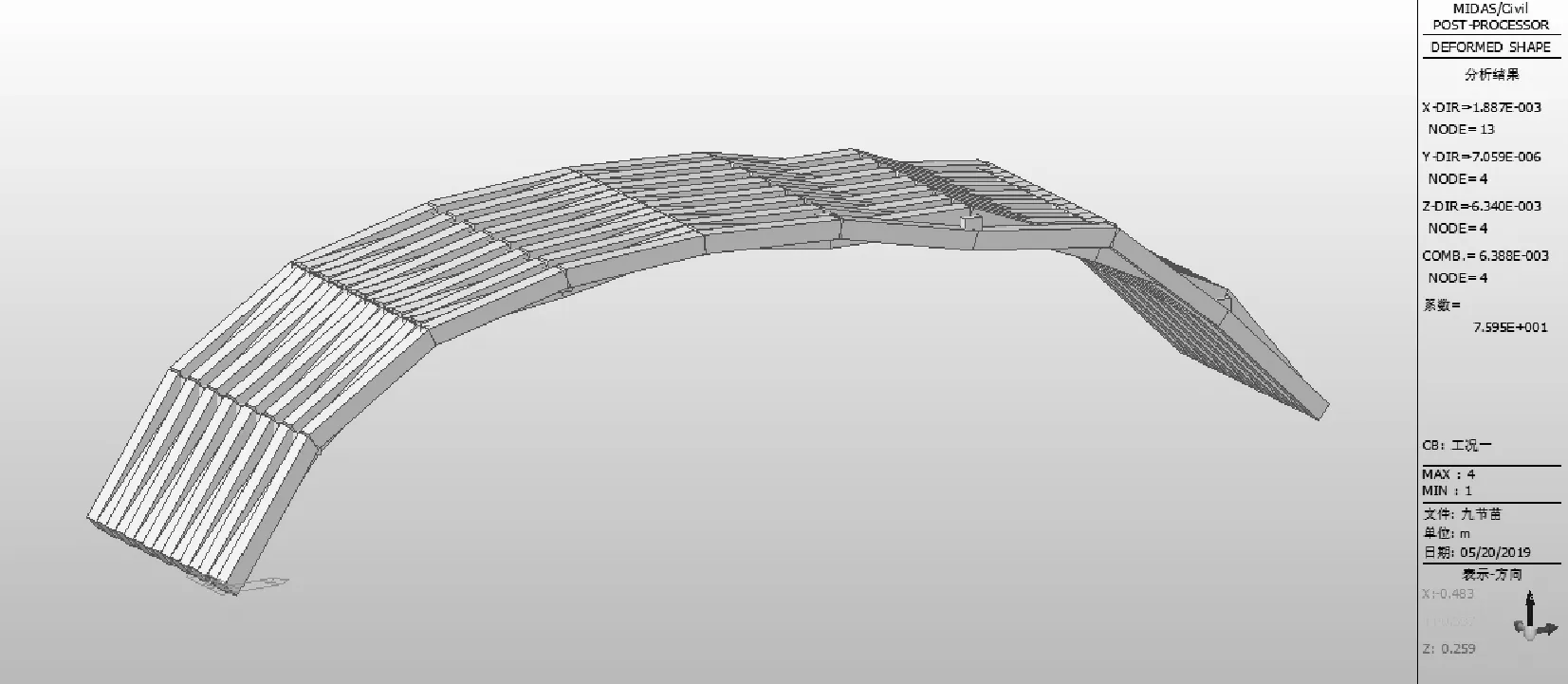
圖17九節拱對應的拱肋豎向位移圖

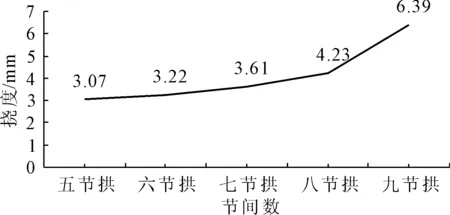
圖18不同節間數對應的拱肋豎向撓度變化圖

由上述計算結果，可以看出：隨著節間數的增加，拱肋結構的最大撓度值一直增大。

由于節點對整體結構的剛度存在削弱作用，隨著節間數的增加，結構節點也隨之增多，結構的整體剛度也逐漸降低，虹橋拱肋的最大撓度也隨之逐漸增大。當結構在五節拱至七節拱之間，撓度增加較為緩慢，彼此相差不大；當拱肋結構超過七節拱時，撓度增幅很大，可見結構的剛度會隨節間數的增加不斷減弱，也就是說，由于節點的增加，使得結構變“柔”[14]。

2.3.3 極限承載能力分析

當拱肋結構達到極限承載能力狀態時，拱肋最大應力、最大撓度及施加總荷載見表10。

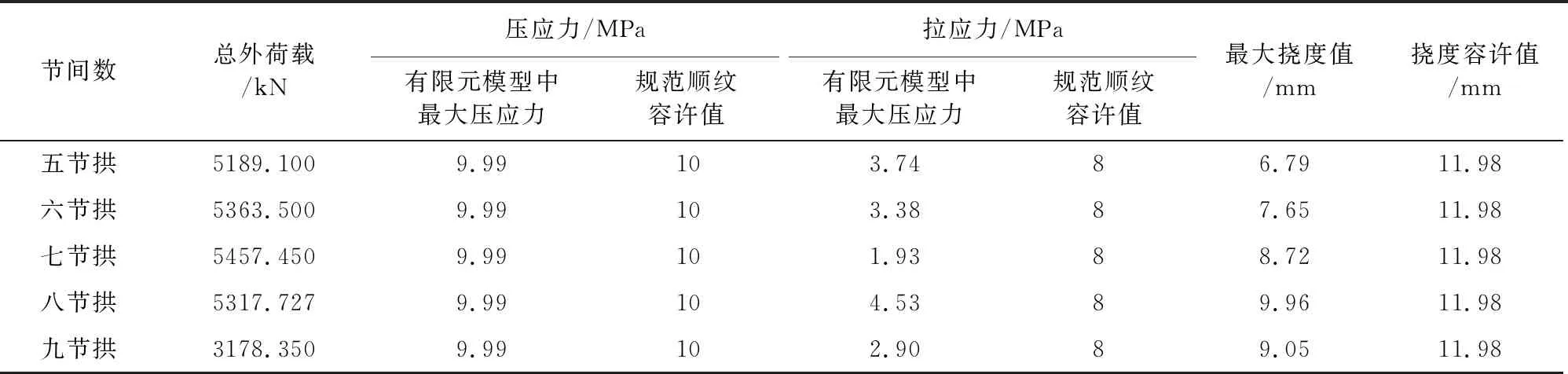
表10 極限承載能力狀態下拱肋最大應力、撓度及外荷載

從計算結果可以看出：當拱肋結構達到極限承載能力時，隨著拱肋結構節間數的增加，構件所能承受的總外荷載先增大后減小。

綜合上述強度分析、撓度分析和極限承載能力分析可知：在承載能力極限組合作用下，當結構為七節拱時，拱肋內的最大壓應力最小，而最大撓度與五節拱、六節拱的最大撓度相差較小；當拱肋結構達到極限承載能力時，拱肋為七節拱時，結構所能承受的外荷載最大，故七節拱是較優的結構形式。

2.4 拱肋截面分析

2.4.1 強度分析

在承載能力極限組合作用下，不同截面尺寸所對應的拱肋最大應力值見表11。

表11 不同節間數所對應的拱肋最大應力值

不同截面尺寸所對應的拱肋應力圖如圖19、圖20、圖21所示，不同截面尺寸所對應的拱肋最大應力值的變化圖如圖22所示。

圖19截面1對應的拱肋應力圖

由上述計算結果可以看出：隨著截面尺寸的增加，拱肋結構內最大應力逐漸減小。

由于拱肋自重遠小于節點處施加的外荷載，隨著截面尺寸的增大，結構剛度也隨之增大，拱肋自重增大對結構的影響遠小于拱肋剛度增大對結構的影響[15]。因而在合理的截面尺寸范圍內，隨著拱肋截面尺寸的增大，拱肋結構越有利于受力。

圖20截面3對應的拱肋應力圖

圖21截面4對應的拱肋應力圖

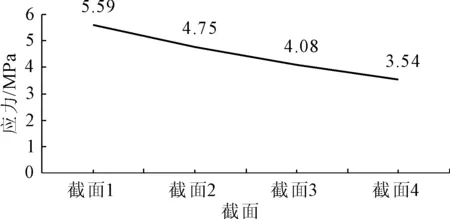
圖22不同截面尺寸對應的拱肋結構最大應力變化圖

2.4.2 撓度分析

在承載能力極限組合作用下，不同截面尺寸所對應的拱肋豎向撓度最大值見表12，表中豎向位移數值以豎直向下為正。

不同截面尺寸所對應的拱肋豎向變形如圖23、圖24、圖25所示，不同截面尺寸所對應的拱肋豎向撓度最大值的變化圖如圖26所示。

表12 不同節間數所對應的拱肋豎向撓度最大值

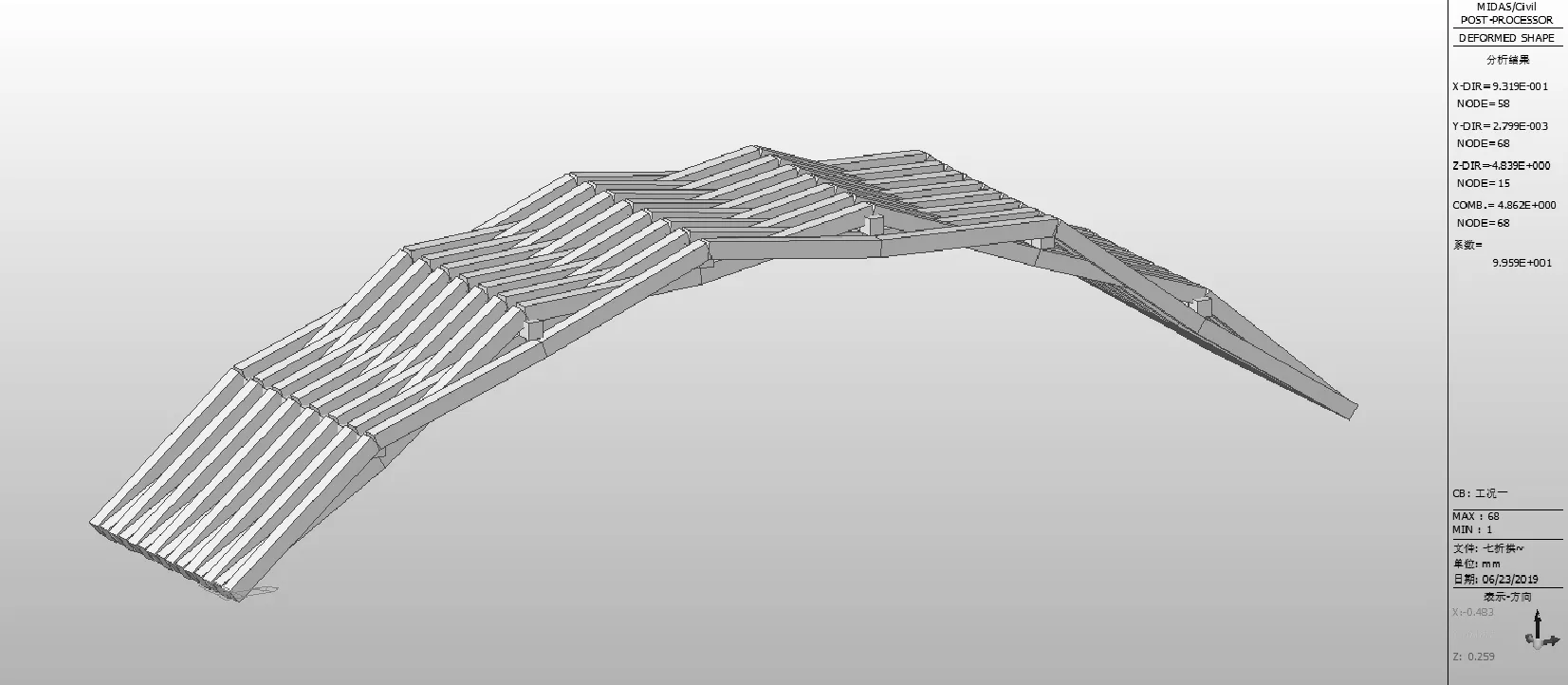
圖23截面1對應的拱肋豎向位移圖

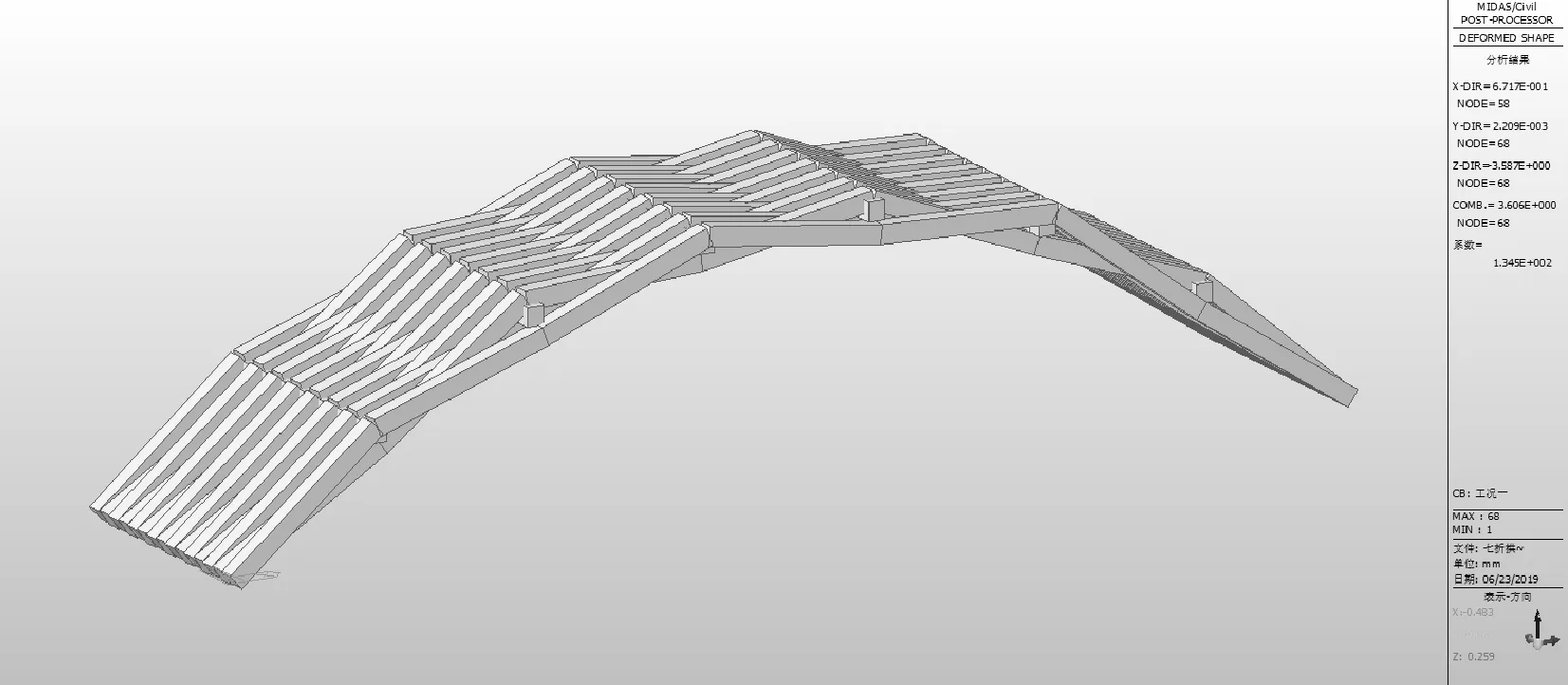
圖24截面3對應的拱肋豎向位移圖

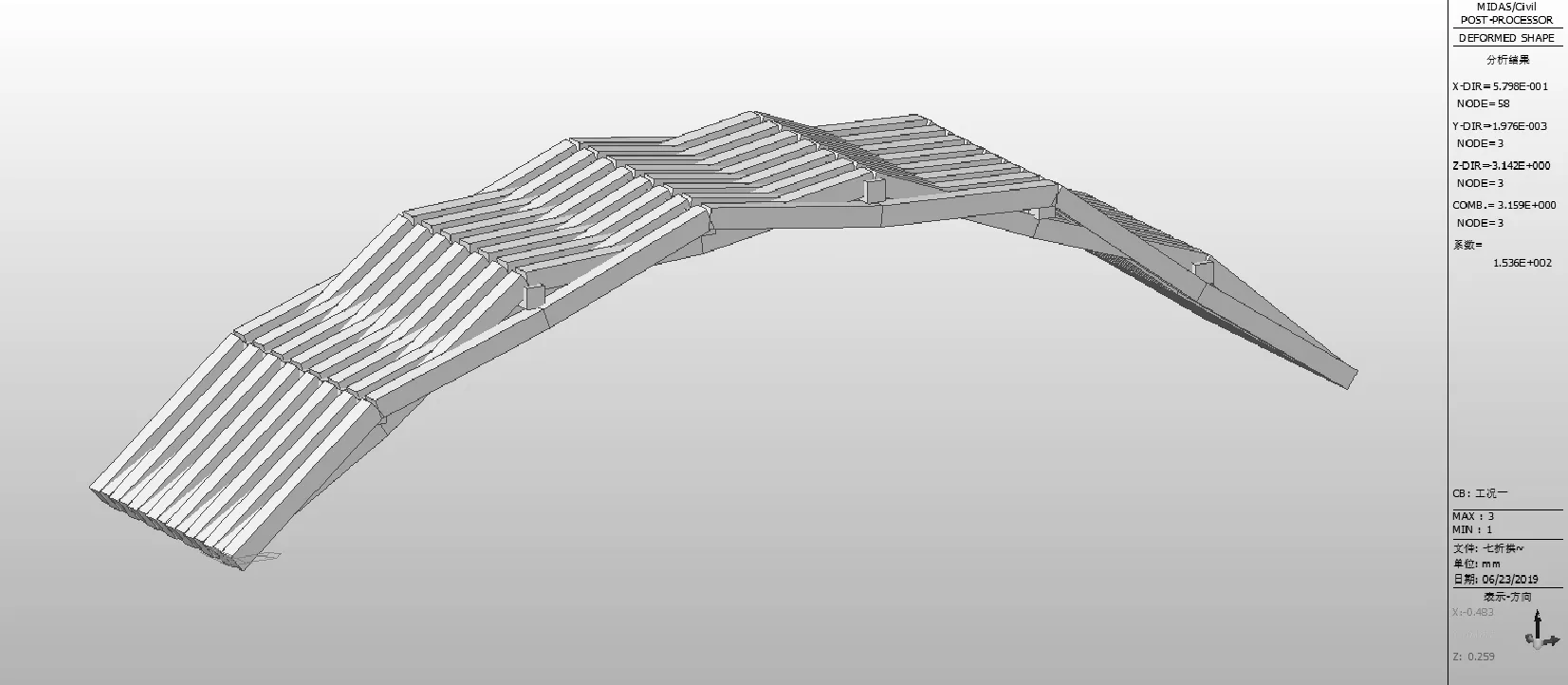
圖25截面4對應的拱肋豎向位移圖

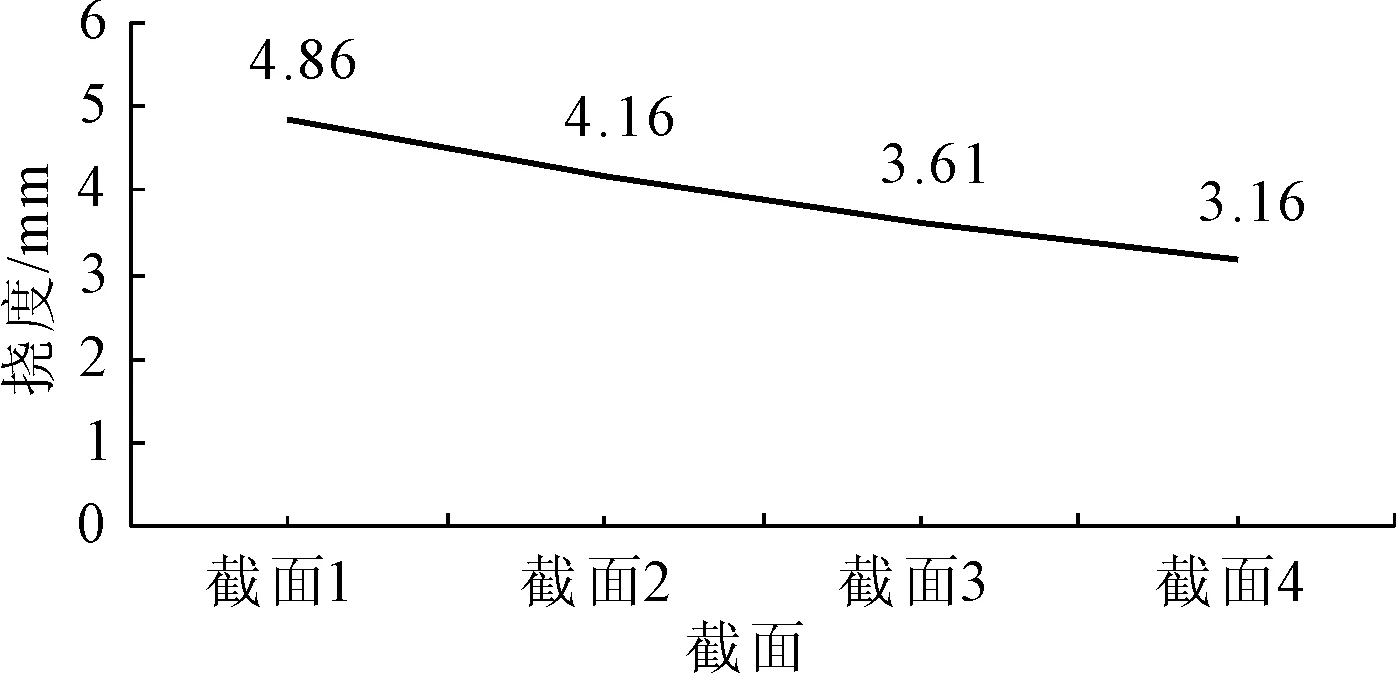
圖26不同截面尺寸對應的拱肋豎向撓度變化圖

由上述計算結果可以看出：隨著截面尺寸的增加，拱肋結構的最大撓度隨之減小。

由于拱肋自重遠小于節點處施加的外荷載，隨著截面尺寸的增大，結構剛度也隨之增大，拱肋結構的最大豎向撓度也隨之減小。

2.4.3 極限承載能力分析

當拱肋結構達到極限承載能力狀態時，拱肋最大應力、最大撓度及施加總荷載見表13。

從計算結果可以看出：當拱肋結構達到極限承載能力時，隨著拱肋結構截面尺寸的增加，構件剛度隨之增大，結構所能承受的總外荷載也隨之增大。

綜合上述強度分析、撓度分析和極限承載能力分析可知：在承載能力極限組合作用下，隨著拱肋截面尺寸的增大，拱肋最大應力和最大撓度逐漸減小；當拱肋結構達到極限承載能力時，隨著拱肋截面尺寸的增大，拱肋所能承受的最大荷載隨之增大。

3 結 論

(1) 通過上述分析可知：拱肋結構的矢跨比主要通過影響構件節點處的幾何關系來影響結構的承載能力；而拱肋結構的節間數和拱肋截面尺寸主要通過影響構件的剛度來影響結構的承載能力的。

(2) 在承載能力極限組合作用下，隨著矢跨比的增加，拱肋結構內的最大應力和最大撓度均隨之減少：隨著節間數的增加，拱肋內應力也逐漸減少，但當結構拱形超過七節拱時，隨著節間數的增加，節點也隨之增多，趨近于圓拱的受力形式已經不足以抵消大量節點帶來對的結構的削弱作用了，使得拱肋內應力不減反增；隨著拱肋截面的增大，拱肋結構內的最大應力和最大撓度均隨之減少。

(3) 當拱肋結構達到極限承載能力時，隨著矢跨比的增大，拱肋結構所能承受的外荷載也隨之增大；隨著拱肋結構節間數的增加，構件所能承受的總外荷載先增大后減小；隨著拱肋截面尺寸的增大，拱肋所能承受的最大荷載隨之增大。

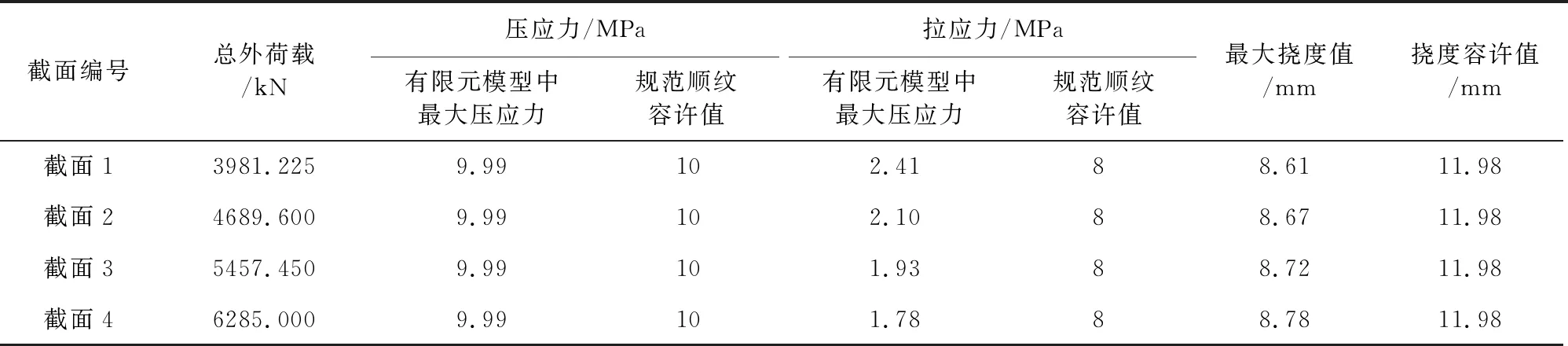
表13 極限承載能力狀態下拱肋最大應力、撓度及外荷載

(4) 通過對改變拱肋結構矢跨比、節間數和拱肋截面尺寸的分析比較中發現，在設計類似木拱橋時，要根據現場實際情況充分考慮上述三個因素對編木拱結構的影響，以得到一個最為合理的矢跨比、節間數和拱肋截面尺寸。