從教材出發以能力立意

錢德春

圖形與幾何是初中數學的重要內容，因其直觀性、邏輯性、演繹性和系統性等特點，一直為廣大初中數學教師所重視，也受到中考數學命題者的青睞。幾何壓軸題既要基于學生認知，體現課標要求，尊重教學現實，又要有所創新，這對命題者來說具有一定的挑戰性。事實上，數學教材提供了豐富的命題素材。充分挖掘素材的命題價值，考查學生的能力，是一種正確的命題導向。本文基于對2019年泰州卷第25題的特點分析，談談幾何與圖形試題命制與教學思考。

一、真題呈現

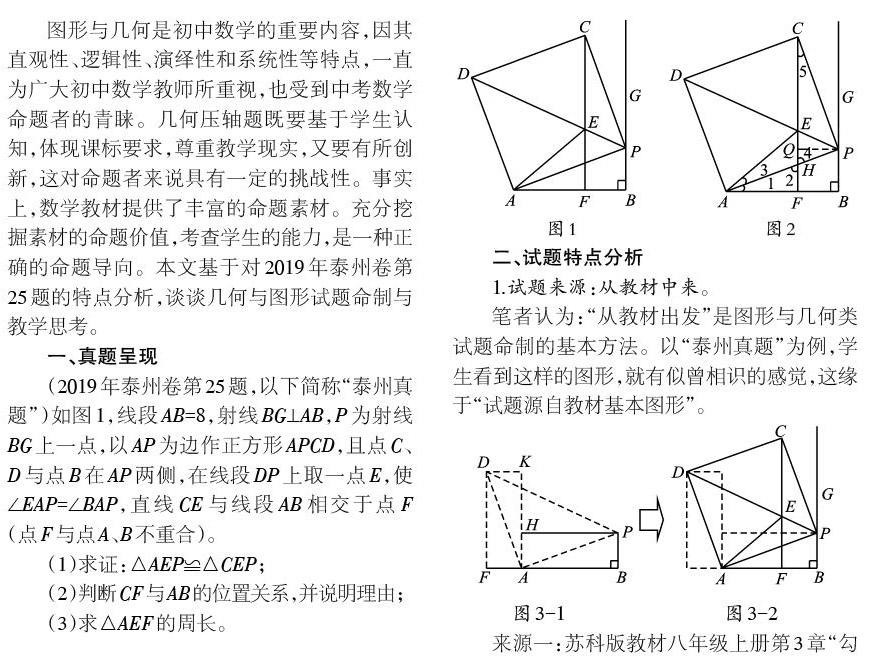
（2019年泰州卷第25題，以下簡稱“泰州真題”）如圖1，線段AB=8，射線BG⊥AB，P為射線BG上一點，以AP為邊作正方形APCD，且點C、D與點B在AP兩側，在線段DP上取一點E，使∠EAP=∠BAP，直線CE與線段AB相交于點F（點F與點A、B不重合）。

（1）求證：△AEP≌△CEP;

（2）判斷CF與AB的位置關系，并說明理由;

（3）求△AEF的周長。

二、試題特點分析

1.試題來源：從教材中來。

筆者認為：“從教材出發”是圖形與幾何類試題命制的基本方法。以“泰州真題”為例，學生看到這樣的圖形，就有似曾相識的感覺，這緣于“試題源自教材基本圖形”。

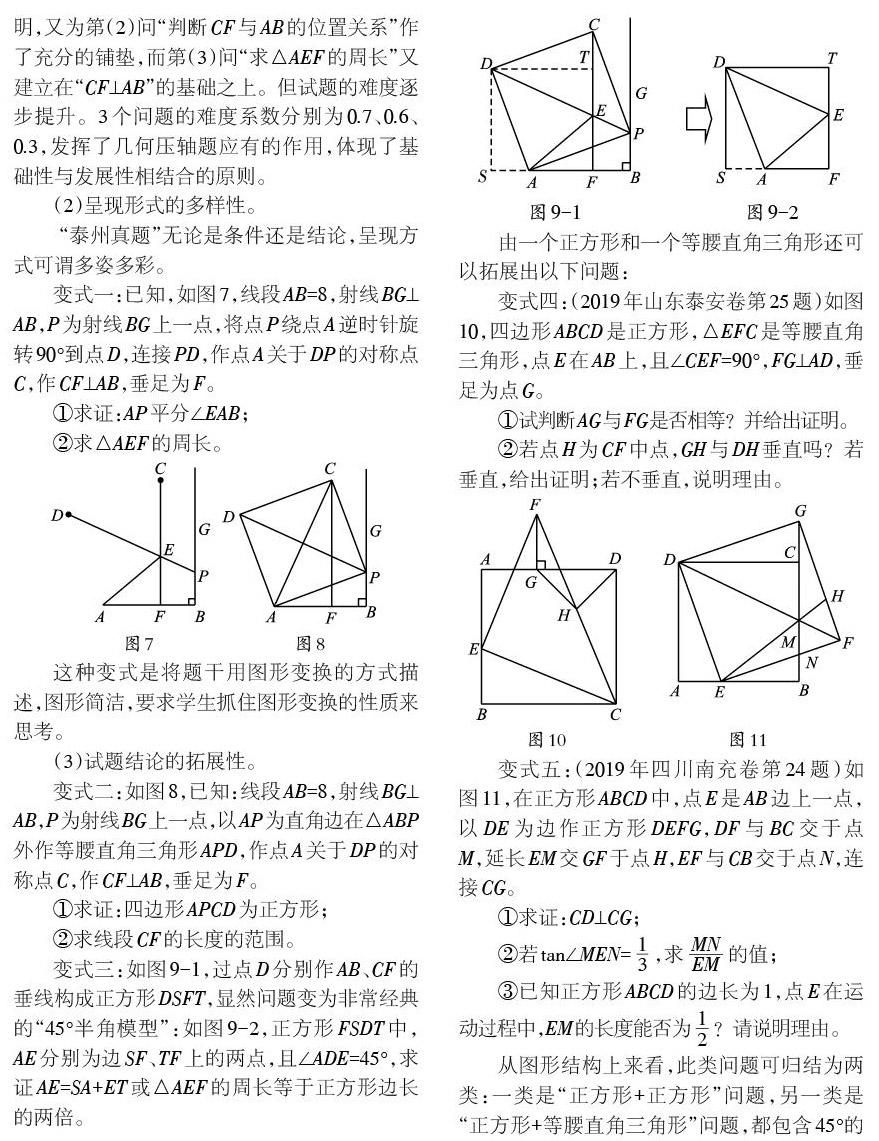
來源一：蘇科版教材八年級上冊第3章“勾股定理”第81頁的探索。

把一個直立的火柴盒AKDF放倒（如圖3-1），你能用不同的方法計算梯形DFBP的面積，驗證勾股定理嗎？

圖中隱含了等腰直角△ADP，將該三角形沿PD翻折至△CDP位置，過點C作AB的垂線（如圖3-2），便得到試題圖形。

來源二：蘇科版教材八年級下冊第9章“中心對稱圖形——平行四邊形”第82頁例題。

如圖4-1，在正方形BTKF中，點P、C、D、A分別在BT、TK、KF、FB上，且BP=TC=KD=FA，求證：四邊形PCDA是正方形。

隱去圖4-1中的線段FA、FD、DK、KC、CT，并過點C作AB的垂線，便得到試題圖形（圖4-2）。

這種命題方式關注了學生的應試心理，引導教師教學要從教材出發，充分挖掘并發揮教材的教學價值。

2.試題探究：從“兩頭”出發。

“泰州真題”的難點在第（3）問，但探究與分析是常用的策略——“從兩頭向中間”，即“從條件出發”向結論“挺進”，“從結論出發”向條件“靠攏”。這需要一定的聯想能力，也需要較強的模型意識。

（1）從條件出發。

分析題干、圖1及第（1）（2）小問中的結論發現下列條件：①線段AB=8;②四邊形APCD是正方形;③△ABP是直角三角形;④△AEP≌△CEP;⑤CF與AB垂直。這些條件可以得出角的關系、線段相等，為解決問題提供了保障。

（2）從結論出發。

△AEF的周長=AF+EF+AE。所求的未知量一定與線段AB=8有關系，這就需要線段轉換。如何轉換？結合條件“AE=CE”，有△AEF的周長=AF+CF，故考慮AF+CF與AB的關系，繼續進行線段轉換。利用圖形中“AP=CP”的條件，可通過構造三角形全等轉換線段。

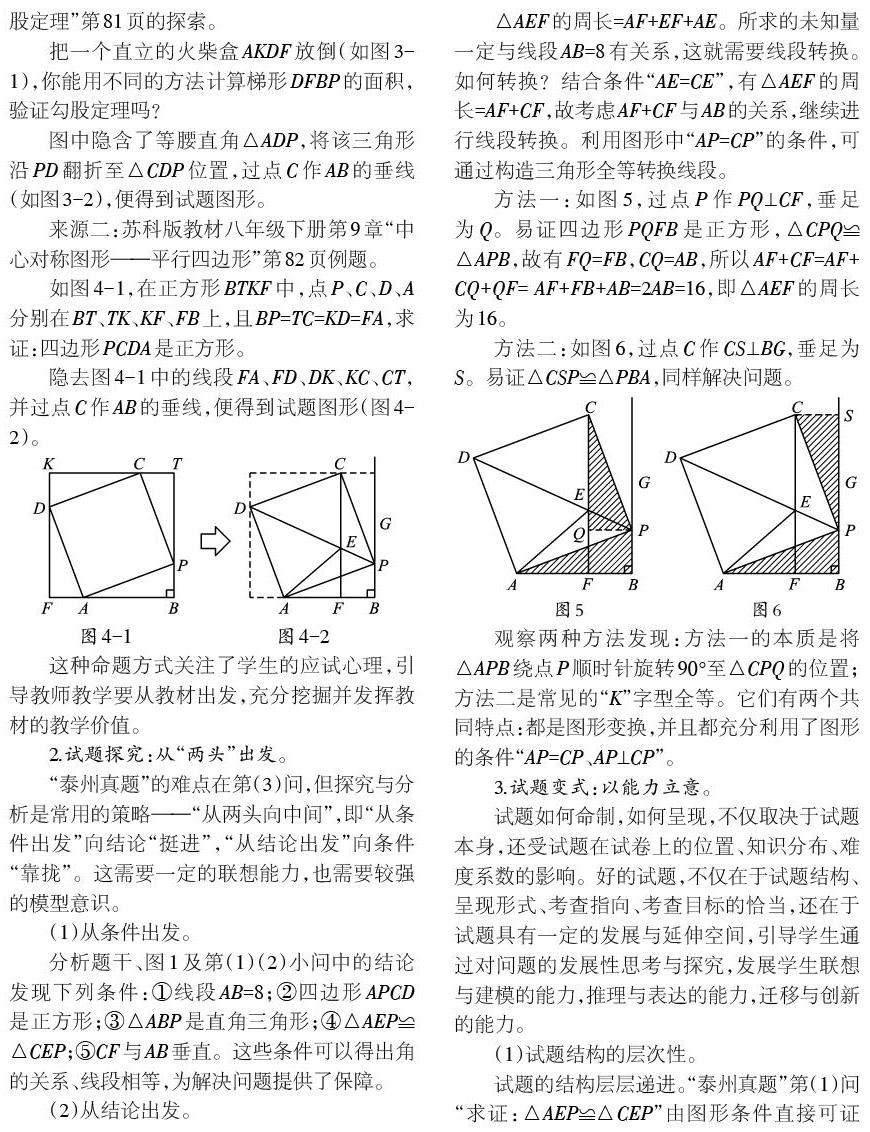
方法一：如圖5，過點P作PQ⊥CF，垂足為Q。易證四邊形PQFB是正方形，△CPQ≌△APB，故有FQ=FB，CQ=AB，所以AF+CF=AF+CQ+QF= AF+FB+AB=2AB=16，即△AEF的周長為16。

方法二：如圖6，過點C作CS⊥BG，垂足為S。易證△CSP≌△PBA，同樣解決問題。

觀察兩種方法發現：方法一的本質是將△APB繞點P順時針旋轉90°至△CPQ的位置;方法二是常見的“K”字型全等。它們有兩個共同特點：都是圖形變換，并且都充分利用了圖形的條件“AP=CP、AP⊥CP”。

3.試題變式：以能力立意。

試題如何命制，如何呈現，不僅取決于試題本身，還受試題在試卷上的位置、知識分布、難度系數的影響。好的試題，不僅在于試題結構、呈現形式、考查指向、考查目標的恰當，還在于試題具有一定的發展與延伸空間，引導學生通過對問題的發展性思考與探究，發展學生聯想與建模的能力，推理與表達的能力，遷移與創新的能力。

（1）試題結構的層次性。

試題的結構層層遞進。“泰州真題”第（1）問“求證：△AEP≌△CEP”由圖形條件直接可證明，又為第（2）問“判斷CF與AB的位置關系”作了充分的鋪墊，而第（3）問“求△AEF的周長”又建立在“CF⊥AB”的基礎之上。但試題的難度逐步提升。3個問題的難度系數分別為0.7、0.6、0.3，發揮了幾何壓軸題應有的作用，體現了基礎性與發展性相結合的原則。

（2）呈現形式的多樣性。

“泰州真題”無論是條件還是結論，呈現方式可謂多姿多彩。

變式一：已知，如圖7，線段AB=8，射線BG⊥AB，P為射線BG上一點，將點P繞點A逆時針旋轉90°到點D，連接PD，作點A關于DP的對稱點C，作CF⊥AB，垂足為F。

①求證：AP平分∠EAB;

②求△AEF的周長。

這種變式是將題干用圖形變換的方式描述，圖形簡潔，要求學生抓住圖形變換的性質來思考。

（3）試題結論的拓展性。

變式二：如圖8，已知：線段AB=8，射線BG⊥AB，P為射線BG上一點，以AP為直角邊在△ABP外作等腰直角三角形APD，作點A關于DP的對稱點C，作CF⊥AB，垂足為F。

①求證：四邊形APCD為正方形;

②求線段CF的長度的范圍。

變式三：如圖9-1，過點D分別作AB、CF的垂線構成正方形DSFT，顯然問題變為非常經典的“45°半角模型”：如圖9-2，正方形FSDT中，AE分別為邊SF、TF上的兩點，且∠ADE=45°，求證AE=SA+ET或△AEF的周長等于正方形邊長的兩倍。

由一個正方形和一個等腰直角三角形還可以拓展出以下問題：

變式四：（2019年山東泰安卷第25題）如圖10，四邊形ABCD是正方形，△EFC是等腰直角三角形，點E在AB上，且∠CEF=90°，FG⊥AD，垂足為點G。

①試判斷AG與FG是否相等？并給出證明。

②若點H為CF中點，GH與DH垂直嗎？若垂直，給出證明;若不垂直，說明理由。

變式五：（2019年四川南充卷第24題）如圖11，在正方形ABCD中，點E是AB邊上一點，以DE為邊作正方形DEFG，DF與BC交于點M，延長EM交GF于點H，EF與CB交于點N，連接CG。

①求證：CD⊥CG;

②若tan∠MEN=[13]，求[MNEM]的值;

③已知正方形ABCD的邊長為1，點E在運動過程中，EM的長度能否為[12]？請說明理由。

從圖形結構上來看，此類問題可歸結為兩類：一類是“正方形+正方形”問題，另一類是“正方形+等腰直角三角形”問題，都包含45°的角;從解題方法上看，都利用三角形旋轉型全等的方法;從試題發展上看，此類問題可向三角形相似、解直角三角形、代數方程、函數等方向發展，試題的發展性給教師教學與學生學習提供了廣闊的空間。

（4）數學思想的滲透性。

感悟蘊含在數學問題之中的數學思想方法既是一種數學能力，更是一種數學素養。試卷滲透了初中數學的主要思想方法，以此體現對學生數學素養的考查。如“泰州真題”第（1）問中的證明△AEP、△CEP關于PD軸對稱，體現了對稱變換的思想;問題中全等的三角形△APB與△CPQ，其中的△CPQ可以看成由△APB繞著點P順時針旋轉90°得到，體現了旋轉變換的思想;問題中點P在運動，但△AEF的周長始終等于2AB，體現了變中不變的思想。

三、教學啟示

1.課標、教材是數學教學的源頭。

在數學教學中有兩類現象：一是教學內容超標，恣意拔高教學要求;二是拋開教材“肆意發揮”。筆者在一所學校發現：有二十幾位數學教師的九年級備課組，居然找不到一本數學教材，這些現象必須引起高度重視。課程標準是教學的根本大法，也是教學評價的基本依據;教材將課程標準具體化，是教師的教材，也是學生的學材。教材中的公式、定理本質上就是數學模型，其結構與方法具有典型性、獨創性，其結論具有廣泛的應用性。因此，教學中要充分發揮教材的作用。

一是從教材出發。要體會教材編寫意圖和指向意義，充分挖掘與拓展教材，對教學資源進行二度開發，實現其應有的教學價值。如將圖3-1、4-1適當補形或添加條件，就變成了思維含量較高的幾何問題。

二是回到教材中。對于外來試題，從教材中找到源頭，用教材中的知識、方法與原理給予解釋。如圖10、圖11看似比較復雜，但將圖形與問題適當分解或轉換，便可還原為教材中的基本圖形、基本問題。

2.學生發展是數學教學的宗旨。

數學教學旨在促進學生數學知識內化、數學能力提高，數學素養提升，但最根本的目標是促進學生終身發展，而學生終身發展所必備的數學能力包括探究與思維能力、聯系與整合能力、推理與表達能力以及遷移與創新能力等。

（1）發展學生的探究與思維能力。

數學學習需要經歷操作、觀察、發現、猜想的過程，這個過程考驗的是學生的探究能力。發現與猜想的結論正確嗎？這就需要從定義、公理、定理出發，通過推理來證實或者證偽。這個過程更需要思維的參與。思維的方式較多，如形象思維與抽象思維、發散性思維與收斂性思維、批判性思維與反思性思維。

以“泰州真題”第（3）問為例，結論中的“△AEF周長”，必然與條件中的“線段AB=8”關聯。那么二者間有何聯系呢？這就需要操作、觀察與猜想。如通過測量，直觀地發現△AEF周長為AB長的兩倍。這個猜想正確嗎？此時需要深度思維。由△AEP≌△CEP可將△AEF周長轉化為AF+CF，而要出現2AB，由條件AP=CP繼續通過構造三角形全等轉化。

探究與思維能力的培養要貫穿數學教學的全過程。如定理、公式的教學，不能只是關注結論的應用，而要引導學生經歷“再創造”過程，通過操作、觀察，發現、猜想結論，通過推理證明結論，或推翻結論。

（2）增強學生的聯系與整合能力。

數學問題應該如何思考與分析？筆者認為，可以從兩個方面進行。一是從條件出發：你想到了什么，還能想到什么，下一步又想到了什么。二是從結論出發：遇到這樣的結論有哪些策略，常用哪些方法。讓學生應盡可能多地說出想法、思路，不管這些思路對當前問題是否有效，教學中都應引導學生充分表達，只有這樣才能拓展思路。思路的拓展需要聯想，將條件、結論換一種表征方式就是一種聯想方法。如解決“求一點到直線的距離”問題中的關鍵詞是“距離”二字，就要抓住這個關鍵詞充分聯想。由“距離”聯想到“垂直”，進而聯想到“三角形的高”，再聯想到三角形的面積法;聯想“直角三角形”，考慮可否用“勾股定理”“直角三角形相似”“銳角三角函數”等。這里所有的思路都源自“距離”，將“距離”用不同的表征方式，便得到不同的解題思路，凸顯了聯想的神奇功效。

聯想的東西有時是分散的、零碎的。在“泰州真題”中，由條件及聯想可得“AB=8”“正方形APCD”“Rt△ABP”“△AEP≌△CEP”“CF⊥AB”等結論，這些結論哪些對解決問題有效，哪些無效，條件又如何用，都需要通過大腦的梳理、整合，使之結構化、序列化，為最終解決問題服務。

（3）強化學生的推理與表達能力。

“推理是數學的基本思維方式，也是人們學習和生活中經常使用的思維方式。”課程標準在談到數學思考時明確要求“能進行有條理的思考，能比較清楚地表達自己的思考過程與結果”。人類文明成果之所以能夠交流與流傳，得益于各種形式的表達與記載。因此，有序表達也是一種重要能力。面對數學問題，從尋找到解題思路到完整、準確寫出解題過程，這之間還有一段距離。從“泰州真題”的閱卷情況來看，學生推理與表達存在的問題較多。有的缺乏語言組織，如“泰州真題”解答需要用到“CQ=AB、QF=FB”，這些由“△CPQ≌△APB”和“正方形FBPQ”得到，有的學生只證明三角形全等，而不證明正方形就直接得到上述結論;有的邏輯混亂，如△AEP≌△CEP的證明用“SAS”，但不少學生將條件順序寫成“SSA”;有的敘述繁瑣，不能言簡意賅，如解題中涉及角的關系，標上數字就能一目了然，許多學生仍然用三個字母表示，讓人眼花繚亂;有的證明只是將定理堆砌在一起……如何解決這些問題，需要教師提出明確要求、適當板書示范，作業反饋矯正。

（4）增強學生遷移與創新能力。

創新能力是國家富強、民族興旺的不竭動力。“由此及彼”“由少及多”“由表及里”“由特殊及一般”的本質就是遷移，而創新的方式較多，如添加一個條件、弱化條件，把條件與結論交換，與其他問題結合;由量的變化到質的飛躍;對現象提出質疑，猜想結論并驗證結論，建構模型解決問題等都是創新。而數學中的抽象、建模和推理三大基本思想的本質就是創新。

如將“泰州真題”適當變化，則可以提出并探索新的問題。

一是將圖4-1的正方形改為正六邊形：如圖12，正六邊形ABCDEF的邊長為12，點A′、B′、C′、D′、E′、F′分別為邊AB、BC、CD、DE、EF、FA上的動點，且A′A=B′B=C′C=D′D=E′E=F′F。

①試證明線段A′D′一定經過某一定點;

②設A′B′C′D′E′F′的面積為S，求S的取值范圍。

二是將“泰州真題”條件一般化：如圖13，線段AB=a，∠ABG=α，P為射線BG上一點，以AP為邊作菱形APCD，使∠APC=α，且點C、D與點B在AP兩側，在線段DP上取一點E，使∠EAP=∠BAP，直線CE與線段AB相交于點F（點F與點A、B不重合）。

①若α=60°，請根據條件提出新的結論。（求證：△AEP≌△CEP;判斷CE與BG的位置關系，并說明理由;求點C運動路徑的長;④圖形中有長度不變的嗎？請說明理由。）

②若α為任意銳角呢？

教學中，教師要充分利用教材素材，拓展思維的廣度，挖掘思維的深度，發展學生的遷移與創新能力。

（作者單位：江蘇省泰州市教育局教研室）