船舶隨機(jī)參-強(qiáng)激勵橫搖概率密度函數(shù)的半解析方法研究?

劉利琴, 劉亞柳, 呂鑫鑫, 李 妍

(天津大學(xué)水利工程仿真與安全國家重點實驗室， 天津 300072)

船舶在遭遇惡劣海況時，為了避免遭受橫風(fēng)橫浪的影響，通常會調(diào)整航向，選擇縱浪或斜浪航行[1]。即使船舶在靜水中有足夠的穩(wěn)性，在縱浪和斜浪航行時仍有發(fā)生大角度搖擺乃至傾覆的可能。特別是當(dāng)船波遭遇頻率與船舶橫搖固有頻率比為 2時，很有可能發(fā)生參數(shù)橫搖甚至傾覆。參數(shù)橫搖發(fā)生的基本原理是船舶在航行過程中，由于波長近似等于船長，可認(rèn)為波峰分別經(jīng)過船首-船中-船尾整個過程是一個完整的參數(shù)激勵周期。當(dāng)波峰位于船首/尾(即波谷位于船中)時，船舶首尾處的水線面要比靜水中的水線面大，即此時的船舶橫搖復(fù)原力矩要比靜水時的偏大；而當(dāng)波峰位于船中時，船舶首尾處的水線面要比靜水中的水線面小，即此時的船舶橫搖復(fù)原力矩要比靜水時的偏小。隨著船-波相對位置的周期性變化，船舶橫搖復(fù)原力矩也呈現(xiàn)出周期性變化，從而引發(fā)顯著的參數(shù)橫搖運動。因此，有必要研究縱浪和斜浪中航行船舶的穩(wěn)性及運動狀態(tài)，分析船舶傾覆的機(jī)理，為避免船舶傾覆提供操船決策。

早在1863年，F(xiàn)roude[2]就觀察到在縱浪中航行的船舶受到波浪激勵會發(fā)生大幅橫搖的現(xiàn)象，只是當(dāng)時的知識還無法解釋該現(xiàn)象。隨著非線性理論的發(fā)展以及計算機(jī)技術(shù)的飛速發(fā)展，各國學(xué)者針對船舶參數(shù)橫搖運動進(jìn)行了大量的研究并取得了一些新的成果。Matusiak[3]對參數(shù)共振的理論進(jìn)行了研究。他提出了完整的六自由度數(shù)學(xué)模型。其研究表明：產(chǎn)生橫搖參數(shù)共振的最主要的原因是傅汝德-克雷洛夫力和復(fù)原力矩的非線性特性。Silva等[4-5]提出了基于切片理論研究迎浪船舶動穩(wěn)性的新方法，并將該方法拓展到船舶六自由度非線性運動模型，通過與試驗結(jié)果對比，驗證了該方法的可行性。Silva和Soares[6]采用橫搖-縱搖-垂蕩耦合的數(shù)學(xué)模型，進(jìn)行了數(shù)值模擬和運動穩(wěn)定性分析，并用模型試驗對研究結(jié)果加以驗證。研究發(fā)現(xiàn)：如果船舶遭受波浪的波長等于其船長、波浪的頻率為橫搖固有頻率的兩倍時，將有可能出現(xiàn)嚴(yán)重的橫搖參數(shù)共振現(xiàn)象，其橫搖角可達(dá)30°。Umeda[7]等考慮橫搖恢復(fù)力矩的變化研究了規(guī)則和隨機(jī)縱浪和斜浪中船舶的參數(shù)激勵橫搖運動，其橫搖恢復(fù)力矩系數(shù)的變化根據(jù)傾覆實驗求出。Vidic-Perunovic 等[8]采用一階可靠性方法計算船舶參數(shù)橫搖運動超過限定角度的概率。魯江、卜淑霞等[9]基于切片理論，提出了復(fù)原力的計算方法，計算過程中考慮了復(fù)原力中的輻射力和繞射力成分，并通過模型試驗驗證了數(shù)值計算方法的有效性。Dostal[10]針對隨機(jī)海況，應(yīng)用能量包線隨機(jī)平均法，理論推導(dǎo)了船舶參數(shù)橫搖響應(yīng)的概率密度函數(shù)。彭東升等[11]針對C11集裝箱船，計算了不同阻尼下船舶參數(shù)橫搖響應(yīng)。傅超等[12]對C11集裝箱船進(jìn)行了參數(shù)敏感性分析，提出通過改進(jìn)船舶設(shè)計減少參數(shù)橫搖發(fā)生的概率。Wei Chai[13]于2016年提出了一種能有效計算蒙特卡羅模擬的方法，并驗證該方法適用于統(tǒng)計船舶在隨機(jī)長峰波激勵下的參數(shù)橫搖響應(yīng)極值。

本文在前人工作的基礎(chǔ)上研究隨機(jī)斜浪中船舶參-強(qiáng)激勵橫搖響應(yīng)的概率密度函數(shù)。為實現(xiàn)解析求解，將數(shù)值模擬得到的復(fù)原力臂函數(shù)用近似的解析函數(shù)表示，將隨機(jī)海浪譜處理為窄帶隨機(jī)過程以得到隨機(jī)參數(shù)激勵和隨機(jī)強(qiáng)迫激勵的譜密度函數(shù)，采用能量包線隨機(jī)平均法計算系統(tǒng)響應(yīng)的穩(wěn)定概率密度函數(shù)。

1 船舶參數(shù)激勵橫搖運動方程

考慮隨機(jī)斜浪，假設(shè)船舶的垂蕩及縱搖運動為小量，船舶橫搖運動方程如下：

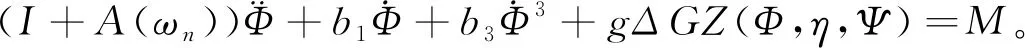
(1)

其中：Φ為橫搖角；I為橫搖慣性矩；A(ωn)為橫搖附加慣性矩；b1與b3分別為線性阻尼系數(shù)與立方非線性阻尼系數(shù)；Δ為排水量；g為重力加速度；M為波浪強(qiáng)迫激勵力矩；GZ(Φ,η,Ψ)為船舶復(fù)原力臂，由Φ、η和Ψ決定，其中η為長峰波的波動幅度，Ψ為船和波的相對位置，取值范圍為[0，2π]。

船舶在長峰波中的復(fù)原力臂GZ(Φ,η,Ψ)可基于切片理論求解，一般采用數(shù)值的方法進(jìn)行模擬[9]。

為了能夠使用隨機(jī)平均理論求解運動方程(1)，將GZ(Φ,η,Ψ)展開為如下的關(guān)于橫搖角Φ的多項式[14]：

GZa(Φ,η,Ψ)=q1Φ+q2Φ3+q3ηcΦ。

(2)

式中，ηc=ηcos(Ψ)，是由隨機(jī)波浪確定的隨機(jī)過程，可通過窄帶海浪譜展開得到；qi(i=1,2,3)為展開項的系數(shù)，使用最小二乘法確定，即使下式取得最小：

(3)

2 窄帶隨機(jī)海浪的數(shù)學(xué)描述

對于隨機(jī)海浪，一般用諧波疊加法來模擬不規(guī)則長峰波波面函數(shù)。為采用隨機(jī)平均法研究船舶隨機(jī)參-強(qiáng)激勵橫搖運動，以下將隨機(jī)波面升高處理為窄帶隨機(jī)過程Ze(x,t)，其表達(dá)式如下[10]：

Ze(x,t)=η1(t)cos(2πx/L)-η2(t)sin(2πx/L)。

(4)

其中，η1(t)和η2(t)均為高斯平穩(wěn)隨機(jī)過程，兩者互不相關(guān)、統(tǒng)計獨立[15-16]，表達(dá)式如下：

(5)

(6)

式中：ω為海浪頻率；S(ω)為海浪譜；ζ(ω)為隨機(jī)相位角。r=(L/2)k，其中L為特征波長，k為波數(shù)。

η1(t)和η2(t)對應(yīng)的譜密度函數(shù)分別為：

(7)

(8)

如果船舶以航向角β、航速U航行，則式(4)～(8)中的海浪頻率ω和海浪譜S(ω)要用對應(yīng)的遭遇頻率ωe和遭遇譜S(ωe)來替換，其表達(dá)式為：

ωe=ω-kUcosβ；

(9)

(10)

進(jìn)一步將隨機(jī)過程η2用受控自回歸滑動平均模型(CARMA(2,1))來模擬。對于CARMA(2,1)過程，需要滿足如下形式的微分方程：

(11)

(12)

(13)

其中，s=iω。采用最小二乘法，使式(13)與式(8)的誤差最小，從而確定ci(i=1,2,3)。

3 船舶隨機(jī)參-強(qiáng)激勵橫搖概率密度函數(shù)

采用能量包線隨機(jī)平均法研究船舶隨機(jī)參-強(qiáng)激勵橫搖運動概率密度函數(shù)。將船舶運動過程處理為馬爾可夫過程，將響應(yīng)量分成快變量與慢變量，通過對快變量的平均得到慢變量的近似方程，從而使系統(tǒng)的自由度縮減。

(14)

(15)

將響應(yīng)分量進(jìn)一步寫為快變量和慢變量，即系統(tǒng)由狀態(tài)空間(u,v)變換為狀態(tài)空間(u,H)，其中H為系統(tǒng)總能量，其表達(dá)式為：

(16)

式中，每個能量值H(u,v)對應(yīng)于特定的橫搖運動。對于確定的α1、α3值，可得到對應(yīng)于式(16)的能量等值線，用b(H)表示在特定能量值H下，系統(tǒng)所能達(dá)到的最大橫搖角，以下用b(H)來度量船舶的橫搖運動。

定義船舶橫搖的穩(wěn)性消失角如下：

(17)

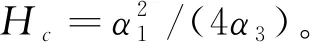
使用如下的轉(zhuǎn)換關(guān)系：

(18)

則運動方程(15)進(jìn)一步寫為：

(19)

引入中間變量Q(u,H)=v2，有：

(20)

則式(19)可進(jìn)一步寫為如下的隨機(jī)微分方程式：

(21)

根據(jù)隨機(jī)平均法，針對0≤H≤Hc，寫出上式的漂移與擴(kuò)散系數(shù)分別為[17]：

d(qt)}dτ。

(22)

(23)

其中，T(H)為時間區(qū)間，其表達(dá)式為：

(24)

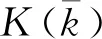
(25)

(26)

(27)

sn、cn、dn為雅克比橢圓函數(shù)，且有如下定義：

(28)

(29)

(30)

(31)

(32)

(33)

系統(tǒng)的能量H滿足如下的伊藤隨機(jī)微分方程：

dH=m(H)dt+σ(H)dWt。

(34)

對于上述伊藤隨機(jī)微分方程，其響應(yīng)為擴(kuò)散過程，對應(yīng)的轉(zhuǎn)移概率密度p(H,t|H0,t0)滿足如下的FPK方程：

(35)

上式中，(H0,t0)表示初始狀態(tài)。

式(35)可進(jìn)一步寫成如下的算子形式：

(36)

其中，L*為橢圓算子的伴隨算子，且有：

(37)

當(dāng)隨機(jī)激勵輸入系統(tǒng)的能量與系統(tǒng)阻尼耗散的能量達(dá)到統(tǒng)計平衡時，有?p/?t=0，對應(yīng)的概率密度函數(shù)為平穩(wěn)概率密度函數(shù)pst(H)，其滿足如下的平穩(wěn)FPK方程：

L*pst(H)=0。

(38)

引入尺度函數(shù)l(u)與速度函數(shù)υ(u)：

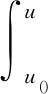
(39)

(40)

(41)

求得式(41)的平穩(wěn)概率密度函數(shù)為：

(42)

其中，參數(shù)e1、e2由邊界條件確定。

對于低強(qiáng)度噪聲激勵有e1=0[13]，則式(42)

可進(jìn)一步寫為：

(43)

應(yīng)用傳遞函數(shù)關(guān)系pst(b)=pst(H) ((d/dH)b)-1，得到基于變量b的平穩(wěn)概率密度函數(shù)為：

(44)

對平穩(wěn)概率密度函數(shù)式(44)在某一角度范圍[φ1,φ2]內(nèi)積分，可進(jìn)一步得到b(H)在該角度范圍內(nèi)的概率，從而對船舶的橫搖穩(wěn)定性進(jìn)行判斷。

4 計算結(jié)果與分析

4.1 船舶橫搖響應(yīng)

本文針對C11集裝箱船展開研究，該船主尺度如表1所示。

采用文獻(xiàn)[9]中所述的方法，在Φ∈[-0.6，0.6] rad、η∈[-10，10] m、Ψ∈[0，2π] rad范圍內(nèi)數(shù)值模擬C11集裝箱船的復(fù)原力臂GZ(Φ,η,Ψ)，得到不同Φ、η和Ψ時的復(fù)原力臂。采用GZa(Φ,η,Ψ)近似GZ(Φ,η,Ψ)，得到對應(yīng)式(2)的各項擬合系數(shù)為q1=2.164 3、q2=-1.775 3、q3=-0.106 1。

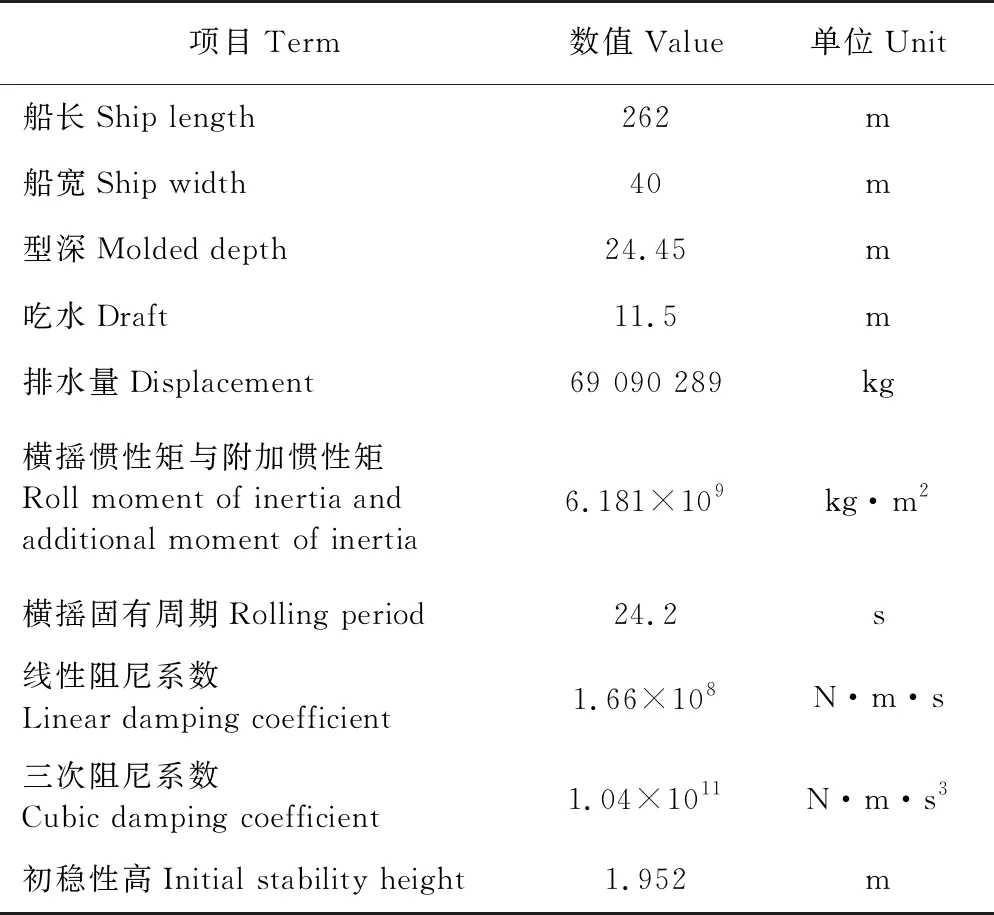
表1 C11集裝箱船主尺度[18]

本文研究采用ITTC海浪譜。對于特征波高3 m、特征波長262 m、航向角150°、航速1.43 m/s的情況，得到對應(yīng)于式(14)的船舶橫搖運動方程為：

(45)

取小參量取參量ε=0.1，得到對應(yīng)于式(15)的無因次橫搖運動方程為：

(46)

采用龍格庫塔法數(shù)值求解式(45)和式(46)，得到船舶橫搖角響應(yīng)時間歷程，如圖1所示。

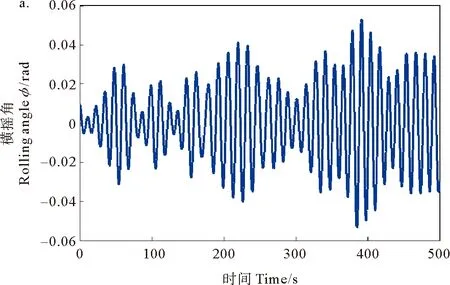
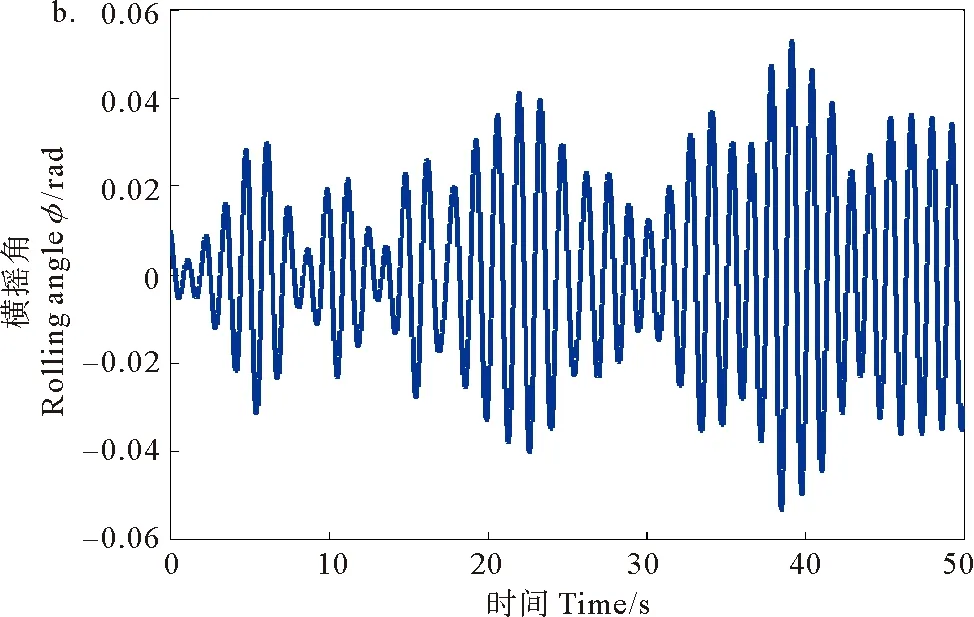
(a.時間尺度變換前 Before scale change;b.時間尺度變換后 After scale change.)

圖1 船舶橫搖響應(yīng)歷程

Fig.1 Time history of the ship rolling response

圖1表明，時間尺度變換前后，船舶橫搖響應(yīng)完全相同，驗證了對船舶橫搖方程進(jìn)行尺度變換的正確性。

4.2 概率密度函數(shù)的蒙特卡洛驗證

蒙特卡洛方法通過數(shù)值方法在計算機(jī)上模擬實際的響應(yīng)過程，然后進(jìn)行統(tǒng)計。該方法在系統(tǒng)可靠度評估、風(fēng)險評估及結(jié)構(gòu)非線性隨機(jī)動力響應(yīng)分析方面具有廣泛的應(yīng)用[19]。以下采用蒙特卡洛方法驗證本文理論計算概率密度函數(shù)的正確性。

蒙特卡洛法計算參數(shù)如下：隨機(jī)種子數(shù)n1=25、迭代步數(shù)n2=5 000 000、時間步長Δt=0.01 s，針對4.1中給出的海況，計算關(guān)于系統(tǒng)能量H的概率密度函數(shù)，并與采用隨機(jī)平均法計算得到結(jié)果進(jìn)行對比，如圖2所示。

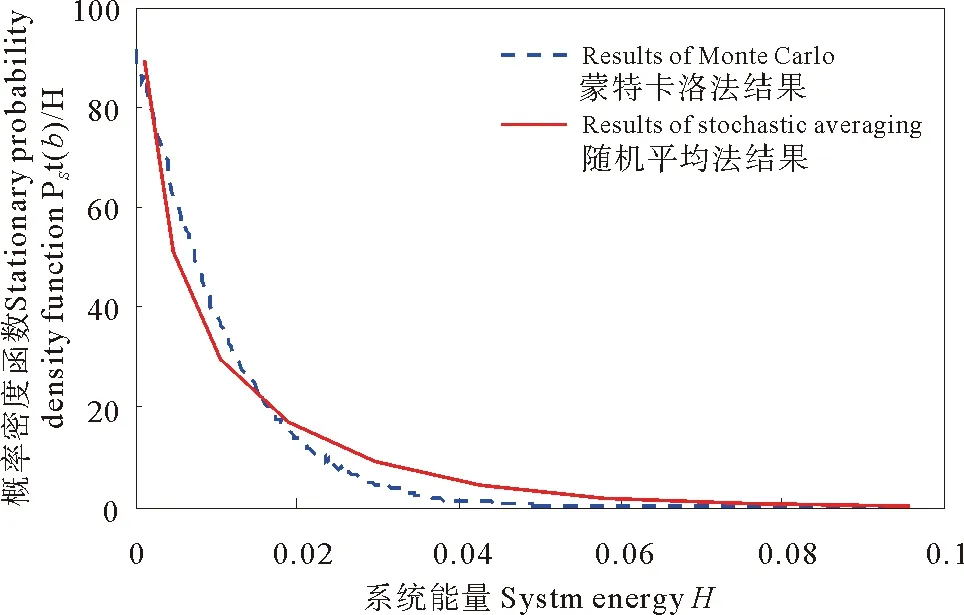
圖2 概率密度函數(shù)驗證

圖2表明，采用隨機(jī)平均法計算的概率密度函數(shù)與用蒙特卡洛法得到的概率密度函數(shù)吻合較好，驗證了本文理論推導(dǎo)及半解析計算方法的正確性。在第2節(jié)中，將隨機(jī)海況的波面升高近似為CARMA(2，1)過程，從而得到海浪的自相關(guān)函數(shù)，該函數(shù)是能量包線隨機(jī)平均法中漂移系數(shù)和擴(kuò)散系數(shù)的組成部分。由于近似擬合存在一定的誤差，因此在種子數(shù)足夠多的情況下，隨機(jī)平均法與蒙特卡洛法計算得到的概率密度函數(shù)仍會存在一定差別。

4.3 概率密度函數(shù)和概率

針對以上工況，由式(4)～(10)，可得到遭遇頻率下隨機(jī)過程η2(t)的譜密度函數(shù)，如圖3(a)所示。根據(jù)式(11)～(13)，應(yīng)用CARMA(2,1)過程擬合隨機(jī)過程η2，得到擬合的譜密度函數(shù)，如圖3(b)所示。得到擬合系數(shù)ci(i=1,2,3)和γ1如表2所示，計算得到不同工況關(guān)于b的概率密度函數(shù)，如圖4所示。

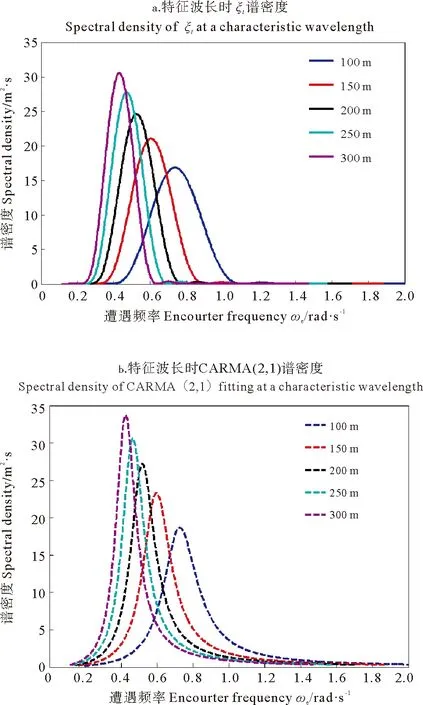
(a.由海浪普分解獲得 Obtained from the wave spectrum;b.由CARMA(2.1)過程擬合獲得 Obtained by CARMA(2.1) fitting.)

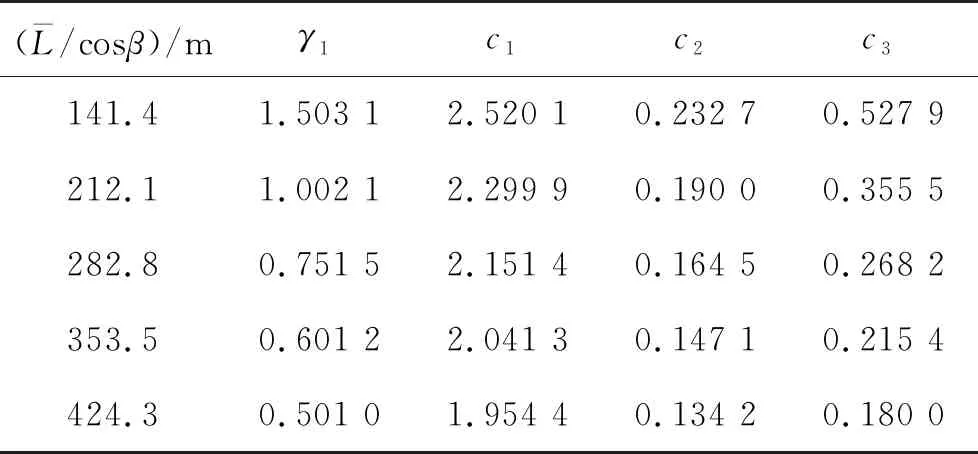
圖3 ξt的譜密度

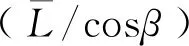
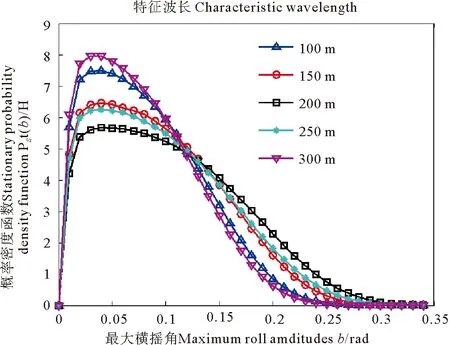
圖4 穩(wěn)定概率密度函數(shù)

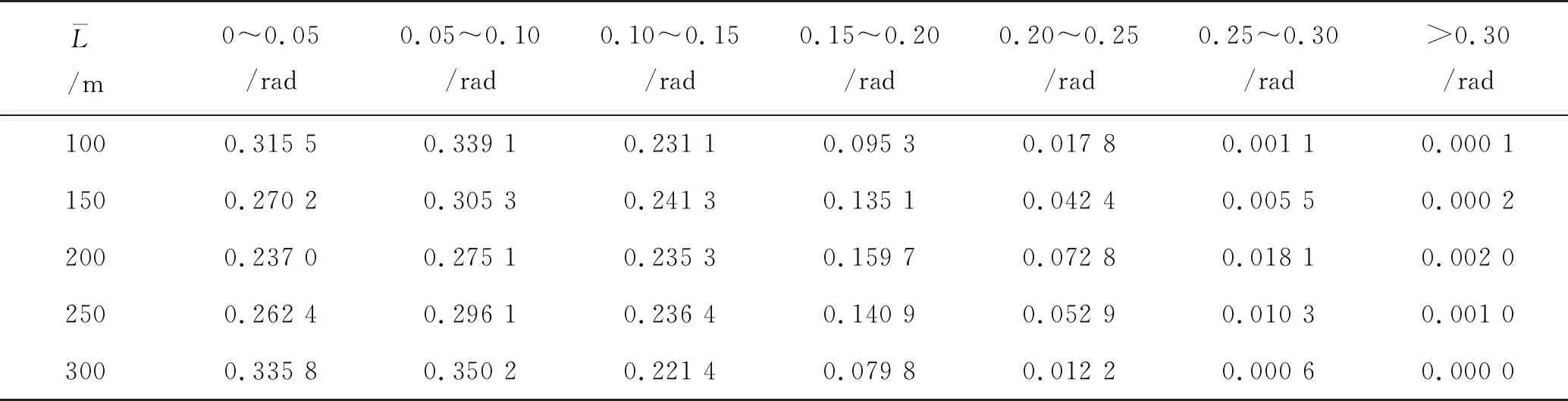
表3 b(H)在不同角度區(qū)間的概率

5 結(jié)語

本文基于能量包線隨機(jī)平均法，以C11船為例，半解析的研究了斜浪中船舶隨機(jī)參-強(qiáng)激勵橫搖響應(yīng)的概率密度函數(shù)及響應(yīng)概率。結(jié)果表明，當(dāng)遭遇頻率遠(yuǎn)離船長時，b(H)在大角度區(qū)間的概率較小；當(dāng)遭遇頻率接近船長時，b(H)在大角度區(qū)間的概率增加。由b(H)可定量分析斜浪中船舶隨機(jī)參-強(qiáng)激勵橫搖運動概率。