考慮自動駕駛儀延遲的多約束末制導律

趙國榮,李曉寶,劉 帥,趙超輪

(1.海軍航空大學參謀部， 山東 煙臺 264001； 2.海軍航空大學岸防兵學院， 山東 煙臺 264001)

導彈末制導律能夠?qū)崿F(xiàn)導彈對目標的精確打擊，同時考慮終端落角的約束，能夠使得導彈取得最佳毀傷效果[1]。攔截機動目標時，由于目標信息未知，傳統(tǒng)的比例導制導性能大大降低[2]，而滑模控制由于其對外部干擾和內(nèi)部不確定性有較強的魯棒性，應用在制導律設計中取得了良好的效果。

末制導中導彈為滿足落角要求，彈道通常較為彎曲，這可能導致目標不在導彈的導引頭視場范圍內(nèi)，使導彈丟失目標[3]。同時，導彈自動駕駛儀延遲也是影響制導精度的重要因素，因此，研究末制導律時同時考慮導彈落角和視場角約束并結(jié)合自動駕駛儀的延遲影響具有重要意義。文獻[4]基于切換邏輯的思路設計了帶有落角和視場角約束的終端滑模制導律，因為存在指令轉(zhuǎn)換的問題，制導律不是光滑連續(xù)的；文獻[5]利用積分型障礙Lyapunov函數(shù)設計了一種新型滑模制導律能同時約束落角和視場角，但積分項的引入使得制導律求解較為困難。文獻[6]考慮了導彈的一階自動駕駛儀延遲問題，而研究導彈的二階動態(tài)特性更貼近實際情況。文獻[7-8]進一步給出了考慮自動駕駛儀二階動態(tài)和攻擊角度約束的制導律設計方法。然而，文獻[6-8]都沒有考慮了視場角約束的問題。

本文結(jié)合導彈自動駕駛儀的二階動態(tài)特性提出了一種帶有落角和視場角約束的末制導律。通過構(gòu)造一種新型的滑模面并結(jié)合動態(tài)面控制給出了制導律的設計方法；利用一種新的障礙Lyapunov函數(shù)并根據(jù)Lyapunov穩(wěn)定性理論，證明了制導系統(tǒng)的彈目視線(line of sight，LOS)角跟蹤誤差和LOS角速率是收斂的，并且視場角始終滿足約束條件。

1 問題描述和相關引理

1.1 問題描述

如圖1所示,假定末制導過程中導彈和目標的速度VM和VT大小不變，r和q分別表示為彈目之間的相對距離和LOS角，φM和φT分別表示為導彈和目標的前置角，γM和γT分別表示為導彈和目標的航跡角，aM和aT分別表示為導彈和目標的法向加速度。導彈和目標的末制導運動學關系為

(1)

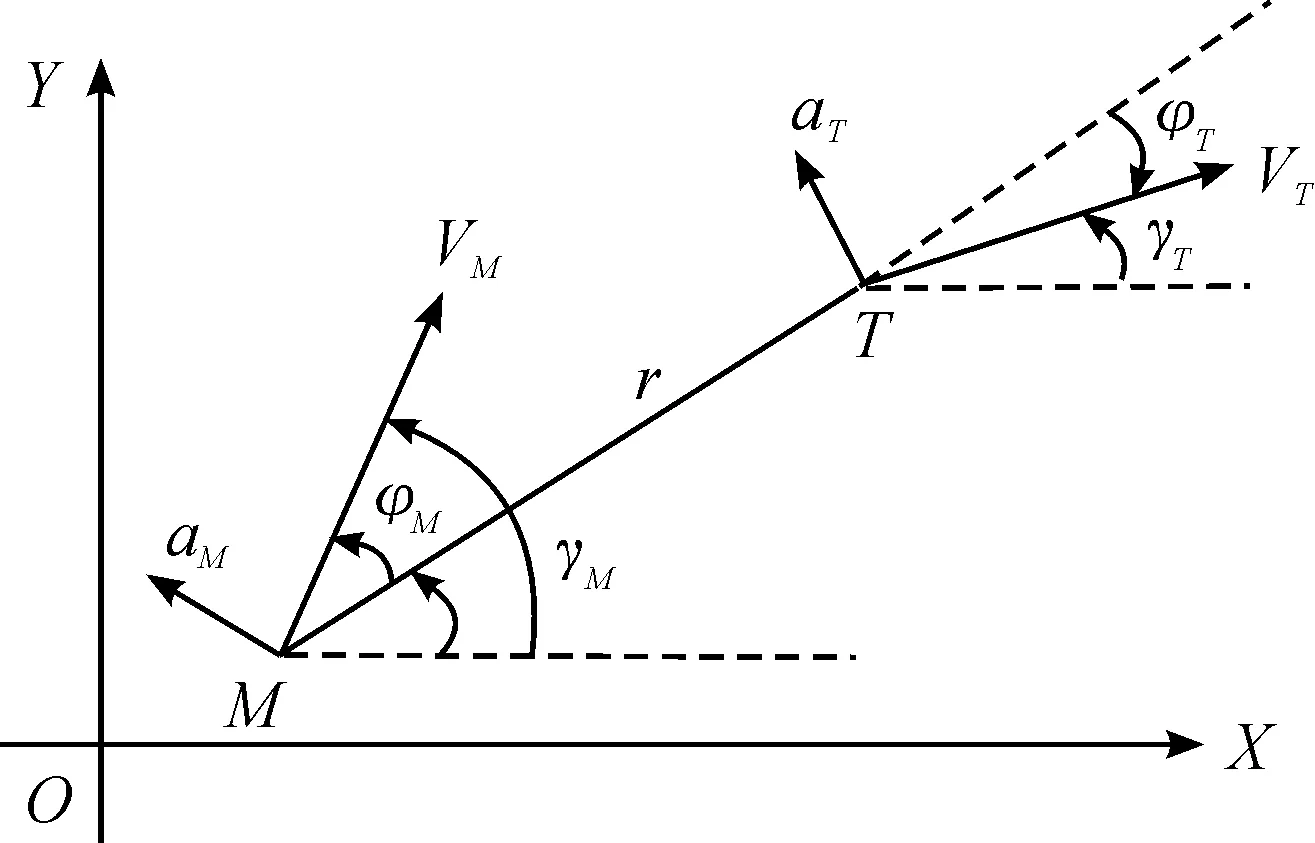
圖1 彈目關系

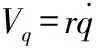
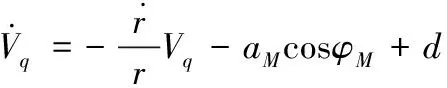
(2)

其中，d=aTcosφT。

假設1若存在一個有界常數(shù) Δ≥0 代表目標加速度aT的最大值，可知 |d|≤Δ。

導彈的自動駕駛儀的動態(tài)特性可以看成二階慣性環(huán)節(jié)：

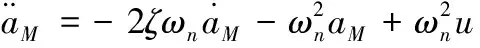
(3)

其中，u為導彈自動駕駛儀的輸入指令，ζ和ωn分別代表導彈自動駕駛儀的阻尼比和固有頻率。

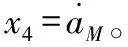
(4)

針對捷聯(lián)導引頭，在攻角近似為零的情況下，可采用前置角φM來表示導彈的視場角。若導彈可接受的最大視場角為φmax，本文末制導律的設計要求就是通過制導指令u使LOS角誤差x1以及垂直于LOS方向的相對速度分量x2最終收斂到零，確保導彈能夠以給定的落角qd準確命中目標，并且保證導彈視場角始終滿足 |φM|≤φmax。

根據(jù)式(1)可得 |φM|≤φmax成立的充分條件為

|x2|≤α

(5)

其中，α=VMsinφmax-VT。

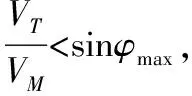
1.2 基本引理

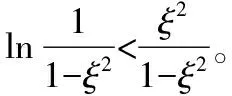
引理2[10]對任意的正數(shù)α，令A={x∈R∶|x|<α{ 以及B=Rl×A?Rl+1均為開區(qū)間，考慮如下系統(tǒng)：

(6)

其中，η=[ω,x]T∈B，函數(shù)h∶R+×B→Rl+1在時間t上分段連續(xù)，并且關于x滿足局部一致Lipschitz條件。若函數(shù)U∶Rl→R+以及V1∶A→R+在各自的定義域內(nèi)連續(xù)可微且是正定的，同時滿足：當 |x|→α時，V1(x)→∞ ；γ1(||ω||)≤U(ω)≤γ2(||ω||)，γ1和γ2為K∞類函數(shù)。那么，對于函數(shù)V(η)=V1(x)+U(ω) 以及初時狀態(tài)x(0)∈A，假設不等式滿足如下關系

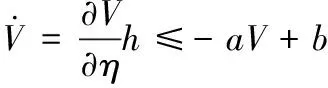
(7)

其中a,b>0，則對任意t∈[0,∞)，都滿足x∈A。

2 考慮自動駕駛儀延遲的帶有落角和視場角約束的制導律

2.1 制導律的設計

1) 設計虛擬控制量x3c

構(gòu)造如下滑模面

s1=x2+α(1-e-β|x1|)sign(x1)

(8)

對其求導可得

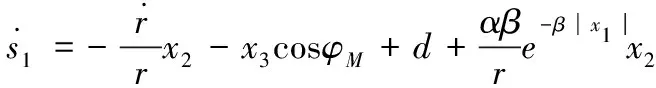
(9)

虛擬控制量x3c設計如下：

(10)

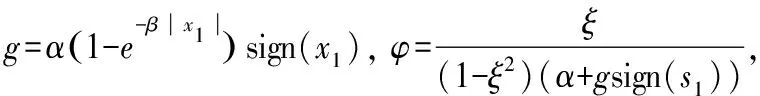
為了避免逆推設計方法的項數(shù)爆炸問題，引入一個一階濾波器對虛擬控制量x3c進行濾波：

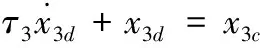
(11)

其中，τ3>0 為濾波器設計參數(shù)，x3d(0)=x3c(0)。

定義邊界層誤差：

y3=x3d-x3c

(12)

2) 設計虛擬控制量x4c

定義跟蹤誤差變量

s2=x3-x3d

(13)

對其求導可得

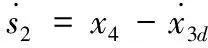
(14)

虛擬控制量x4c設計如下：

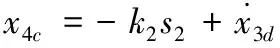
(15)

通過一個一階濾波器對虛擬控制量x4c進行濾波

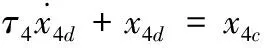
(16)

其中，τ4>0 為濾波器設計參數(shù)，x4d(0)=x4c(0)。

定義邊界層誤差

y4=x4d-x4c

(17)

3) 設計制導指令u

定義跟蹤誤差變量

s3=x4-x4d

(18)

對其求導可得

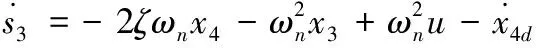
(19)

導彈制導指令u可設計如下

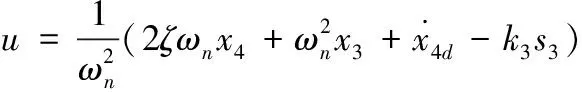
(20)

進一步，將式(11)、式(13)、式(15)、式(16)、式(18)代入式(10)可得

(21)

2.2 穩(wěn)定性分析

定理1對于制導系統(tǒng)式(4)，如果制導指令u設計為式(21)，并且狀態(tài)變量x2滿足約束條件 |x2|<α，則導彈最終能夠成功的攔截目標，并且狀態(tài)變量x1,x2收斂于零。

證明：該定理證明過程如下：

構(gòu)造如下障礙Lyapunov函數(shù)：

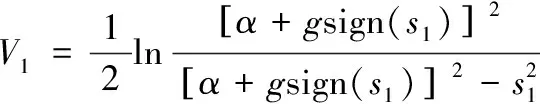
(22)

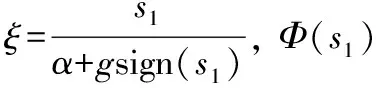
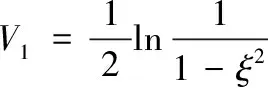
(23)

因為 |x2|<α，可知 |s1|<α+gsign(s1)，即 |ξ|<1。

對V1求導并代入式(9)、式(10)、式(12)、式(13)可得：

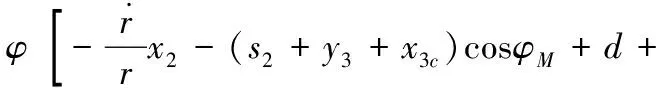
φ[d-Δsign(s1)-k1s1-φ-(s2+y3)cosφM]

(24)

根據(jù)YOUNG不等式可得：

(25)

(26)

根據(jù)假設1以及引理1得：

φ[k1s1+φ+(s2+y3)cosφM]≤

φ[-k1s1-φ-(s2+y3)cosφM]≤

(27)

構(gòu)造如下Lyapunov函數(shù)：

(28)

對其求導并代入式(14)、式(17)、式(18)可得：

(29)

構(gòu)造如下Lyapunov函數(shù)：

(30)

對其求導并代入式(19)、式(20)可得：

(31)

構(gòu)造如下Lyapunov函數(shù)：

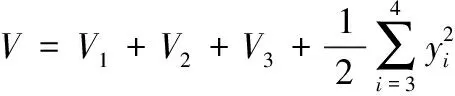
(32)

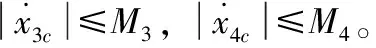
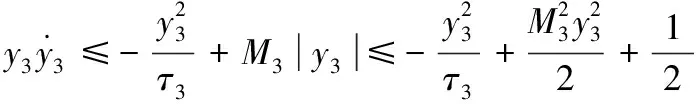
(33)

(34)

對Lyapunov函數(shù)V求導可得

-2k1V1+(3-2k2)V2+(1-2k3)V3+

(35)

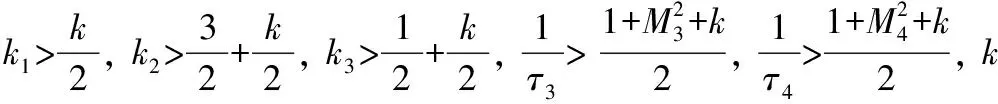
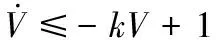
(36)

求解式(36)得：

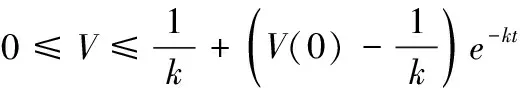
(37)

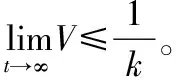
當制導系統(tǒng)的狀態(tài)量x1,x2到達滑模面s1=0 時，由式(8)可知x1x2≤0，并且

|x2|=α(1-e-β|x1|)

(38)

構(gòu)造如下Lyapunov函數(shù)

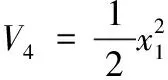
(39)

對其求導可得

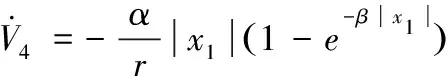
(40)

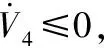
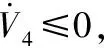
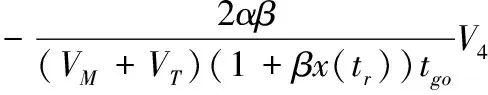
(41)

求解上述不等式可知

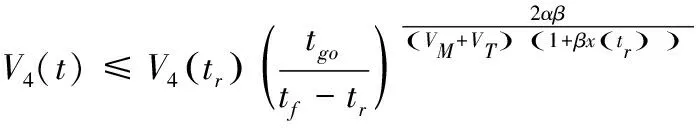
(42)

定理2假設末制導初始條件滿足 |x2(0)|<α，那么，在制導律(21)的作用下末制導狀態(tài)變量x2始終滿足約束 |x2|<α。

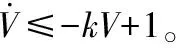
狀態(tài)變量x1,x2在到達滑模面s1開始滑動時，由s1=0，可知 |x2|=α(1-e-β|x1|)≤α。證畢。

注1因為符號函數(shù) sign(s1) 的存在，制導律(21)中x3c是非連續(xù)的，可能會引發(fā)顫振現(xiàn)象。為此，用Sigmoid函數(shù)近似替代符號函數(shù) sign(s) ：

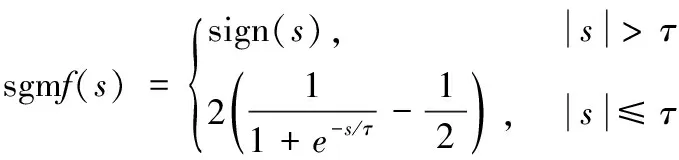
(43)

3 仿真分析

假設導彈的初始位置為(-5 000 m,0)，目標的初始位置為(0,0)，初始航跡角γM0=0 °，γT0=100 °，導彈和目標的速度分別取值VM=200 m/s，VT=40 m/s，目標的機動aT=gcos(πt/4)。制導律(31)中的參數(shù)選取為ζ=0.8，ωn=20，β=10， Δ=10，k1=2，k2=k3=10，τ3=τ4=τ=0.01，導彈最大加速度取 20g，重力加速度g=9.8 m/s2。

3.1 以不同落角和視場角約束打擊目標

假設導彈最大視場角φmax分別為45°，60°，期望的落角qd分別為-40°，-60°，采用制導律式(21)在3種不同約束條件下進行仿真，結(jié)果如圖2所示。

圖2(a)表明：當φmax和qd變化時，導彈均能夠成功攔截目標，并且φmax和qd越大，彈道曲線越彎曲。圖2(b)給出了導彈加速度曲線圖，可以看出三種不同約束情況下的加速度曲線都較為光滑平緩，不存在指令跳變。圖2(c)表明：LOS角q最終都能夠收斂到期望的落角qd，使得導彈滿足落角約束的要求。圖2(d)給出了導彈視場角φM的變化曲線，可以看出當限定最大視場角φmax時，在制導律式(21)作用下導彈始終能夠在視場角范圍內(nèi)實現(xiàn)對目標的精確攔截。

3.2 與制導律FISMG，ISMDSG對比

文獻[6]采用切換邏輯的思路設計的一種帶有落角和視場角約束的制導律FISMG，但其沒有考慮導彈自動駕駛儀影響；文獻[10]設計了一種帶有二階自動駕駛儀動態(tài)特性和攻擊角度約束的制導律ISMDSG。假設導彈最大視場角φmax為45°，期望的落角qd分別為-60°，為了充分分析制導律式(21)的制導性能，在相同的場景下，對3種制導律進行仿真，結(jié)果如圖3所示。

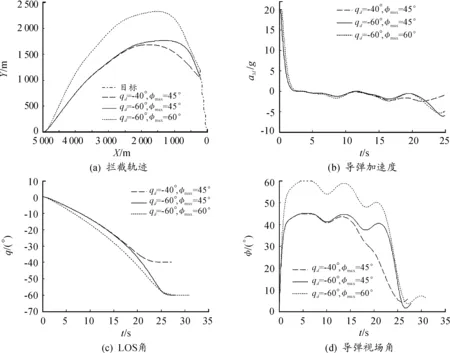
圖2 不同落角和視場角約束下的末制導仿真

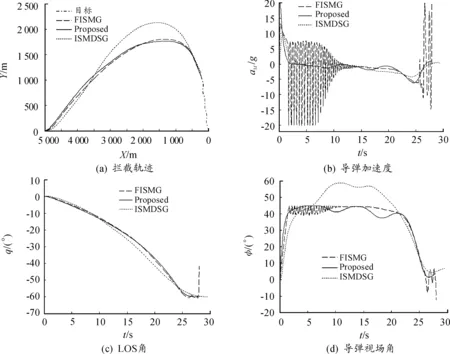
圖3 不同末制導律仿真

圖3(a)給出了制導律式(21)和FISMG，ISMDSG末制導軌跡曲線，通過仿真得出三者的末制導時間分別為27.92 s，28.01 s和29.54 s，對應的脫靶量分別為0.012 4 m，0.664 9 m，0.002 4 m。通常情況下末制導終端彈目相對距離rf滿足rf≤0.25 m時，認為末制導是成功的。因此，制導律式(21)以及ISMDSG能夠使導彈成功攔截目標，并且制導律式(21)使導彈的末制導時間最短，而FISMG使導彈的末制導過程失效，這是因為FISMG是在導彈自動駕駛儀理想情況下設計的，當考慮導彈的自動駕駛動態(tài)特性時，F(xiàn)ISMG的制導性能大大降低，甚至失效。

圖3(b)表明：當考慮導彈自動駕駛儀動態(tài)時，F(xiàn)ISMG使得導彈的加速度出現(xiàn)了嚴重的震顫現(xiàn)象，并且制導律在設計過程中會存在指令跳變的問題，F(xiàn)ISMG采用了一種特殊的方法來“軟化”這一問題。而制導律式(21)和ISMDSG的加速度指令曲線光滑平緩。從圖3(c)中可以看出制導律式(21)相比于ISMDSG使得LOS角能夠在更短的時間內(nèi)收斂到期望的落角qd，而FISMG對應的LOS角曲線在末端出現(xiàn)了發(fā)散的現(xiàn)象，最終不能使導彈滿足落角約束的要求。圖3(d)表明制導律式(21)和FISMG使得導彈在末制導過程中始終滿足視場角約束的要求，并且制導律式(21)的視場角曲線光滑，而FISMG因為導彈加速度的變化而使得視場角在前期和末期產(chǎn)生了較大的抖動。ISMDSG因為在設計過程中沒有考慮視場角約束，導致導彈在ISMDSG作用下超出了視場角約束范圍，視場角最大值接近60°。

4 結(jié)論

本文在考慮導彈自動駕駛儀二階動態(tài)特性的影響下設計了一種滿足落角和視場角約束的新型制導律。所設計的制導律不存在指令跳變。結(jié)合滑模控制理論與動態(tài)面方法，從理論上嚴格證明了制導系統(tǒng)在該制導律作用下最終保持穩(wěn)定，并且視場角在整個末制導過程中始終滿足約束條件。仿真實驗表明：在新設計的制導律作用下，導彈能夠以不同的落角和不同的視場角約束準確的打擊目標，與其他制導律的對比，本文所設計的制導律具有更加優(yōu)越的制導性能。為了提高制導律精度，應采用更加精確的三維末制導模型，并且考慮視線俯仰運動和視線偏航面運動之間的耦合關系。如何在本文提出的制導方法基礎上設計三維空間內(nèi)的末制導律，值得進一步研究。