基于ADAMS的衛星對接機構球鎖裝置動力學分析

王昊東，楊 臻，武國梁

(1.中北大學 機電工程學院，太原 030051；2.西南自動化研究所，四川 綿陽 621000)

空間對接技術是發展空間對抗裝備的重要手段，是各航天大國爭相發展的核心技術[1]，是實現航天器在軌裝配、回收、補給、維修、以及航天員交換等在軌服務的先決條件[2-3]。空間對接機構作為實現兩航天器在軌對接的核心部件，對兩航天器的對接、鎖緊、分離成功起著至關重要的作用[4]。

隨著模塊化航天器[5-6]設計概念被提出，以及電子、控制技術的不斷進步，小型航天器在軌重組對接技術以其功能可拓展、發射成本低、使用壽命久的優點成為空間技術發展的主流[7-8]。傳統空間對接機構如錐桿式、類錐桿式[9]和異體同構周邊式等對接機構結構過于龐大，且利用推力器實施慣性對接的方式無法適用于小型衛星的在軌對接。2011年英國薩里大學提出由電磁力提供對接力/分離力，用于小型模塊衛星在軌組裝的AAReST的項目[10]。其對接機構因小型化設計而采用反對稱原則[11]，由對接系統的主動機構(錐頭)和被動機構(錐口)聯合完成對接。目前該項目處于地面實驗階段，而我國對于小型衛星對接機構的研究尚處于理論階段。在各國空間技術對抗的背景下，國內開展小型衛星對接機構的研究刻不容緩。

總結薩里大學電磁對接機構：該機構無結構鎖設計，在自鎖時需時刻通電保持電磁引力。現以電磁力為對接力的前提下，設計一種小型衛星對接機構，采用球鎖裝置機械鎖緊形成剛性連接，鎖緊后可斷電減少能源消耗。利用虛擬樣機技術針對電磁對接機構進行結構設計和仿真分析，從而為電磁對接機構原理樣機的建立提供參考。

1 機構的組成

對接機構總體結構的UG模型如圖1所示。

1主動電磁鐵；2對接引導錐；3主動機構對接齒；4主動機構球鎖孔；5引導錐口；6被動機構對接齒；7轉動鎖緊圈；8捕獲鎖彈簧頂銷；9齒輪；10鎖緊球；11被動電磁鐵

圖1 對接機構總體結構UG模型

2 工作原理

2.1 電磁力與接近過程

環形電磁線圈是電磁對接系統的基本組成部件，目前提出的空間電磁對接系統主要利用一組環形電磁線圈組成的電磁鐵在空間相互作用產生電磁力和力矩，實現兩星的對接。下面通過電磁場仿真軟件Ansoft Maxwell在麥克斯韋方程基礎上進行電磁鐵的電磁場仿真，電磁鐵的具體參數值見表1，電磁場仿真模型如圖2所示。

表1 電磁鐵參數值

圖2 電磁場仿真模型

以衛星質量100 kg進行仿真，得出一對電磁鐵在不同距離時，相互之間產生的電磁引力。如圖3所示，兩電磁鐵距離越小，電磁引力增加程度越大。

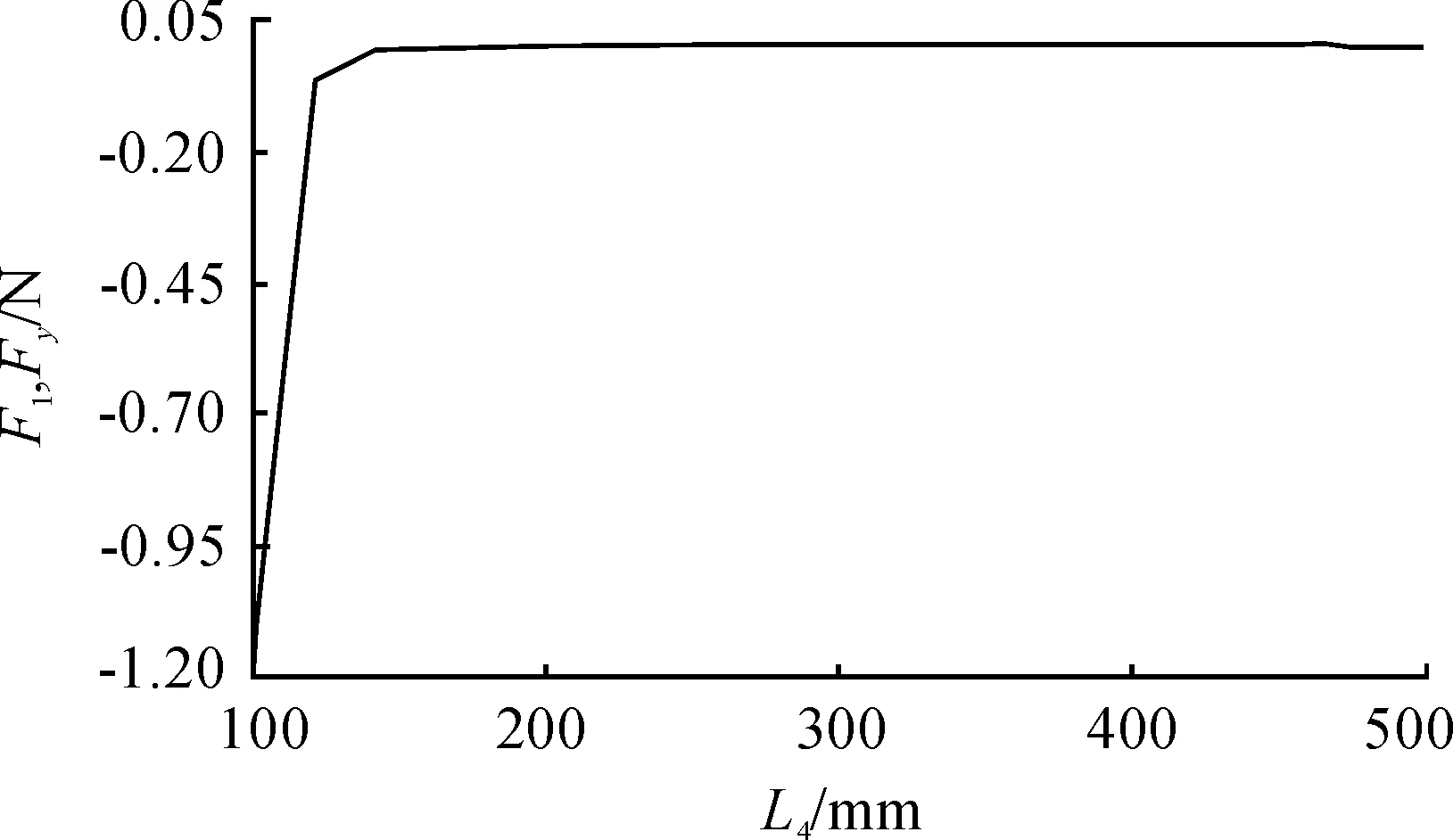
圖3 不同距離時的電磁引力

主、被動機構的對接過程靠近階段：以對接距離0.5 m的一維對接(或對接軸角度小于15°)為例，表2的數據為根據電磁引力仿真結果，每100 mm距離取點選取數據，考慮精度要求得出瞬時電磁力。將表2 中的數據代入牛頓第二定律計算得出對接速度曲線如圖4。0～133.8 s電磁鐵全功率工作，主、被動機構在電磁引力作用下加速靠近，加速時間133.8 s，對接速度達到0.033 m/s；133.8～135.5 s期間，電磁鐵減小電流，使電磁引力維持1 N，機構勻加速靠近，135.5 s時速度增至0.05 m/s；135.5～135.8 s期間關閉電磁鐵，主、被動機構勻速靠近至接觸，135.8 s時兩機構接觸瞬時速度小于0.1 m/s；預計靠近階段總耗時不少于136 s。

2.2 鎖緊機構

對接機構依靠電磁力的引力作用靠近、接觸，使用球鎖裝置進行捕獲、鎖緊、解鎖，最后在電磁鐵斥力作用下分離。對接過程的工作流程框圖如圖5所示。

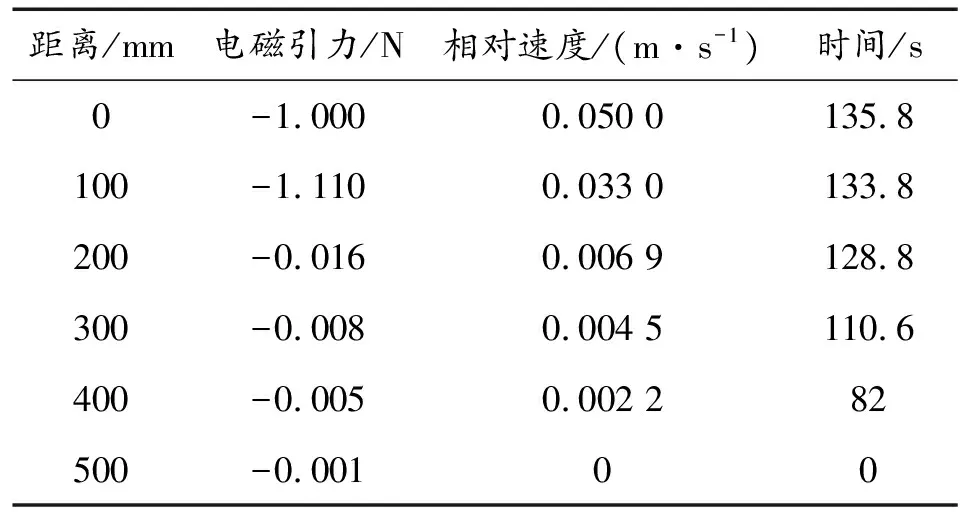
表2 不同距離的電磁引力、相對速度大小

圖4 不同距離對接速度曲線

圖5 對接過程工作流程框圖

其中鎖緊機構工作過程分為初對準、捕獲鎖捕獲主動機構、電機驅動鎖緊圈轉動完成鎖緊、電機驅動鎖緊圈轉動解鎖4個過程：

1) 主動衛星與被動衛星在0.5～1 m距離時啟動電磁鐵，在相互之間的電磁引力作用下靠近，期間通過對電磁力大小、方向的控制完成慢速接近，使兩衛星接觸時無沖擊；接觸后，在對接引導錐、錐口的引導下完成軸向上的初對準；

2) 捕獲主動機構示意圖如圖6。當主動機構插入被動機構時，主動機構對接齒與被動機構對接齒形成精對準嚙合，同時捕獲鎖彈簧頂銷將鎖緊球壓入主動機構球鎖孔完成捕獲鎖對主動機構的捕獲；

3) 鎖緊狀態示意圖如圖7。齒輪在電機驅動下帶動鎖緊圈轉動至鎖緊位，鎖緊圈內壁將鎖緊球與鎖孔之間壓緊，完成對接機構的剛性連接。此時主動、被動電磁鐵可斷電，連接的衛星開始執行在軌任務。

圖6 捕獲主動機構示意圖

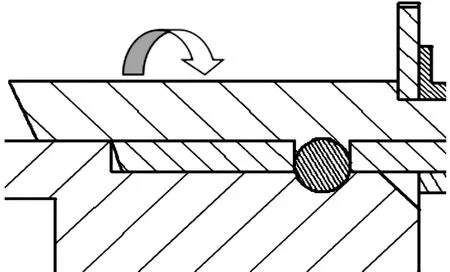
圖7 鎖緊狀態示意圖

4) 完成在軌任務(維修、補給、組裝等任務)后，連接的兩衛星進行釋放分離：電機繼續驅動，帶動鎖緊圈轉至解鎖位，鎖緊圈內壁(如圖8所示)的鎖緊球釋放槽釋放鎖壓緊的鎖緊球，使對接機構處于解鎖狀態(示意圖如圖9)。

解鎖后，主動、被動電磁鐵通電形成相互之間的斥力，利用斥力完成分離。分離后，電機可繼續驅動鎖緊圈轉動至彈簧頂銷位置，為下一次對接作好捕獲鎖準備。

圖8 鎖緊圈內壁

圖9 解鎖狀態示意圖

3 對接機構球鎖裝置動力學分析

通過建模軟件UG對整個對接機構進行三維建模，模型參數值如表3。將模型導入ADAMS，按照實際情況對零部件進行材料、約束、接觸力的添加，并設置變量參數，然后進行動力學仿真。

表3 模型參數值

對接機構的運動和受力較為復雜，對模型進行適當簡化和假設能將復雜問題有效地簡單化，有利于運動的分析[12]：

1) ADAMS動力學模型按照實際的運動規律添加約束，其模型不考慮各種誤差[13]；

2) 將所有零部件視為剛體[14]；

3) 重力加速度為零；

4) 不參與運動過程碰撞的零部件進行布爾加和操作，作為一個零部件處理[15]。

仿真主要針對鎖緊與釋放2個功能進行。主動機構沿Z軸運動，首先驗證機構是否能順利完成對接功能；其次驗證主被動機構之間完成鎖緊后，在主動機構受200 N軸向反向外力下，分析結構是否可靠，能否完成自鎖；以及分析對接過程中鎖緊球與主動機構鎖孔的接觸力、鎖緊球與鎖緊圈接觸力。

設置對接力大小，鎖緊圈轉動角度并運行軟件：

1) 主動機構對接力大小時間函數：step(time,0.28,0,0.281,30)+step(time,0.3,0,0.35,70)+step(time,0.39,0,0.4,-100)+step(time,1.6,0,1.7,-200)+step(time,2.7,0,2.8,200)+step(time,4,0,4.1,-80)；

2) 鎖緊圈轉動角度時間函數：step(time,0.5,0 d,1.5,45 d)+step(time,2.9,0 d,3.9,45 d)；“d”為角度(°)。

設置動力學仿真時長4.13 s；被動機構與空間設置固定副，主動機構設移動副模擬對接過程中快速接近段、慢速接近段；以對接力控制主、被動機構接觸后的對接/分離過程，得出仿真結果曲線如圖10～圖14。

圖10中實線為主動機構軸向位置變化曲線，虛線為主動機構速度變化曲線；圖11實線為鎖緊圈以機構軸向為軸的轉動角速度，角速度曲線對時間求積分得出角度變化曲線，即虛線；結合圖10圖11分析：圖10中，0～0.1 s主動機構快速靠近速度為1 m/s；0.1～0.26 s期間以0.1 m/s的速度慢速靠近；0.26～0.36 s期間接觸碰撞，主動機構速度因機械振動產生波動，主動機構總行程130.25 mm；圖11中，0.36～4 s期間主、被動機構接觸，位移、速度基本保持不變，其中0.5～1.5 s鎖緊圈由0°轉動至45°鎖緊狀態，1.5～2.9 s保持鎖緊狀態不變，2.9～3.9 s鎖緊圈由45°轉動至90°解鎖狀態(圖11)，因進行鎖緊/釋放動作，機械振動效果在主動機構速度曲線中反映出來(圖10)；4～4.1 s，鎖緊裝置解鎖，釋放主動機構加速分離。

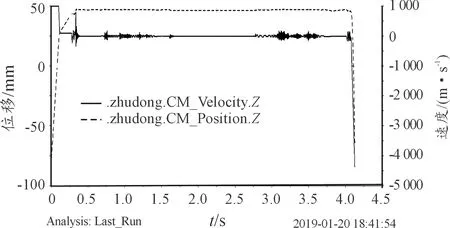
圖10 主動機構的軸向位移、速度曲線

圖11 鎖緊圈的轉動角速度、轉動角度曲線

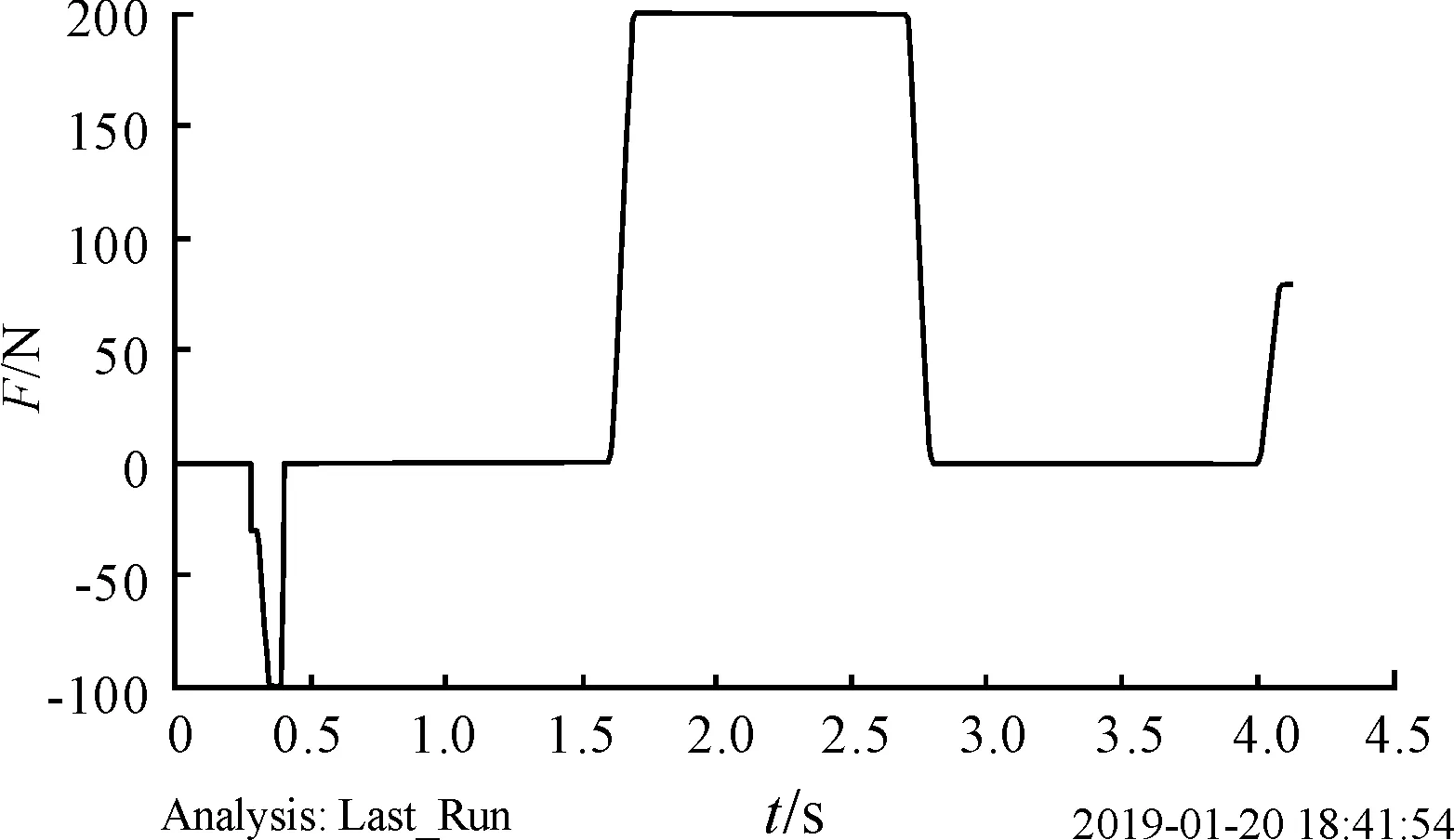
圖12 主動機構對接/分離力曲線

圖13 鎖緊圈與1號鎖緊球接觸力曲線

圖14 鎖孔與1號鎖緊球接觸力曲線

圖12所示為提前設置的主動機構對接/分離力數值曲線，0.26～0.4 s對接力為100 N；主、被動機構接觸后0.5～1.6 s期間和2.6～4 s期間無力作用；1.6～2.6 s期間添加200 N軸向反力，以驗證鎖緊機構可靠性；4～4.1s分離力增加至70N。圖13所示曲線為主、被動機構接觸并完成一系列動作后，鎖緊圈與一號鎖緊球與之間的接觸力數值曲線；圖14所示為主動機構鎖孔與一號鎖緊球之間的接觸力數值曲線；

結合圖12圖13圖14分析：0～0.5 s鎖緊球與鎖緊圈不接觸，鎖緊球在彈簧頂銷的作用下與主動機構接觸碰撞，接觸力為16.3N；0.5～1.5 s鎖緊圈轉動并與鎖緊球接觸，接觸力平均值為247.2 N，最高達到810.4 N，鎖緊球與鎖孔接觸力平均值為62.1 N，最高達到346.2 N；1.5～2.8 s主、被動機構受200 N軸向反力，鎖緊球與鎖緊圈接觸力平均值為55.8 N，鎖緊球與鎖孔接觸力平均值為73.2 N；2.8～3.8 s，鎖緊圈與鎖緊球接觸力平均值為139.4 N，最高達到772.6 N，鎖緊球與鎖孔接觸力平均值為62.4 N，最高達到250.2 N；3.8～4.13 s兩機構解鎖至分離，鎖緊球不與鎖緊圈和鎖孔接觸，接觸力均為0 N。

通過結果分析出：主、被動機構以0.1 m/s的對接速度接觸后，能在0.9～1.1 s內順利完成鎖緊或解鎖；因鎖緊圈與鎖緊球之間存在有間隙和無間隙的切換，所以在鎖緊圈轉動時，與鎖緊球間存在碰撞產生較大瞬時接觸力，應增加鎖緊圈內壁與鎖緊球的接觸面積，并增加鎖緊圈內壁硬度，或適當減慢鎖緊圈的轉動速度，使碰撞減弱；在鎖緊狀態下，機構受200N軸向反力時，鎖緊球與鎖緊圈和鎖孔之間的接觸力在55～74 N之間，屬于正常值，說明鎖緊裝置在受200 N拉力下，可保持正常的鎖緊狀態。

3.3 鎖緊球

通過鎖緊圈壓緊被動機構和主動機構鎖孔之間的鎖緊球，受到的剪切力和鎖緊球的強度決定了鎖緊可靠性。

面積：

鎖緊球的直徑為5.6 mm，鎖緊狀態下鎖緊球截面面積遠大于Smin，即鎖緊球強度滿足要求。

4 結論

設計了適用于小型衛星的電磁對接機構的球鎖式鎖緊裝置：

1) 對接機構在0.5 m距離內可利用電磁鐵引力進行靠近、對接；

2) 球鎖裝置能順利完成鎖緊與解鎖動作；

3) 仿真結果為建立原理樣機及電磁控制策略制定提供參考。