彈道解算中網(wǎng)格化氣象數(shù)據(jù)的計算機通報研究

賈望屹，李 巖，于佳興

(1.中國電子科技集團公司第二十研究所， 西安 710068； 2.南京理工大學 能源與動力工程學院， 南京 210094)

隨著武器射程的提高，氣象因素已經(jīng)成為影響射擊精度的重要因素[1-3]。除了受探測設(shè)備精度影響的氣象諸元誤差，還有氣象條件隨時空變化的誤差[4-5]。但是傳統(tǒng)氣象保障中無論是通過GPS、無線經(jīng)緯儀還是探空雷達進行氣象觀測，都只能獲得探測位置隨高度變化的一組氣象數(shù)據(jù)，難以反映氣象條件隨彈丸外彈道區(qū)域的變化。而數(shù)值氣象預(yù)報是一種通過數(shù)值計算提供未來一段時間內(nèi)網(wǎng)格化氣象數(shù)據(jù)的方法，能夠彌補傳統(tǒng)氣象保障的不足，是國外遠程武器氣象保障中興起的重點研究方向之一[6-7]。國內(nèi)于立等[8]，探究了通過數(shù)值氣象預(yù)報獲取彈道區(qū)域的預(yù)報數(shù)據(jù)，并分析了對彈丸射程和側(cè)偏的影響，但是沒有涉及預(yù)報氣象數(shù)據(jù)的處理方法。傳統(tǒng)氣象數(shù)據(jù)處理中，一般由氣象分隊將探測獲得的氣象數(shù)據(jù)編制成計算機通報[9-11]。計算機通報可在彈道解算中直接插值使用，但對于多組氣象數(shù)據(jù)如何使用研究較少。針對多組氣象數(shù)據(jù)在彈道中的使用這一問題，張志遠等[12]研究了將彈道分成多段分別使用對應(yīng)段計算機通報的方法，雖然在彈道區(qū)域內(nèi)增加了氣象探測點，相比于只使用一個探測點氣象數(shù)據(jù)概括整個彈道區(qū)域的氣象變化有了較大提高。但是要使用氣象數(shù)據(jù)越多就要對彈道分更多段，對于網(wǎng)格化氣象數(shù)據(jù)在彈道解算中使用難以直接使用。因此研究網(wǎng)格化氣象數(shù)據(jù)在計算機通報中處理的方法，既能在通報中反映氣象隨空間的變化，也可以直接在彈道解算中使用，在實際作戰(zhàn)中意義重大。

1 彈道網(wǎng)格化氣象數(shù)據(jù)的方案選擇和數(shù)據(jù)處理

1.1 WRF模式的方案選擇

WRF模式由Fortran語言編寫，具有靈活性強、易于維護、在Linux或Unix等系統(tǒng)中都能運行。其研制的成功為氣象學研究帶來很大便利，如今在中小尺度數(shù)值氣象預(yù)報中廣泛使用。與氣象學中關(guān)注的重點不同，為彈道解算提供氣象保障，需要風速、風向、氣溫、氣壓等氣象因素的具體值，而非氣象學中關(guān)注的最值或平均值等。此外氣象學領(lǐng)域?qū)τ谌粘Ｇ绾锰鞖怅P(guān)注較少，主要原因在于晴好天氣中各因素與極端天氣相比變化較小，但是現(xiàn)階段武器的氣象保障中主要對非極端天氣進行探測。

采用四層嵌套網(wǎng)格數(shù)分別為79×77、91×91、112×112、130×130。平面網(wǎng)格分辨率分別為27 km、9 km、3 km、1 km。根據(jù)彈丸對風速要求較高的特點確定WRF模式參數(shù)化方案：微物理方案為簡單表示雨水的產(chǎn)生、降落蒸發(fā)、云水增長等過程的Kessler方案，積云參數(shù)化方案為簡單包含水汽抬升和下沉運動的云模式的Kain-Fritsch方案，邊界層參數(shù)化方案為采用了穩(wěn)定函數(shù)計算地面熱量等交換系數(shù)，利用對流速度加強地面熱量和濕度的通量的MYJ方案，輻射方案為Dudhia短波輻射和RRTM長波輻射方案，近地面層參數(shù)化方案采用MM5相似方案，陸面過程采用考慮了地面發(fā)射體性質(zhì)的Noah陸面過程方案。

1.2 彈道區(qū)域內(nèi)氣象的確定方法

由于數(shù)值氣象預(yù)報提供氣象保障，提供的是預(yù)報數(shù)據(jù)，在發(fā)射之前，對于彈道區(qū)域內(nèi)某點的實際氣象數(shù)據(jù)，與預(yù)報點之間并不一定重合，因此對于任意點氣象數(shù)據(jù)的確定，可以采用對該平面進行網(wǎng)格化，周圍四個點氣象數(shù)據(jù)由數(shù)值氣象預(yù)報得到，中間一點可由周圍四點插值得到。圖1為獲取任意點氣象學數(shù)據(jù)示意圖。

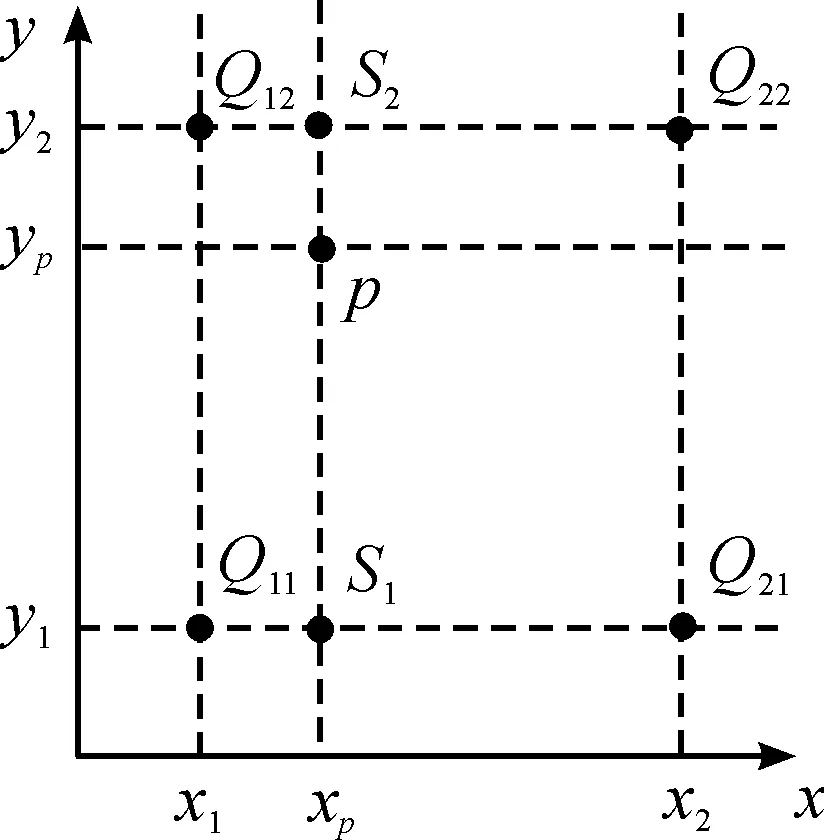
圖1 比例插值示意圖

圖1中，假設(shè)某氣象數(shù)據(jù)的函數(shù)為f，為求得點P(xp,yp)處函數(shù)值，分別假設(shè)函數(shù)在Q11(x1,y1)，Q12(x1,y2)，Q21(x2,y1)，Q22(x2,y2)四點的值，則應(yīng)該首先在x方向進行線性插值，可得到S1(xp,y1)的值和S2(xp,y2)的值。

(1)

(2)

然后在y方向上進行線性插值，得到式(3)，將P點坐標代入式(3)中，到函數(shù)在P點的值為：

(3)

(4)

2 彈道中網(wǎng)格化氣象計算機通報

2.1 計算機通報中各層高度與飛行距離關(guān)系的推導(dǎo)

由于計算機通報中以高度作為依據(jù)對大氣進行分層。網(wǎng)格化氣象計算機通報編制過程中，關(guān)鍵是提取彈丸經(jīng)過區(qū)域不同高度的氣象條件。因此建立彈道區(qū)域內(nèi)高度與水平距離的關(guān)系是解決問題的重點。彈道區(qū)域內(nèi)所處的實際氣象條件和彈丸發(fā)射條件不盡相同，造成了彈道曲線高度與水平飛行距離之間并不是線性關(guān)系。此外彈丸實時飛行中由于水平方向和豎直方向上所受的力不同，速度分量也不相同，飛行高度與位置隨時間變化。為了獲取通用的計算機通報編制方法，就需要對彈丸飛行過程進行簡化。假設(shè)彈丸在真空中飛行，圖2為彈丸飛行的軌跡，其中O點為射擊點，A點為彈道頂點，B為彈道頂點對應(yīng)地面的垂點，C點為彈丸落點。v為速度，θ為射角。

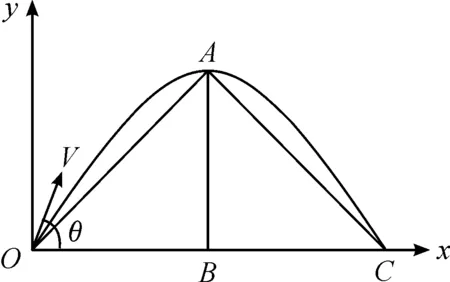
圖2 彈丸飛行軌跡

彈丸飛行最大高度Y為：

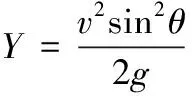
(5)

水平最大距離X為：

(6)

彈道高度與飛行距離之比為：

(7)

空間區(qū)域內(nèi)高度與水平對應(yīng)關(guān)系為：

(8)

式(5)～(8)中，v為初速；θ為射角；g為重力加速度。

2.2 網(wǎng)格化氣象計算機通報中數(shù)據(jù)處理方法

計算機氣象通報較彈道通報不同，每層的劃分并不是均勻的，且與實際測量的氣象雷達或探空氣球所得每層高度不同，這就要求根據(jù)測得的0、200、400、800等各層氣象條件換算成計算機通報所需的不同高度層的氣象。表1 計算機通報分層對照表如表1所示。

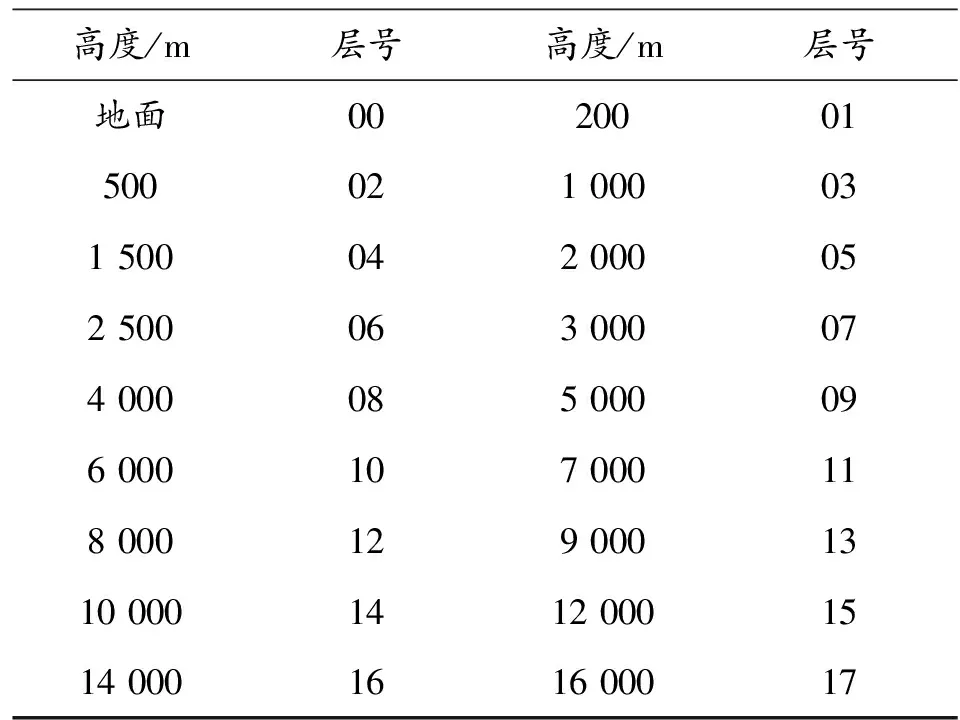
表1 計算機通報分層對照表

由式(8)可知，真空條件下，彈丸飛行高度與水平距離的對應(yīng)關(guān)系與射角有關(guān)。

將彈道分為上升段(圖2中OA段)和下降段(圖2中AC段)，根據(jù)不同射角編寫反映氣象水平變化的計算機通報。以45°射角為例，各層氣象條件換算成計算機通報所需的不同高度層的氣象。網(wǎng)格化氣象數(shù)據(jù)計算機通報的編制過程是：上升段，以炮射點為起點，方向朝向目標。層號00的0 m高為炮射點位置氣象數(shù)據(jù)；層號01的200 m高氣象數(shù)據(jù)對應(yīng)400 m位置處的氣象數(shù)據(jù)；對應(yīng)層號02的500 m高氣象數(shù)據(jù)對應(yīng)1 000 m位置處的氣象數(shù)據(jù)。依次類推，得到上升段計算機通報。下降段，以彈道中點為起點，方向朝向目標。各層數(shù)據(jù)提取方法與上升段相同。

3 仿真驗證

解彈道方程過程中，計算機根據(jù)積分的步長，在氣象通報中實時查取相應(yīng)高度的氣象諸元，并將真實的氣象諸元采用點插值代入非標準條件下彈體運動數(shù)學模型進行積分。根據(jù)虛溫和風的分布規(guī)律，對虛溫在進行線性插值，風的分布有很大的隨機性，對風采用拋物線插值。

以2018年10月25日09時內(nèi)蒙古某地的氣象數(shù)據(jù)為例，分別利用探空氣象測得的氣象數(shù)據(jù)和網(wǎng)格化氣象數(shù)據(jù)進行彈道仿真。探究網(wǎng)格化氣象數(shù)據(jù)計算機通報與探空氣象測量的氣象數(shù)據(jù)對射程和側(cè)偏的影響。仿真過程中假彈箭運動期間的攻角為零；彈箭的外形和質(zhì)量分布關(guān)于縱軸均勻?qū)ΨQ；地表為平面，重力加速度為常數(shù)g，方向鉛直向下；科氏加速度為零。并以初速v=800 m/s，射角θ=35°和θ=50°進行彈道仿真，仿真結(jié)果如圖3～圖8所示、表2～表3所示，其中數(shù)據(jù)1代表探空氣球的數(shù)據(jù)，數(shù)據(jù)2代表網(wǎng)格化氣象數(shù)據(jù)。

圖3 θ=35°時不同計算機通報彈丸軌跡圖

圖4 θ=35°時不同計算機通報射程與射高

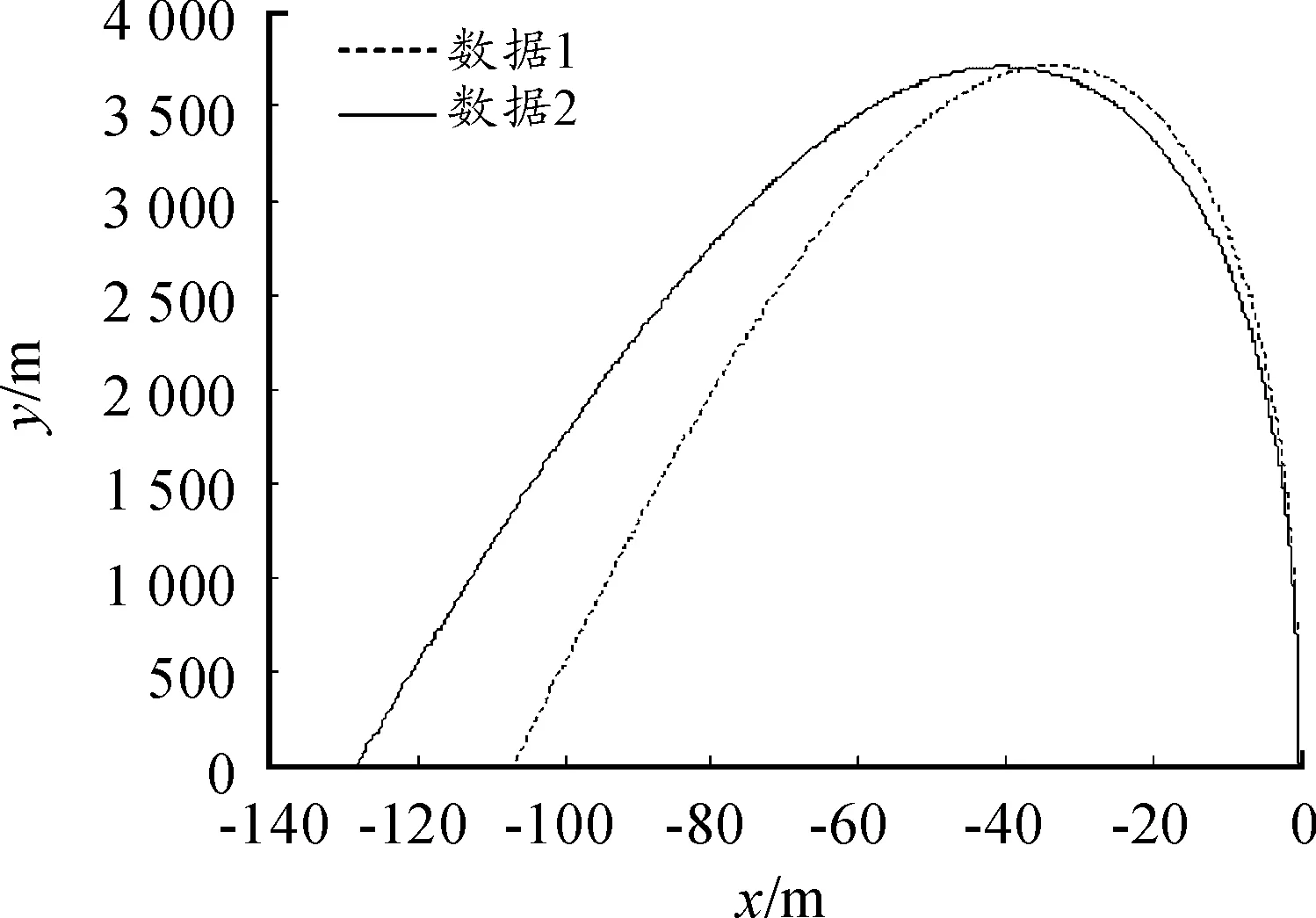
圖5 θ=35°時不同計算機通報側(cè)偏與射高

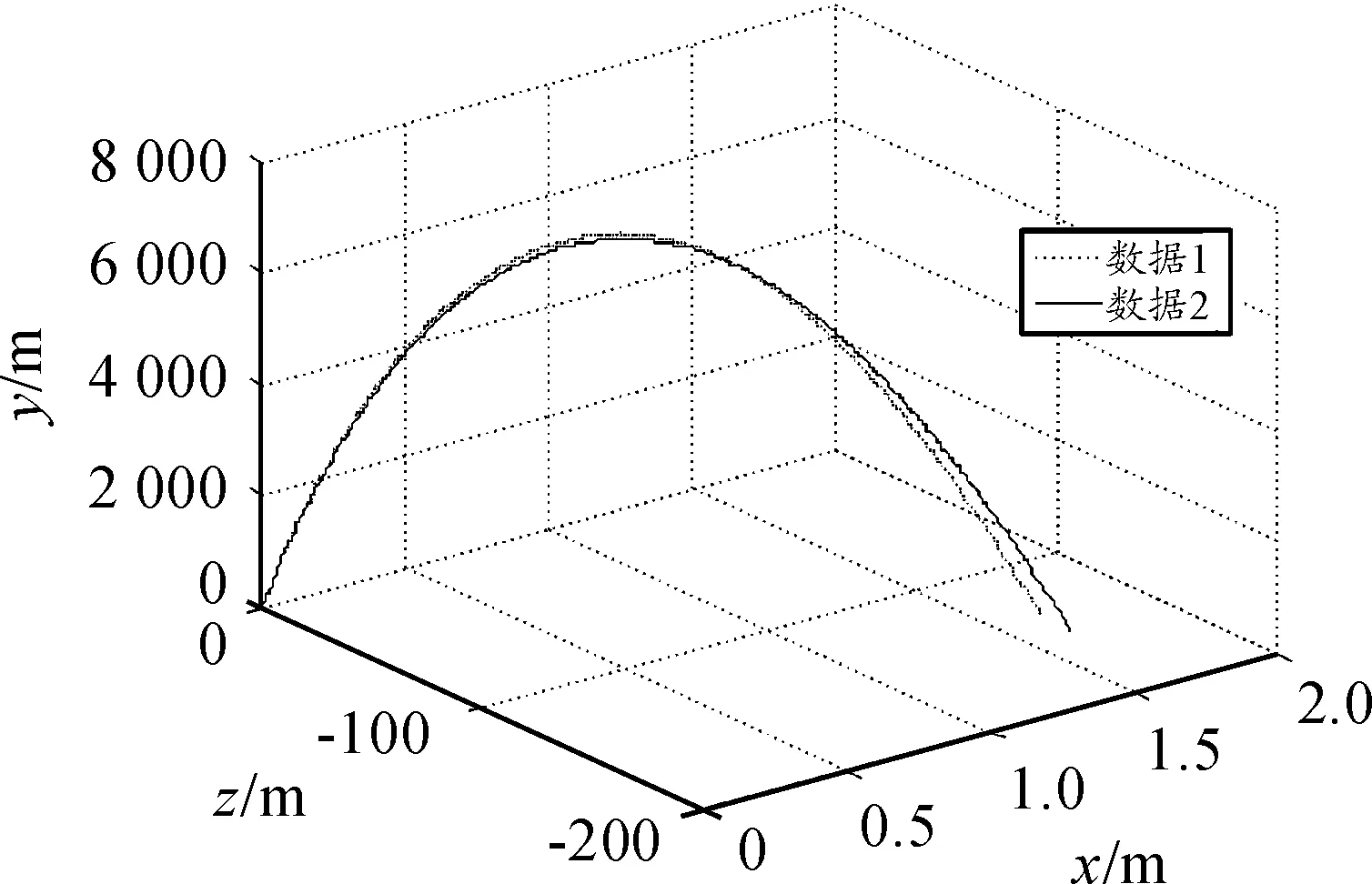
圖6 θ=50°時不同計算機通報彈丸軌跡圖

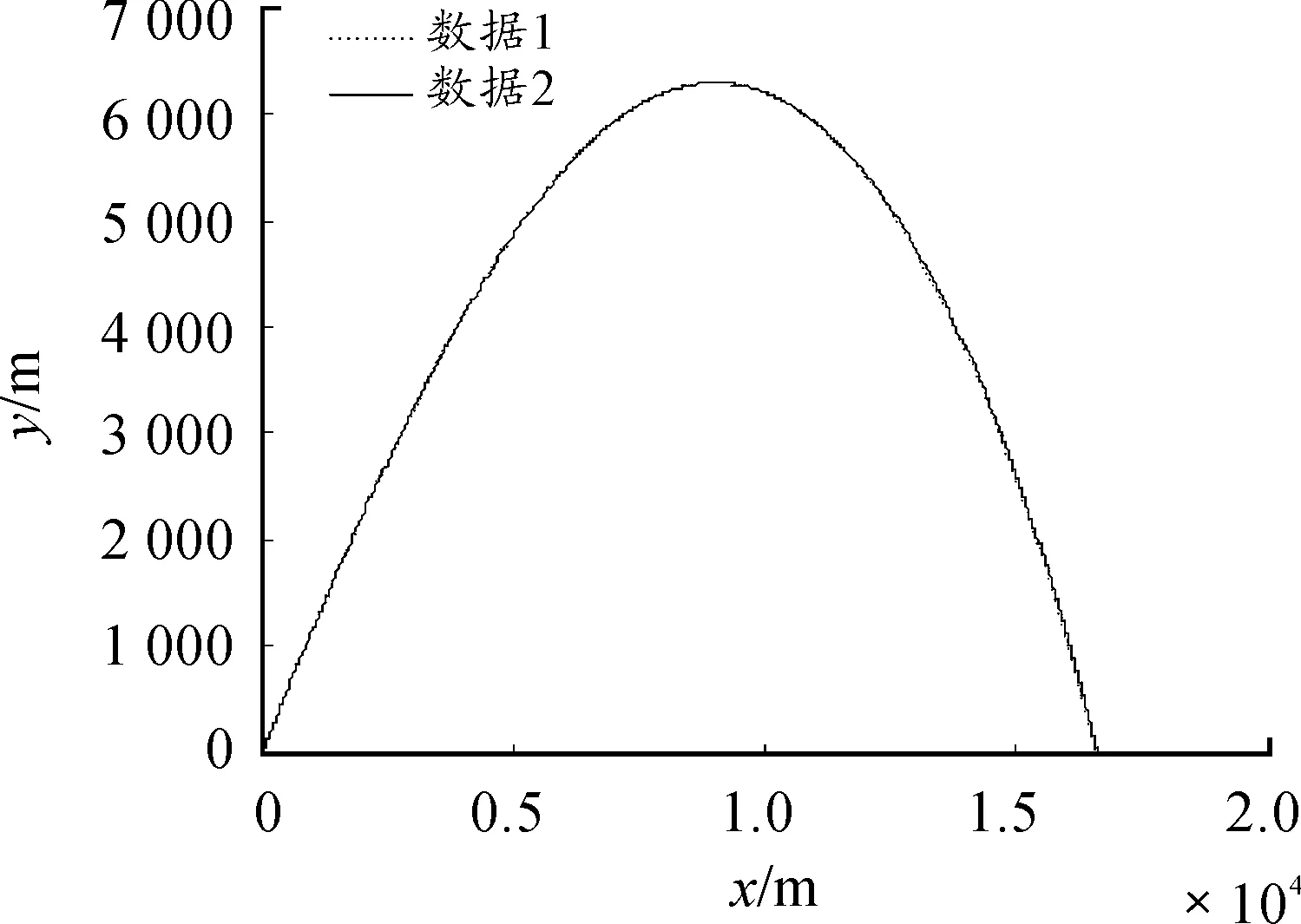
圖7 θ=50°時不同計算機通報射程與射高

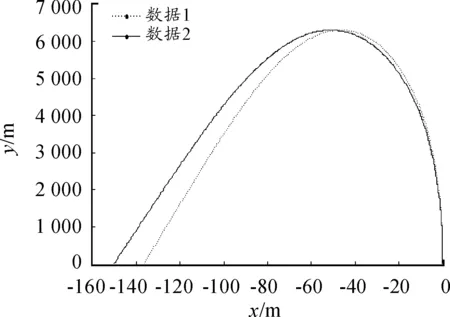
圖8 θ=50°時不同計算機通報側(cè)偏與射高

實際作戰(zhàn)中，由于射擊時間與探空氣球測量時間相比存在滯后，造成數(shù)據(jù)不可靠。但是仿真環(huán)境中，可實現(xiàn)獲取數(shù)據(jù)時刻馬上射擊，誤差較小，可作為對比標準。圖3～圖5分別對應(yīng)35°射角彈丸軌跡圖和射程、偏差隨彈道高度變化圖。以θ=35°射角射擊時，比較不同計算機通報下射擊諸元，僅使用射擊點氣象數(shù)據(jù)的計算機通報條件下彈丸射程、側(cè)偏、彈道高分別為15 687 m、-102.9 m、3 713.2 m。使用整個彈道區(qū)域氣象數(shù)據(jù)的計算機通報條件下彈丸射程、側(cè)偏、彈道高分別為15 837 m、-131.7 m、3 715.1 m。分別變化了150 m、28.8 m、1.9 m，變化相對較小，說明以35°射角射擊時，網(wǎng)格化氣象數(shù)據(jù)具有較高的準確度。

當θ=50°的射角射擊時，僅使用射擊點氣象數(shù)據(jù)的計算機通報條件下彈丸射程、側(cè)偏、彈道高分別為16 601 m、-130.5 m、6 296.7 m。使用整個彈道區(qū)域氣象數(shù)據(jù)的計算機通報條件下彈丸射程、側(cè)偏、彈道高分別為16 731 m、-152.2 m、6 299.4 m。分別變化了130 m、21.7 m、2.7 m，變化相對較小，說明以50°射角射擊時，網(wǎng)格化氣象數(shù)據(jù)具有較高的準確度。

表2 θ=35°不同計算機通報射擊諸元數(shù)據(jù)

表3 θ=50°不同計算機通報射擊諸元數(shù)據(jù)表

4 結(jié)論

本文針對彈道區(qū)域內(nèi)多組氣象數(shù)據(jù)的使用方法不完善的問題，通過簡化彈丸飛行過程，建立了彈丸飛行高度與飛行距離之間的關(guān)系，根據(jù)彈丸飛行高度所對應(yīng)的位置提供相對應(yīng)的氣象數(shù)據(jù)。分別以35°和50°射角進行射擊，比較了傳統(tǒng)計算機通報和網(wǎng)格化計算機通報對彈丸射程和側(cè)偏影響的差異，表明網(wǎng)格化氣象數(shù)據(jù)具有較高的精度，可為后續(xù)彈道區(qū)域內(nèi)多組氣象的應(yīng)用提供借鑒。