帶尾翼射彈跨音速運動過程超空泡流研究

王 瑞， 黨建軍， 姚 忠， 祁曉斌

（1. 西北工業(yè)大學 航海學院， 西安710072； 2. 西北機電工程研究所， 陜西 咸陽712099）

0 引 言

超空泡射彈技術指射彈在水下高速航行時，其表面會形成一層包裹彈身的氣泡[1]，它的存在可以大幅減小航行阻力，極大地提高了水下航行速度以及終點存速，從而有效地提高了射彈對水下目標毀傷效率[2-3]。 為了提高射彈終點存速，運用火炮發(fā)射系統(tǒng)，基于設計優(yōu)良的超空泡射彈在水下以超音速航行，在阻力作用下將經歷由超音速到亞音速的跨音速運動過程[4]。

射彈在水下以音速航行時，在其頭部駐點區(qū)域的液體呈現明顯的壓縮性[5]，流場發(fā)生劇烈的自然空化現象，并且會出現激波現象，而一旦尾翼出現沾濕區(qū)域，亦會受到強烈激波作用。 Vlasenko 等[6]對亞聲速及接近聲速的超空泡射彈進行試驗，發(fā)現了液體可壓縮性對流場有顯著的影響。 Hrubes 等[7]通過高速攝影技術研究了超空泡射彈水中階段的空泡發(fā)展過程、彈體姿態(tài)以及弓形激波等。易文俊等[8-9]開展了帶尾翼高速射彈超空泡減阻試驗與數值模擬， 分析了尾翼對超空泡及其多相流場特性的影響規(guī)律。趙成功等[10]研究分析了不帶尾翼和帶正交分布的三角形尾翼的射彈模型的水下超空泡流形態(tài)和阻力。 從國內外了解到的文獻信息來看，考慮帶尾翼射彈在跨音速過程中空化流場規(guī)律和射彈流體動力特性的相關研究較少。

本文基于FLUENT 軟件，考慮液體的可壓縮性和空化效應，結合SST 湍流模型，通過求解汽水混合物的RANS 方程，建立了帶尾翼射彈水下高速航行的計算模型，開展了馬赫數Ma 為0.7～1.05（對應速度范圍在1 000～1 500m/s）范圍內射彈的空泡特性和流體動力特性的研究，為下一步開展超空泡射彈外形結構優(yōu)化以及流體動力布局設計研究奠定了基礎。

1 數值計算方法

1.1 控制方程

控制方程由質量守恒定律獲得的連續(xù)方程和由動量守恒定律所得的動量方程，分別如下式所示。

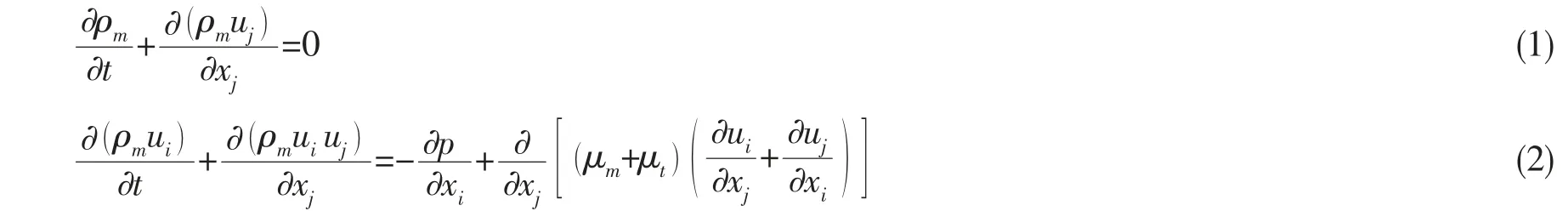
1.2 湍流模型

文中采用的是基于Baseline k-ω 的添加渦黏度限制方程而得到的SST 湍流模型， 該模型對于逆壓梯度下的流動分離問題有更精確的預測。 Baseline k-ω 湍流模型的控制方程為[11]:

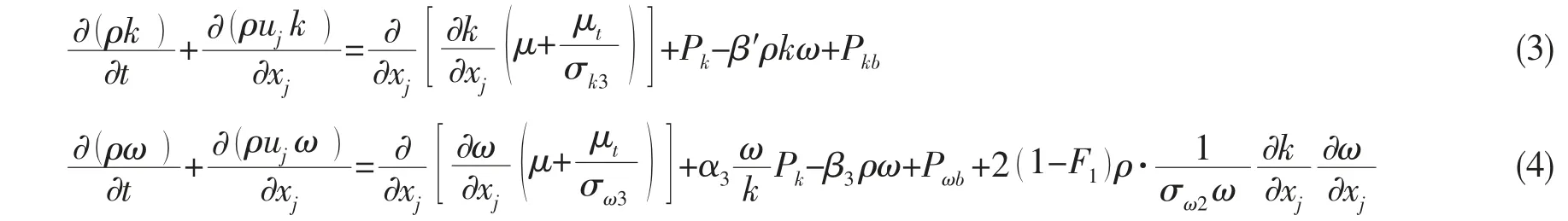
SST 湍流模型中添加的渦黏度限制方程為

式中: μ 為流體的黏性系數； μt為湍流黏度；νt=μt/ρ；F1、F2分別為混合函數；Pk、Pkb分別為湍動能中由黏性力產生的部分和由浮力產生的部分；常數β′=0.09；S 為應變率的不變測度。

1.3 空化模型

描述空化流動的重要參數為空化數，表示為

式中:p∞為無窮遠處流場壓力；pc為當前溫度下水的飽和蒸汽壓力；ρ/2 為流場的參考動壓力。 空化數表征流場空化程度的強弱，空化數越小說明流場的空化越明顯。

采用基于Rayleigh-Plesset 方程的氣泡流動模型來模擬流場的空泡流動。 發(fā)生空化時，流場中水和水蒸汽的質量轉化輸運方程為:

式中，Γi為進入第i 相的單位體積質量源。

簡化的Rayleigh-Plesset 方程為

式中:p 為氣泡周圍無擾動的流場壓強；RB表示氣泡的半徑；pc為水的飽和蒸汽壓。

氣體體積分數為

式中:NB為單位體積內的氣泡數量。

氣泡產生和凝結的質量轉換為:

式中，F 為經驗常數。

1.4 Tait 方程

模擬射彈跨聲速運動，必須考慮液體的可壓縮性。 Tait 方程通過采用非線性回歸的方法，對能夠反應壓力-速度-溫度三者關系的試驗數據進行擬合，從而得到液體狀態(tài)方程[12]。 為了簡化模型，建模過程中不考慮流場溫度變化對物性的影響，采用忽略溫度修正項的簡化Tait 方程。簡化Tait 液體狀態(tài)方程為:

聲速是介質中微波壓力擾動的傳播速度，計算公式為

式中:p0為參考壓力，取101 325 Pa；ρ0為參考壓力下的液體密度，取1 000 kg/m3；K0為參考壓力下的液體體積彈性模量，取2.2 GPa；n 為密度指數，取7.15；p 為當前壓力（Pa）；ρ 為當前壓力下的液體密度（kg/m3）；K 為當前壓力下的液體體積彈性模量（Pa）；c 為水中聲速，約為1 430 m/s。

2 射彈模型與計算域網格劃分

本文研究所用的射彈模型外形如圖1 所示，由空化器、圓錐段、圓柱段以及尾翼四部分組成,其中共6 片尾翼，沿彈體尾部周向均布。 射彈外形主要特征參數參考文獻[9]，彈體具體參數見表1。

圖1 射彈模型Fig.1 The model of projectile

計算域及邊界條件的設置如圖2 所示。 考慮到計算模型和流場的對稱性，計算區(qū)域選取半模計算，定義射彈頭部中心位置為坐標軸原點，入口邊界距離射彈頭部取為3L，圓柱域半徑為50D，彈體尾部距離出口邊界取15L。 計算域入口采用壓力入口邊界條件，外側及出口采用壓力出口邊界條件，設置1 m 水深環(huán)境條件。

表1 射彈外形尺寸Tab.1 Size of the projectile model

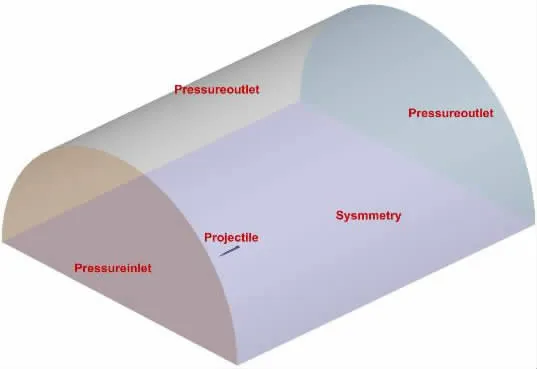
圖2 計算域及邊界條件設置Fig.2 The computational domain and boundary conditions

計算域及彈體附近的網格劃分如圖3 所示。采用的計算網格均為結構六面體網格劃分，可以提高計算效率；對模型壁面附近參數梯度變化較大的區(qū)域進行了局部加密， 模型表面最小網格尺度為0.1 mm，尾翼區(qū)域進行加密處理。 計算過程中進行了網格無關性驗證，最終確定的網格數量約為246 萬。

3 數值模擬結果與分析

圖3 計算域的網格劃分Fig.3 Mesh of the computaional domain

3.1 數值模型校驗

基于建立的數值模擬方法，采用可壓縮液體作為介質，針對文獻中的射彈外形和運動參數，基于建立的數值仿真模型對試驗過程進行數值模擬，并將計算結果與試驗數據進行對比。 空泡輪廓的數值結果與試驗結果對比如圖4 所示。可以看出，數值模擬所得超空泡輪廓與文獻提供的試驗數據基本吻合。 亦證明了本文建立的考慮可壓縮的數值模擬方法是合理可信的。

3.2 尾翼射彈超空化流場結構分析

基于建立的數值模型，計算超空泡射彈在水中以馬赫數為0.7～1.05 的航行速度下的超空化流場。

圖5 給出了速度為1Ma 時的射彈彈身段和尾翼段的流線圖。可以看到射彈頭部空穴內部的渦流，尤其射彈尾部的流場受到尾翼的擾動，并在彈尾形成渦對，尾渦的速度較低并且強度隨著速度增大而加大。 這些渦流存在三維效應，這里展示的為穿過XY 平面的流線。

Fig.4 Comparsion of supercavitation outlines drawn by different methods

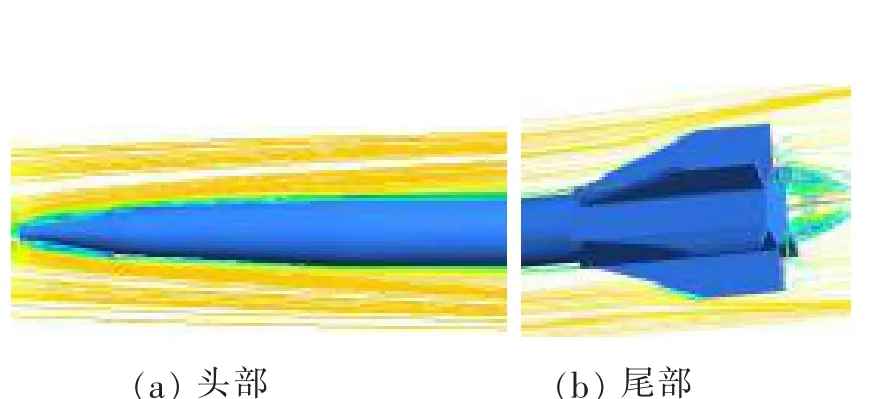
圖5 Ma=1 時的流場流線Fig.5 Streamlines pattern (Ma=1)

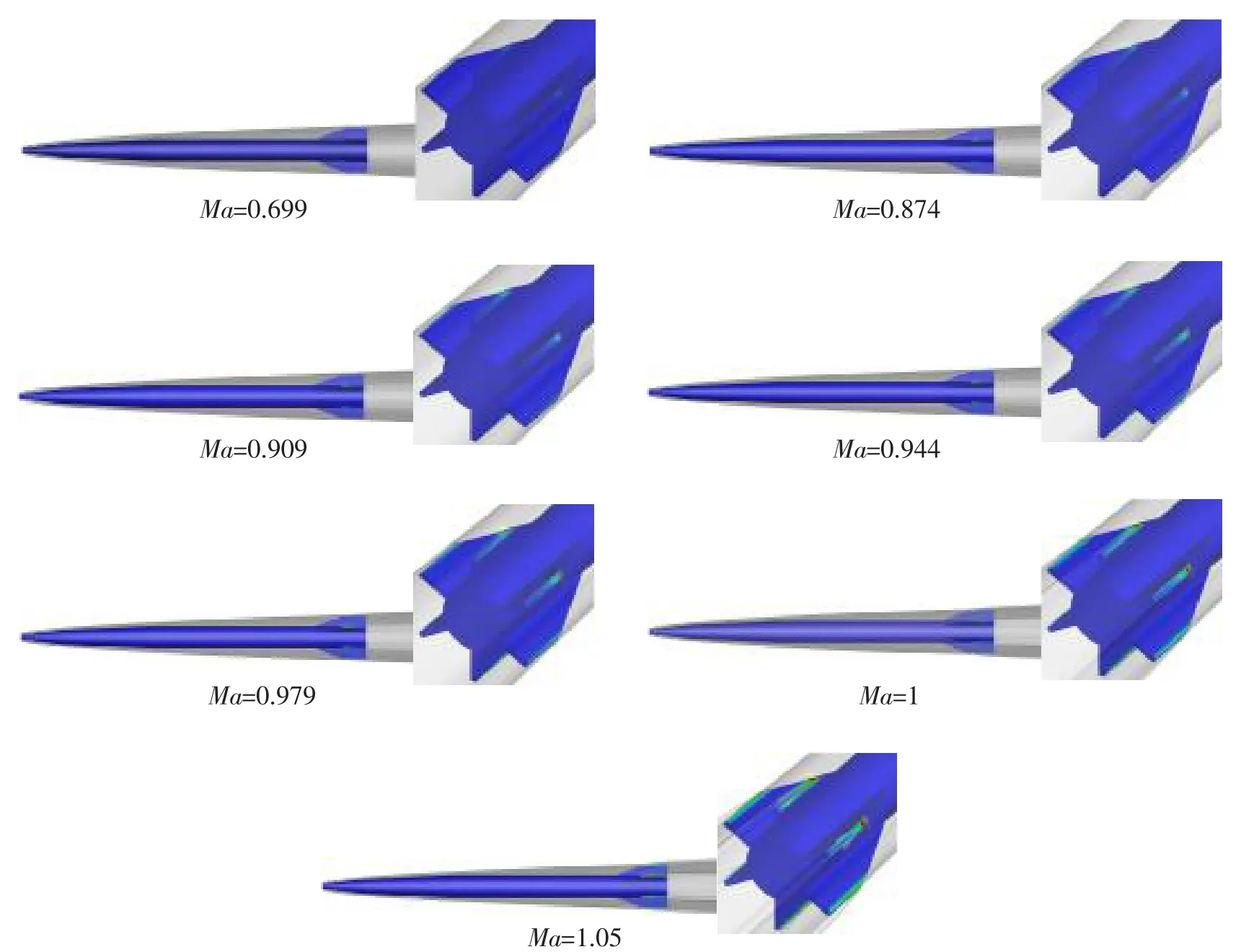
圖6 不同計算工況下的空泡形態(tài)Fig.6 The cavity morphology at different conditions

圖6 給出了不同馬赫數下的三維空泡形態(tài)變化。圖7 給出了縱對稱面上空泡輪廓曲線對比圖，并進行了無量綱化處理，Dn 為比例因子。 結合圖6 和圖7 可以看出，隨著馬赫數的增大，彈身段空泡完全包覆，但是在彈身附近空泡徑向尺度上逐漸變小，且越貼近彈身呈現明顯的壓縮性；空泡對射彈的包覆狀態(tài)與馬赫數的變化有著密切的聯系，射彈被空泡完全包裹時，隨著馬赫數的增大，尾翼翼尖處亦會出現高壓區(qū)，這是由于空泡內充滿蒸氣，受到空氣動力的作用， 此時的力學特性較弱， 而在Ma＞0.94 時， 空泡輪廓線開始與尾翼邊緣接觸，尾翼出現沾濕，沾濕尾翼的部分使得空泡出現二次空化，此時尾翼的沾濕區(qū)域會產生高壓區(qū)，此時空泡表面不再與彈身段一致，出現光滑帶狀壁面；且由于尾翼的存在，當Ma＞0.94 時，尾翼之間的空泡面被壓縮，尾翼沾濕，空泡縱剖面的形狀不再成橢圓狀，而且馬赫數越大，壓縮程度越大。

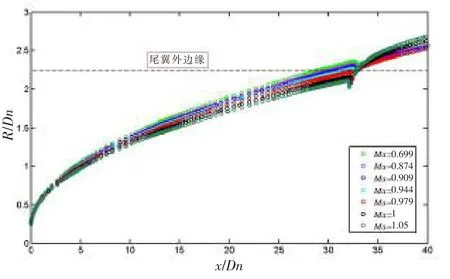
圖7 空泡截面輪廓對比Fig.7 Comparisons of profiles of cavity cross section

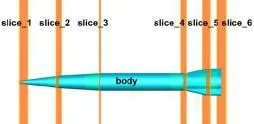
圖8 彈身截面位置Fig.8 Section position of body

通過獲取射彈各個位置切片處的空泡輪廓，來量化了解不同馬赫數下射彈空泡形態(tài)受可壓縮流場作用的影響效應。 圖8 給出了彈身切片位置，分別對彈身的空化器段、圓錐段、圓柱段、尾翼斜面、尾翼平臺等位置進行切片。

圖9 給出了在不同馬赫數下，1/3 彈體模型各個切片位置的空泡形態(tài)。其中，對空泡半徑R 進行無量綱化處理（Ry,z/R），R 為各個切片位置處的彈體半徑。 可以看出:Ma=0.699 和0.874 時，對比彈身同等切片位置的空泡相對尺度基本沒有變化，受到的壓縮效應較小，而錐段處的空泡相對厚度較小，進行錐段優(yōu)化設計時需要重點關注；Ma=1.05 時， 彈體各個切片位置的空泡相對尺度壓縮量明顯，在slice-4 處的空泡相對尺度變化量反而要比在slice-1 處的大。 這可能是由于尾翼的存在，產生的反射激波抑制其空泡的發(fā)展，在slice-5 處，出現尾翼沾濕。

圖9 彈體切片空泡輪廓對比Fig.9 Comparision of cavity profiles in body slices

3.3 射彈阻力特性分析

射彈阻力系數如（15）式所示:

其中:F 為總阻力；V 為來流的速度；S 為射彈特性面積，本文中取射彈空化器的橫截面積。

圖10 給出了跨音速速度區(qū)間內射彈阻力系數變化規(guī)律。 可以看出，在不考慮壓縮性以及通過經驗公式計算獲得射彈的阻力系數近乎為恒定值， 主要是因為未考慮壓縮性以及射彈出現沾濕帶來的影響，不再適用于描述射彈在跨音速運動下的阻力特性；當射彈完全被超空泡包裹時，此時的壓縮性主要體現在對空化器的影響，使得阻力系數增大，其增加量約為不可壓縮量值的8%～9%，且在馬赫數為0.699～0.944 范圍內呈線性遞增；射彈在音速附近運動時，由于流場壓縮性增強，尾翼出現沾濕，尾翼受到強烈的沖擊載荷，使得射彈的阻力系數出現突變，呈現明顯的非線性特性。

圖11 統(tǒng)計了在跨音速運動區(qū)間馬赫數為0.7～1.05 范圍內彈體與尾翼阻力分布圖。

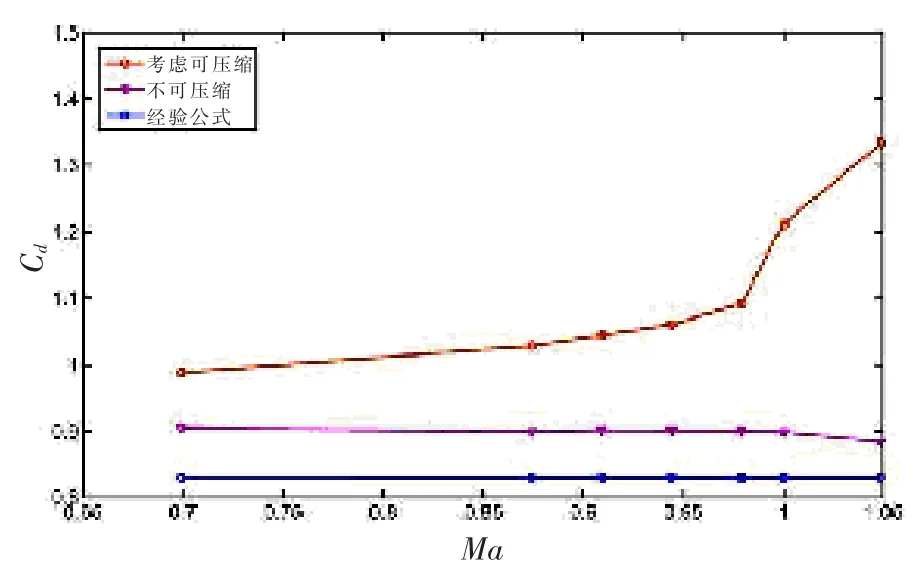
圖10 跨音速運動過程中射彈阻力特性Fig.10 Resitance characteristics of projectiles’transonic motion

圖11 彈體與尾翼阻力分布圖Fig.11 Drag distribution of body and wing

由圖11 可知，隨著速度的增加，彈體阻力逐步增大，Ma＜0.944 時尾翼阻力較小，結合圖5，此時射彈完全處于空泡的包裹， 產生的阻力緣于蒸汽相，其量值較小。 隨著速度接近音速，尾翼阻力占比迅速增加，亦可以解釋圖10 中，射彈阻力系數在接近音速時出現陡增現象的原因。

圖12 給出了射彈在不同速度下彈體與尾翼最大壓力峰值的變化規(guī)律。

從圖12 可知， 射彈受到的最大壓力出現在頭部空化器，Ma＜0.944 時，尾翼處的壓力較小，而當馬赫數超過0.944 后，尾翼處的壓力急劇增大，彈身總的最大壓力隨著速度的增加而增大， 結合圖11 可以解釋阻力系數產生突變的原因，主要原因是尾翼出現沾濕。 因此掌握跨音速運動時彈體的受力特性對選擇彈體材料和優(yōu)化尾翼結構有重要的指導意義。

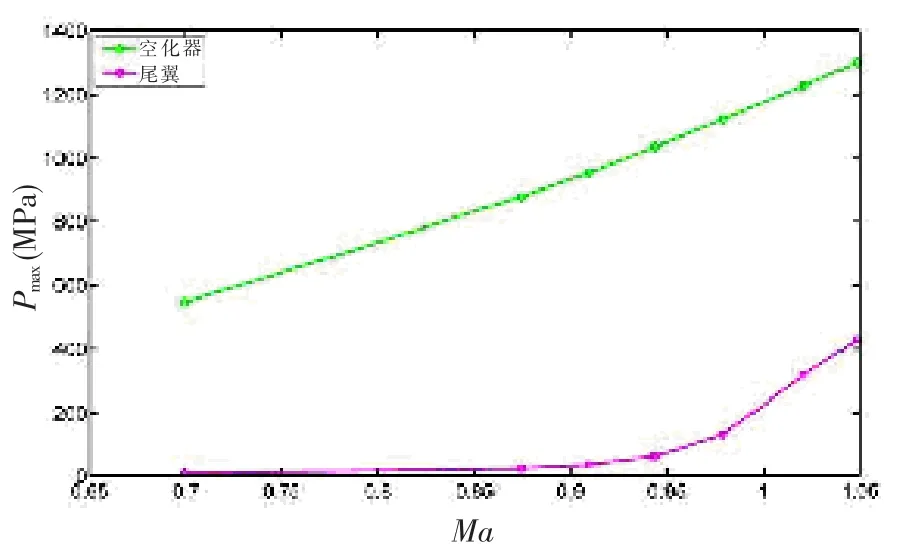
圖12 彈體與尾翼最大壓力變化規(guī)律Fig.12 Maximum pressure variation of body and wing

4 結 論

本文通過數值模擬對帶尾翼射彈在跨音速0.7～1.05 運動區(qū)間的超空泡流特性和阻力特性進行了研究。 通過分析不同工況下流場的流動參數，揭示了射彈航行速度對空泡和阻力特性的影響機理。 主要結論如下:

（1） 在跨音速運動區(qū)間內，射彈尾部出現強烈的渦流現象，使得空化流場更加復雜，射彈彈身段能夠被空泡完全包覆，而尾翼的包覆狀態(tài)隨著越接近音速，越容易出現沾濕，射彈被空泡完全包裹存在臨界狀態(tài)，本文中的研究模型臨界值Ma=0.944。

（2） 尾翼出現沾濕后，沾濕區(qū)域形成高壓區(qū)，抑制空泡的發(fā)展，翼緣發(fā)生二次空化，空泡形態(tài)不再呈橢圓界面，出現凸起外形。

（3） 射彈在跨音速航行過程中，速度越大，其阻力系數越大，在接近音速時，阻力系數出現陡增，尾翼阻力占比增大；尾翼一旦沾濕，會受到巨大的壓力沖擊，其量級可達102MPa，較大的壓力峰值會對尾翼的結構造成影響，乃至影響彈道的穩(wěn)定性。

文中研究結果可以為開展超空泡射彈外形結構優(yōu)化以及流體動力布局設計工作提供指導。