深海立管渦激振動雙穩態現象

李江濤， 吳志強， 王遠岑， 張祥云

（天津大學a. 機械工程學院； b. 天津市非線性動力學與混沌控制重點實驗室， 天津300350）

0 引 言

多穩態現象是非線性系統的重要動力學行為之一。 當系統中存在多穩態時，不同初始條件或擾動，可能導致系統行為趨于不同吸引子，最終振動特征往往有重要區別。 多穩態導致的這種振動行為的不確定性，會對工程結構的設計和運行帶來嚴重危害。

管道渦激振動中結構動力與尾流水動力的相互作用非常復雜， 而且二者的耦合作用具有很強的非線性特征[1]。 其響應是否存在多穩態現象，若存在其有何特點，是一個值得關注的理論和工程問題。

已有小尺度實驗研究表明， 流速增大或減小時管道振動存在遲滯現象， 在遲滯區有多解共存現象，即渦激振動多穩態行為確實存在。 Feng（1968）[2]首先在彈性支撐柱體風洞實驗中發現折合速度約為6 時管道出現遲滯現象，其響應曲線同時包含初始分支（initial branch）和下端分支（lower branch）。Brika、Labeville 等[3]隨后也在風洞中進行了相關的實驗，選用了阻尼比與Feng（1968）[2]不同的空心管道，得到了更大的“鎖頻”區間和兩倍于Feng 實驗結果的滯后區域。 后來，Williamson[4-6]對中等雷諾數的低質量比彈性支撐圓柱體進行了一系列的實驗，發現質量阻尼比m*ζ 不同時，渦激振動系統會出現兩種不同的響應。 大m*ζ 時，系統的響應存在兩個分支:初始激勵分支（initial excitation branch）和下端分支（lower branch），最大振幅出現在初始激勵分支上；小m*ζ 時，系統響應存在三個分支:初始分支（initial branch）、上端分支（upper branch）和下端分支（lower branch），最大振幅出現在上端分支上。系統響應在初始分支與上端分支、上端分支與下端分支之間都發生了跳躍現象，前者屬于遲滯，后者屬于間歇切換。

盡管渦激振動的多穩態現象已被實驗證明，理論分析的研究卻較少有相關的報道，焦點也多在預測模型上。 關于結構渦激振動響應的預測模型有多種，其中尾流振子模型因為其具有較為明確、合理的物理意義以及較好的計算精度，被工程界廣泛采用。 該模型通過相互獨立的方式分別建立圓柱振子運動方程和流體振子運動方程，然后利用它們共同預報流體-彈性系統的動力響應。Hartlen 和Currie[7]在Bishop 和Hasson[8]等人研究的基礎上，首次提出了尾流動力可以使用Van der Pol 方程作為升力系數的控制方程，并且可以與結構的振動方程聯立求解。后來Iwan[9]和Blevins[10]通過研究，給出了用于二維流場彈性支撐剛性圓柱的尾流振子模型。Facchinetti 和Langre[11-12]對前人的工作進行了總結，并且對比了位移、速度、加速度耦合尾流振子模型，認為加速度耦合模型可以更好地模擬結構對流體的作用，但是在預測鎖頻區域寬度時，僅適用于小質量比情況，隨著質量比增大，簡縮速度范圍估計偏于保守。陳偉民和鄭仲欣[1]在前人研究的基礎上，結合并利用速度耦合模型和加速度耦合模型的優點，提出來一種新的非線性耦合模型，且與實驗結果對照較為準確。 關于渦激振動中的多穩態現象，還有人做了一些相關的研究,陳威霖和及春寧等[13]研究了單圓柱渦激振動中的振幅不連續和相位切換現象，結果表明當阻流比小于0.05 后，鎖定區間向更高的折合流速偏移，上端分支和下端分支之間的遲滯環寬度增大近4 倍，并解釋了圓柱升力和位移之間相位差跳躍現象。

本文利用Van der Pol 尾流振子模型描述流體的作用， 選用非光滑平方非線性項描述流體對結構的阻尼作用，采用加速度耦合模型，建立深海立管的渦激振動動力學模型。應用Poincaré 映射方法，研究流速變化引起立管渦激振動行為的分岔現象，從而深入分析流速變化對渦激振動的影響。

1 深海立管渦激振動模型

1.1 立管振動模型

立管頂部通過張緊器與海上平臺相連接，張緊器可以簡化為一個剛度為k 的彈簧。 其作用主要有兩點:一是可以為管道提供一個較大的靜張力從而避免管道產生較大的彎曲；二是可以減小由于平臺的垂直運動產生的縱向應力對立管的影響[14]；立管底端簡化為鉸支連接，模型示意如圖1 所示。

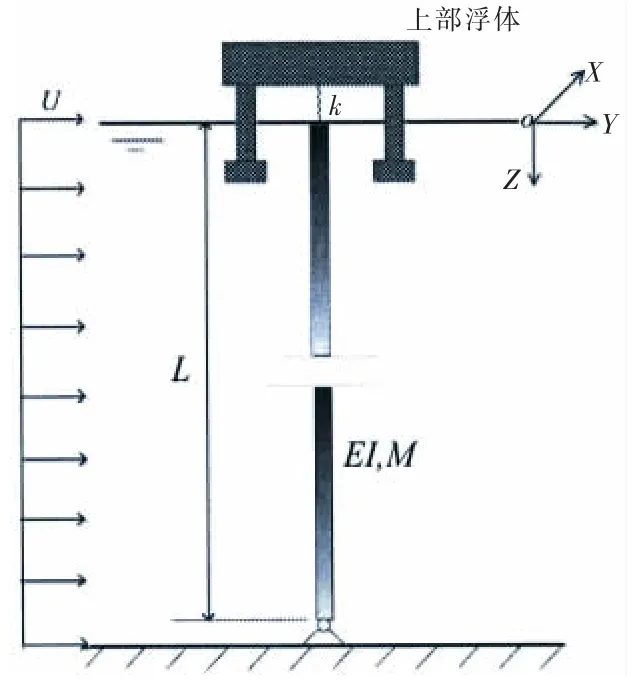
圖1 立管模型示意圖Fig.1 Diagram of the riser model

基于Euler 梁的彎曲振動理論，立管橫向振動的基本方程可表示為

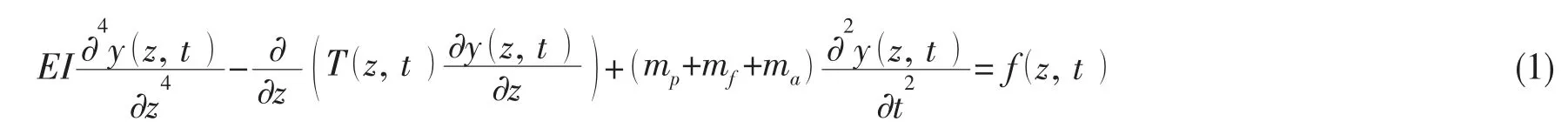
式中:y （z, t ）為立管的橫向位移， 是關于垂向坐標軸z 和時間t 的連續函數；EI 為立管的抗剛度；mp=πρp（D2-d2）/4 為單位長度管道質量，mf=πρfd2/4 為內部流體質量，ma=CaπρwD/4 為管道附加質量，其中ρp、 ρf、 ρw分別為立管材料密度、內部流體密度和海水密度；D、d 分別為立管的內外直徑；Ca為附加質量系數，一般取1； f （z, t ）為立管單位長度上的作用力；T （z, t ）為立管的有效張力，其表達式為

1.2 尾流振子模型

尾流振子模型即不考慮具體的流場結構，而是將流體和其中的振蕩物體視為一個整體系統，把尾流部分看成一個非線性振子，尾流振子的振動引起結構的振動；反過來，結構的振動又對尾流有一個反饋的作用。 本文采用Van der Pol 方程來表示旋渦脫落的振動特性，同時用慣性耦合來表達其與結構運動間的耦合作用。 具體形式如下[11-12]:

式中:η 為流體對結構的瞬時升力系數CL和結構靜態橫向升力系數CL0之比，η=2CL/CL0；Ωf為漩渦脫落的圓頻率，Ωf=2πStU/D，其中U 為水流流速，St為Strouhal 數，本文取St=0.2；A、ε 為經試驗測定的耦合系數，分別取12 和0.3。

流體對立管的作用力包含兩部分: f= fL+ fL′。 其中渦激升力為

阻尼力為

式中CD為流體阻力系數，取1.2。

1.3 流固耦合模型

引入如下無量綱量將方程（1）和（3）進行無量綱化:

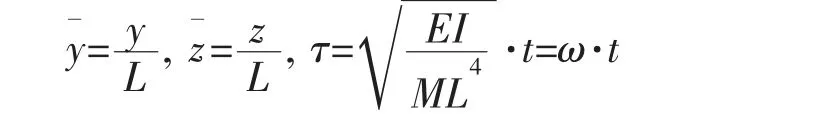
式中，M=mp+mf+ma并對其進行伽遼金離散，假設解有如下形式:

其中離散系統中各系數具體表達式如下所示:

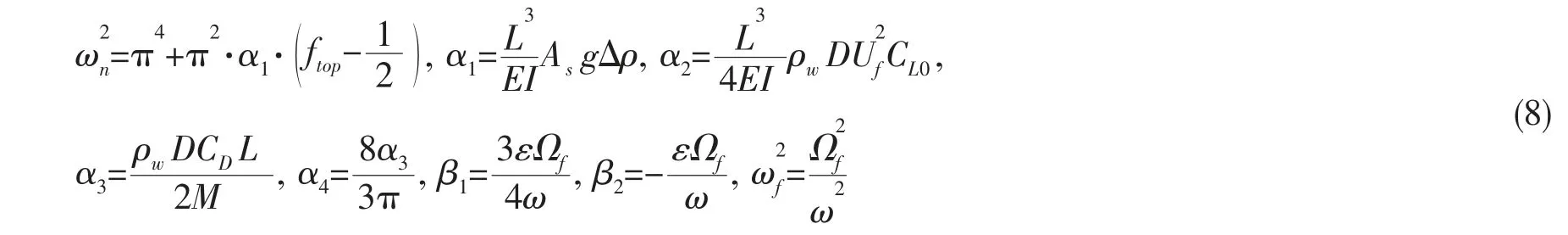
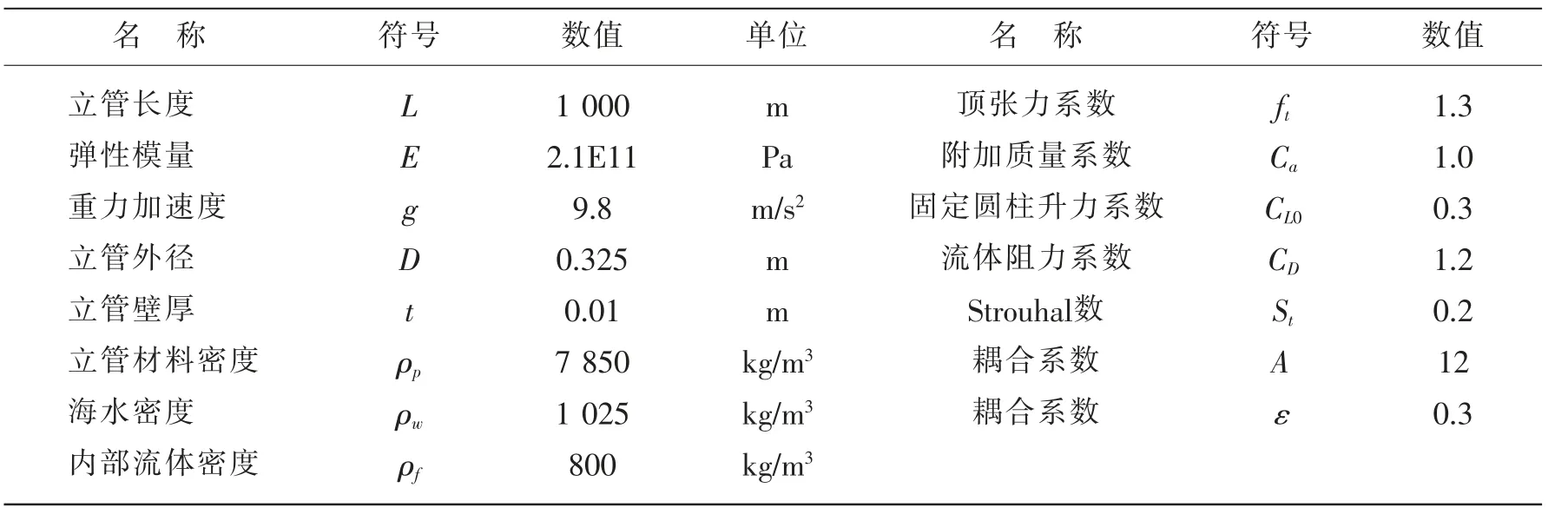
表1 計算模型參數[15]Tab.1 Calculation parameter of model

2 流速變化對系統穩定性影響

因此，分別計算了有阻尼、無阻尼兩種情況下系統特征值隨流速變化的情況見圖2。 無阻尼情況下，特征值隨流速變化，純虛特征值逐漸接近至相等，然后變成兩對虛部相等的復重根，再變為兩對純虛根。 U∈（0.025-0.085 m/s）間屬于耦合顫振，為平衡點不穩定，而其他區間平衡點是中心穩定的；有阻尼時，U 約為0.05 m/s 時，渦激頻率與結構頻率大小交換（臨界值可從虛部顏色變化看出）。 由于始終有一對復根實部大于0，平衡點始終是不穩定的，即立管處于渦激振動狀態。

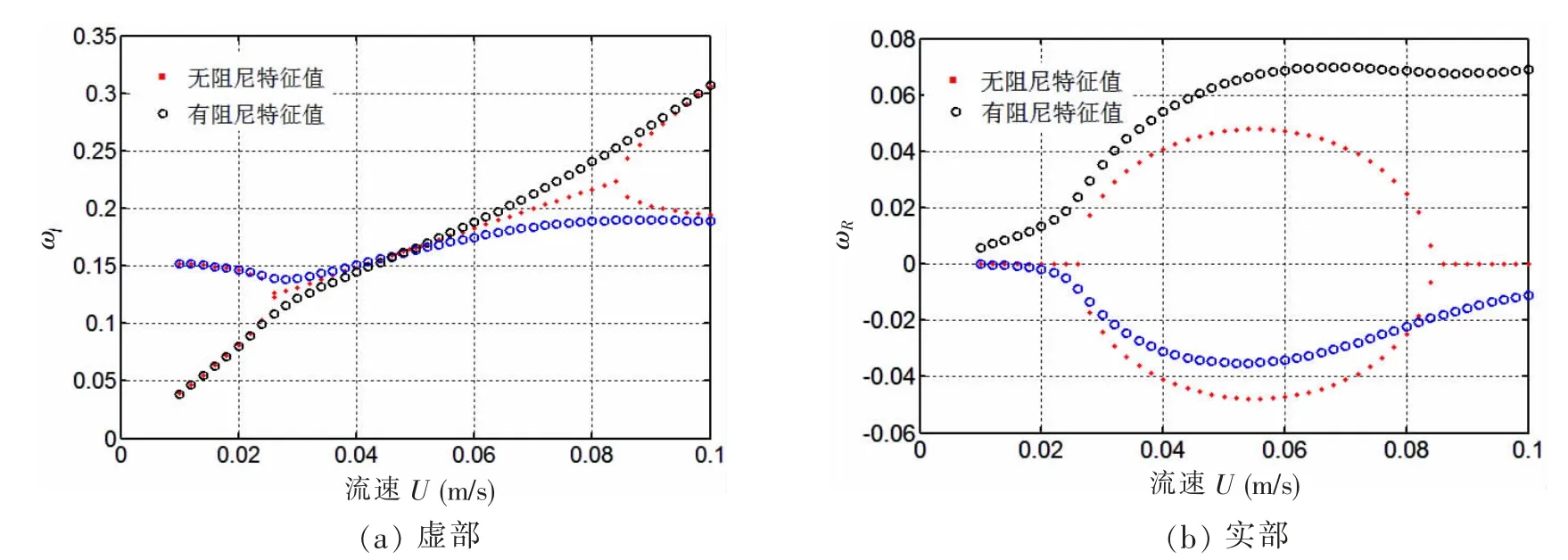
圖2 特征值隨流速變化圖Fig.2 Variation of eigenvalues with flow velocity

3 流速變化對系統行為的影響

復雜非線性系統動力學理論分析通常比較困難， 因而數值方法成為通常采用的手段， 其中Poincaré 映射方法得到較廣泛的應用。 根據Poincaré 截面上點的分布情況，即可對系統響應類型進行判斷。 當系統響應達到穩態以后，若Poincaré 截面上的點數目有限時，對應的響應是周期的；若這些點形成閉環，則對應的運動是概周期的；若這些點在有限區域形成一定形態的吸引子，則對應的運動可能是混沌的。

3.1 流速變化導致的分岔及雙穩態現象

Poincaré 映射方法用于分析參數引起的系統響應行為變化時，可得Poincaré 截面上點隨參數的變化圖，稱為Poincaré 分岔圖。 如果采用參數延拓法，同時獲得參數遞增和遞減的兩個分岔圖，則可從是否存在滯后/跳躍現象來判斷是否存在多穩態現象。 用Poincaré 方法分析系統分岔時，Poincaré 截面選擇有重要影響。 為得到振動幅度隨參數的變化圖，本文選用截面定義為

本節利用Poincaré 映射方法分析水流流速在0.01-0.20 m/s 之間變化時立管振動行為的變化。 圖3 給出了流速遞增、遞減兩種情況下的Poincaré 分岔圖計算結果，而豎直方向的箭頭表示解發生跳躍的方向。（其中“實線箭頭→” 表示正向，“虛線箭頭 ”表示反向）。從圖3 可以看出，增大流速和減小流速時算得的立管振動響應基本一致，立管的振動響應隨著流速的增大呈現出先增大后減小的趨勢，并且出現了渦激振動特有的“鎖頻”現象。當折合速度小于3 時，立管振動響應較小，此時渦激振動對管道的影響較小，尾流和管道之間的相互影響也較小；當折合速度處于4～11 之間時，管道出現較大的振動響應，振幅均大于0.6D，最大可達到1.2D。 此時管道振動頻率接近漩渦脫落頻率并出現了“鎖頻”現象；隨著流速繼續增大，立管振幅也隨之減小。 在“鎖頻”區域兩側，出現了因解跳躍導致的滯后現象。 這與Feng （1968）[2]和Williamson（1996-1999）[4-6]等學者在實驗中發現的現象類似，在滯后區間內有雙穩態現象。

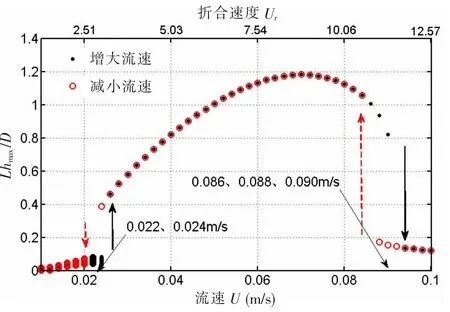
圖3 增大流速和減小流速時立管振動響應對照圖Fig.3 Comparison of riser vibration response with increasing flow velocity and decreasing flow velocity

特別需指出鎖頻解存在范圍U∈（0.024-0.086 m/s）與前文得到的耦合顫振范圍U∈（0.025-0.085 m/s）較為接近，也就是說可用線性分析得到的耦合顫振區來估計渦激共振導致的鎖頻區。這一結論與Langre（2006）[18]所得結論一致。

為了進一步說明這類行為的特點，又分別計算了典型流速下立管振動響應的時間歷程、相圖和頻譜。 在鎖頻區左側，當折合速度為3.02 時，增大和減小流速情況下得到的時間歷程、相圖、頻譜如圖4所示。 從兩圖中可以很明顯地看出在增大流速時，其時間歷程呈現出明顯的“拍頻”現象，屬概周期運動，振動幅值最大值也僅為0.08D，頻譜中含兩種不同的頻率成分；而在減小流速的情況下，其時間歷程呈現出較為規整的正弦圖像，響應振幅達到0.4D，而頻譜中僅含一種頻率成分，接近立管線性固有頻率，屬周期運動。說明當折合速度為2.77-3.02 區間內存在周期運動、概周期運動共存的雙穩態現象。

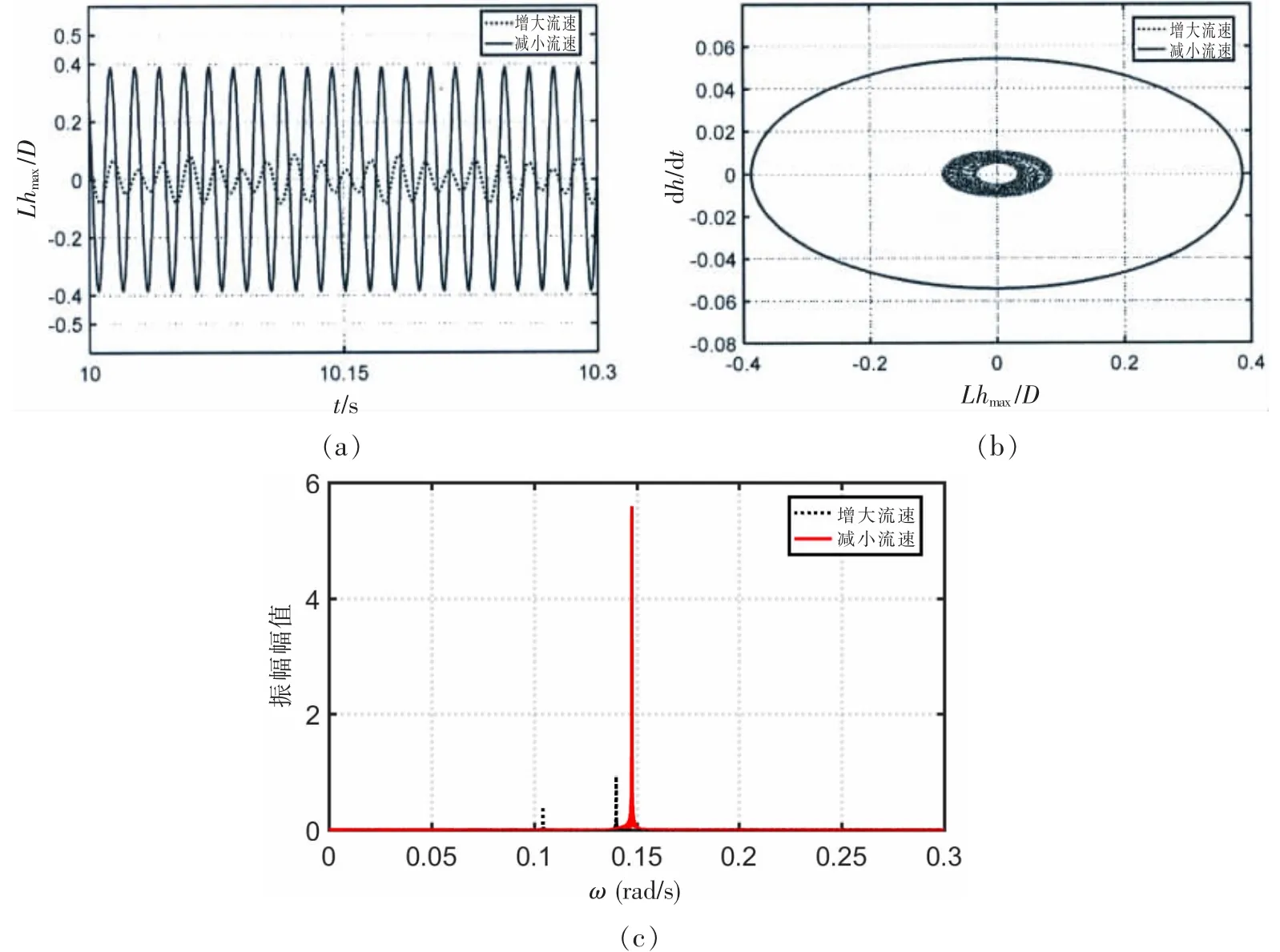
圖4 增大和減小流速時立管的時間歷程圖、相圖和譜圖（折合速度3.02）Fig.4 The history, phase diagram and spectrum of riser with increasing and decreasing flow velocity at a reduced speed of 3.02

在鎖頻區域右側，當折合速度為11.06 時，增大和減小流速情況下的結果如圖5 所示。在該折合速度下，響應的不同主要體現在振動幅值大小和頻譜中主要頻率的不同。 當增大流速時，系統的振動幅值可以達到0.93D 左右，頻譜分析得到的主要頻率為0.186 rad/s；而當減小流速時，系統的振動幅值只有0.17D 左右，頻譜分析得到的主要頻率為0.249 rad/s；顯然，當折合速度為10.81-11.32 區間內雙穩態現象是兩類不同周期運動的共存。

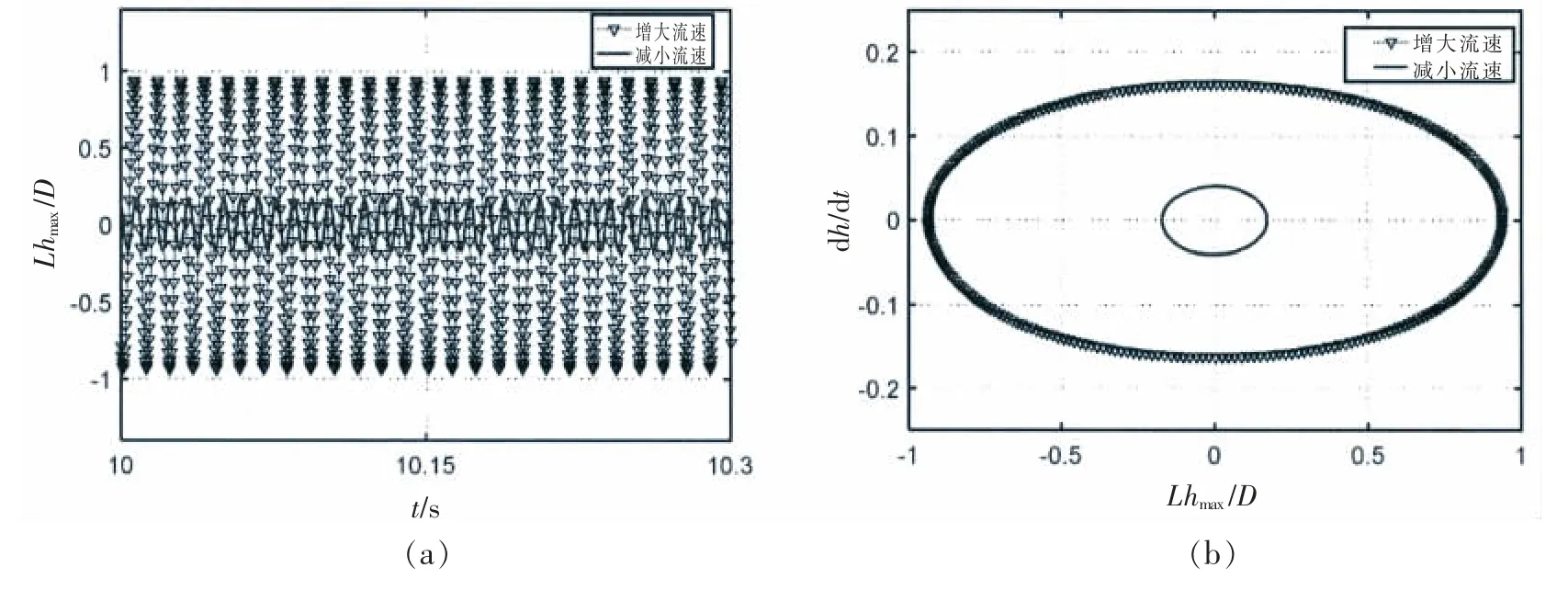
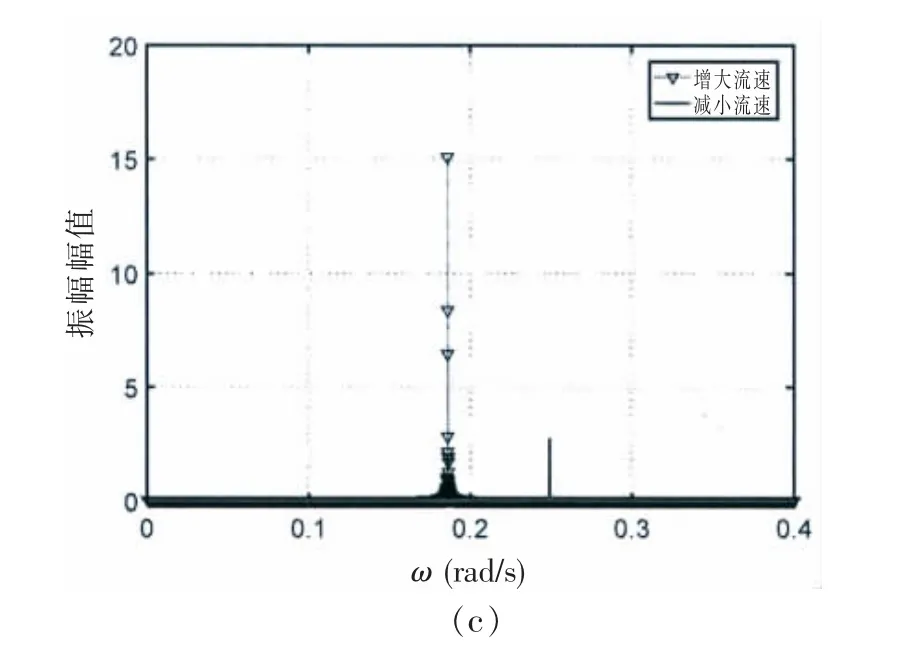
圖5 增大和減小流速時立管的時間歷程圖、相圖和譜圖（折合速度為11.06）Fig.5 The history, phase diagram and spectrum of riser with increasing and decreasing flow velocity at a reduced speed of 11.06

通過具體對各流速下立管振動響應的分析， 可以更清楚地看出立管在這些流速下的振動響應均產生了雙穩態現象。 其差異既有振動形態的不同，也包含振動幅值、頻率的差別。

3.2 響應頻率和相位差變化規律

為了進一步研究立管響應頻率在選取流速范圍內變化規律， 本文分別計算繪制了立管響應頻譜和尾流振子頻譜隨流速變化的三維圖形，如圖6-7 所示。

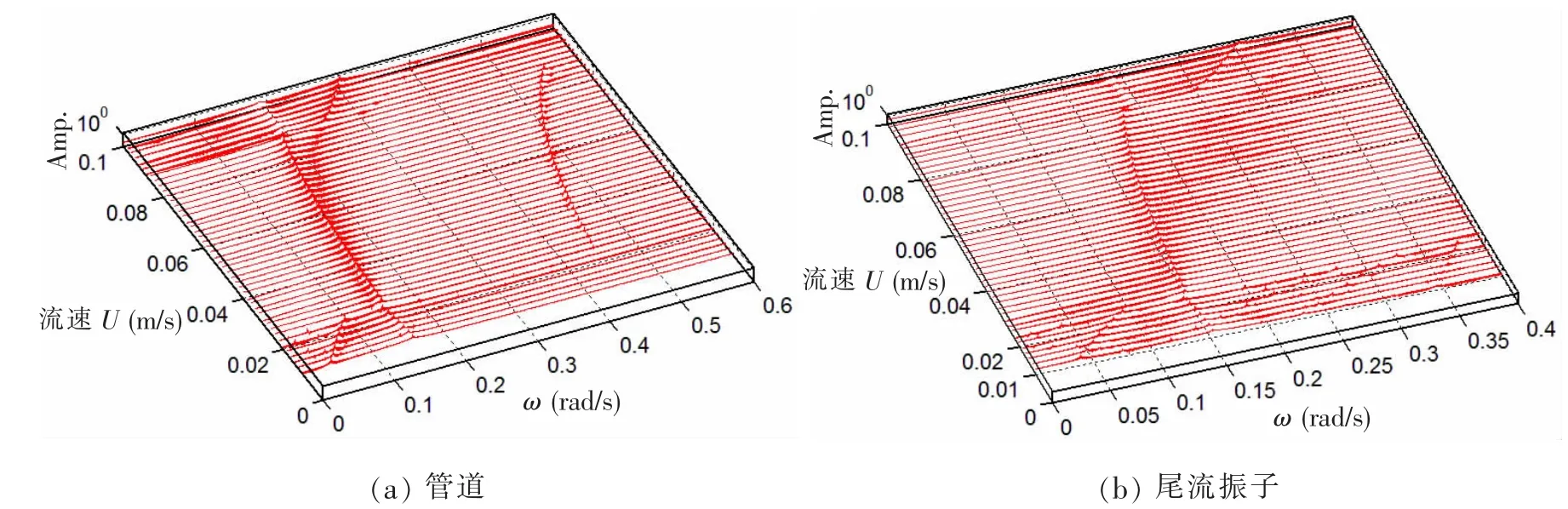
圖6 1 000 m 立管振動響應三維頻譜圖Fig.6 Three-dimensional spectrum of 1 000 m riser’s vibration response

根據譜分析結果提取了主要頻率成分隨流速變化結果見圖7， 為反應響應的本質圖中還給出了有阻尼情況下特征值頻率的結果。

圖6-7 清晰地反映了其振動響應頻率隨流速變化的規律:

（1） 當流速較小時（0.010-0.022 m/s 之間），頻譜中有兩個主要頻率成分: 較小的頻率非常接近漩渦脫落頻率， 隨著流速增加而增加且幅值較小；較大的頻率在0.15 rad/s 附近波動，基本和管道固有頻率 （1 000 m 管道的固有頻率為0.154 rad/s）相同，且隨流速變化不明顯，其與線性化矩陣的有阻尼特征值結果吻合較好。 也就是說在小流速時，立管的振動為概周期運動，其頻率成分包括:渦激頻率和立管頻率，此時相當于漩渦脫落激勵立管振動。 因流體阻尼作用小，流體與立管相互作用較弱，響應中保留了立管的頻率成分；

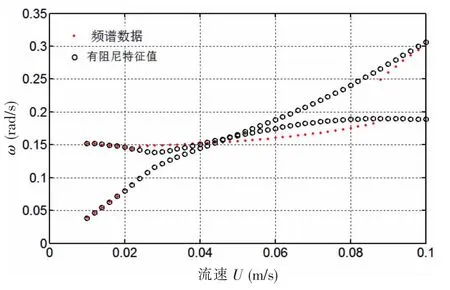
圖7 響應頻率變化Fig.7 Variation of response frequency

（2） 當流速處在較大范圍時（0.024-0.086 m/s 之間），此流速范圍立管振動處在“鎖頻”區域，振幅較大，響應頻率成分以基頻為主，其頻率值由U=0.024 m/s 時的0.148 rad/s 增大到了U=0.086 m/s 時的0.183 rad/s，略小于線性化矩陣的有阻尼特征值結果。 也就是說在中等流速下，立管的振動為周期運動，漩渦脫落頻率與立管頻率接近而發生“鎖頻”現象， 即發生共振；

（3） 隨著流速的增大（0.088-0.1 m/s 之間），此流速范圍管道振動脫離“鎖頻”區域，立管振幅幅值較小。 其頻譜圖像又發生了進一步的變化，主要頻率從0.088 m/s 時的0.249 rad/s 躍變為0.1 m/s 時的0.302 rad/s，得到的頻率接近于漩渦脫落頻率Ωf=2πStU/D（Ωf=0.340-0.387 rad/s），處于線性化矩陣有阻尼特征值之間，接近較大的特征值。 也就是說在小幅周期振動區間，即在高流速下，由于系統的耦合性，立管振動響應的主要頻率接近漩渦脫落頻率，并且立管頻率部分被衰減掉。

同時又提取了立管和尾流振子頻譜分析中主頻率對應的相位差， 并分析了其值隨流速變化的規律，如圖8 所示。 從圖中可以看出，在選取流速范圍內， 二者振動相位之間的關系是隨著流速逐漸變化的。 當流速為0.03-0.048 m/s 之間時，二者振動相位是同相的；當流速為0.048-0.096 m/s 之間時，二者振動相位是相反的。當v=0.096 m/s 時，立管位移-尾流振子位移的相位差達到了180°，二者相位完全相反。

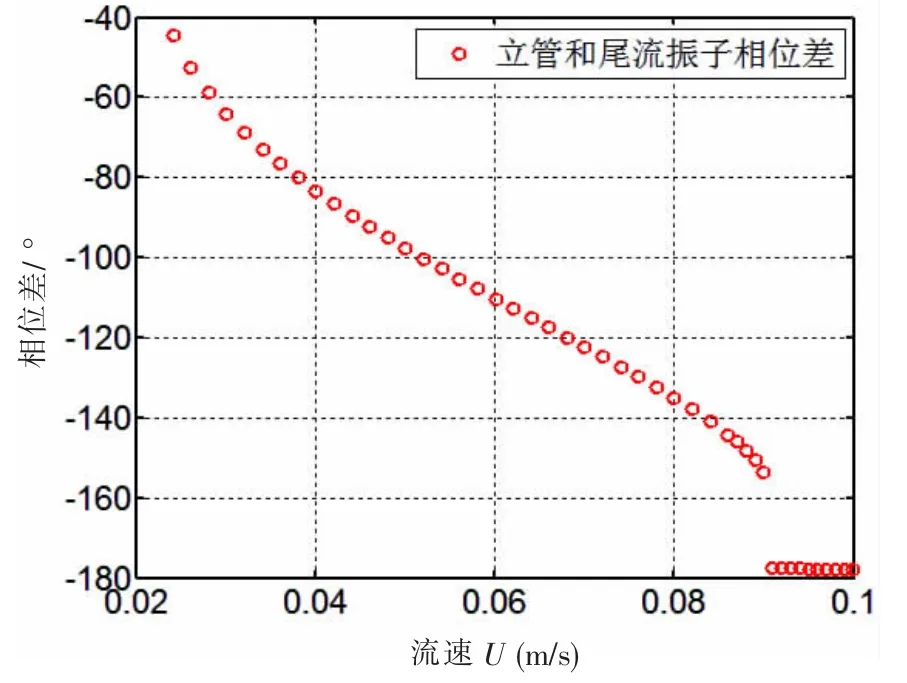
圖8 立管和尾流振子相位差隨流速變化圖Fig.8 Phase difference of riser and wake oscillator with flow velocity

4 結 論

本文利用Van der Pol 尾流振子模型描述流體的作用，建立了深海立管的渦激振動動力學模型，利用Poincaré 映射方法，研究了流速變化引起立管振動行為的分岔現象，并具體分析了振動響應頻率和相位的變化規律，主要結論如下:

（1） 無阻尼情況下，系統特征值隨流速變化，純虛特征值逐漸接近至相等，然后變成兩對虛部相等的復重根，再變為兩對純虛根。 U∈（0.025-0.085 m/s）間屬于耦合顫振平衡點不穩定，而其他區間平衡點是中心穩定的；有阻尼時，由于始終有一對復根實部大于0，平衡點始終是不穩定的，即立管處于渦激振動狀態。

（2） 通過本文的計算和研究表明:1000m 長管道系統響應存在三個區域，小流速下概周期運動，中流速下大幅鎖頻周期運動，高流速下小幅周期運動。 在鎖頻區兩側，分別存在兩種類型的雙穩態現象:概周期運動與大幅周期運動共存，大幅與小幅周期運動共存。

（3） 通過對系統響應頻率進行計算分析可知，系統處于小流速時，振動為概周期運動，頻率成分包括:渦激頻率和立管頻率，相當于渦脫落激勵立管振動；中等流速下，振動為大幅周期運動，渦脫落頻率與立管頻率接近而發生鎖頻現象，即發生共振；高流速下，振動為小幅周期運動，僅含渦脫落頻率，立管頻率部分被衰減掉。

（4） 在選取流速范圍內，立管和尾流振子振動相位之間的關系是隨著流速逐漸變化的，由小流速下的同相位變成了大流速下相反的相位。