基于BS 7608標準及利用結構對稱性對轉向架構架疲勞試驗的強度評估

王騰飛， 肖緋雄， 肖 茂

(西南交通大學 牽引動力國家重點實驗室， 成都 610031)

隨著我國鐵路客貨列車高速化的發展，機車車輛的運行工作環境不斷惡化，尤其是轉向架構架，在其服役不久就發生疲勞斷裂。對于轉向架構架疲勞強度的計算，國際鐵路聯盟UIC 515-4[1]標準規定了垂向載荷、橫向載荷、扭曲載荷及各載荷靜態、準靜態、動態值，且表明了各載荷的加載方式和循環次數。

BS 7608[2]標準是英國《鋼結構疲勞設計和評定實用規程》，該標準將焊接結構細節分為10個等級，并給出了相應的10個焊接結構細節相應的S-N曲線。S-N曲線不僅考慮了局部應力集中，尺寸與形狀的最大不連續值，而且還考慮了應力方向、冶金影響、殘余應力、疲勞裂紋形狀，以及某些等級下的焊接工藝和焊后處理方法。

將UIC 515-4規定的載荷譜通過有具有對稱結構的有限元分析得到關鍵點的應力譜，依據BS 7608標準中提供的焊接接頭疲勞性能參數，為構架關鍵部位進行疲勞強度評估。

1 構架疲勞試驗載荷

1.1 疲勞計算載荷

UIC 515-4標準中使用垂向載荷Fz、橫向載荷Fy和扭曲載荷Fw模擬轉向架構架疲勞載荷。垂向載荷由靜態載荷Fz及周期循環的準靜態載荷Fzq和動態載荷Fzd組成，橫向載荷由周期循環的準靜態載荷Fyq及動態載荷Fyd組成，其載荷大小隨時間變化規律如圖1所示。

UIC 515-4標準將疲勞試驗加載分為3個階段。第1階段：動態載荷循環次數為6×106次。第2階段：動態載荷循環次數為2×106次，垂向與橫向靜載荷值不變，準靜態載荷值與動載荷值為第1階段的1.2倍。第3階段：動態載荷循環次數為2×106次，垂向與橫向靜載荷值不變，準靜態載荷值與動載荷值為第1階段的1.4倍。

圖1 構架疲勞試驗各載荷加載示意圖

1.2 載荷等級劃分

選取線路狀況為：垂向與橫向準靜態載荷每循環1次，垂向與橫向動載荷循環20次，垂向載荷與橫向載荷的頻率與相位均相同，左、右曲線準靜態與動態載荷模擬次數相同，扭曲載荷循環次數為垂向與橫向動態載荷的1/10。用雨流計數法對上述載荷循環過程計數，構架每階段載荷等級可分為7級[3]，得到的載荷譜見表1。

表1 構架第1階段疲勞試驗載荷譜

注：第2階段與第3階段準靜態與動態載荷值分別為表1中1.2與1.4倍，循環次數為表1 1/3。

2 疲勞強度評估方法

2.1 名義應力

名義應力是依據材料力學用簡單公式進行計算母材受載橫截面的名義應力，即軸向力除以橫截面，彎矩或扭矩除以有關截面模量[4]。BS 7608標準中焊接結構細節的S-N曲線是基于名義應力創建的，忽略焊接結構接頭應力集中造成的影響。

2.2 S-N曲線

BS 7608標準根據應力范圍(Δσmax-Δσmin)評定焊接接頭疲勞特性，且考慮了應力范圍低于疲勞極限(循環次數N=107失效時對應的應力范圍)對疲勞累計損傷的貢獻。在N=107時，S-N雙對數曲線由斜率m變化到m+2，S-N曲線如圖2所示。

圖2 BS典型的雙斜率Δσi-N曲線

BS 7608標準定義疲勞損傷計算公式如式(1)～式(2)：

(1)

(2)

式中：Δσ0為N=107對應的應力范圍;Δσi為名義應力范圍;ni為名義應力范圍Δσi在應力譜中出現的循環次數;Ni為名義應力范圍Δσi在S-N曲線中對應的循環次數;m為S-N曲線的斜率。

3 結構對稱性的利用

在有限元分析過程中，有限元的計算時間和節點數有很大的關系，因此在保證計算精度的條件下，不宜采用過多的節點，用來節約時間資源。當結構具有對稱性時，可以利用此特點來減少計算的節點數[5]。結構的對稱性是指結構的幾何形狀和支撐關于某軸對稱，同時截面和材料性質也關于此軸對稱。具有對稱性的結構依據載荷情況的不同，可分為軸對稱問題，對稱問題，逆對稱問題和周期對稱問題。

3.1 對稱載荷及反對稱載荷

對稱載荷是指結構繞對稱軸對折后，左右兩部分的載荷作用點相重合，方向相同，荷載數值相同。根據彈性力學對稱性原理，受載后結構的變形必然也是對稱的，同時結合變形協調原理，可以得出在對稱面的位移邊界條件為UY=0、ROTX=0、ROTZ=0(假設對稱軸為Y軸)，如圖3所示。

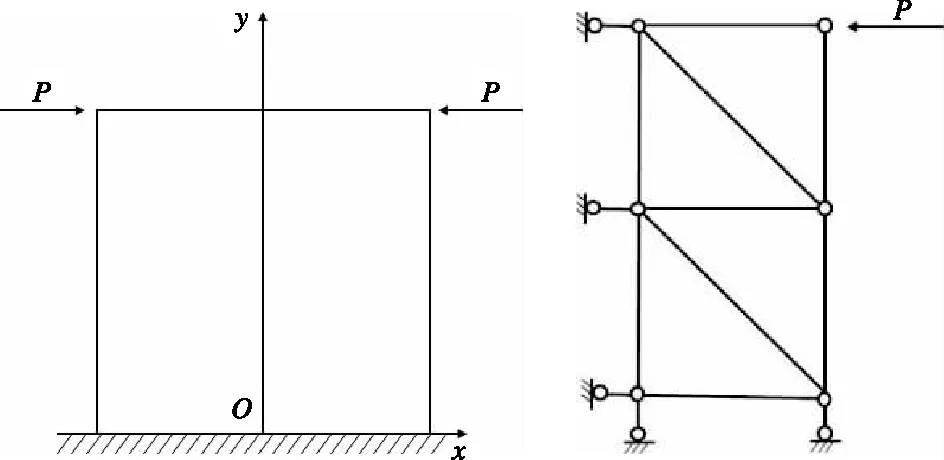
圖3 對稱載荷的有限元劃分

反對稱載荷是指結構繞對稱軸對折后，左右兩部分的載荷作用點相重合，方向相反，荷載數值相同。根據彈性力學對稱性原理，受載后結構的變形必然也是反對稱的，同時結合變形協調原理，可以得出在反對稱面的位移邊界條件為UX=0、UZ=0、ROTY=0(假設對稱軸為Y軸)，如圖4所示。

圖4 反對稱載荷的有限元劃分

3.2 非對稱載荷

在一般情況下，外載荷通常是不具備對稱性或反對稱性的非對稱載荷。這時，可利用線彈性范圍內的可疊加原理，將非對稱載荷分解為對稱載荷及反對稱載荷，然后按照對稱性與反對稱性進行疊加，就可以得到非對稱載荷下的結構的位移及應力，如圖5所示。

圖5 非對稱載荷的劃分

4 算 例

對某型地鐵列車轉向架構架進行有限元強度分析，依據UIC 515-4標準中的計算公式，第1階段作用于構架側梁上的垂直載荷為Fz=118.0 kN，Fzq=11.8 kN，Fzd=23.60 kN；橫向載荷為Fyq=39.3 kN，Fyd=39.3 kN，扭曲載荷按照軌道扭曲量的5‰。第2階段與第3階段的載荷分別為第1階段的1.2與1.4倍。

4.1 構架有限元建模

BS 7608對焊接結構進行疲勞分析過程中，確定疲勞壽命時只需考慮循環主應力的范圍，忽略平均應力的影響。在彈性力學空間問題基本理論[6]中指明，若已知某點的應力分量，則該點的主應力是確定的且不隨坐標的改變而改變。對于表1中各不同方向的載荷，基于彈性力學疊加原理，并結合Ansys后處理模塊中Load case功能，可同時將不同方向載荷產生的在整體坐標系下的各應力分量進行相應線性疊加，得到某點在組合載荷下的應力分量狀態，進而可以繼續求解出唯一確定的主應力值及其方向，故可以把表1的載荷值等效轉變為垂向載荷范圍ΔFzd、ΔFzq，橫向載荷范圍ΔFyd、ΔFyq，扭曲載荷范圍ΔFw，簡化的載荷譜如表2。同時將結構對稱性的理論應用于構架各組載荷[7]，用四面體單元solid95對構架進行有限元離散，得到有限元模型如圖6。

表2 第1階段簡化載荷譜

圖6 構架有限元模型

4.2 邊界約束條件

在有限元計算模型中，由于此例采取實體單元建模，故對于垂向載荷ΔFz只需在對稱面(YOZ，XOZ)建立對稱約束(UX=0，UY=0)。對于橫向載荷ΔFy分為對稱載荷與反對稱載荷，對稱載荷需在對稱面(YOZ，XOZ)建立對稱約束(UX=0，UY=0)，反對稱載荷需在對稱面(YOZ，XOZ)建立反對稱約束(UX=0，UX=0且UZ=0)。扭曲載荷ΔFw作用于軸箱彈簧處，分為對稱載荷與反對稱載荷，對稱載荷需在對稱面(XOZ)建立對稱約束(UY=0)，反對稱載荷需在對稱面(XOZ)建立反對稱約束(UX=0且UZ=0)。

4.3 疲勞強度的評估

對構架的上下蓋板焊縫及母材進行疲勞強度評估，將評估點的焊接結構細節與BS 7608標準中提供的結構細節對比，選擇合適的焊縫等級進行疲勞壽命計算[8-9]，選取焊縫的疲勞強度等級為F，母材的疲勞強度等級為C，焊接接頭結構分類細節選取說明如表3所示。根據UIC 515-4標準對構架疲勞試驗結果的說明，即在第3階段試驗時，如果出現不影響工作的小裂紋也是允許的，同時在依據BS 7608標準中焊趾打磨對改善焊縫的影響，即通過局部機械加工或打磨焊趾，可使S-N曲線疲勞強度提高30%，可得出焊縫疲勞強度等級參數，如表4所示。

表3 BS 7608焊接接頭結構分類細節

表4 疲勞強度等級參數

在Ansys中輸出每組載荷下評估點在整體坐標系下6個應力分量，進行疊加繼而在求出各點的主應力，利用2.2節敘述的疲勞損傷計算式(1)和式(2)，得出關鍵評估點的損傷結果如表5所示。

表5 構架關鍵位置評估點損傷比

圖7 構架焊縫疲勞強度計算部分取值點

從構架關鍵點損傷比可以看出，構架疲勞累計損傷均小于1，疲勞強度滿足設計要求。但靠近二系簧側梁與上蓋板連接處焊縫區域疲勞強度余量不足，可對轉向架進行適當的局部修改，增強抗疲勞能力。

5 結 論

依據UIC 515-4標準中規定的構架疲勞試驗載荷，在有限元方法中利用結構對稱性求出整體構架應力分布，用BS 7608標準計算構件關鍵評估點的累計損傷比，依據累計損傷比是否超過1，可以有效的判斷構架關鍵部分的疲勞強度。

將結構對稱性用于有限元計算中，大大的減少了構架在計算中的時間與空間成本，在工程設計中可以有效的減少產品研發周期和開發研制成本。