基于有限元法的高速動車組受電弓仿真分析
李笑顏, 王俊勇, 蘇安社, 高文斌, 吳榮平, 賈 榮, 黃思俊
(1 西南交通大學 機械工程學院, 成都 610031;2 北京中車賽德鐵道電氣科技有限公司, 北京 100176)
隨著我國高速電氣化鐵路的快速發展,如何保證動車組受電弓在高速狀態下的受流,已成為一個日益重要的課題。國內學者建立了多種不同的受電弓數學模型,仿真模擬受電弓和接觸網的運行狀態。其中,運用最為廣泛的是歸算質量模型。對于歸算質量模型來說,分為弓頭和框架部分的二質量塊模型;弓頭、上框架和下框架的三質量塊模型。以往的歸算質量模型參數,是通過對實物受電弓進行參數測量試驗獲得,這就要求受電弓廠家必須先生產出受電弓實物再進行相關測試,然后根據測試結果和弓網仿真結果調整相應的設計參數,這就大大增加了設計周期和財務成本。文中基于ANSYS等軟件,建立一種有限元方法計算受電弓歸算質量模型參數,并與試驗測試數據對比,驗證方法合理性。該方法基于受電弓三維模型進行計算,無需生產樣機,方便調整設計參數,減少了設計周期和財務成本。
1 三質量塊模型簡介
歸算質量模型是在受電弓某個工作高度時,將其等效成以彈簧阻尼系統相連接的等效質量模型。三質量塊模型通常把弓頭等效成一個質量塊,上臂桿與下臂桿分別等效成一個質量塊,如圖1所示。歸算質量模型具有自由度少、計算效率高的優點。
圖1中,m1,c1,k1分別為弓頭部分的等效質量、等效阻尼、等效剛度;m2,c2,k2分別為上框架部分的等效質量、等效阻尼、等效剛度;m3,c3,k3分別為下框架部分的等效質量、等效阻尼、等效剛度。

圖1 受電弓三質量塊模型
2 受電弓等效參數計算
受電弓三質量塊等效參數在各個工作高度會存在差異。文中以380 km/h高速動車組DSA380受電弓為研究對象,利用ANSYS等軟件計算其在1 600 mm工作高度下的三質量塊等效參數。
2.1 弓頭等效質量
弓頭的垂向等效質量即為其實際質量,將DSA380受電弓弓頭三維模型導入三維建模軟件CATIA并賦予每個零件相應材料即可測得其質量me1為7.71 kg。
2.2 弓頭等效剛度
弓頭等效剛度即為弓頭彈簧的垂向剛度。將弓頭模型導入ANSYS,在頂管處施加固定約束,在兩條滑板中部施加垂直向下的作用力,測得滑板垂向位移即可得到弓頭的力-位移曲線,力與位移的比值即為弓頭剛度,測得弓頭等效剛度K1為6 635 N/m。

圖2 計算受電弓弓頭剛度

圖3 受電弓弓頭剛度計算結果
2.3 弓頭等效阻尼
將弓頭模型導入ANSYS,固定頂管后給碳滑板一個垂直向下的激勵使其在垂直方向自由振動。在后處理模塊中輸出碳滑板位移-時間曲線。根據振動力學公式
(1)
計算得衰減系數δ1=0.124。根據公式
(2)
將K1=6 635 N/m,m1=7.71 kg代入式(2)計算得弓頭等效阻尼C1為8.93 N·s/m。
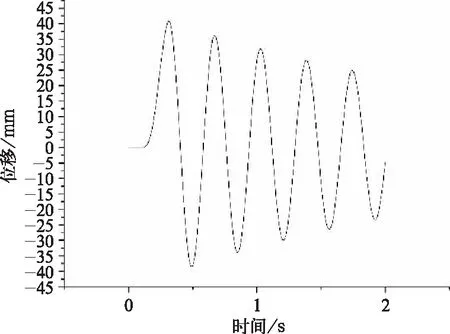
圖4 受電弓弓頭振幅曲線
2.4 框架整體等效質量
受電弓框架可視為只具有垂直方向位移自由度的單自由度系統。其自由振動微分方程表達式為

(3)
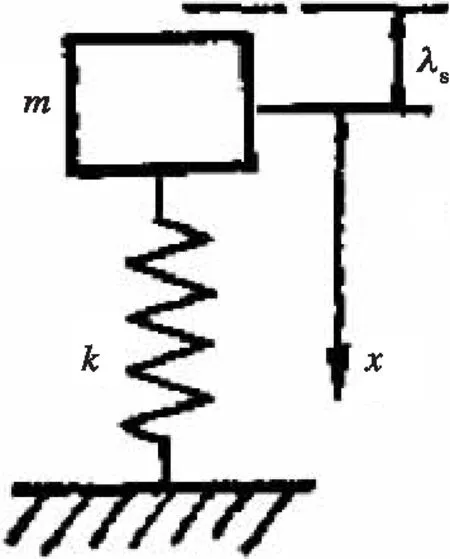
圖5 質量塊模型原理圖
將受電弓模型導入ANSYS瞬態動力學模塊,設置好各關節部位的運動副,調整其達到1 600 mm的工作高度。用剛度為3 000 N/m的彈簧懸吊在頂管處,使受電弓在這一高度達到平衡。在頂管處施加垂向載荷使受電弓作垂向自由振動,后處理模塊輸出其振動周期T1=0.414 s, 根據振動力學公式
(4)
將K=3 000 N/m,T1=0.414 s代入式(4)計算得m2為13.02 kg。由于模型中未添加弓頭彈簧,故框架整體等效質量me2應為m2與弓頭彈簧質量m之和
me2=m2+m
(5)
計算得框架整體等效質量me2為13.98 kg。
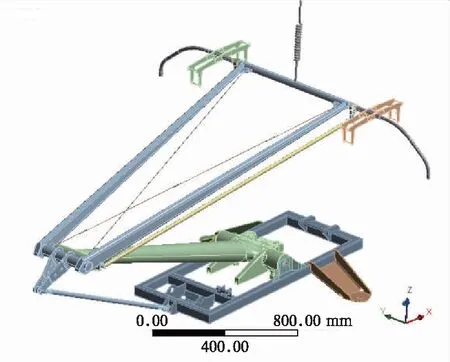
圖6 計算受電弓框架整體等效質量
2.5 上框架等效剛度
將受電弓模型導入ANSYS穩態動力學模塊,下框架和底架部分設置為剛體,固定受電弓下框架與底架連接處的鉸,頂管處施加初始垂向載荷,在后處理模塊中輸出上框架在垂向載荷作用下的垂向位移,即可得到受電弓上框架等效剛度。計算得DSA380受電弓上框架剛度K2=14 675 N/m。
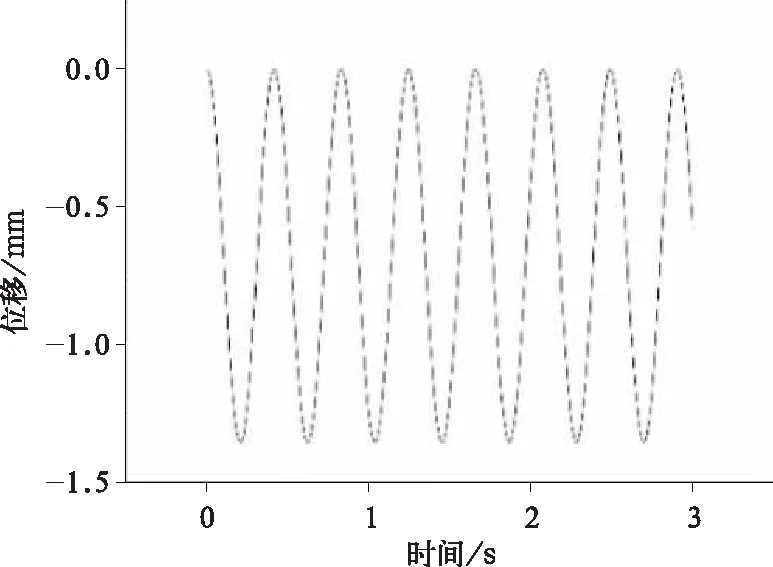
圖7 受電弓框架整體振動周期
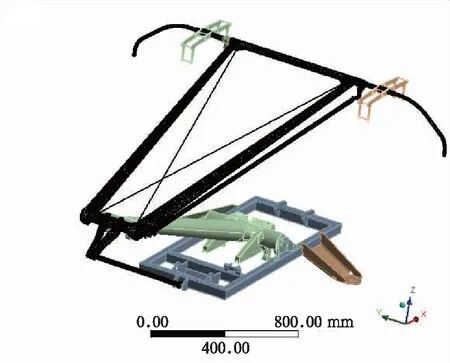
圖8 計算受電弓上框架剛度
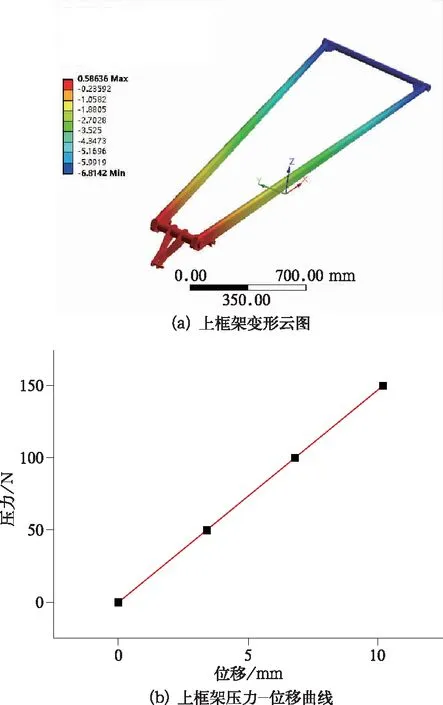
圖9 受電弓上框架剛度計算結果
2.6 上框架等效質量
計算上框架歸算質量采用與計算上框架剛度相同的模型,頂管處施加初始垂向載荷后使受電弓上框架部分產生垂向自由振動,在后處理模塊中輸出自由振動波形,得到其振動周期T2=0.144 s,由公式
(6)
將K2=14 675 N/m,T2=0.144 s代入式(6)計算得質量m3為7.71 kg;由于模型中未添加弓頭彈簧,故上框架等效質量me3應為m3與弓頭彈簧質量m之和
me3=m3+m
(7)
計算得上框架等效質量me3為8.67 kg。

圖10 受電弓上框架振動周期
2.7 上框架等效阻尼
將受電弓模型導入ANSYS,在材料屬性中定義上框架部分各零件的材料阻尼,將下框架固定,采用QRDAMP法對受電弓進行模態分析,得到其模態阻尼比。取一階阻尼比ξ=0.010 36,根據公式
(8)
將K2=14 675 N/m,me3=8.67 kg代入式(8)計算得上框架等效阻尼C2為17.58 N·s/m。

圖11 計算受電弓上框架阻尼

階數阻尼比ξ1.0.01042.0.03203.0.03624.0.07935.0.0568
2.8 下框架等效剛度
在受電弓工作范圍內,理想狀態下受電弓工作時的靜態接觸力為常數,下框架的等效剛度為 0。但受實際工作條件限制,受電弓靜態接觸力存在微小變化,導致下框架剛度不為0,一般其值在50~150 N/m范圍內,取其值為100 N/m。
2.9 下框架等效質量
框架整體等效質量減去上框架等效質量即為下框架等效質量。
me4=me2-me3
(9)
將me2=13.98 kg,me3=8.67 kg代入式(9)計算得下框架等效質量me4為5.31 kg。
2.10 下框架等效阻尼
受電弓下框架的阻尼主要由阻尼器產生,將受電弓模型導入ANSYS瞬態動力學模塊,采用彈簧阻尼單元模擬受電弓阻尼器。根據DSA380受電弓四連桿模型測得其在1 600 mm工作高度時的阻尼器長度,并由阻尼器廠家提供的阻尼器參數得到其在這一長度附近的阻尼值為16 000 N·s/m。采用剛度為3 000 N/m的彈簧懸吊在受電弓框架頂部,施加垂向載荷使其自由振動,輸出振動波形,測得振幅衰減。
(10)
由式(10)計算得衰減系數δ2=0.54
(11)
將K=3 000 N/m,me2=13.98 kg代入式(11)計算得下框架等效阻尼C3為35.2 N·s/m。
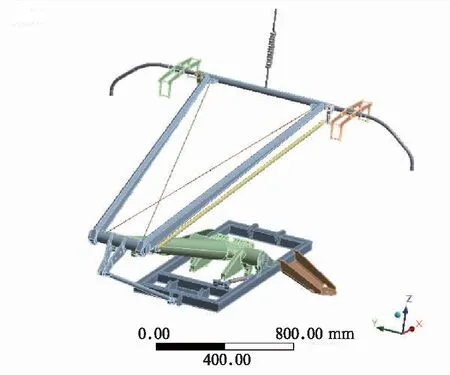
圖12 計算受電弓下框架阻尼
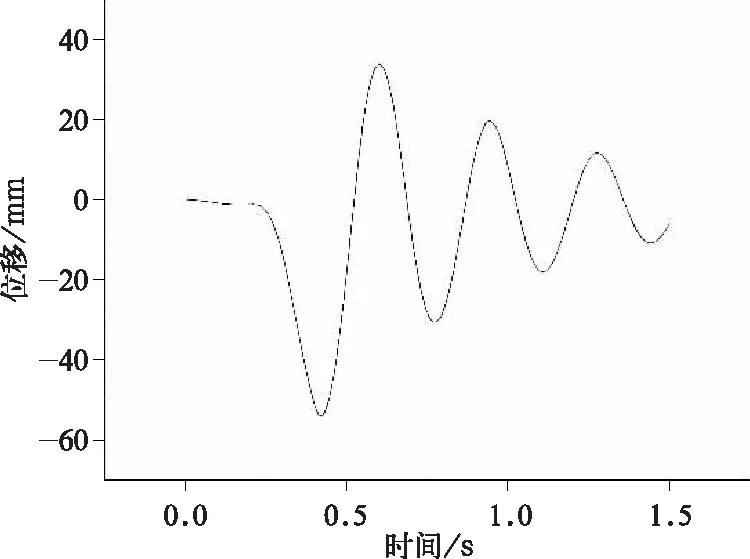
圖13 受電弓下框架振幅衰減
3 受電弓等效參數計算誤差分析
為驗證DSA380受電弓三質量塊模型參數仿真結果的準確性,對受電弓進行三質量塊參數測試試驗并比較兩組數據之間的誤差。試驗所得數據與仿真數據如表2所示。

表2 三質量塊試驗參數與仿真參數對比
3.1 誤差分析
對比表2中試驗數據與仿真數據可知,通過有限元方法對高速動車組受電弓三質量塊模型參數進行分析的誤差一般不超過15%。其中,仿真方法在計算等效質量與等效剛度方面與試驗結果之間誤差較小,考慮誤差產生的主要因素為模型精度及網格質量;在計算阻尼參數時,DSA380受電弓弓頭阻尼的試驗測試數值與仿真分析數值之間差距較大,分析其原因為弓頭彈簧零部件之間摩擦阻尼較大,該部分阻尼在仿真軟件中無法完全模擬,方法有待改善;受電弓上框架仿真得到的阻尼與試驗值誤差分析為試驗工裝阻尼及零件摩擦產生的阻尼;下框架阻尼誤差分析為仿真時未考慮氣囊排氣產生的阻尼及對阻尼器阻尼線性取值導致。
4 結 論
通過有限元仿真法計算了DSA380受電弓三質量塊模型等效參數,與試驗數據對比,仿真方法在計算等效質量及等效剛度時較為精準,說明方法對指導受電弓的設計具有一定意義,但在計算弓頭等效阻尼時誤差較大,方法有待進一步改善。

