亞軌道高動態飛行器攔截彈道模式研究
余卓陽,謝 放,許 偉,田 博,郭 昊
(空間物理重點實驗室,北京,100076)
0 引 言
亞軌道高動態飛行器飛行速度快,機動能力強,飛行高度高于防空導彈最大作戰高度,能突破現有的防空系統,具有重要的軍事價值。為應對亞軌道高動態飛行器的威脅,需開展針對該飛行器防御技術的研究[1~4]。攔截彈彈道模式是影響攔截效果的重要因素,因此,近年來,針對亞軌道高動態飛行器攔截彈道的研究成為熱點[5~8]。戴靜等[4]在研究亞軌道飛行器攔截問題時借鑒了攔截彈道導彈的思路,設計的攔截彈道模式與彈道導彈末端攔截模式相似,由于亞軌道飛行器軌跡與彈道導彈有明顯不同,直接沿用原有的彈道模式造成攔截彈射程偏小,防御范圍不夠。由于亞軌道飛行器飛行特性與飛機有相似之處,熊俊輝等[7]提出利用空基攔截器進行攔截的思路,攔截彈彈道模式與空空導彈類似;黃春華等[6]為擴大攔截彈射程,采用將攔截彈助推到大氣層外再入的方式進行攔截,攔截彈道模式為高拋彈道或再入平飛彈道。上述兩種模式擴大了攔截彈射程但沒有考慮亞軌道飛行器攔截對防御系統的探測,跟蹤提出的巨大挑戰,對攔截作戰過程中探測、預警、跟蹤等其它環節關注不夠,而攔截彈作為整個防空反導系統的一環,其彈道模式設計應考慮系統的探測跟蹤目標能力并與其相匹配。
防空反導系統根據其探測跟蹤目標能力不同,有傳統視距攔截和超視距攔截兩種作戰模式。傳統視距攔截作戰模式下制導所需的目標信息由單一攔截陣地的火控雷達提供。亞軌道目標飛行高度低,考慮地球曲率的限制,雷達對其最大探測距離約為700 km。另一方面,亞軌道高動態目標飛行速度快,因此,其在火控雷達探測范圍內飛行的時間有限,這對攔截系統快速響應提出了很高的要求。
近年來,超視距攔截作戰模式[9]成為防空反導作戰的研究熱點。在超視距攔截作戰模式中,可由外部探測系統提供目標信息,指揮系統根據獲得的目標信息,在攔截陣地的火控雷達還未探測到目標時即可發射攔截彈。攔截陣地的火控雷達無需跟蹤目標,而僅需跟蹤攔截彈[10]。該作戰模式突破了單一雷達對目標探測范圍的限制,放寬了對攔截系統快速響應的要求,可以擴大攔截彈作戰范圍。
針對上述兩種模式設計的攔截彈彈道模式,本文利用參數優化方法和最優控制理論分別對上述兩種作戰模式下的攔截彈道進行設計,對亞軌道高動態飛行器防御技術研究有一定的參考價值。
1 攔截彈模型
1.1 總體模型
攔截彈采用兩級固體火箭發動機助推,助推結束后動能殺傷器(Kinetic Kill Vehicle,KKV)分離并利用姿軌控發動機控制直接碰撞目標。
1.2 運動學和動力學模型
1.2.1 基本假設
為突出主要矛盾,降低彈道設計難度,做出如下基本假設:
a)地球為一均質不旋轉圓球;
b)攔截彈,目標在同一垂直平面內飛行;
c)大氣模型使用指數大氣模型。
1.2.2 運動學和動力學方程
基于1.2.1節的假設,飛行器運動學和動力學方程如式(1)~(4)所示。

2 傳統視距攔截作戰彈道設計
由于單一雷達探測范圍有限,攔截彈最大飛行時間受到約束。考慮目標平飛,攔截彈與目標在同一平面運動的情況,根據圖1所示的幾何關系,可得:


圖1 攔截過程幾何關系Fig.1 Geometrical Relationship Between Interceptor and Target
2.1 彈道模式分析
攔截彈彈道根據飛行中高度變化情況可分為自由飛彈道、平飛彈道和高拋彈道 3類[11,12]。自由飛彈道軌跡近似于直線,飛行路程最短但阻力損失大;高拋彈道急劇爬升再回到目標高度,阻力損失小,能量優勢大,但增加了飛行路程,飛行時間長。平飛彈道先上升到目標高度后平飛與目標交會,是一種折中的彈道模式。仿真結果表明,高拋彈道飛行時間不能滿足攔截彈最大飛行時間約束,因此,選擇平飛彈道和自由飛彈道進行設計。
2.2 平飛彈道設計
2.2.1 一級助推段彈道設計
在一級助推段,攔截彈歷經亞聲速、跨聲速、超聲速和高超聲速,氣動特性復雜,直接對攻角進行優化難度較大。因此,首先對攻角進行參數化,然后利用參數優化的方法設計助推段飛行程序。采用亞、跨聲速零攻角飛行,超聲速氣動轉彎的方案,攻角可以表示為[13]
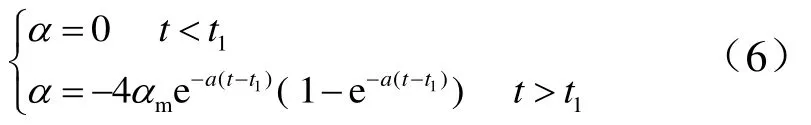
一級助推段攻角設計需滿足的約束條件如下:
a)最大攻角約束:

b)跨聲速段零攻角約束:

c)級間分離小攻角約束:

優化目標為一級助推結束時能量最大:
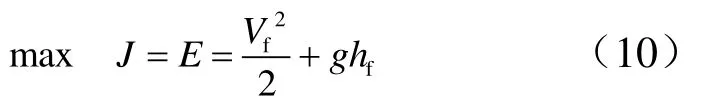
2.2.2 級間段和二級助推段彈道設計
在級間滑翔段和二級助推段,攔截彈速度已達到高超聲速,根據馬赫數無關原理,氣動系數只與攻角相關,可以利用最優控制理論直接對攻角進行優化。
級間段和二級助推段彈道優化可以轉化為一個最優控制問題。
系統狀態方程包括式(1)~(4)及攔截彈質量方程:

式中ms為推進劑秒流量。
為保證攻角連續變化,取攻角為狀態變量,攻角的導數為控制量:

由式(1)~(4)、(11)、(12)構成系統狀態方程。
在平飛彈道中,KKV平飛段射程占據整個射程的60%左右,為提高射程,需提高KKV分離速度。將目標函數取為末速最大和控制能量消耗最少:
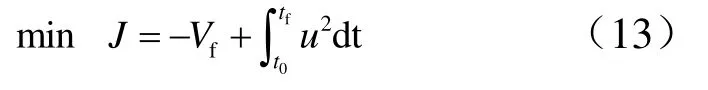
式中u為控制變量。
約束分為過程約束和末端約束,過程約束如下:
a)最大攻角約束:

b)最大攻角變化率約束:

c)級間段零攻角約束:

末端約束如下:
a)為保證在KKV分離后,KKV能耗費較少燃料在目標高度H平飛,KKV分離時高度和彈道傾角需滿足:

b)KKV分離小攻角約束:

可以利用高斯偽譜法[15]求解式(1)~(4)、式(11)~(19)定義的最優控制問題。
2.2.3 KKV平飛段彈道設計
為實現KKV在目標高度H平飛,須滿足:
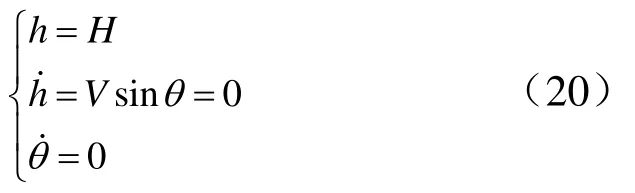
由式(20)可得,需用過載可以分成兩部分:
a)平衡重力,離心力,保證彈道傾角變化率為
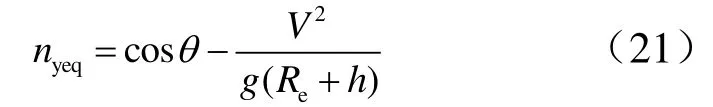
b)調整導彈高度到目標高度滿足:
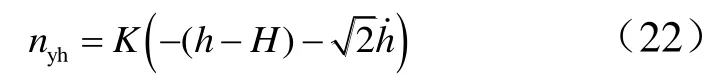
則KKV需用過載為

末端約束如下:
a)為保證在KKV分離后,KKV能耗費較少燃料在目標高度H平飛,KKV分離時高度和彈道傾角需滿足:

b)KKV分離小攻角約束

可以利用高斯偽譜法[15]求解式(1)~(4)、式(11)~(19)定義的最優控制問題。
2.3 仿真結果
取目標高度40 km,利用2.2節方法對彈道進行設計,并與自由飛彈道進行對比,仿真結果如圖2~5所示。由于自由飛彈道保持0°攻角飛行,因此圖4中只繪出了平飛彈道的攻角曲線。彈道對比結果如表1所示。

表1 彈道對比結果Tab.1 Contract Result of Trajectory
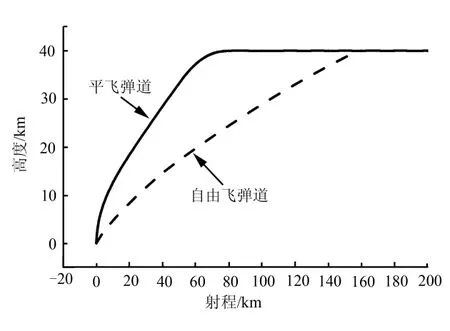
圖2 射程-高度曲線Fig.2 Altitude VS Range

圖3 時間-速度曲線Fig.3 Velocity VS Time

圖4 時間-攻角曲線Fig.4 Attack Angle VS Time
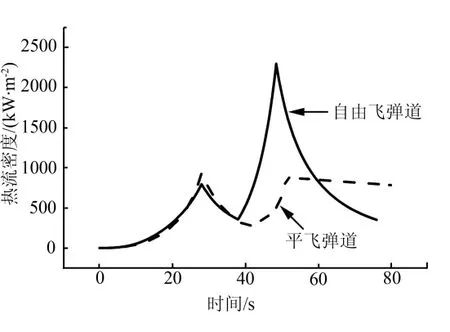
圖5 熱流密度Fig.5 Heat Flux
由圖2~5可知,平飛彈道在射程和末速方面相比自由飛彈道分別提高了27%和29%,而自由飛彈道動熱流顯著高于平飛彈道,其峰值熱流是平飛彈道的2.5倍。同時,平飛彈道通過調整KKV平飛時間即可覆蓋82~200 km的射程范圍,提高了作戰靈活性。綜上,平飛彈道相比自由飛彈道有顯著的優勢,是適合傳統視距作戰的彈道模式。
3 超視距攔截作戰彈道設計
3.1 彈道模式分析
超視距攔截作戰模式由于突破了單一雷達探測范圍的限制,可放寬攔截彈最大飛行時間的限制以發揮攔截彈能量優勢,實現遠程攔截。
3.2 高拋彈道
高拋彈道一級助推段設計方法與2.2.1節相同。級間段,二級助推段,KKV飛行段設計方法與2.2.2節相似,但 KKV分離后不平飛,因此,去掉式(17)、(18)的約束。同時,優化目標可選取末端射程最大和控制能量消耗最小的綜合指標,即:
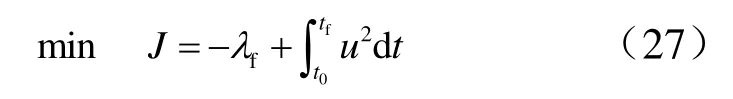
利用高斯偽譜法求解上述最優控制問題即可實現對高拋彈道的設計。延長2.2節平飛彈道KKV飛行時間至KKV燃料耗盡,高拋彈道與平飛彈道設計結果如圖6~9所示。
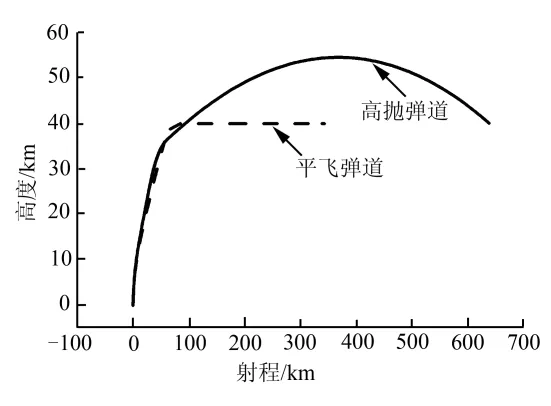
圖6 射程-高度曲線Fig. 6 Altitude VS Range
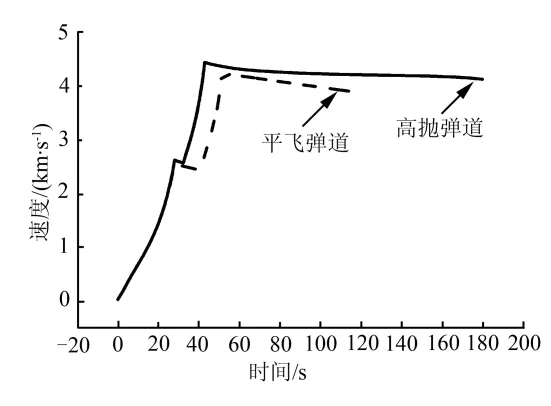
圖7 時間-速度曲線Fig.7 Velocity VS Time
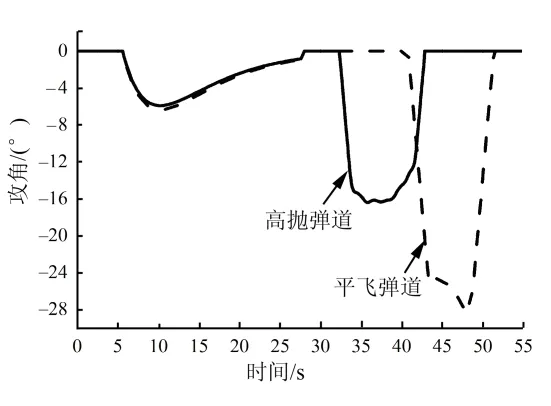
圖8 助推段時間-攻角曲線Fig.8 Attack Angle VS Time in Boost Phase

圖9 熱流密度對比Fig.9 Heat Flux
3.3 彈道模式對比
從圖9中可以得出,高拋彈道助推段最大熱流大于平飛彈道,但高拋彈道 KKV飛行高度高于目標高度,而平飛彈道KKV在目標高度平飛。因此,高拋彈道KKV飛行段平均熱流明顯低于平飛彈道。
與2.3節類似,兩種彈道模式的對比如表2所示,其中平均熱流指KKV飛行段平均熱流。
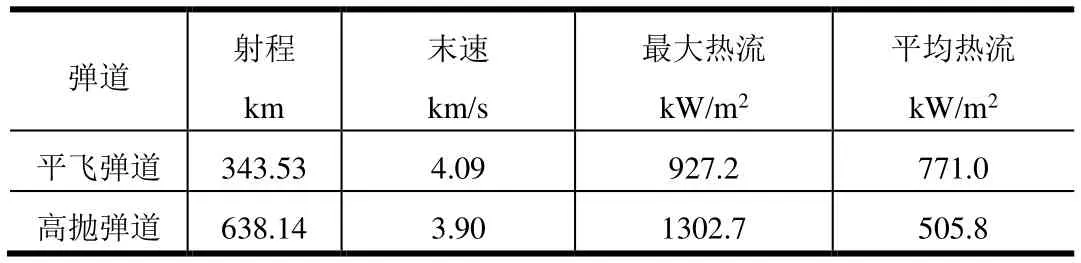
表2 彈道對比結果Tab.2 Contract Result of Trajectory
從表 2可以看出,高拋彈道射程為平飛彈道的1.8倍,末速比平飛彈道高近200 m/s,且KKV飛行段的平均熱流顯著低于平飛彈道。綜上,高拋彈道充分發揮攔截彈能量優勢,是更適合超視距攔截作戰的彈道模式。
4 結束語
對于亞軌道高動態飛行器攔截彈道模式而言,通過分析發現:a)對于傳統視距攔截作戰,平飛彈道相比自由飛彈道在射程、末速、熱流、動壓方面有顯著的優勢,且通過一條彈道可以覆蓋較大的射程范圍,是適合傳統視距攔截的彈道模式;b)對于超視距攔截,高拋彈道通過高空飛行減少阻力,可以充分發揮攔截彈能量優勢,在射程和末速方面有很大的優勢,是適合超視距攔截作戰的彈道模式;c)超視距攔截作戰能夠充分發揮攔截彈能量優勢,擴展攔截彈的射程。

