基于人群搜索算法的直流電機優化設計?
趙廣元 王 超
(西安郵電大學自動化學院 西安 710121)
1 引言
隨著計算機技術的飛躍發展,人工智能技術已逐漸滲透到自動控制領域[1]。近年來針對不同的控制要求、不同的系統先驗知識,研究人員提出了許多PID 控制器參數整定方法[2],根據發展階段的劃分,可分為常規PID 參數整定方法及智能PID 參數整定方法[3]。傳統的控制方法不能滿足控制精度的要求,而且抗干擾的能力較差[4]。因此,如何建立有效的直流電機控制系統的仿真模型成為研究人員迫切需要解決的關鍵問題[5]。
1992 年,瑞典學者Karl Astrom 等推出的智能型PID 參數整定控制器簡化了傳統PID 控制器的參數整定[6],將群智能優化算法應用于PID 參數整定優化已得到廣泛的認可和應用[7];程準等學者利用粒子群算法改進拖拉機驅動防滑的PID 控制器算法,提出了改進PSO 算法,加快了算法的收斂速度[8];白國振等利用改進的模糊神經網絡,對控制器PID 參數進一步的優化,提出了混沌人工魚群—模糊神經網絡算法,使得控制器具有良好的控制性、穩定性和有效性[9];朱堅民等人利用神經網絡動態改進球桿系統PID 控制器的算法,使得系統可以快速的響應并保持穩定的狀態[10]。
雖然以上方法在一定程度上克服了傳統PID的缺陷,但將其用于工業過程控制中,振蕩幅度和周期的測量值在噪聲環境下準確度會下降,顯然難以獲得滿意的控制效果。甚至當參數變化范圍太大時,系統性能會明顯變差[11]。
針對PID 控制器參數優化問題,本文根據具體的直流電機機械參數[12]并結合人群搜索算法(SOA)搜索最佳的PID 控制器參數。仿真結果表明,相比于傳統的PID 控制器參數整定優化方法,該算法優化的自抗擾控制器能夠更好地滿足控制要求,具有魯棒性好,響應速度快,系統具有更好的控制性能。
2 PID控制器
PID 控制器是通過對輸入信號值和輸出信號值之間存在的偏差信號,通過比例、積分、微分的方式實現對被控對象的控制[12]。經典的PID 控制原理如圖1所示。
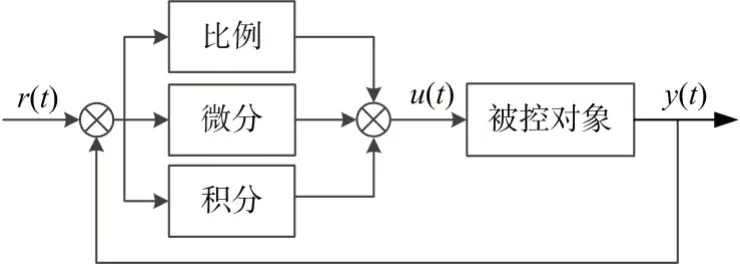
圖1 經典PID控制原理圖
PID控制器的控制規律可表示為
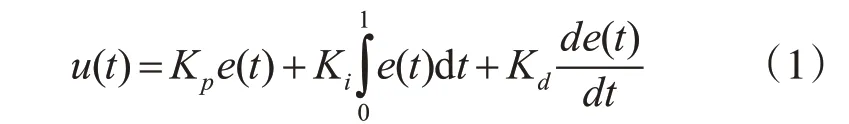
式(1)中,Kp,Ki和Kd三個參數分別是對輸入信號e(t)及其比例、積分、微分量的加權值,通過調整這三個參數可獲得最佳的控制效果[13]。
對式(1)進行拉普拉斯變化,將其轉換到頻域時,可得到直流電機頻域的傳遞函數。
3 人群搜索算法(SOA)
3.1 SOA的基本思想
SOA 是最近幾年提出的一種智能隨機搜索算法,人群搜索算法對人類的行為進行自主分析[13],利用人類的一系列優秀的行為,如:個體向優秀個體進化、優秀個體向優秀群體進化、優秀群體向優秀種群進化。所有的個體都參與搜索,通過個體來確定方向和步長的搜尋,實現所處位置的更新,以獲取所處范圍內的最優的解[14]。
3.2 SOA參數的確定
3.2.1 適應度函數的確定
為了防止控制能量的過大輸入,提高系統的穩定性,引入控制輸入平方項,性能指標函數為
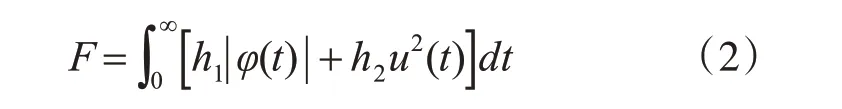
式(2)中,φ(t)是系統輸入和輸出之間的偏差;u(t)是SOA 控制器輸出值;h1、h2分別是各項權值,取值范圍為[0,1]。
為了避免超調量對系統帶來誤差,采用一定措施的懲罰控制,以增強系統的穩定性。當系統運行過程中發生超調時,選取最優指標為
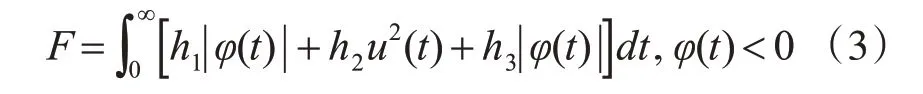
式(3)中,h3為每次新添加項權值,并且h3?h1,假設h1=0.999,h2=0.001,h3=100。
3.2.2 搜索步長的確定
根據SOA搜索原理,搜索步長根據模糊系統的逼近能力,采用高斯隸屬函數[15],如

式(4)中,uA(x)是高斯隸屬度;x 是輸出變量;a、δ 是隸屬度函數的參數;根據式(4),輸出變量超出[-3δ,3δ]的概率小于0.0111,因此設定最小隸屬度值是uA=0.0111可以進行忽略。
3.2.3 搜索方向的確定
SOA的搜索方向算法是利用:個體向優秀個體進化、優秀個體向優秀群體進化、優秀群體向優秀種群進化的三個行為進行分析和建模,最終確定搜索方向。
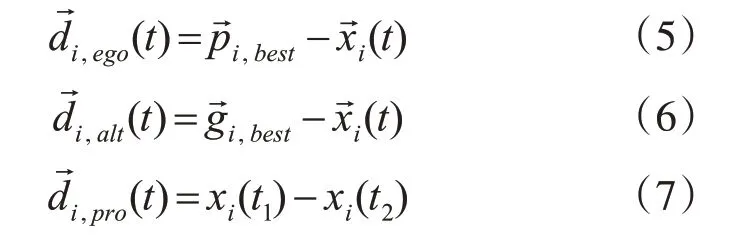
聯立上述三個公式,根據三個搜索方向的隨機加權幾何平均值確定搜索方向如式(8):
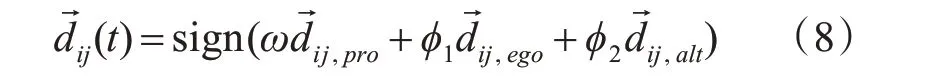
3.2.4 個體位置的更新
在確定搜索的方向和步長后,對搜索個體的位置進行更新以找到最優解。
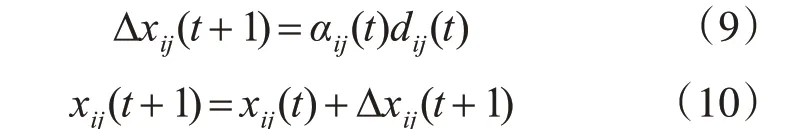
流程圖如圖2所示。
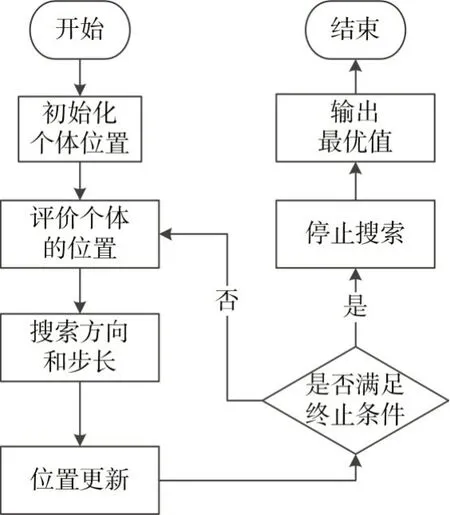
圖2 人群搜索算法SOA流程圖
4 基于人群搜索算法的直流電機傳遞函數優化設計
4.1 傳遞函數的確定
直流電動機動態數學模型的建立是獲取傳遞函數的前提[12],根據如圖3 所示的直流電動機的電樞原理圖,當控制直流電動機兩端的電壓大小為Ua時,電機的轉速為ω,時,在如圖3 中的Ra,La分別是電驅電路的電阻和電感;Ml是電動機軸上的總負載的折合阻力矩,Ma是電樞電流產生的電磁轉矩。
列舉直流電機的電壓平衡方程和轉矩平衡方程式(3),經過整理后,再進行拉普拉斯變化,帶入直流電機的各項硬件參數,可得到直流電機的傳遞函數。
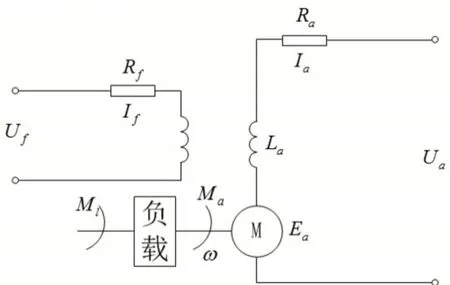
圖3 他勵直流電動機的電驅原理圖
4.1.1 列出各電網的平衡方程式
圖3 是直流電動機的工作原理等效電路圖,在該電路中有兩個子系統,一個是電網絡系統,為整個電機系統提供電能,產生電磁轉矩;另一個是機械運動系統,為負載提供轉動的動能。當電機輸出轉速為n 時,根據上述的工作原理列出如下的平衡方程式。
1)電樞網絡電壓平衡方程式
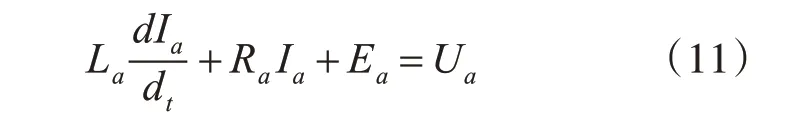
式(11)中,La是電樞電感;Ia是電樞電流;Ra分別是電樞電阻;Ea是電樞反轉時產生的電樞繞組反電動勢,它的大小與激磁磁通的大小以及轉速成正比,與電樞電量輸入量方向相反;Ua是電樞電量輸入量。
2)機械平衡方程
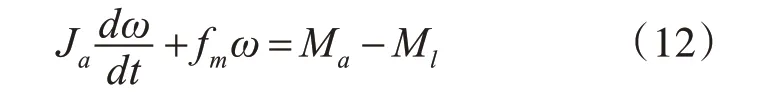
式(12)中,Ja是電動機和負載的合力在電動機軸上的轉動慣量;Ma是電樞電流所產生的電磁轉矩。
3)電磁轉矩平衡方程

式(13)中,Kc是電磁力矩常數,由電動機自身的硬件參數所確定。
4)電動勢平衡方程

式(14)中,Ke是電動勢常數,由電動機自身的硬件參數所確定;ω 是電動機的角速度。
聯立式(11)~(14),建立方程組。在實際應用中,因空載下的阻力矩和電樞的電感都很小,略去Ml,La,消除中間變量Ia,Ea,Ma得到直流電機簡化的一階微分方程式:
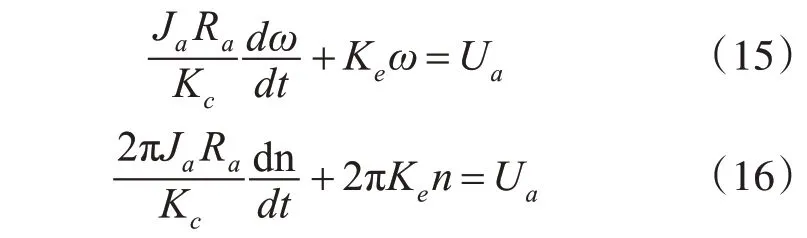
4.1.2 拉普拉斯變換
在直流電機系統中,拉普拉斯變換將系統從時域轉換到頻域,這樣做的好處是可以解決一些在時域計算復雜的問題[16]。
性質1[17]:拉普拉斯變換的常用性質
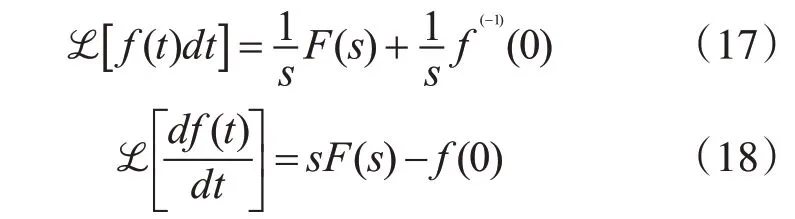
根據上述的定理,假設初始條件為零,一階導數為零,可得到直流電機的傳遞函數為
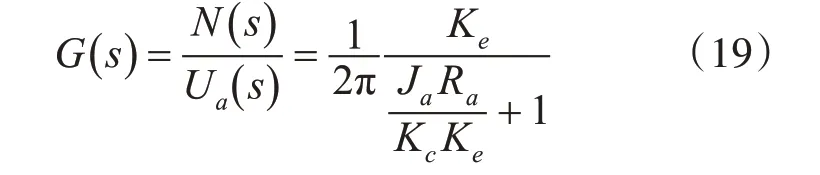
4.2 直流電機的傳遞函數
根據上述的內容可以得知直流電機的傳遞函數方程式如式(19)所示,將某型號直流電機相關的參數帶入式(19)中可得該直流電機傳遞函數為
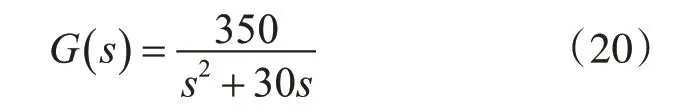
4.3 PID控制器的SOA算法優化設計
傳統上獲取PID 控制器參數方法較為繁瑣,專業性強,當系統更換直流電機時,需對PID 控制器參數重新進行整定優化。利用直流電機的機械參數快速的獲取傳遞函數,方法簡單、傳遞函數獲取簡單,獲取傳遞函數后通過SOA快速的獲取范圍內最優參數。
PID參數整定的SOA算法流程如下:
1)初始化個體的位置,為每個搜索者賦予初值;
2)根據式(2)和式(3)計算每一個個體通過搜索獲取的適應度值;
3)對每個個體位置與其個體歷史搜索獲取的最佳位置相比較,記錄個體最佳的位置;
4)對每個搜索者個體位置與其種群歷史最佳位置相比較,記錄種群最佳的位置;
5)根據式(9)和式(10),進行位置更新;
6)如果未達到結束條件,返回步驟2)循環執行,否則結束循環。
5 仿真與結果分析
5.1 控制對象及仿真條件設置
在過程控制系統中,直流電機系統通常是典型的一階或二階系統。選取上文獲取的傳遞函數如式(20)所示,分別采用傳統方法和SOA對該系統進行PID 控制器參數進行整定優化,對上述的直流電機控制系統的傳遞函數進行軟件仿真。假設種群大小為50,最大的迭代次數為100,Kp、Ki、Kd 三個參數的搜索范圍分別為0~6,0~100,0~100,輸入信號為單位階躍信號,采樣間隔時間0.001s,仿真時間10s。
5.2 仿真結果及分析
利用SOA對直流電機控制系統進行仿真,得到SOA 優化適應度函數控制曲線和系統模擬的曲線分別如圖4,圖5所示。
從圖4 優化適應度函數變化曲線進行分析,SOA在參數尋優時具有很好的收斂能力,為快速地搜索出最優參數提供了參考依據。
從圖5可以看出,Kp、Ki、Kd三個參數逐漸的收斂到一個常數。通過人群搜索算法會的系統階躍響應輸出曲線如圖6所示。
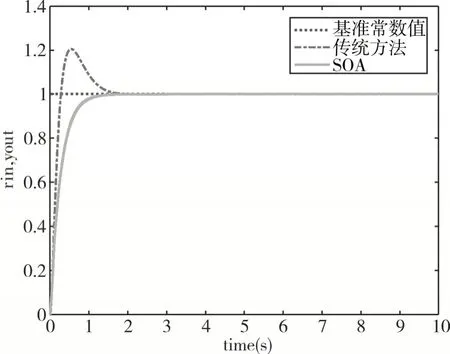
圖6 系統階躍響應輸出曲線
從圖6 的系統階躍響應輸出曲線來看,利用直流電機的各項機械參數獲取傳遞函數,通過人群搜索算法(SOA)可以快速地搜索出Kp、Ki、Kd 參數,響應時間短,使系統快速地收斂到最佳狀態。
6 結語
PID 控制器參數整定優化的結果對于直流電機的控制效果具有決定性的影響。在實際應用中,因電機的型號或者生產廠家的不同,PID 控制器之間也會存在差異,給使用者帶來不便。本文利用直流電機的各項硬件參數,結合電壓平衡方程和轉矩平衡方程式能夠準確地獲取傳遞函數,通過SOA對參數進行智能搜索以獲取種群范圍內的最優參數,從而改善了以上問題。軟件仿真結果表明,該方法可以快速獲取PID 控制器參數,為簡單、快速獲取直流電機的PID控制器參數提供參考依據。

