多維數據分析處理技術

文/藍善根

1 緒論

1.1 研究背景和意義

近年來大數據飛速發(fā)展，數據的采集技術趨于成熟，海量的數據為科技生活提供了便利，但同時數據量的龐大與繁雜為數據的計算處理與分析帶來了極大的困難，在實際生產以及生活當中，需要投入更多的研究來加強多維數據的分析與處理，使人們生產數據、處理數據、分析數據，改變科技生活，受惠于科技發(fā)展和大數據相關技術。

在數據處理當中，大部分只能分析具有某特征值的數據，當數據變成多維數據，混合屬性的時候，技術上很難分析和處理，如何高效聚類數據成為了研究的熱點。

1.2 研究現(xiàn)狀

目前對于大數據當中的數據采集技術已經有了飛速的發(fā)展和突破。數據分析方法也多種多樣，但是目前仍然存在很多問題：業(yè)務數據的采集、存儲結構多樣，形勢混亂，數量龐雜并且存在隨意亂填現(xiàn)象無效數據較多；數據分析技術不夠普及，大多數信息服務行業(yè)人員對數據的處理技術不甚了解；數據龐雜的情況下，數據分析處理的速度有限；多維數據的分析以及展示不夠智能等。

關于多維數據分析處理技術，目前有部分專家發(fā)布了較為優(yōu)秀的研究成果，如文獻［1-5］提出的各種算法以及開發(fā)出的比較先進的軟件系統(tǒng)。

1.3 本文主要內容

企業(yè)或者機構日常經營積累的額海量數據以及隨著大數據的普及，信息科技的共享展示，通過特定的手段獲取有效的信息并利用算法等科學技術挖掘數據隱含價值，指導人們在生產經營中的分析以及決策。本文主要針對多維數據分析處理技術進行了介紹以及算法仿真實驗，驗證了多維數據分析計算算法的可行性以及對計算性能的提高。

2 多維數據分析處理技術

2.1 多維數據高效聚類原理

獲取大量的多維數據信息后，采用交叉信息鏈模型來進行計算，計算結果可以獲取數據集合的離散樣本，將該樣本利用粒子群聚方法進行動態(tài)分配得到多維數據的信息素濃度，完成聚類，該過程詳細求解如下：

將海量的多維離散數據存儲在系統(tǒng)中，設數據為：

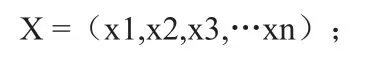
采用交叉信息鏈模型獲取數據集合中的N個樣本并將其切割得到聚類樣本Xi(i=1,2,3,…n)，矢量表示方式為：

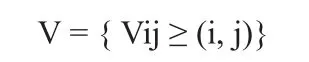
以上i取值范圍為i=1,2,3,…C，表示第i個聚類中心，Vi含義為數據結構中心的第i個矢量聚類中心，C為常數; j的取值范圍為j=1,2,3…s,表示迭代次數，s含義為帶寬頻間時間。多維離散數據Vmi的聚類劃分矩陣如下所示：

以上i取值范圍為i=1,2,3,…C，表示第i個聚類中心，k=1,2,3…n,表示n個樣本。在多維離散數據的基礎上實現(xiàn)模糊C均值聚類算法，采用群聚類算法對樣本進行動態(tài)分配來獲取信息素弄不，則表達式如下：

以上公式中，m代表權重，（dik）2含義為xk與Vi多維離散數據結構中心矢量，C代表計算機系統(tǒng)的慣性權值，代表聚類中心的非劣解，（U,V）表示非劣解的距離，采用歐式距離表達方式如下：

根據以上公式得到聚類中心最優(yōu)解如下：

結合約束條件，采用李雅普諾夫極限定理，得到聚類的中心極值為：

求解以上公式獲取聚類中心，利用以下公式進行數據聚類：

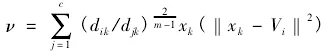
以上就是多維離散數據的高效聚類原理，通過該過程完成數據的聚類。

2.2 多維離散數據高效聚類方法

在2.1的基礎原理上，利用離散性時間序列分析方法構建目標函數，得到最優(yōu)聚類中心，采用優(yōu)化算法對最優(yōu)聚類中心進行優(yōu)化，就是本文要實現(xiàn)的高效聚類方法。

首先，構建多維離散數據信息流模型，提取其時延尺度特征值，以此構建多維離散數據目標函數，求解該函數得到最優(yōu)聚類中心，操作過程如下所示：

構造多維離散數據變量時間序列{Xn}，樣本長度取值為n，設樣本數據流分類特征屬性為X、Y，最小嵌入為數為m，最優(yōu)延遲為τ，當數據特征的平均速度得到滿足時，信息流模型為：

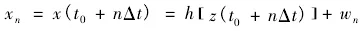
以上公式中，n為樣本長度，t0為聚類中心檢索，△t為單位時間變化，h為數據時間序列中每個樣本獨立的相似性特征量，為時延尺度。根據計算多維離散數據關聯(lián)度來表示數據離散性時間序列的特征，并進行空間重構，得到時間序列分布軌跡如下：

表1：不同聚類方法用時對比

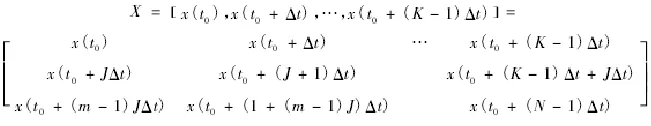
以上x(t)為采集樣本的時間，J為多維離散數據相關系數，△t表示抽樣時間間隔，m表示嵌入維數，可以用K=N-（m-1）*J來表達時間序列分類的最大屬性，得到向量模型以及特征空間數據矢量如下所示：

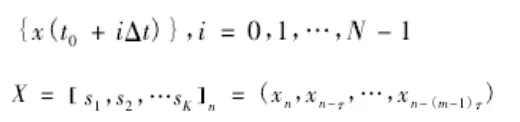
以上公式構造了海量數據流提取特征值屬性，根據以上成果構建目標函數，數據的分布模型如下所示：

以上公式中，a0為數據采樣初始值，xn-1代表數值相同的時間序列，bi為最佳分類屬性，設多維離散數據時間標函數為x(t)（t=0,1,2…n-1），采用2.1提到的模糊均值聚類算法搜索有限的數據集向量如下：

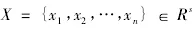
將數據集向量按照屬性分類，得到n個數據樣本數量，用xi（i=1,2,3…n）表示多維離散數據信息增益矢量如下：

在以上多維離散數據信息增益矢量的數據集中選K個實例，則其目標函數最優(yōu)聚類中心得以求解，用公式表示為：

得到多維離散數據的最優(yōu)聚類中心以后，其次要利用優(yōu)化算法對最優(yōu)聚類結果進行優(yōu)化從而實現(xiàn)高效聚類。具體優(yōu)化過程如下所示：

第一步，用α和β編碼每個聚類中心，要求α和β滿足 |α|2+|β|2=1，觀測并生成二進制的普通種群，假設量子種群為 pop，數據集類別為 K，數據維數為 D，每一個維數用b位二進制來表示，則每一個量子染色體的長度 L= K×D×b。則種群 Q(t) = {qt1，qt2，…，qtpop}中第 i 個個體的編碼形式為：

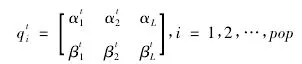
代入t=0來對量子集合進行初始化并觀測結果，獲取普通的種群如下：

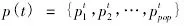
估計普通種群p（t）并計算出每個個體的適應度，提取適應度最大的個體：

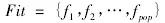
修正Q（t）形成新生集合：

利用以上公式擾動抑制聚類中心從而實現(xiàn)對多維離散數據的優(yōu)化：

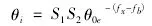
2.3 仿真實驗以及結果分析

2.1以及2.2介紹了該算法的原理以及計算方法，本小節(jié)將對其進行仿真實驗，文獻[6]以及文獻[7]分別介紹了另外兩種不同的處理方法，下面我們將仿真實驗結果與另外兩種算法實驗結果進行對比。對比結果中，Q值的結果如下圖1所示。

圖1為文獻[6]的聚類方法結果與本文提到的聚類方法對比，不端的加大聚類參數個數，Q值隨之不同幅度增大，通過圖1中對比可知，本文方法在效率和性能方面優(yōu)于之前的算法。

單一的對比具有局限性，為了更好的對比不同的算法，本文又采取了讓文獻[7]的方法進行計算，將本文、文獻[6]、文獻[7]的三種方法計算時間的結果進行對比，對比結果如表1所示。

由表1結果對比可知，隨著需要計算的數據點個數不斷加大，計算時間不同的同時，計算時間變化有不同程度的增幅。本文提到的算法明顯優(yōu)于其他兩種早期提出的算法，有效的提高了計算效率。

3 結論

本文研究了早期的一些聚類方法，發(fā)現(xiàn)其計算效率較差。因而提出了另一種優(yōu)化算法，提高當前大數據前提下多維離散數據的計算方法，實驗結果證明該方法可行并且優(yōu)于早期的一些計算方法。該方法雖然有效提高了數據計算的效率，但是仍存在一些不足，希望更多的研究者們提出更優(yōu)化、更效率的多維離散數據計算方法。大數據正在普及，數據的存儲計算以及展示優(yōu)化在未來一定迎來更廣闊的發(fā)展。

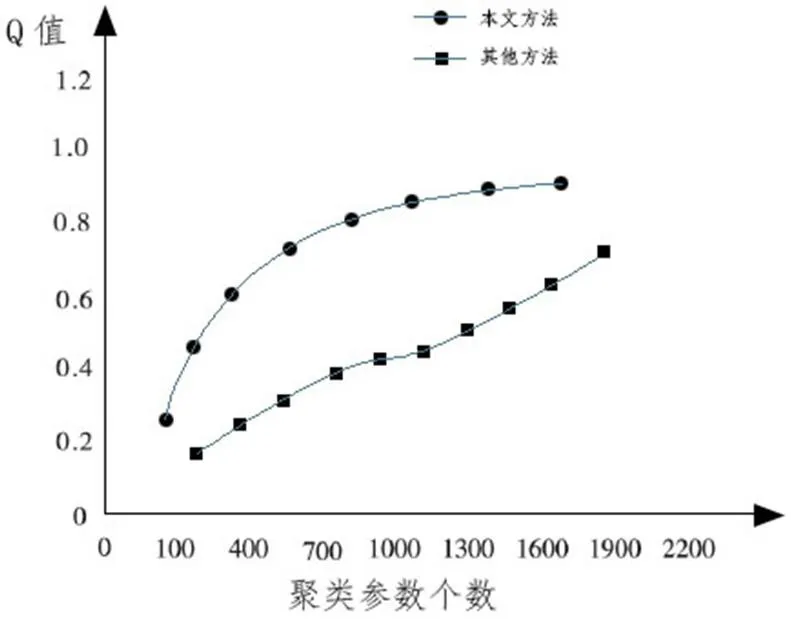
圖1：不同聚類方法Q值對比