基于雙層復雜網絡的城市交通網絡協同優化方法

陳曉明 李引珍 沈 強 巨玉祥

摘 要：針對城市交通網絡中旅客在公共交通出行路徑選擇時面臨的地鐵與公交雙層網絡在換乘銜接協同中存在的部分換乘站點之間距離過遠、銜接導向不明確、局部換乘供需不平衡等問題，提出基于雙層復雜網絡的城市交通網絡協同優化方法。首先，采用邏輯網絡拓撲方法對城市交通網絡進行拓撲，并基于復雜網絡理論建立地鐵公交雙層網絡模型。然后，以換乘車站為研究對象，提出一種基于K-shell分解法和中心性權重分配的節點重要度評價方法，對大規模網絡中的地鐵、公交車站進行粗粒度和細粒度劃分和識別，并在此基礎上提出一種相互激勵的雙層城市交通網絡協同優化方法，即在雙層網絡結構優化中引入復雜網絡理論中對于網絡拓撲中節點重要度的識別和篩選方法，通過對路徑選擇中高集聚效應的識別和有利節點的定位更新雙層網絡結構以優化現有網絡的車站布局和銜接關系。最后，將提出的方法應用于成都市地鐵公交網絡，優化了現有網絡結構，得到了現有網絡的最佳優化節點位置和優化數量，并且通過相關指標系統驗證了該方法的有效性。

實驗結果表明，采用該方法優化32次后的網絡全局效率達到最優，和平均最短路徑的優化效果分別為15.89%、16.97%，旅客換乘行為提升57.44個百分點;

優化方法對旅行成本在8000～12000m的可達性影響最明顯，優化效果平均達到23.44%;同時引入雙層網絡速度比和單位交通成本比，突出了不同運營狀況下交通網絡對協同優化過程的反應和敏感度的不同。

關鍵詞： 城市交通網絡;雙層復雜網絡;協同優化;節點評價;協作強度

中圖分類號：TP393.02

文獻標志碼：A

Abstract：? In order to solve the problems in the transfer process connection and collaboration of metro-bus two-layered network faced by the passengers making route selection in the urban transportation network， such as the far distance between some transfer stations， the unclear connection orientation and the imbalance betweensupply and demand in local transfer?a collaborative optimization method for urban traffic networks based on two-layered complex networks was presented. Firstly， the logical network topology method was applied to the topology of the urban transportation network， and the metro-bus two-layered network model was established by the complex network theory. Secondly， with the transfer station as research object， a node importance evaluation method based on K-shell decomposition method and central weight distribution was presented. This method was able to realize coarse and fine-grained divison and identification of metro and bus stations in large-scale networks. And a collaborative optimization method for two-layered urban traffic network with mutual encouragement was presented， that is to say the method in the complex network theory to identify and filter the node importance in network topology was introduced to the two-layered network structure optimization. The two-layered network structure was updated by identifying high-aggregation effects and locating favorable nodes in the route selection to optimize the layout and connection of stations in the existing network. Finally， the method was applied to the Chengdu metro-bus network， the existing network structure was optimized to obtain the optimal optimized node location and number of existing network， and the effectiveness of the method was verified by the relevant index system.The results show that the global efficiency of the network is optimized after 32 optimizations， and the optimization effect of the average shortest path is 15.89% and 16.97%， respectively， and the passenger transfer behavior is increased by 57.44 percentage points，the impact on the accessibility is the most obvious when the travel cost is 8000-12000m with the optimization effect of 23.44% on average. At the same time， with the two-layered network speed ratio and unit transportation cost introduced， the response and sensitivity difference of the traffic network to the collaborative optimization process under different operational conditions are highlighted.Key words：? urban transportation network; two-layered complex network; cooperative optimization; node evaluation; cooperative strength

0 引言

城市軌道交通與常規公交網絡在配合和銜接上的合理優化，能夠實現公共交通系統的高效協同。在對城市軌道交通和常規公交的協同優化研究方法中，文獻[1]通過確定軌道交通及其接運公交線路的發車頻率，以總費用最小為目標，使一條軌道交通線與多條常規公交線協調運營，主要以優化銜接線路為手段提高軌道交通與常規公交之間的協同，但是未從網絡結構的角度優化兩者的協同，導致優化效果具有局限性。文獻[2-6]研究了交通網絡的復雜性特征，復雜系統結構與功能之間的關系問題是復雜網絡研究中的一個核心問題[3]。網絡結構對于網絡傳輸具有重要的影響[4]，因此優化網絡結構、改善系統功能引起了復雜網絡領域許多學者的關注[5]。節點及節點間的相互關系構成了復雜網絡，決定了網絡特性[6]。文獻[7]通過對

19世紀到20世紀

的倫敦人口、土地利用和交通網絡的研究，驗證了三者關系符合協同優化模型，發現人口密度和網絡密度是正相關的，并指出這種協同優化是一個具有互動性的反復過程。文獻[8]以北京市的路網擴張與交通增長為對象，提出了一個協同優化模型，對其進行穩定性分析和數值模擬，揭示了人流、車流以及路網之間的相互作用。上述研究在研究交通網絡協同優化時只考慮了單層網絡情況，而實際中交通網絡系統具有包含多種交通方式的多層屬性，網絡節點之間的交通流與多個層面有關。對此，文獻[9]基于雙層復雜網絡理論建立多模式交通流動態模型，分析了雙層交通網絡中換乘擁堵的形成原因，并就擁堵的生滅過程和規模提出了計算方法。文獻[10]為了描述雙層網絡之間合作的涌現，建立模型并引入了協作強度的概念以闡明耦合網絡的關系，并通過歐洲和中國的鐵路航空雙層網絡進行實證研究。文獻[11]以城市道路網絡和地鐵網絡為研究對象，分析了城市交通網絡基于最短路徑（Shortest Path Length， SPL）變化的多層結構影響，并找到了最佳結構。這些研究引入了多層網絡模型來分析不同交通模式的相互合作關系，但沒有提出如何利用雙層網絡之間的合作關系提出明確的方法來改進網絡結構。文獻[12]提出了一個城市交通網絡多層優化方法，選擇隨機向地鐵網絡增加車站，以期達到理想的協同效果，但這種方法存在很大程度上的盲目性，缺乏實際意義。

在城市交通網絡系統中，制約網絡全局運輸效率和能力的往往是地鐵和常規公交換乘車站協同的優劣，分析站點之間不能很好地換乘協同的原因主要有：常規公交距離地鐵出入口距離過遠;換乘需求大的公交線路未出現在鄰近地鐵站點;地鐵站點與公交樞紐缺少直連通道或換乘路徑存在物理障礙。文獻[13]結合城市軌道交通車站客流及其網絡拓撲度，研究了城市軌道交通車站重要度，研究發現重要度高的車站均為換乘車站。

針對上述問題，本文提出一種基于雙層復雜網絡節點重要度的城市交通網絡協同優化方法——基于雙層復雜網絡的城市交通網絡協同優化方法。

該方法通過節點重要度識別，在重要的公交網絡節點位置添加新的軌道交通節點與其形成換乘關系， 一方面通過改進網絡拓撲結構提高節點可達性， 另一方面通過提高地鐵公交換乘率，從路徑選擇上緩解集聚效應高的節點承載壓力。

將網絡平均最短路徑、網絡全局效率、雙層網絡協作強度、優化網絡與原始網絡總交通成本之比、網絡可達性作為評價指標，驗證雙層網絡協同優化方法合理性。在此基礎上，建立基于地鐵公交雙層網絡協同優化模型，研究雙層網絡協作強度與上下兩層速度比關系以及旅客出行方式選擇與不同層的單位交通成本關系。

1 理論與模型

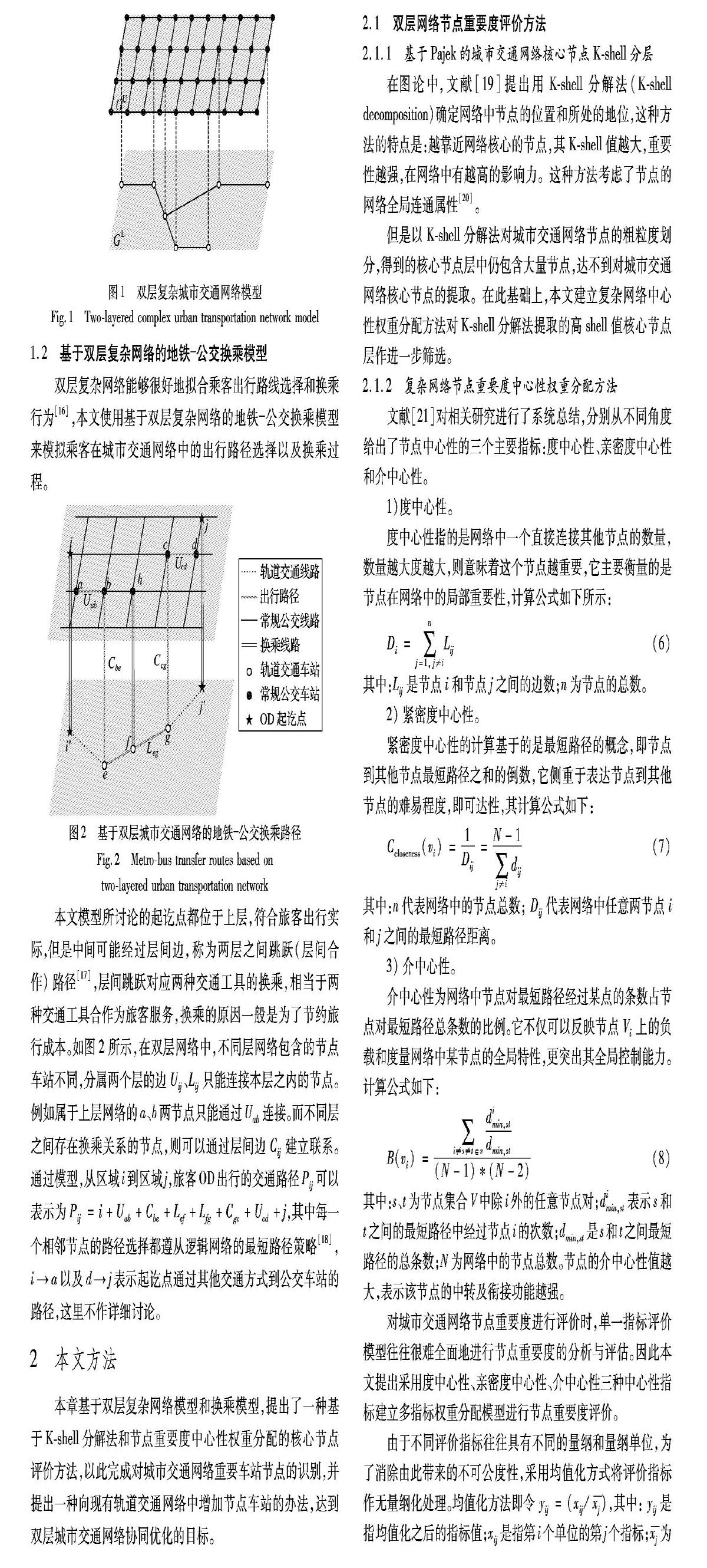
1.1 城市交通雙層網絡模型

多層表示方法被定義為M空間（M-space）模型[12]，類似于最初由文獻[14]提出的L空間（L-space）和P空間（P-space）模型。本文基于BA模型[15]和M空間模型將城市公共交通系統作為一個多層網絡，采用復雜雙層網絡理論來表示城市軌道交通和常規公交網絡，以區分不同層網絡間的異質性。該系統內所有車站抽象為節點的集合，車站之間的區間抽象為節點之間的連接邊的集合，利用數學模型來描述由車站和線路構成的網絡拓撲結構，用于全面分析城市交通網絡的性能，數學模型描述如下：

1.2 基于雙層復雜網絡的地鐵公交換乘模型

雙層復雜網絡能夠很好地擬合乘客出行路線選擇和換乘行為[16]，本文使用基于雙層復雜網絡的地鐵公交換乘模型來模擬乘客在城市交通網絡中的出行路徑選擇以及換乘過程。

2 本文方法

本章基于雙層復雜網絡模型和換乘模型，提出了一種基于K-shell分解法和節點重要度中心性權重分配的核心節點評價方法，以此完成對城市交通網絡重要車站節點的識別，并提出一種向現有軌道交通網絡中增加節點車站的辦法，達到雙層城市交通網絡協同優化的目標。

2.1 雙層網絡節點重要度評價方法

2.1.1 基于Pajek的城市交通網絡核心節點K-shell分層在圖論中，文獻[19]提出用K-shell分解法（K-shell decomposition）確定網絡中節點的位置和所處的地位，這種方法的特點是：越靠近網絡核心的節點，其K-shell值越大，重要性越強，在網絡中有越高的影響力。這種方法考慮了節點的網絡全局連通屬性[20]。

但是以K-shell分解法對城市交通網絡節點的粗粒度劃分，得到的核心節點層中仍包含大量節點，達不到對城市交通網絡核心節點的提取。在此基礎上，本文建立復雜網絡中心性權重分配方法對K-shell分解法提取的高shell值核心節點層作進一步篩選。

2.1.2 復雜網絡節點重要度中心性權重分配方法文獻[21]對相關研究進行了系統總結，分別從不同角度給出了節點中心性的三個主要指標：度中心性、親密度中心性和介中心性。

度中心性指的是網絡中一個直接連接其他節點的數量，數量越大度越大，則意味著這個節點越重要，它主要衡量的是節點在網絡中的局部重要性，計算公式如下所示：

其中：Lij是節點i和節點j之間的邊數;n為節點的總數。

2）緊密度中心性。

緊密度中心性的計算基于的是最短路徑的概念，即節點到其他節點最短路徑之和的倒數，它側重于表達節點到其他節點的難易程度，即可達性，其計算公式如下：

其中：n代表網絡中的節點總數; Dij代表網絡中任意兩節點i和j之間的最短路徑距離。

3）介中心性。

介中心性為網絡中節點對最短路徑經過某點的條數占節點對最短路徑總條數的比例。它不僅可以反映節點Vi上的負載和度量網絡中某節點的全局特性，更突出其全局控制能力。計算公式如下：

其中：s、t為節點集合V中除i外的任意節點對;dimin，st表示s和t之間的最短路徑中經過節點i的次數;dmin，st是s和t之間最短路徑的總條數;N為網絡中的節點總數。節點的介中心性值越大，表示該節點的中轉及銜接功能越強。

對城市交通網絡節點重要度進行評價時，單一指標評價模型往往很難全面地進行節點重要度的分析與評估。因此本文提出采用度中心性、親密度中心性、介中心性三種中心性指標建立多指標權重分配模型進行節點重要度評價。

由于不同評價指標往往具有不同的量綱和量綱單位，為了消除由此帶來的不可公度性，采用均值化方式將評價指標作無量綱化處理。均值化方法即令 yij=（xij/xj），其中： yij是指均值化之后的指標值;xij是指第i個單位的第j個指標;xj為指標j的均值。

綜上，提出網絡中心性權重分配的節點重要度公式如下：

其中：BC（Between and Centrality）稱為節點i的介親密度中心性;α、 β、γ分別表示度中心性、親密度中心性、介中心性三種中心性指標的權重。為了減少權重確立時主觀因素的影響，本文基于熵權法原理，以成都市地鐵網絡139個節點車站的原始數據為基礎，采用信息熵確立評價模型中各個子指標的權重。最后，計算得到最終的α、 β、γ值分別為0.248、0.096、0.656。

2.2 雙層網絡節點更新方法

城市交通雙層網絡協同進化方法基于常規公交網絡和城市軌道交通網絡換乘協作特性，首先通過分別對兩個網絡進行節點重要度的判定，實現對軌道交通高負載節點以及現有公交網絡中適合建立軌道交通車站節點的有利節點識別和篩選的目標，在此基礎上對軌道交通新節點進行定位，從而產生新的城市軌道交通網絡。

2.2.1 城市交通雙層網絡協同優化方法

協同進化的重點目標是緩解換乘任務重的軌道交通車站的客流壓力，而城市軌道交通高負荷的節點一般出現在多線換乘、地面公交樞紐、連接方向多、換乘任務重的車站節點。故本文提出基于節點車站重要度評估的協同進化方法，具體步驟如下：

首先按BC值由高到低依次判斷，若上層網絡的核心節點已存在于既有軌道交通車站節點的服務半徑（R）內，如圖3（b）所示，公交車站（g）與軌道交通車站（c）存在換乘關系，受軌道交通線路站間距限制c處將不能作進一步處理;若上層核心節點（h）不存在于任意的軌道交通站點服務半徑（R）內，但該節點空間位置對應于下層網絡既有線路，新的有利節點（nadd）將定位于下層網絡中符合服務半徑限制L（nold-nadd）≥R的位置（hadd）。若不存在既有線路（k），則nadd直接定位于下層網絡中上層核心節點對應的位置（kadd）。

若有利節點定位均存在于既有下層網絡軌道交通節點服務半徑內 ，L（nadd-nold

這種方法針對換乘節點之間影響雙層網絡協同的原因，以優化目標在整個網絡中的地位作為主要判斷依據，首先保證了優化節點一定在最高的K-shell層中，其次在此集群中以中心性權重分配方法對核心節點的重要性再評估，同時考慮了城市軌道交通網絡節點的整體和局部特性，能夠更為全面地評價節點重要性，保證了加入的優化節點對于提高網絡性能有明顯作用。

2.2.2 網絡協同進化評價與分析

為了驗證本文提出的基于雙層復雜網絡的城市交通網絡協同進化方法的合理性，引入多種指標[12]以反映協同進化后加入新的有利節點對于網絡全局的影響。

2.3 模型的假設

本文模型基于以下假設：

1）基于成都市城市軌道交通網絡定義平均軌道交通服務半徑950m。

2）Cij取288，對于軌道交通內部k線交叉的換乘車站，將其虛擬成k個分布在各自線路上的節點，虛擬節點之間通過實際換乘距離連接[22]，其中內部換乘距離取213.5。

3）網絡內乘客的出行路線選擇使用最短加權路徑遍歷網絡，使用加權網絡的鄰接矩陣，利用Matlab軟件編程進行Dijkstra算法搜索，得到任意OD之間的最短距離。

3 案例分析

利用成都市地鐵與常規公交網絡進行模型實證。據統計，截止到2018年3月，成都地鐵共運營線路6條，車站139座，運營總里程196.47km，年工作日均客運量達214萬人次。同時，成都市共有公交線路591條，公交站點5726個，日均載客量475萬人次。

由于公交站點數量龐大，基于本文研究特性，首先通過軌道交通服務半徑為約束進行篩選，將成都市市區三環內公交網絡按照950m的平均服務半徑均等劃分為330個區域，對于每一個區域中存在地鐵站點的隨機選取其服務半徑內的一個公交站點，區域內沒有地鐵站點本文隨機選取一個公交站點來代表該區域。同時將具有相同站點名稱的常規公交車站視為同一站點，忽略其具體停靠位置的差異。

3.1 基于雙層復雜網絡的城市交通網絡協同進化方法

根據定義及統計的成都市地鐵、公交線路及站點坐標信息，建立成都城市交通雙層網絡的鄰接矩陣。根據2.2.1節提出的協同進化方法，采用Pajek軟件對成都地鐵、公交網絡進行K-shell分解，所得結果如表1所示，K-shell分解法將地鐵網絡分為5層、公交網絡分為14層。表2是成都市地鐵、公交網絡K-shell值最高的前10個車站。

然后基于協同優化方法，在軌道交通網絡定位優化節點的位置。在第一次優化中，使用K-shell分解法與中心性權重分配方法對成都市地鐵公交雙層網絡中的節點完成識別后，發現在成都公交網絡BC值排名前10的站點中二環三友路口、火車北站西、二環牛市口、火車北站、紅牌樓東、萬年場、一環路南二段已處于現有軌道交通網絡車站節點的服務半徑中，因此放棄這些位置，新的軌道交通節點將首先定位于二環桃溪路口車站，根據協同優化方法，與其建立換乘關系，并接入現有軌道交通網絡中。此時，整個城市交通網絡完成第一次協同優化，然后對這一過程進行評價與分析。

3.2 協同優化過程評價與分析

首先通過Dijkstra算法得到進化之前成都公交雙層網絡的OD最短路徑矩陣，使用Matlab計算得到原始成都市雙層網絡APL為9759.5m，E（G）為1.514E-04，在雙層網絡219961條OD路徑中，總共有14119條線路是使用了地鐵換乘，此時協作強度Λ為0.0081，而第一次進化后APL為9341.6m，E（G）為1.526E-04，有28775條換乘路徑，Λ為0.0094。

本文總共對成都市地鐵公交雙層網絡進行50次循環的協同優化，表4是網絡優化過程中部分新節點的定位和接入關系，并最終得到了每次進化前網絡同優化之后網絡的明確關系。

從圖4（a）可以看出，對于地鐵公交雙層網絡，協同優化過程增加50個節點對APL有很大影響，尤其當增加32個車站時，多層網絡APL急劇下降16.97%。可以發現地鐵車站節點的增加，對于APL的影響總是積極的，但在優化后期，優化效果開始減弱。如圖4（b）所示，雙層網絡的E（G）先增加了15.89%達到峰值，然后呈現逐漸下降的趨勢。反映出在有限且有序的城市交通網絡內，無限制地增加地鐵車站節點反而會降低網絡全局效率。以上兩個指標反映了協同優化過程對雙層網絡結構的特征和影響的一致性，除此之外，必須考慮雙層網絡的耦合協作特征。

如圖5（a）所示，在雙層網絡協同優化過程中，雙層網絡協作強度Λ隨著平均最短路徑的減小而增大，這表明了APL的減小是由于更多的旅客選擇了換乘，如圖6（b）所示。

以上結果顯示了在換乘路徑的持續增長帶來APL減小的影響下，Λ呈現不斷增大的變化趨勢。但是這種基于最短路徑的旅客換乘行為忽略了雙層網絡不同交通模式之間存在的交通成本差異，增加了網絡節點，大部分OD最短路徑長度SPL將改變，同時經由SPL的總交通成本也會發生變化，通過Ψ表示的旅客選擇換乘的行為也會改變，并且通過協同優化過程可以發現一個變化的趨勢。

以上變化表明了在雙層網絡協同進化過程中，起初Ψ隨著雙層網絡總最短路徑∑i≠j（SPL）ij急劇減小而迅速降低，更多的旅客選擇換乘城市軌道交通，以降低旅行成本。但隨著軌道交通節點的不斷加入，∑i≠j（SPL）ij的減小速度開始放緩，而且換乘路徑在所有路徑選擇中所占的比例越來越大，例如在最后20次優化中，∑i≠j（SPL）ij僅減小約6%，而換乘路徑比例增加了約15%，考慮到不同層單位總交通成本的差異，∑i≠j（SPL）ij經由下層網絡的總交通成本持續增長。此時當增加軌道車站節點所帶來的∑i≠j（SPL）ij的減小不足以抵抗交通總成本的增長時，此時Ψ值隨迭代次數增加。這也表明Ψ值與公交地鐵雙層旅行成本之比（ωsτs/ωrτr）具有密切關系，而ωsτs/ωrτr的變化總是伴隨著當地經濟城市發展或當地交通現狀的不同需求，在不同的城市可能會有所不同。如圖7所示是在網絡優化過程中，基于不同ωsτs/ωrτr值的Ψ變化情況，當ωsτs/ωrτr=0.1時，增加50個地鐵節點Ψ值上升近170%，旅客不會選擇換乘地鐵出行，但這種情況較為極端，旅行成本差異在兩種公共交通出行方式上不會這么明顯。當ωsτs/ωrτr的值處于0.5～1時，Ψ值總體趨于相對穩定。但當ωsτs/ωrτr=2時，增加地鐵車站會使Ψ值隨迭代次數急劇減小，此時更多的旅客將選擇換乘地鐵出行。這種情況會出現在地面交通擁堵系數和通行能力或其他因素導致常規公交網絡單位旅行成本明顯高于地鐵網絡的城市。

考慮到雙層網絡交通模式的差異，協作強度不但與網絡結構相關，同時與上下兩層網絡的速度比Θ有關。如圖5（b）所示，在上下兩層網絡結構不變的情況下，協作強度Λ（θ）隨著Θ的增加而增加。它們之間的相互關系是：Λ（θ）反映了由城市交通路網布局和交通運營狀況決定的最短加權路徑所表現的用戶行為，Θ反映的是用于調整路網功能布局的不同網絡運行規則和策略，優化次數反映的是網絡結構的調整變化。為分析優化次數和Θ對Λ影響程度，作靈敏度分析如圖8所示，Λ和Θ的關系表明當上下兩層網絡速度差異過大時，旅客在考慮總交通成本的基礎上會選擇使用速度高的單一交通模式出行，網絡結構變化對于旅客出行方式的選擇影響微弱，雙層網絡協作強度也較低;而當兩層速度比接近1時，協作強度急劇上升，旅客會在基于最短路徑的策略基礎上選擇使用雙層交通網絡模式出行，此時網絡結構的變化會對旅客出行策略產生較大影響。因此，協作強度Λ對于雙層網絡速度比Θ比優化次數更敏感

4 結語

城市交通網絡的多層表示可以說明和解釋地鐵和公交網絡兩個層面的相互協作和影響，本文引入雙層復雜網絡理論來表示城市地鐵公交雙層交通網絡，考慮到影響雙層網絡之間不能高效協同的原因，建立了基于K-shell分解法和復雜網絡中心性多指標權重分配方法的地鐵公交雙層網絡協同優化模型。通過成都市地鐵公交網絡進行模型驗證，當下層網絡獲得固定數量的節點時，Ψ值達到最低值，并且在不同的旅行成本下，Ψ和優化節點數量間有正相關和負相關的關系。Λ和Θ有正相關關系，協同優化對Λ和APL有積極作用，而E（G）在這一過程中有最佳點。分析了協同優化對于可達性的最佳影響的旅行范圍。結果表明，通過利用當前的網絡特征和旅客的行為變化來確定當前網絡規模下的最佳優化節點及優化數量，可以達到合理的網絡結構從而提高整個網絡的性能。城市公共交通網絡協作強度與不同層運行速度高度相關，現有網絡也可以依賴這些指標更好地運行，而這決定于不同城市的交通布局和交通運營現狀。本文的研究也為城市軌道交通網絡的改進及新線規劃提供思路，同時本文的協同優化方法也可以衍用到多層面的多模式交通網絡結構優化中。

本文的優化過程僅強調了地鐵公交協同下軌道交通的增長，需要更多的數據進一步考慮城市地面交通、土地擴張、人口增長等因素來完善優化過程。此外，本文現階段針對網絡靜態的拓撲結構的優化研究，需進一步考慮加載動態客流之后對于雙層網絡的協同優化影響。

參考文獻（References）

[1] CHIEN S， SCHONFELD P. Joint optimization of a rail transit line and its feeder bus system[J]. Journal of Advanced Transportation， 1998， 32（3）： 253-284.

[2] ZHANG J， ZHAO M， LIU H， et al. Networked characteristics of the urban rail transit networks[J]. Physica A： Statistical Mechanics & Its Applications， 2013， 392（6）： 1538-1546.

[3] 李明高， 杜鵬， 朱宇婷， 等. 城市軌道交通換乘節點與網絡運行效率關系研究[J]. 交通運輸系統工程與信息， 2015， 15（2）： 48-53. （LI M G， DU P， ZHU Y T， et al. Effect of urban rail transit transfer nodes on network performance[J]. Journal of Transportation Systems Engineering and Information Technology， 2015， 15（2）： 48-53.）

[4] CARMI S， WU Z， HAVLIN S， et al. Transport in networks with multiple sources and sinks[J]. Europhysics Letters， 2008， 84（84）： 28005.

[5] XUE Y， WANG J， LI L， et al. Optimizing transport efficiency on scale-free networks through assortative or dissortative topology[J]. Physical Review E — Statistical， Nonlinear， & Soft Matter Physics， 2010， 81（3）： 37101.

[6] GAO C， WEI D， HU Y， et al. A modified evidential methodology of identifying influential nodes in weighted networks[J]. Physica A： Statistical Mechanics & Its Applications， 2013， 392（21）： 5490-5500.

[7] LEVINSON D. Density and dispersion： the co-development of land use and rail in London[J]. Journal of Economic Geography， 2007， 8（1）： 55-77.

[8] WU J， XU M， GAO Z. Modeling the coevolution of Road expansion and urban traffic growth[J]. Advances in Complex Systems， 2014， 17（1）： 1450005.

[9] SOL-RIBALTA A， GMEZ S， ARENAS A. Congestion induced by the structure of multiplex networks[J]. Physical Review Letters， 2016， 116（10）：108701.

[10] GU C， ZOU S， XU X， et al. Onset of cooperation between layered networks[J]. Physical Review E — Statistical， Nonlinear & Soft Matter Physics， 2011， 84（2）： 026101.

[11] STRANO E， SHAI S， DOBSON S， et al. Multiplex networks in metropolitan areas： generic features and local effects[J]. Journal of the Royal Society Interface， 2015， 12（111）： 20150651.

[12] DING R， UJANG N， HAMID H B， et al. Heuristic urban transportation network design method， a multilayer coevolution approach[J]. Physica A： Statistical Mechanics & Its Applications， 2017， 479： 71-83.

[13] JIN J， LI M， WANG Y， et al. Importance analysis of urban rail transit network station based on passenger[J]. Journal of Intelligent Learning Systems and Applications， 2013， 5（4）： 232-236.

[14] PORTA S， CRUCITTI P， LATORA V. The network analysis of urban streets： a dual approach[J]. Physica A： Statistical Mechanics & Its Applications， 2006， 33（2）： 853-866.

[15] BARABáSI A， ALBERT R. Emergence of scaling in random networks[J]. Science， 1999， 286（5439）： 509-512.

[16] MORRIS R G， BARTHELEMY M. Transport on coupled spatial networks[J]. Physical Review Letters， 2012， 109（12）： 128703.

[17] 李凱軍， 顧長貴， 瞿艷青， 等. 一些實際雙層網絡之間的合作涌現[J]. 復雜系統與復雜性科學， 2012， 9（2）： 79-83. （LI K J， GU C G， QU Y Q， et al. Onset of cooperation in some real world layered networks[J]. Complex Systems & ComplexityScience， 2012， 9（2）： 79-83.）

[18] NIAN X， FU H. Efficient routing on two layer degree-coupled networks[J]. Physica A： Statistical Mechanics & Its Applications， 2014， 410： 421-427.

[19] KITSAK M， GALLOS L K， HAVLIN S， et al. Identification of influential spreaders in complex networks[J]. Nature Physics， 2010， 6（11）： 888-893.

[20] 王小俊， 王彬， 夏一丹， 等. 基于介中心性及K-shell的腦網絡核心節點評價方法[J]. 計算機工程與應用， 2017， 53（11）： 44-49. （WANG X J， WANG B， XIA Y D， et al. Evaluation method of node centrality for brain network based on betweenness centrality and K-shell[J]. Computer Engineering and Applications， 2017， 53（11）： 44-49.）

[21] FREEMAN L C. Social Network Visualization， Methods of[M]// MEYERS R. Computational Complexity. New York： Springer， 2009： 2981-2998.

[22] 陳培文， 陳峰， 胡映月， 等. 基于復雜網絡的城市軌道交通網絡中心性研究[J]. 復雜系統與復雜性科學， 2017， 14（2）： 97-102， 109. （CHEN P W， CHEN F， HU Y Y， et al. On urban rail transit network centrality using complex network theory[J]. Complex Systems & Complexity Science， 2017， 14（2）： 97-102， 109.）