雙關節機械手最優軌跡控制算法優化

文/趙連娟

常見工業機器人就是利用對于機械手中的伺服電機進行控制，準確控制機械手自由端運行軌跡，常見類型有：直接坐標型、圓柱坐標型、球坐標型和關節型。如圖1所示，關節型機械手運行軌跡通過極坐標來研究。關節式機械手是一種適用于靠近機體操作的傳動形式。它由仿生學設計而來，可實現多個自由度自由連接，動作靈活，適于在狹窄空間工作。在本文中主要研究關節型機械手的控制算法優化問題。

圖1：機械手主要類型

1 控制現狀

工業機械手在運行中就會面臨著抖動，而抖動會增加額外的能量輸出從而引起軌跡變化。工業機械手的軌跡規劃主要有兩種：一種是對機械手的路徑軌跡規劃，另一種是對機械手運動過程中的位移、速度以及加速度的曲線輪廓規劃。

對于多關節機械手來說，運行軌跡是不固定的，所以可以從運行軌跡分析系統，也能從能量角度上減少能量損失，對其速度、加速度進行算法優化控制。在傳統控制過程中，一般采取普通差分算法，通過樣條插值逐漸逼近控制最優參數。

2 算法優化方法

由于簡單的三次樣條函數差值優化算法會產生抖動，規劃曲線不夠平滑，所以要對原算法進行優化。對于雙關節機械手每一關節的擺線運動學方程表達式描述如式（1）：

對運行軌跡離散化，對其進行采樣，采樣時間選擇為

圖2：理想軌跡、最優軌跡及軌跡跟蹤

圖3：控制輸入信號

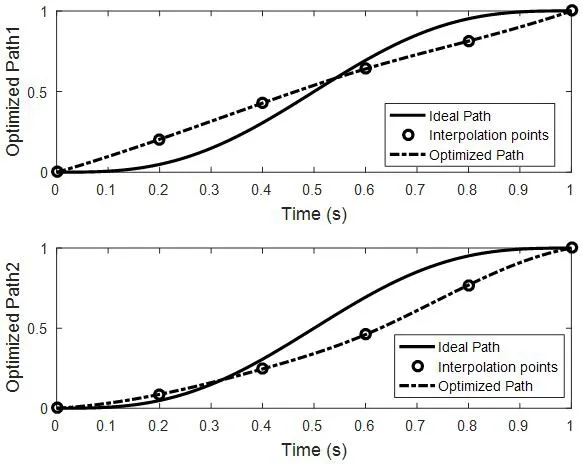
圖4：最優軌跡的優化效果

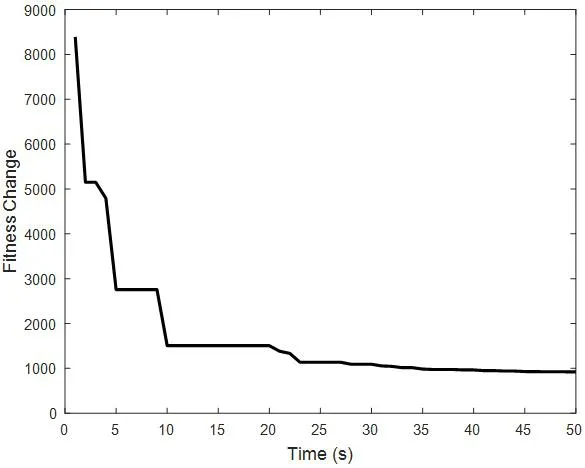
圖5：目標函數的優化過程

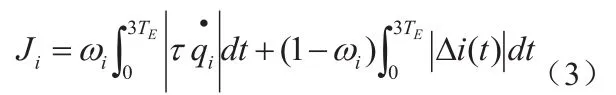
其中ωi為權值，τ為控制輸入信號，為實際軌跡與理想軌跡的差值。

針對雙關節機械手，總的目標函數為：

在這里控制輸入信號使用PD控制器：

其中e定義跟蹤誤差。

3 MATLAB仿真

雙關節機械手的動力學模型可描述為：

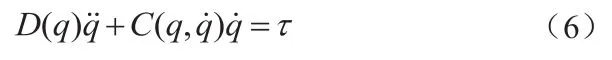
4 結語

經過算法優化可見，運行軌跡平穩，目標函數優化速度較快，機械手運行穩定，無抖動。在初始運動時由于重力作用，力學變化較為劇烈，所需調節輸入調整較多，這一部分可以通過調高采樣頻率使其更加平穩。