追根溯源 “圓”來如此

文武益燕

（作者單位：江蘇省無錫市蠡園中學）

圓作為初中數學里一個重要的幾何圖形，其知識點眾多。圓中的弧、弦、圓心角、圓周角、切線等有很多常用的性質，在處理圓的相關問題時常常要結合數學中的其他知識綜合解決。因此，同學們在解題時需結合圖形，認真分析隱含條件，追根溯源，結合已有的學習經驗，聯想相關知識，作出輔助線，發現此類問題“圓”來如此。

一、圓中重要的角——圓周角與圓心角

例1 如圖1，△ABC內接于⊙O，若∠A=α，則∠OBC等于（ ）。

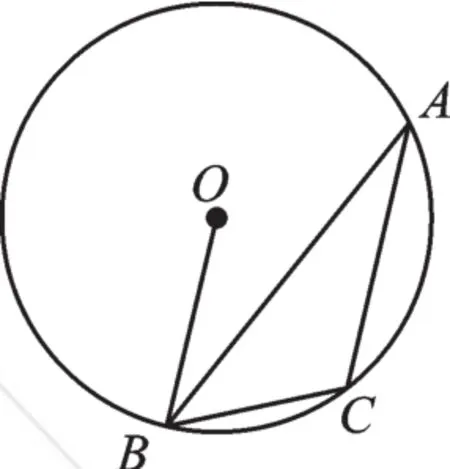
圖1

A.180°-2α B.2α

C.90°+α D.90°-α

【分析】本題要求∠OBC，觀察發現它既不是圓周角也不是圓心角。首先想到將其放到一個三角形中，于是連接半徑OC，這樣∠OBC就是等腰△OBC中的一個底角，只需求出頂角∠BOC即可；而頂角是一個圓心角，于是想到同弧所對的圓周角∠A，這樣∠OBC的度數即可求出。

解：如圖2，連接OC，

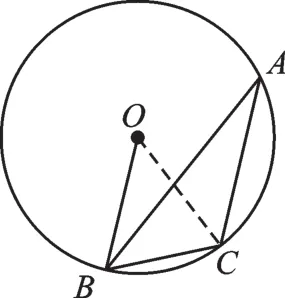
圖2

∵△ABC內接于⊙O，∠A=α，

∴∠BOC=2∠A=2α，

∵OB=OC，

∴∠OBC=∠OCB=90°-α。

故選：D。

【點評】本題考查了圓周角的性質，“同弧所對的圓周角是圓心角的一半”。其實在圓中，圓周角和圓心角猶如一對“雙胞胎”，形影不離。在做題時我們要能夠靈活地進行相互轉化。當然，圓中的輔助線——“連半徑”也是常作的輔助線，這里就構造出了等腰三角形。

例2 如圖3，△ABC內接于半徑為5的⊙O，圓心O到弦BC的距離等于3，則∠A的正切值等于（ ）。

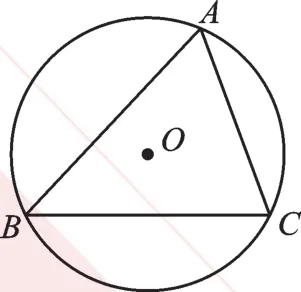
圖3

【分析】求∠A的正切值，可是∠A并不在一個直角三角形中，它是一個圓周角，于是想到同弧BC所對的圓心角。連接半徑OB、OC，再利用垂徑定理，可以進行相等角的轉化，最后解直角三角形即可。

解：如圖4，過點O作OD⊥BC，垂足為D，連接OB、OC。

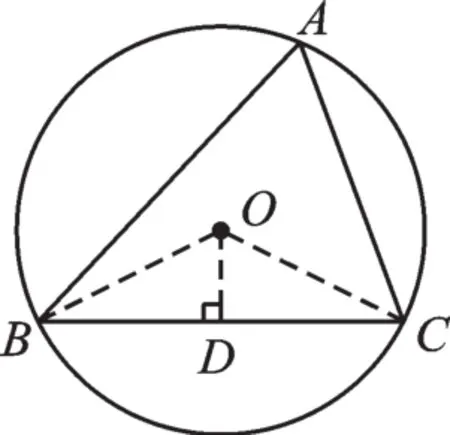
圖4

故選：D。

【點評】在非直角三角形中求一個角的三角函數值，我們的常用方法是構造直角三角形或是通過相等角的轉化思想來解決問題。

二、圓中重要的定理——垂徑定理

例3 如圖5，AB是⊙O的直徑，且經過弦CD的中點H，已知BD=5，則OH的長度為 _____。

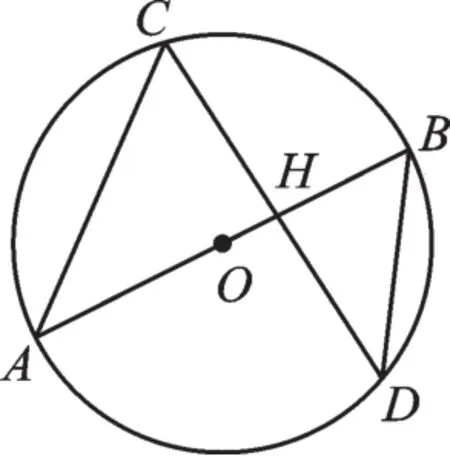
圖5

【分析】由條件“直徑經過弦CD的中點H”，根據垂徑定理得出AB⊥CD，連接OD。在Rt△BDH中，由三角函數求出DH=4，由勾股定理得出BH=3，設OH=x，則OD=OB=x+3，在Rt△ODH中，由勾股定理得出方程，解方程即可。

解：如圖6，連接OD。

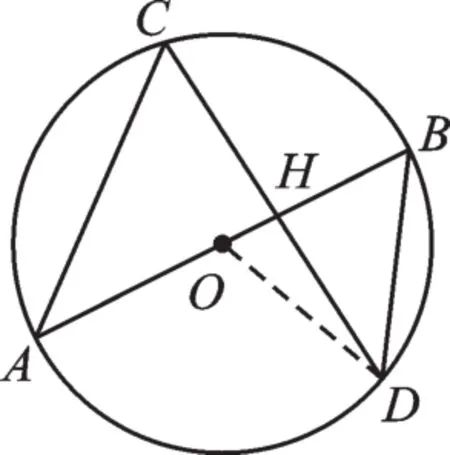
圖6

∵AB是⊙O的直徑，且經過弦CD的中點H，

∴AB⊥CD，

∴∠OHD=∠BHD=90°。

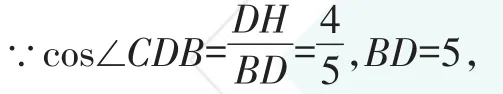
∴DH=4，

∴BH=3，

設OH=x，則OD=OB=x+3，

在Rt△ODH中，由勾股定理得：

x2+42=（x+3）2，

【點評】垂徑定理是一個非常重要的定理，它揭示的是圖形的位置關系和數量關系。在圓中，常常會添加與垂徑定理相關的輔助線，比如連接半徑、過圓心作弦的垂線段等，目的都是為了構造直角三角形這個基本圖形，而勾股定理的運用在問題的解決中往往發揮著不可替代的作用。

例4 如圖7，Rt△ABC內接于⊙O，BC為直徑，AB=4，AC=3，D是弧AB的中點，CD與AB的交點為E，則等于_______。

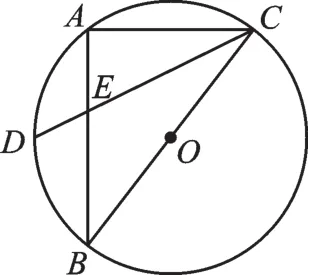
圖7

【分析】由D是弧AB的中點，聯想到連接OD，交AB于點F，利用垂徑定理的推論得出DO⊥AB，AF=BF，發現FO是△ABC的中位線，進而得出DF的長和△DEF∽△CEA，再利用相似三角形的性質求出即可。

解：如圖8，連接DO，交AB于點F。

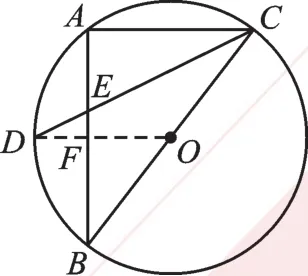
圖8

∵D是弧AB的中點，

∴DO⊥AB，AF=BF，

∴FO是△ABC的中位線，AC∥DO。

∵BC為直徑，AB=4，AC=3，

∴DO=2.5，

∴DF=2.5-1.5=1。

∵AC∥DO，

∴△DEF∽△CEA，

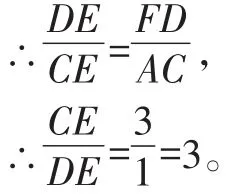
【點評】圓中出現弧的中點以及弦，該中點和圓心連接的這條半徑肯定要作出來，因為正好可以利用垂徑定理，得出平分弦、垂直于弦的結論。線段的比例問題，常常需聯想相似。本題根據已知得出△DEF∽△CEA是解題關鍵。

三、圓中重要的位置關系——點與圓、直線與圓

例5 如圖9，在矩形ABCD中，AB=4，AD=3，以頂點D為圓心作半徑為r的圓，若要求另外三個頂點A、B、C中至少有一個點在圓內，且至少有一個點在圓外，則r的取值范圍是_______。

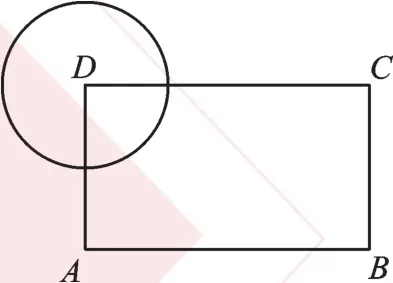
圖9

【分析】要確定點與圓的位置關系，主要根據點與圓心的距離d與半徑r的大小關系來進行判斷。當d＞r時，點在圓外；當d=r時，點在圓上；當d＜r時，點在圓內。

解：連接BD，在Rt△ABD中，AB=4，AD=3，則BD=

由圖可知3＜r＜5。故答案為：3＜r＜5。

【點評】本題主要考查了點與圓的位置關系，其評判標準主要是看d與r的大小關系。

例6 以坐標原點O為圓心，作半徑為2的圓，若直線y=-x+b與⊙O相交，則b的取值范圍是_______。

【分析】本題是幾何問題，但題目沒有給出圖形，所以我們第一步應先畫出半徑為2的圓。直線y=-x+b這個解析式中k=-1，已經暗示了直線的特征，單調遞減，傾斜角是135°。直線與圓相交的情況太多了，所以應聯想到臨界狀態，直線與圓相切時的情形。求出直線y=-x+b與圓相切的兩個b值，則相交時b的值在相切時的兩個b值之間。

解：當直線y=-x+b與圓在第一象限相切，且直線經過一、二、四象限時，如圖10。

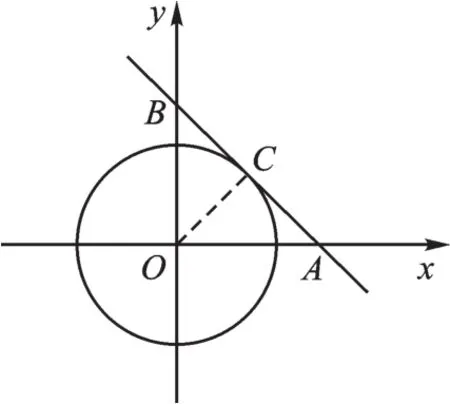
圖10

在y=-x+b中，令x=0時，y=b，則與y軸的交點是（0，b），

當y=0時，x=b，則直線與x軸的交點是（b，0），則OA=OB，即△OAB是等腰直角三角形。

連接圓心O和切點C，則OC=2，

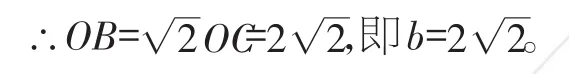
同理，當直線y=-x+b與圓在第三象限相切，且直線經過二、三、四象限

【點評】本題考查了直線與圓的位置關系，其中直線與圓相切是最特殊的位置關系，是中考考查的重點。遇36 難點突破切線，我們有句口訣，“見切點，連半徑，得垂直”，然后解直角三角形即可。當然我們也要注意，當題目中沒有給出圖形時，自己畫圖過程中要考慮是否有多種情形，不要漏解。