基于改進經(jīng)驗小波變換的滾動軸承故障特征提取方法研究

劉自然 胡毅偉 石璞 李謙 尚坤

摘要：針對振動信號的非線性、非平穩(wěn)性和早期故障特征信號難以提取的特點，提出一種基于改進經(jīng)驗小波變換的故障特征提取方法。通過包絡(luò)分析和對包絡(luò)曲線進行閾值分割修整的方法來確定經(jīng)驗小波變換分解的模態(tài)數(shù)和頻率邊界，解決傳統(tǒng)經(jīng)驗小波變換需要預(yù)先設(shè)置分解模態(tài)數(shù)和難以對信號頻譜進行適當(dāng)分割問題，以實現(xiàn)對振動信號故障信息更準(zhǔn)確的描述。實驗表明，該頻譜分割方法能夠有效檢測信號最佳模態(tài)分解數(shù)，使得信號的頻譜分割更為容易、可靠。相比傳統(tǒng)EWT和EMD，改進經(jīng)驗小波變換的滾動軸承內(nèi)圈、外圈Hilbert變換時頻圖對振動信號的故障相關(guān)特征描述更為清晰，在滾動軸承故障特征提取方面表現(xiàn)更為優(yōu)越。

關(guān)鍵詞：滾動軸承;經(jīng)驗小波變換;頻譜劃分;特征提取

中圖分類號：TH113.1 文獻標(biāo)志碼：A 文章編號：1674-5124（2019）10-0010-06

收稿日期：2018-12-07;收到修改稿日期：2019-02-20

基金項目：河南省自然科學(xué)基金（182300410234）

作者簡介：劉自然（1962-），男，河南信陽市人，教授，碩士，研究方向為動態(tài)測試技術(shù)、機電傳動與控制技術(shù)。

0 引言

機械設(shè)備出現(xiàn)故障往往帶來重大經(jīng)濟損失，而其振動信號中含有非常重要的特征信息，通過采集振動信號進行分析處理是一種常用的監(jiān)測方法。旋轉(zhuǎn)機械出現(xiàn)故障時，振動信號呈現(xiàn)非線性、非平穩(wěn)性特點，實現(xiàn)該特點下表征故障的敏感特征提取是進行高精度故障診斷的重要前提[1-2]。

EMD是一種自適應(yīng)時頻分析法，能夠自適應(yīng)的提取振動信號不同時間尺度的本征模態(tài)函數(shù)（intrinsic mode functions，IMF），并通過Hilbert變換求出包絡(luò)幅值和瞬時頻率來表征信號的時頻分布[3]。李鋒等[4]將EMD與AR模型系數(shù)結(jié)合驗證了該特征提取方法的有效性。Su Zuqiang等[5]通過對EMD分解后的IMFS進行時域、頻域等進行特征提取采用LSSVM分類，證明了該方法的有效性。但是EMD存在模態(tài)混疊、端點效應(yīng)以及計算效率低等缺點。為此，Gilles[6]提出一種信號分解方法，即經(jīng)驗小波變換（empirical wavelet transform，EWT），與EMD相比，由于EWT的計算是非遞歸的，所以它在信號分解方面效率更高。劉自然等[7]通過EWT和包絡(luò)譜結(jié)合驗證其在軸承故障診斷的有效性;李志農(nóng)等[8]將EWT應(yīng)用于機械故障診斷中，結(jié)果表明相比于EMD，EWT消除虛假模態(tài)，大大降低計算量。

然而，EWT也存在一些問題，EWT需要預(yù)先設(shè)置分解的模態(tài)數(shù)和頻率邊界，對這些參數(shù)的設(shè)置不當(dāng)將導(dǎo)致信號特征的不準(zhǔn)確提取，針對此問題，本文提出了一種新的頻譜分割方法對傳統(tǒng)EWT進行改進，并在滾動軸承上驗證了其有效性。

1 經(jīng)驗小波變換簡介

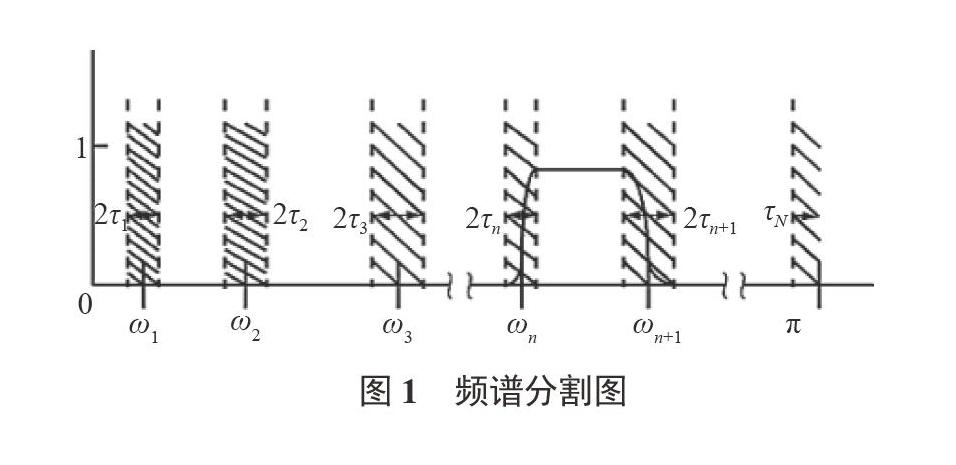
EWT首先用N+1條邊界線將傅里葉頻譜劃分成N個連續(xù)的區(qū)間，除去0和π兩個邊界，還需要N-1個邊界，每個分割的區(qū)間表示為∧_n=[ω_n-1，ω_n]，n=1，2，…，N（ω₀=0，ω_N=π）。其中圍繞每個ω_n都定義一個過渡段T_n（寬度是2τ_n），τ_n=τω_n，γ為系數(shù)[9-10]。具體劃分如圖1所示。

確定分割區(qū)間∧_n后，根據(jù)Meyer小波的構(gòu)造方法構(gòu)建經(jīng)驗小波，經(jīng)驗尺度函數(shù)和經(jīng)驗小波函數(shù)[11]分別為：

|ω|≤ω_n-τ_n

信號重構(gòu)的結(jié)果如下：

通過上式可知經(jīng)驗?zāi)B(tài)函數(shù)f_k，公式如下：

可以看出：EWT具有從非線性、非平穩(wěn)性信號中提取AM-FM分量的優(yōu)點，然而其還具有一定的局限性如下：

1）EWT需要預(yù)先設(shè)置分解的模態(tài)數(shù)，而設(shè)置了不恰當(dāng)?shù)姆纸饽B(tài)數(shù)將會影響特征提取效果。

2）上文中通過τ_n=γω_n構(gòu)造的不同中心頻率的濾波器是一種平均劃分的帶寬定義方法，對于變工況下特征頻率變化的振動信號不能自動定義帶寬區(qū)間。

2 改進經(jīng)驗小波變換

本文提出的頻譜分割方法先對信號的頻譜進行包絡(luò)分析，再通過閾值分割對所得包絡(luò)曲線進行修整。在修整后包絡(luò)曲線中，能夠明顯識別出信號的主頻率分量，主頻率分量將用于確定EWT的模態(tài)數(shù)和頻率邊界。假設(shè)振動信號x（t），改進EWT頻譜分割方法步驟如下：

1）對x（t）進行FFT，即：

F（s）=FFT（x）（8）

A_ax=|F（s_i）|（i=1，2…，l）（9）其中，l為信號x（t）內(nèi)所包含的一半的數(shù)據(jù)。

2）查找A_ax的局部極值。

3）用三次樣條插值法生成傅里葉譜包絡(luò)曲線。

4）計算閾值T：

T=Al+r（A_h-A_l）（10）

r=C/SNR（11）其中，A_h、A_l分別為頻譜中的最大值和最小值。r與信噪比（SNR）成反比。常數(shù)C控制閾值的大小。本文假設(shè)振動信號的信噪比大于85dB，C=10，則r取0.1。

5）使用計算的閾值修整包絡(luò)曲線，并檢測修剪后的包絡(luò)曲線中的所有極值。

6）定位所有局部極大值點。局部極大值點的個數(shù)即為EWT分解的模態(tài)數(shù)，其頻率用于定義模態(tài)的中心頻率。

7）定位所有局部極小值點并按升序排序，即ω=ω₁，…，ω_n-1，ω_n，…，ω_N，用來進行頻譜分割。

通過上述頻譜分割改進方法可得知，第五步的修整過程能夠確定不同振動信號所分解的模態(tài)數(shù)量;并且在包絡(luò)曲線中采用局部附加的方法定義模態(tài)邊界，可使頻譜分割過程更為簡便。

3 改進經(jīng)驗小波變換分析

通過一組正常狀態(tài)軸承信號驗證所提頻譜分割方法的有效性，其時域圖見圖20對信號進行FFT，得到的頻譜圖和包絡(luò)曲線如圖3所示。

利用式（10）進行閾值計算，得T=2。再通過閾值對包絡(luò)曲線進行修剪，得包絡(luò)曲線如圖4所示。

通過所提方法的6）和7），利用修剪得到的包絡(luò)曲線來分割頻譜。圖4中模態(tài)的頻率邊界由虛線表示。不難看出，該信號的頻譜共被分割成11個部分，由6個主模態(tài)邊界組成。

為檢驗所提頻譜分割方法的效果，對原始信號和EWT分解重構(gòu)的信號進行相關(guān)分析。假設(shè)EWT分解的模態(tài)數(shù)越多，其重構(gòu)信號與原始信號的相關(guān)性越大。為得到兩者相關(guān)性的變化趨勢，本文預(yù)先設(shè)置EWT分解模態(tài)數(shù)為11，并利用EWT對圖2信號進行分解再重構(gòu)，重構(gòu)信號與原始信號相關(guān)系數(shù)的公式如下：其中，x為原始信號，表示重構(gòu)信號，其中n從1增加到11，表示用于信號重構(gòu)的模態(tài)數(shù)。

相關(guān)系數(shù)值C（n）與信號重構(gòu)模態(tài)數(shù)的變化趨勢如圖5所示。

從圖中可知，隨著n的增加，C（n）也逐漸變大，當(dāng)n為11時，C（n）趨近于1。同時可觀察到當(dāng)n=1，2，4，6，8和10時，C（n）出現(xiàn)明顯的增長。代表這6種模態(tài)為信號主要特征，即這6種模態(tài)重構(gòu)的信號能夠有效刻畫原始信號的主要特征。此結(jié)果與所提分割方法的結(jié)果相一致。表明本文所提頻譜分割方法能夠有效檢測信號最佳模態(tài)分解數(shù)。

本文所提改進EWT流程圖如圖6所示。

4 改進經(jīng)驗小波變換實驗驗證

本實驗利用已開放供研究的凱斯西儲大學(xué)軸承數(shù)據(jù)中心軸承故障數(shù)據(jù)進行驗證。通過電火花加工（EDM）對電機軸承內(nèi)圈和外圈設(shè)置直徑約0.2mm的故障損傷。實驗臺由電機速度控制器，2馬力電機，模擬載荷等組成。當(dāng)電機轉(zhuǎn)速為1750r/min時通過加速度傳感器采集內(nèi)圈故障和外圈故障的振動信號，采樣頻率為12kHz。兩種信號的時域波形圖如圖7所示。

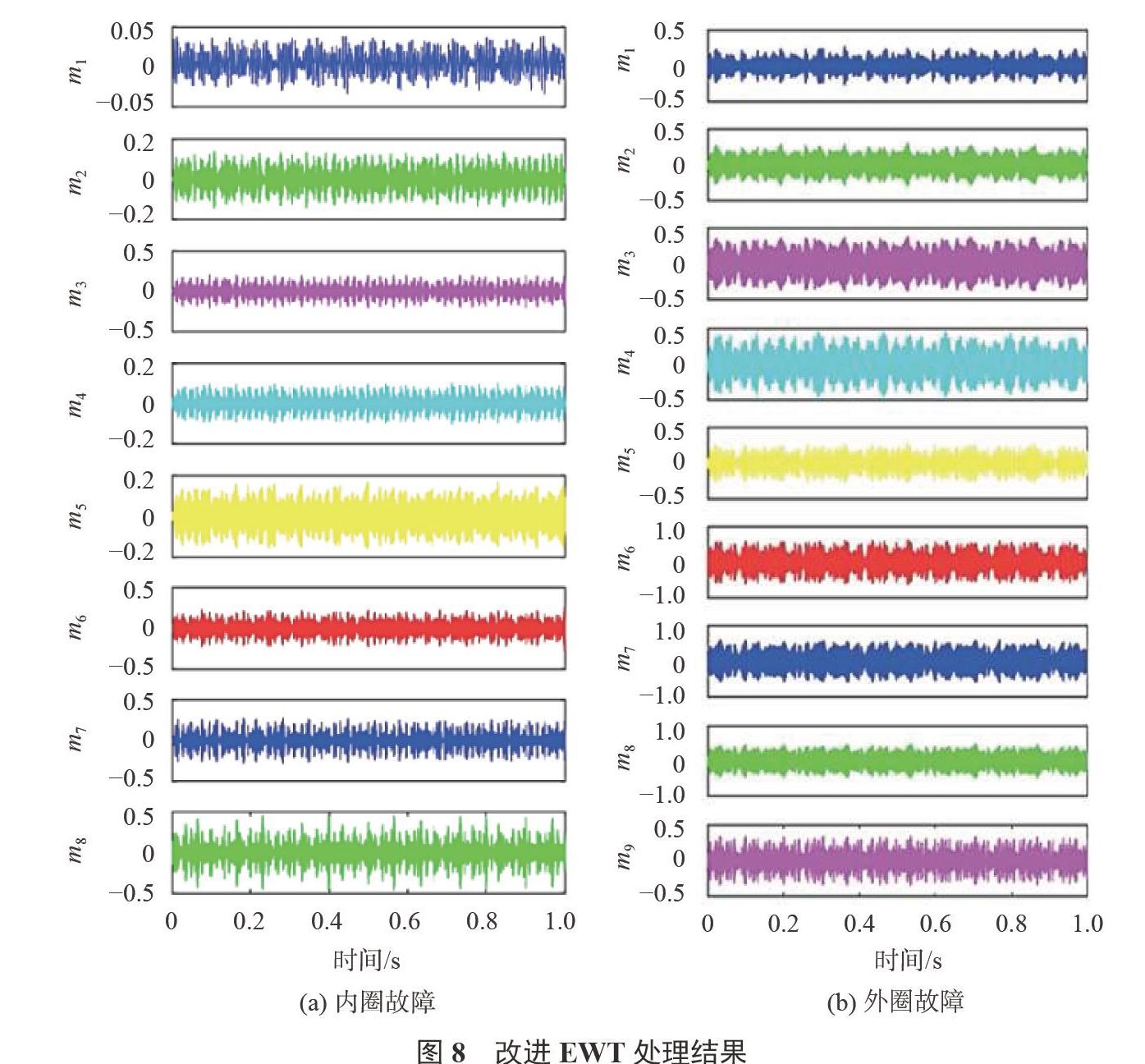
從圖中可以看出，兩種振動信號都存在很強的背景噪聲，可以明顯看出振動信號中包含復(fù)雜的沖擊特征。通過改進EWT對兩種振動信號處理得到的主要模態(tài)如圖8所示。

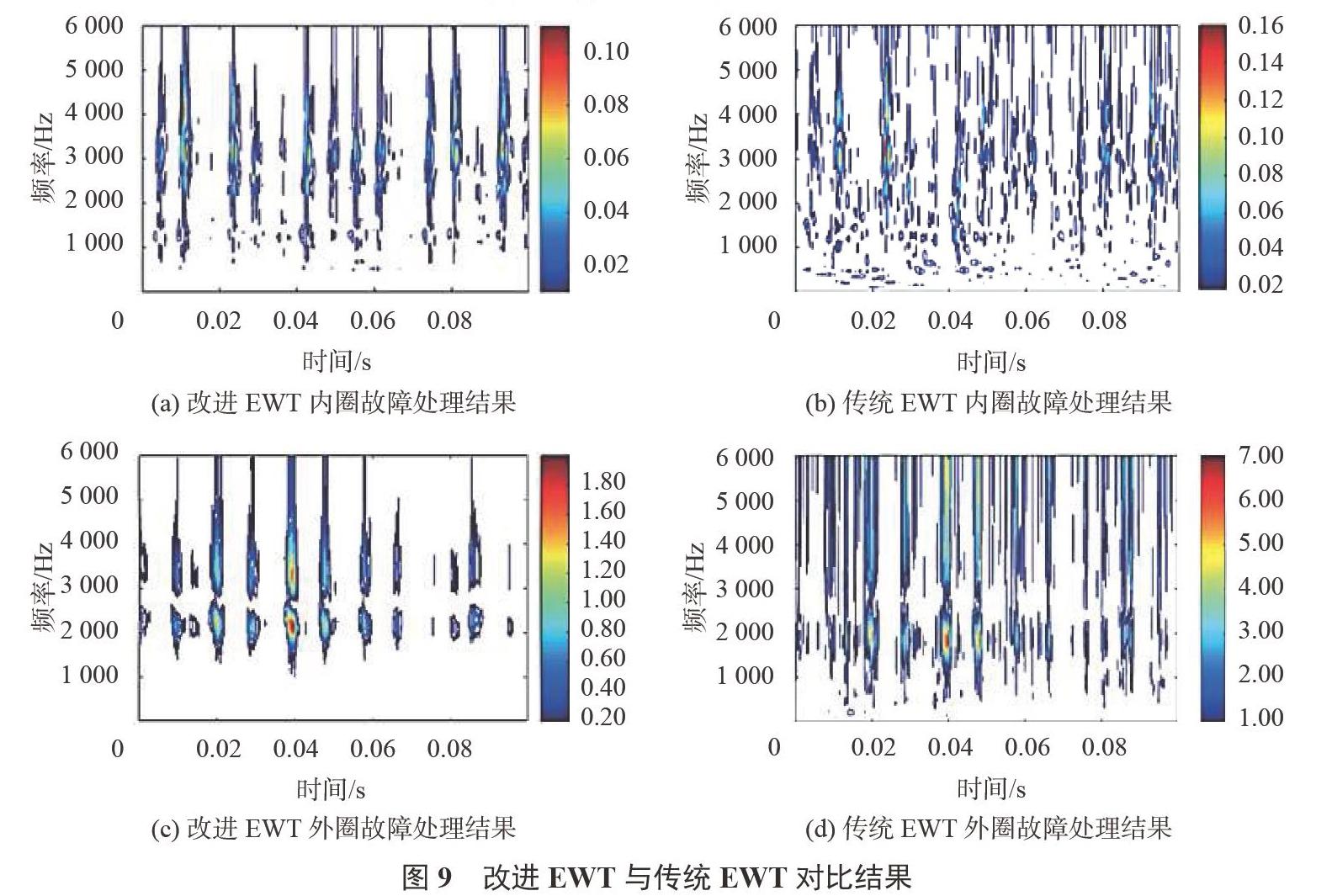
為了準(zhǔn)確描述故障相關(guān)的特征，通過對圖8所示的各個模態(tài)函數(shù)進行Hilbert變換，圖9為相應(yīng)的兩種故障信號的時頻圖。受計算機內(nèi)存的限制，在時頻分析中只處理圖8（a）、8（b）中的前0.1s數(shù)據(jù)。同時為了對比改進EWT效果，圖9展示了使用傳統(tǒng)的EWT得到的時頻圖。

對圖9所示結(jié)果進行比較可知：

信號中包含的與故障相關(guān)的周期性沖擊特征已被改進EWT顯式地檢測出來。從這些周期性沖擊特征之間的時間間隔可以很容易地估計出故障的特征頻率，因此，在已知軸承的規(guī)格參數(shù)情況下，能夠準(zhǔn)確地診斷故障類型。相反，傳統(tǒng)小波變換導(dǎo)出的時頻圖中沖擊特征表現(xiàn)不明顯，甚至被背景噪聲掩蓋，導(dǎo)致它們之間的時間間隔很難估計，這將增加信號解析的難度。

傳統(tǒng)EWT結(jié)果中存在大量改進EWT結(jié)果所不存在的干擾分量。說明改進EWT能夠?qū)⒄駝有盘柕闹黝l率分量準(zhǔn)確提取出來的同時對信號中存在的干擾和噪聲的抑制效果更好，從而使信號的時頻圖更加整潔、易于觀察。

在此基礎(chǔ)上，對改進EWT和DM進行對比，以說明改進EWT對非線性和非平穩(wěn)振動信號特征提取的優(yōu)越性。圖7中兩個信號的對應(yīng)OM結(jié)果如圖10所示。

從圖10中可以看出，在早期故障階段信號中的沖擊特征很弱的情況下，能夠被改進EWT準(zhǔn)確提取出的故障沖擊特征通過EMD方法不能實現(xiàn)成功提取。

實驗表明，與EMD和傳統(tǒng)EWT相比，改進EWT在準(zhǔn)確提取非線性非平穩(wěn)性狀態(tài)監(jiān)測信號的時頻特征方面的效果更好。因此通過改進EWT得到的精確、整潔的時頻特征對于滾動軸承故障診斷具有更大的幫助。

5 結(jié)束語

EWT在信號分解和特征提取方面均優(yōu)于EM1）。然而，EWT結(jié)果的準(zhǔn)確性在很大程度上取決于模態(tài)數(shù)的正確設(shè)置和每個模態(tài)的頻率邊界劃分。為解決此問題，本文提出了一種改進的EWT方法，并進行了實驗驗證，得到結(jié)論如下：

1）傳統(tǒng)的EWT方法由于缺乏對所研究信號的頻譜進行適當(dāng)分割的方法，因此無法對信號的頻譜進行適當(dāng)分割。而信號頻潛分割不當(dāng)將會降低EWT的計算效率以及降低特征提取的準(zhǔn)確性。

2）利用所提出的頻譜分割方法，可以很容易地確定每個EWT模態(tài)的模態(tài)數(shù)目和頻率邊界。此外，通過改進EWT得到的每個EWT模態(tài)都具有滾動軸承特征相對應(yīng)的確切物理意義。而傳統(tǒng)EWT將未識別的信息包含在結(jié)果中，將會增加信號解析的難度，甚至誤導(dǎo)滾動軸承的狀態(tài)監(jiān)測。

3）實驗表明，盡管信號中含有相當(dāng)大的噪聲，改進EWT仍能更精確地提取與故障相關(guān)的信號時頻特征。與傳統(tǒng)EWT相比，改進EWT需要較少的人為參與，因此有可能成為一種完全由數(shù)據(jù)驅(qū)動的信號處理技術(shù)。

參考文獻

[1]吳印華，徐瓊燕，李俊峰.基于局部特征尺度分解排列熵和線性局部且空間排列的故障特征提取方法[J].機械設(shè)計與研究，2017，33（1）：27-30，34.

[2]張良，張前圖.基于LCD模糊熵和流行學(xué)習(xí)的故障特征提取方法[J].機械強度，2016，38（2）：225-230.

[3]宋金波，王德平，劉霞.基于EMD瞬時功率譜熵的神經(jīng)網(wǎng)絡(luò)滾動軸承故障診斷[J].化工自動化及表，2016，43（8）：793-796.

[4]李鋒，湯寶平，陳法法.基于線性局部切空間排列維數(shù)化簡的故障診斷[J].振動與沖擊，2012，31（13）：36-40，61·

[5]SU Z Q，TANG B P，LIU Z R，et al.Multi-fault diagnosis forrotating machinery based on orthogonal supervised linear localtangent space alignment and least square supportvectormachine[J].Neuro-Computing，2015，157（1）：208-222.

[6]GILLES J.Empirical wavelet transform D].日;EE Transactionson Signals Processing，2013，61（16）：3999-4010.

[7]劉自然，陳仁權(quán)，顏丙生，等.基于EWT和包絡(luò)譜分析的軸承故障診斷研究[J].中國測試，2018，44（2）：98-102.

[8]李志農(nóng)，朱明，褚福磊，等.基于經(jīng)驗小波變換的機械故障診斷方法研究[J].儀器儀表學(xué)報，2014，35（11）：2423-2432.

[9]向玲，李媛媛.經(jīng)驗小波變換在旋轉(zhuǎn)機械故障診斷中的應(yīng)用[J].動力工程學(xué)報，2015，35（12）：975-981.

[10]祝文穎，馮志鵬.基于改進經(jīng)驗小波變換的行星齒輪箱故障診斷[J].儀器儀表學(xué)報，2016，37（10）：2193-2201.

[11]FRANCIS A，MURUGANANTHAM C.An adaptive denoisingmethod using empirical wavelet transform[J].InternationalJournal of Computer Applications，2015，117（21）：18-20.

（編輯：劉楊）