U型截面薄壁件測量精度優化方法研究

摘要：為提高三坐標測量機在測量一種U型截面薄壁件時的測量精度，分別從溫度和測量力兩方面研究精度優化方法。基于物體熱膨脹效應的原子熱振動原理分析鋁合金材料的熱膨脹影響因素，將溫度影響引入測量能力評估算法，得到可實施溫度補償的邊界條件，利用Minitab對變溫測量實驗數據進行分析并擬合出該薄壁件在徑向方向上的熱膨脹函數，實現在溫度邊界范圍內對測量結果進行精度優化;針對RDS XXT測頭系統的內部構造，通過對測頭結構進行力學分析并建立采點觸發力學模型，確定該測頭系統的采點觸發模式為力矩觸發，利用材料力學理論分析力矩觸發模式下的被測件形變機理。測力及測量截面位置交叉測量實驗結果表明：測桿長度越長，測力越小，且越靠近工件底部，測量誤差越小，測量精度越高。

關鍵詞：三坐標測量機;薄壁件;溫度補償;測量變形;測量精度

中圖分類號：TB921 文獻標志碼：A 文章編號：1674-5124（2019）09-0021-06

收稿日期：2019-03-11;收到修改稿日期：2019-05-08

作者簡介：王斌（1982-），男，天津市人，高級工程師，碩士，研究方向為精密測試技術。

0 引言

工業坐標測量機是國內外幾何量測量領域普遍使用的精密測量設備，其測量精度的影響因素很多，包括靜態因素和動態因素兩大類[1-2]。靜態因素主要包括溫度、振動、量值溯源等;動態因素主要包括測量策略、測量力等。通過研究和分析國內外計量測試行業最新技術發展動態發現，為了有效減小測量誤差，普遍采取制定國家或行業標準對坐標測量進行規范，如德國的VDA標準，嚴格規范了坐標機在使用環境、量值溯源等方面的技術要求，并強制貫標執行，使靜態誤差因素得到有效控制;歐洲的AUKOM坐標測量行業認證機構則通過實行技術資格認證制度，特別是對于形位公差的測量，建立了AUKOM GD&T專項認證標準，進而對坐標機的測量策略進行統一和規范，有效減少了動態因素所導致的誤差[3-4]。

通過上述分析可以看出，三坐標測量機的測量多數誤差來源可通過制定行業標準或加強操作的一致性加以消除，但是對于工件自身溫度差異以及結構特點在測量時產生的測量誤差，就需要結合材料的熱膨脹系數和測力作用機理加以分析并優化，從而提高測量精度。國內外學者在這一領域進行了廣泛研究。Valkov等[5]研究了航空鋁合金板材的熱膨脹系數，認為材料厚度對熱膨脹變形有重要影響，并介紹了適于做熱膨脹系數測定的制樣方法，并采用光學法測量熱膨脹系數。Kompan筀[6]分析了鋁合金產品的不同設計結構與熱膨脹系數的關系。上述研究主要解決鋁合金材料熱膨脹系數的測定精度、測定條件等問題[7]，缺乏對采用坐標測量機測量鋁合金產品時工件溫度與測量精度的關系分析，特別是對于薄壁件，其溫度對測量精度的影響和補償方法，尚未做相關深入研究。Laaouina等[8]研究了接觸式測頭采點觸發時測力在工件表面的作用機理，以及工件由測力所導致的形變規律。Pan等[9]通過分析坐標機廣泛采用的壓電式觸發測頭的采點觸發模式，建立力學模型，通過計算得到了測力對測量精度的影響關系式。上述研究雖然是針對壓電式坐標機測頭進行的分析研究，但對于本文研究具有重要的參考和借鑒意義[10]。

本文將對一種中心對稱剖面呈U型的鋁合金薄壁回轉零件進行測量精度的溫度補償方法和測力影響消除方法研究。通過建立一種帶入溫度影響因素的測量能力評估算法，確定溫度誤差補償的邊界條件并擬合補償算式;提出一種針對環形觸發測頭系統測力分析的力學模型，研究測力導致的形變機理，減小測力影響，提高測量精度。

1 工件溫度對測量精度的影響分析及補償方法

1.1 金屬熱膨脹模型分析及精度優化方法

熱膨脹特性是物體的基本屬性，由原子的熱振動效應產生。根據原子理論模型可知，原子間勢能u（r）與原子間的相互距離r存在一定的函數關系，因此，當原子間發生相互振動時，其間距由r₀變為r₀+x，而勢能變為：

u（r）=u（r₀+x）（1）

由熱力學統計原理及熱膨脹系數概念，可得到物體的熱膨脹系數α_CTE，T：

上式表征的是不同材料的熱膨脹系數隨著溫度的不同而發生變化，由于鋁合金的熱膨脹系數受組分比例、金相組織、相間缺陷、相間差異性及加工工藝的熱效應等因素影響[11]，其熱效應很難用經典熱膨脹系數計算方法得到。那么，在實際測量時，為研究鋁合金的熱膨脹特性，通常采用鋁合金試件溫度變化引起特定尺寸方向伸長量進行測試，繪制關系曲線，進而對不同溫度時材料的熱膨脹效應進行分析。

1.2 精度優化邊界的溫度條件

根據測量能力評估方法，測量設備的測量誤差至少要小于被測參數設計公差的1/4，而被測工件的熱形變所導致的偏差應與設備自身測量誤差合并考慮，累計誤差與被測參數設計因滿足如下關系[12]：

（δ_熱形變+δ_測量誤差）熱形變

1.3 溫度補償算式擬合

選取100件U型截面薄壁件，分別在17～23℃的溫度范圍內，測量各試件的直徑、圓度、高度等設計參數，同時，測量過程中保持測量環境溫度恒定。測量實驗結果表明，溫度影響主要體現在徑向尺寸上。為此，以100個試件在不同溫度條件下的測量平均值作為擬合元素，利用Minitab數據分析軟件進行分析，生成溫度系數函數模型如下：

φD=0.005229×T+C（7）其中，C為U型薄壁件的名義直徑。溫度系數函數模型可通過計算得到不同溫度條件下的補償值，可用于測量室在不具備恒溫條件下的實時測量結果修正，保證了測量結果的準確性。

1.4 溫度補償結果驗證實驗

通過選取5個實驗件，將其分別恒溫至17～23℃范圍內的各溫度點，測量各溫度點下的測量值并作為比對數據，利用比對數據與標準溫度下（20℃）時的測量值（參考數據）進行對比，驗證補償效果，考核測量精度。實驗結果如表1所示。

由表可知，5個測試件中補償前測量誤差最大達到0.021mm，而補償后最大誤差僅為0.005mm，測量精度有了提高了4倍多。通過溫度補償，在工件未完全恒溫的狀態下，有效提高了坐標機的測量精度。

2 測力對精度的影響機理及優化方法

2.1 測頭觸發模式與測力的關系

三坐標測量機用測頭可分為動態測頭與靜態測頭兩大類。Zeiss G2坐標機的RDS XXT測頭系統是可實現動態（掃描式）和靜態（觸發式）測量的雙模式信號采集系統，采用觸發采點測量時，可以看作為靜態測量，此時，測量力對工件造成的影響與測頭系統的結構及觸發模式有關。RDS XXT測頭內部結構如圖1（a）所示，1為測桿，2為環形保持架。測桿安裝在環形保持架上，環形保持架的外壁布有均勻的觸點，當測桿沒有受到測量力時，環形保持架的外壁與觸點均保持接觸;當測桿的球狀端部與工件接觸時，至少會引起一個觸點脫離接觸，從而引起電路的斷開，產生階躍信號，完成測量觸發采點[13]。

接觸測量時，由于測頭和工件存在相對運動，當被測表面有幾何形狀誤差或對基準要素有位置誤差，有可能使測頭瞬時離開被測工件表面而產生測量誤差。為了分析方便，將測針和測桿簡化為等截面的測桿單元，質量為M，長度為L，作用于工件上的靜測量力為F₀。當測針相對工件表面測量時，測桿單元繞支點做左右擺動，擺角為B，則測桿單元的力學方程為

由式（8）可以看出，測頭系統的觸發力學方程與測桿擺角關系較大，測頭系統的結構決定了其擺動距離不大于圖1中觸點球徑，而當θ較小時，該力學模型可簡化為力矩方程，即測量力與測桿長度成反比。說明RDS XXT測頭系統是由力矩觸發采點的，可通過改變測桿長度控制測量力的大小。

如圖1（b）所示，測頭位于坐標系的Z軸的原點，測桿長度為尸，環形保持架半徑OC的投影與X軸夾角φ₀，測頭觸碰零件產生的觸發力為F（θ，φ），擺角θ和方位角φ直接影響觸發力的方向。那么，如果當測頭采點方向與零件柱面法線方向相同，極角θ和方位角φ不超過觸點半徑，則測力F可使測桿圍繞A-B軸旋轉，當環形保持架C離開觸點時信號觸發。因此，為保證采點觸發而加載的測力將會使工件產生接觸形變。此外，該測量力還會對測針造成彎曲，產生彎曲位移，進而導致工件彎曲變形。

2.2 測力所致形變對測量精度的影響

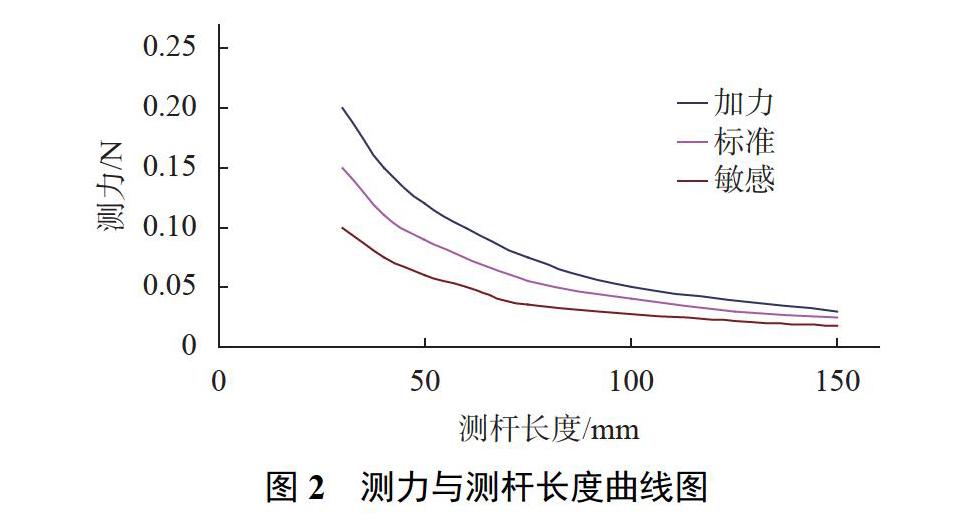
假設零件和測頭不變，那么形變量只與測量力有關[14]，RDS XXT測頭系統配置有3種不同的采點觸發測量力模式，分別為敏感性觸發、標準型觸發和加力觸發，分別對應不同的表面粗糙度狀況的工件，敏感性觸發模式主要用于測量表面光潔度較高的塑料、玻璃等工件的測量;標準型用于大多數金屬材料的機加產品;加力觸發用于表面粗糙的復合材料檢測。因此，對于鋁合金薄壁工件的檢測，應采用標準型觸發模式，其測力與測桿長度關系曲線如圖2所示。

由圖可以看出，隨著測桿長度增加，3種測力模式的測力均呈減小趨勢，當測桿長度為30mm時，3種測力模式的測力差值為0.05N，而當測桿長度為150mm時，測力差值為小于0.01N。

2.2.1 接觸形變量計算

使用接觸式量儀進行測量時，測頭和被測工件的測量面直接接觸，為了保證儀器與工件表面的可靠接觸，需要一定大小的力作用于工件上，但測量力的存在也會使工件和測頭產生接觸變形。接觸變形量的大小與工件的材料、測量力的大小有關[15]。

式中：F——測量力，N;

E——工件的彈性模量，GPa;

R₁——工件半徑，mm;

R₂——測頭半徑，mm。

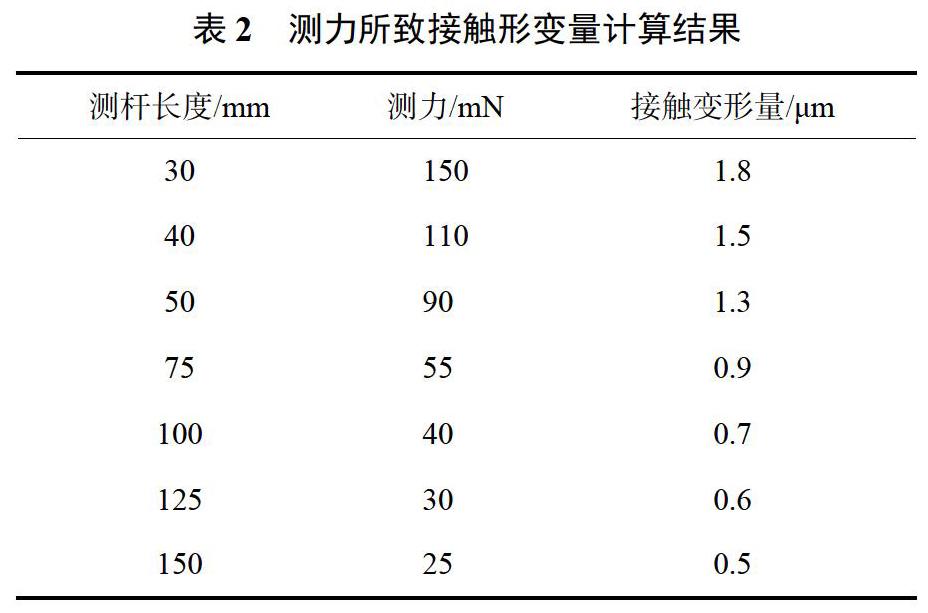
將鋁合金材料彈性模量，測頭球半徑為1.5mm，代入公式（9），得到不同測力條件下的變形量如表2所示。

根據以上分析計算可以看出，當測桿長為30mm時，對應測量力為150mN，工件的接觸變形量為1.8μm，同時由于測量過程中工件接觸的均勻性，考慮到其接觸變形量與被測參數公差比值較小以及測量機自身測量誤差（1.9μm），其變形影響可忽略。

2.2.2 彎曲形變量計算

工件在測量力的作用下也會產生彎曲變形，彎曲變形量主要受測量位置以及測量力大小的影響。根據材料力學理論，工件在測量力的作用下產生的彎曲變形量[16]為

式中：F——測量力，N;

E——工件彈性模量，GPa;

I——工件截面慣性矩，N·m。

工件的彎曲變形不僅和工件的材料有關，其裝夾位置的影響也較大。U型截面薄壁件的剖面尺寸結構如圖3所示。

這樣，可根據下式計算出U型截面薄壁件的慣性矩：

式中：B——工件外徑，mm;

e₁——工件外底面至裝卡截面距離，mm;

b——工件內徑，mm;

h——工件內底面至裝卡截面距離，mm;

a/2——工件壁厚，mm;

e₂——工件端面至裝卡截面距離，mm。

彎曲變形量與裝卡位置的關系，用工件裝夾高度H與工件直徑的比值i作為裝夾位置，考慮到該薄壁件的軸向長度，裝卡位置差△H設置2mm。選取測力為55mN，測桿長度為75mm，將各參數代入公式（10），計算出不同測量截面測量力與彎曲變形量的關系如表3所示。

由表可以看出，隨著測量力的增加，其彎曲變形量也在增加，并且隨著測量位置的升高，其彎曲變形量最大達到了6.2μm，可見彎曲變形的影響是造成測量誤差的主要原因[17]。所以，在測量速度、測量長度一定的條件下，測量采點位置越靠近工件底部，誤差越小，精度越高。

2.3 測力及測量位置與精度關系驗證實驗

2.3.1 測力與精度關系驗證實驗

選取5個U型薄壁件，編號記為1^#～5^#，在同一測量截面高度（△H=2mm）以不同的測量力連續測量10次，記錄并計算10次測量結果的極差值，考核其測量精度，測量實驗結果如表4所示。

由表測量結果可以看出，隨著測量力的不斷增加，測量誤差越來越大，精度逐漸下降。可見，測量力導致的彎曲形變對精度的影響較為顯著，與理論計算結果一致。

2.3.2 測量位置與精度關系驗證實驗

仍選取2.3.1選用的5個試驗件，以相同的測量力（40mN）在不同的截面高度連續測量10次，記錄并計算10次測量結果的極差值，考核其測量精度，測量實驗結果如表5所示。

由表可以看出，隨著測量截面高度的不斷增加，測量誤差越來越大，精度逐漸下降。可見，測量位置距離定位位置越遠，測力導致的彎曲形變效應越顯著，同樣與理論計算結果一致。

3 結束語

本文針對U型截面薄壁件在加工過程中會由熱效應或環境溫度熱傳導而產生變形的特點，通過變溫實驗建立了尺寸溫度補償算式，保證測量結果的準確性;通過分析三坐標測量機RDS XXT測頭系統的結構及采點觸發原理，確定了該測頭系統的靜態測量力所導致工件形變主要為彎曲變形，對于U型截面薄壁易變形件，測量精度實驗結果表明，通過合理配置測桿長度及采點高度，可有效提高此工件的測量精度。

參考文獻

[1]張國雄.三坐標測量機[M].天津：天津大學出版社，1999.

[2]羅哉.關節臂式坐標測量機測量力誤差分析及補償[J].儀器儀表學報，2017（5）：1159-1166.

[3]YOUNES E，ABDERRAZAK E O，AHMED C.Experimentalinvestigation of dynamic errors in coordinate measuringmachines for high speed measurement[J].InternationalJournal of Precision Engineering and Manufacturing，2018，19（8）：1115-1124.

[4]HUSSAIN M，（！U J，ENGEL R，et al.Designed experiment tofind the optimal combination of the factors for the coordinatemeasuring machine（CMM）to measure cylindricity of enginecylinder bore[C]//International Conference on IndustrialEngineering&Operations Management，2015.

[5]VALKOV S，NEOV D，BEZDUSHNYI R，et al.Study of themicrostructure，crystallographic structure and thermal stabilityof Al-Ti-Nb alloys produced by selective electron beamalloying[J].Journal of Surface Investigation：X-ray，Synchrotron and Neutron Techniques，2018，12（3）：436-441.

[6]KOMPAN T A，KONDRATIEV S V，KORENEV A S，et al.Measurement of the thermal expansion coefficient for ultra-high temperatures up to 3000 K[J].International Journal ofThermophysics，2018，39（3）：40.

[7]程湘紅.三坐標測量機測量誤差分析及處理[J].工程技術研究，2018（1）：113-114，160.

[8]LAAOUINA L，NAFI A，MOUCHTACHI A，et al.Application of CMM separation method for identifyingabsolute values of probe errors and machine errors[C]//International Conference on Engineering&Mis，2016.

[9]PAN F，NIE L，BAI Y，et al.Geometric errors measurementfor coordinate measuring machines[J].IOP Conference SeriesEarth and Environmental Science，2017，81（1）：012117.

[10]KALUS J，JORGENSEN J K.Measuring deformation andmechanical properties of weld lines in short fibre reinforcedthermoplastics using digital image correlation[J].PolymerTesting，2014，36：44-53.

[11]丁鴻章.工程金屬材料熱膨脹系數的計算[J].浙江工業大學學報，2000，28（4）：358-366.

[12]黃曉明，孫杰，李劍鋒，等.7050-T7451鋁合金預拉伸板材熱膨脹系數變化規律及機理[J].中國有色金屬學報，2013（12）：3282-3288.

[13]劉育楠，董學軍，劉紅剛，等.三坐標測量機測頭系統精度驗證方法研究[J].工業計量，2016，26（6）：41-45.

[14]邵竑文，孟亮，劉斯宇.論測量力對幾何尺寸測量結果的影響[J].計量與測試技術，2015，42（12）：52-54.

[15]李志渤，黃強先，趙劍，等.接觸測量中的微探球力變形研究[J].中國機械工程，2014（14）：1126-1129.

[16]熊偉，葛志華，唐威，等.輪毅軸承接觸應力及變形量計算與分析[J].機械工程師，2018（10）：119-121.

[17]邱江月，夏金利.探討測量力對測試結果的影響[J].工業計量，2010（2）：365-366.

（編輯：商丹丹）