論克拉維烏斯的二重雙假設法求解公式的一致性

劉 迪，趙繼偉

(西北大學 科學史高等研究院, 陜西 西安 710127)

雙假設法最早記載于中國古典數學名著《算數書》和《九章算術》,后來成為中國古代數學家求解二元線性問題的標準算法。中世紀阿拉伯數學家對該方法做出了重要貢獻,例如,9世紀庫斯塔·伊本·盧卡(Qusta ibn luqa,C.820-912)首次給出雙假設法的幾何證明,阿布·卡米爾(Abu Kamil,C.850-C.930)著有《雙假設法之書》(KitabalKhataayn)[1]。

對于求解多元線性方程組問題,中國古算中使用方程術(亦稱消元法),而歐洲數學家走的是另一條路徑。13世紀初,意大利數學家斐波那契(Fibonacci,C.1170-C.1250)在《計算之書》(LiberAbaci,1202)第13章中,運用多重雙假設法求解了多元線性方程組[2-3],其后三百多年歐洲數學家沿用了他的方法。直至16世紀后期,德國數學家克拉維烏斯(Christopher Clavius,1538—1612)在《算術實踐概要》(EpitomeArithmeticaePracticae,1583)第23章中討論用雙假設法求解三元線性方程組時[4],才首次對斐波那契的方法做出簡化。其中他提出:在運用二重雙假設法求出三元線性方程組的一個未知量之后,可以不必對其他兩個未知量繼續使用雙假設法求解,而是可以通過將第一次求解過程中所產生的相應數據直接代入“求解公式”而得出結果;也就是說,他對3個未知量使用了一致的求解公式。

目前學者對雙假設法的研究主要包括對其起源的探究[5-7],利用相似三角形推導雙假設法求解公式[8-9],分析該方法與單假設法的區別與聯系[10-11]及雙假設法在非線性方程求解中的應用[12-15]等方面。《算法史》(AHistoryofAlgorithms,1999)[1]中對克拉維烏斯使用雙假設法的一個例子給出了英文翻譯(原文為拉丁語),并試圖用現代行列式理論解釋克拉維烏斯二重雙假設法求解公式的一致性,但我們將指出其解釋并不能令人滿意。圍繞克拉維烏斯雙假設法求解公式的一致性,本文將討論以下3個問題:

1)克拉維烏斯如何簡化了雙假設法的計算程序;

2)用空間解析幾何知識解釋雙假設法求解公式一致性的數學原理;

3)提出克拉維烏斯發現求解公式一致性的一種可能思路。

1 克拉維烏斯的雙假設法對斐波那契的簡化

1.1 斐波那契與克拉維烏斯的雙假設法的異同

在《計算之書》第13章中,對于二元線性方程組問題

斐波那契首先將x的假值x1代入其中一個方程,得到問題的假解(x1,y1);然后將其代入另一個方程,得到差值

e1=a2x1+b2y1-d2;

同理可得假解(x2,y2)及其差值

e2=a2x2+b2y2-d2;

接下來就可以利用雙假設法的求解公式

得到x的真值;最后將x0直接代入任一個方程即得y的真值y0。

對三元線性方程組問題,斐波那契針對兩種不同類型的問題給出了不同的解法。第一類問題屬于特殊問題,其題設條件比較簡單,亦即如果求出了一個未知量,那么其他兩個未知量可以直接通過代入法遞次求出。對于這類問題,斐波那契先使用一次雙假設法求出一個未知量的值,比如設為x0;然后根據題設條件的特殊性,將x0的值代入原方程組而直接得到另外兩個未知量的值y0和z0。也就是說,此時他僅使用了一次雙假設法和代入法就解決了三元線性方程組的問題。

第二類三元線性方程組的問題屬于一般問題,其題設條件比較復雜,求出一個未知量的值以后,無法通過代入法而直接得到其他未知量的值。如第三個“三人有第納爾”問題[3],此時相當于求解形如

的三元線性方程組,斐波那契求解x的真值x0的步驟如圖1所示。他首先設出x的假值x1,將其代入比如前兩個方程,得到關于y,z的二元線性方程組

然后利用一次雙假設法求出上述二元方程組的解(y1,z1),即得問題的假解(x1,y1,z1)。同理,他設出x的另一個假值x2,并再次利用雙假設法求解代入x2后所得的方程組

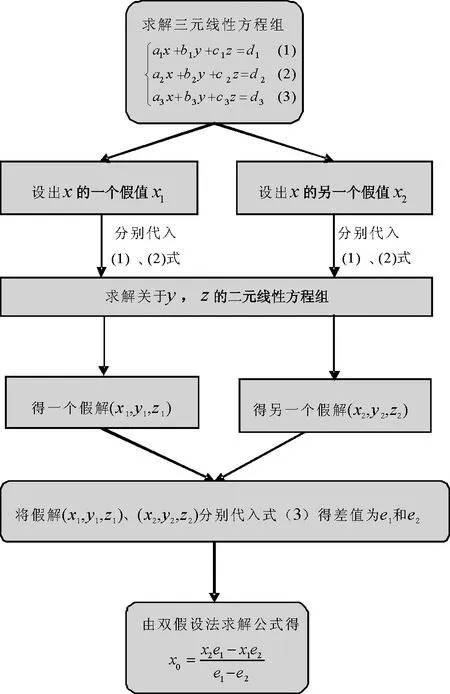
圖1 二重雙假設法相同步驟程序圖Fig.1 Flow diagram of the same procedure of twofold double false positions

得到問題的另一個假解(x2,y2,z2)。至此,他第三次運用雙假設法,將兩個假解(x1,y1,z1)和(x2,y2,z2)分別代入第三個方程,得到對應的差值分別為

e1=a3x1+b3y1+c3z1-d3

和

e2=a3x2+b3y2+c3z2-d3,再由雙假設法求解公式即得x的真值x0。不難看出,斐波那契在求解x的真值的過程中運用了嵌套式的雙假設法,其中前兩次用來求兩個假解的雙假設法作為第一重嵌套在用來求x的真值的第三次雙假設法內,整個求解程序共使用了3次雙假設法,我們把這種做法稱為二重雙假設法(亦有學者稱為多重假令法[6]),而把不含嵌套的雙假設法稱為[一重]雙假設法。

求出x的真值x0以后,斐波那契將其代入比如前兩個方程,得到關于y,z的二元線性方程組

然后第四次運用雙假設法進行求解。此時,他并未使用前述兩個假解(y1,z1)和(y2,z2),而是通過重新設出y的兩個假值y3,y4,得到兩個新的假解(y3,z3),(y4,z4)及其對應的差值,最終求得問題的真解(x0,y0,z0)。綜上所述,斐波那契是通過一次二重雙假設法和一次一重雙假設法而最終求得了上述三元線性方程組的解,過程中總共使用了4次雙假設法。

在《算術實踐概要》中,克拉維烏斯也是運用二重雙假設法求解上述三元線性方程組中x的真值

并且求解程序與斐波那契相同,如圖1所示。但是,在接下來求解y0,z0時,他的做法卻與斐波那契具有重要區別。在求得x0后,對于y0,z0的求解,克拉維烏斯并未像斐波那契那樣將x0代入原三元方程組的兩個方程以得到二元方程組,從而也未第四次運用雙假設法,而是直接利用雙假設法求解公式

得出真解(x0,y0,z0);在上述運算中,相關各量已在求解x0的過程中悉數得到。上述做法表明:(1)求出兩個差值e1和e2之后,每一個未知量都可以由它的兩個假值和這兩個差值通過相同的運算公式解出,因此克拉維烏斯已經發現了雙假設法求解公式的一致性,而斐波那契并未認識到這一點;(2)克拉維烏斯求解三元線性方程組時,僅需運用一次二重雙假設法即可同時求得3個未知量的值,其做法顯然比斐波那契更為簡潔,因為后者通過一次二重雙假設法只求出了一個未知量的值。

1.2 求解公式一致性簡化計算的量化分析

對上述問題, 斐波那契的求解思路如下。 首先將x的假值x1代入比如前3個方程, 可得關于y,z,u的三元線性方程組; 然后利用一次二重雙假設法和一次一重雙假設法求出上述三元方程組的解(y1,z1,u1),即得問題的假解(x1,y1,z1,u1)。 利用同樣的方法, 可得另一個假解(x2,y2,z2,u2), 并且這兩個假解的得出都進行了4次雙假設法的運算。 接下來, 運用第三重(即第9次)雙假設法, 將兩個假解分別代入第四個方程, 得出相應的兩個差值

e1=a4x1+b4y1+c4z1+f4u1-d4,

e2=a4x2+b4y2+c4z2+f4u2-d4;

再根據雙假設法求解公式即得出x的真值x0。 最后, 將x的真值x0代入原方程組中的3個方程, 得到關于y,z,u的三元線性方程組, 并再次進行4次雙假設法運算, 最終得出原問題的真解(x0,y0,z0,u0)。 綜上所述, 斐波那契需要進行13次雙假設法運算才能最終解決這個四元線性方程組的問題。

雖然斐波那契并未表述其所使用的雙假設法可以向n元線性方程組推廣,但通過其求解的各類實例不難看出,他已經意識到多重雙假設法具有一般性,即都是把n元線性方程組的問題歸結為n-1元的問題,如此繼續,一直歸結到二元線性方程組的問題。關于這一點,克拉維烏斯在《算術實踐概要》中并未運用雙假設法求解多于三元的線性方程組,但當問題向n元線性方程組推廣時,他關于雙假設法求解公式一致性的優勢則會表現得更加明顯。例如,對上述四元線性方程組的求解,斐波那契需要進行13次雙假設法的運算,但是克拉維烏斯的解法只需要7次雙假設法的運算。

現將斐波那契與克拉維烏斯求解線性方程組時所需運用雙假設法的次數作以對比,如表1所示。

表1 求解線性方程組所需雙假設法次數統計表

Tab.1 Statistical table of the number of double false position solving linear equations

方程組人 名斐波那契克拉維烏斯雙假設法次數三元a1=4b1=3四元a2=1+3a1=13b2=1+2b1=7五元a3=1+3a2=40b3=1+2b2=15………n元an-2=1+3an-3bn-2=1+2bn-3

同理,根據表1第三列可知,{bn+1}是首項為4,公比為2的等比數列,所以

bn-2=2n-1-1。

綜上可得,對于n元線性方程組,利用克拉維烏斯的方法要比利用斐波那契的方法所節省的雙假設法的運算次數為

l(n)=an-2-bn-2=

這個表達式說明,當n較大時,利用克拉維烏斯關于雙假設法求解公式的一致性可以極大地簡化計算過程,減少了運算量。

2 克拉維烏斯關于雙假設法求解公式一致性的數學原理

克拉維烏斯不僅認識到雙假設法求解公式的一致性,并且明確提出,他的做法比前人更好。在《算術實踐概要》第23章問題2中,克拉維烏斯在運用雙假設法求得x0后,首先采用和斐波那契一樣的直接代入法求得y0，z0,然后利用雙假設法求解公式的一致性同樣求得y0，z0;在問題19中,他提到:

第二個數和第三個數的得出或者是根據雙假設法,用第二個或者第三個假解乘以相應的差值,等等;或者是在第一個數求出后,……,第二、三個數隨之得到(2)Numeros porro hos secundi & tertij inucnics vel cx regula salsi, multiplican do errorcs per secoundi ac tertij positiones, & c. vel ex primo inuento, quemqdmodu Paulo ante ex 100. & 200. quos numeros posuimus primu habere. numeros secundi, ac tertij inuestigauimus. ([4],184-185頁)。

克拉維烏斯很清楚其新方法的優越性。他認為,與前人那種“得到第一個數之后,需將其代入合適的方程,再通過雙假設法求解”的方法相比,他自己的方法更好。

對于克拉維烏斯能同時求得三個未知量的值的做法,亦即其雙假設法求解公式的一致性,《算法史》試圖利用行列式理論給出現代解釋。該解釋首先通過兩次設出假值xi(i=1,2,下同),得到假解滿足的對應三元線性方程組

然后通過克拉默法則推導出xi的表達式,最后聯立兩個假值xi求得真值

但這只能說是推導出了克拉維烏斯雙假設法的求解公式,而并未達到試圖解釋其求解公式的一致性的目的,因此該解釋尚不能令人滿意。

關于求解公式一致性的說明,我們提出可以從雙假設法的幾何原理出發進行探究。其核心思想在于,三元線性方程組

(1)

(2)

(3)

的3個方程(1)，(2)，(3)可以分別表示三維空間中的3個平面π1,π2,π3,因此求解該方程組就相當于求這3個平面的交點P0(x0,y0,z0)。

如圖2所示,設出x的一個假值x1,將其分別代入式(1)和式(2),可得關于y,z的二元線性方程組,運用雙假設法可求得問題的假解(x1,y1,z1),該假解同時滿足前兩個方程,亦即同時在前兩個平面上,因此這個假解是兩平面π1,π2的交線l上的一點P1(x1,y1,z1);同理可得,方程組的另一個假解(x2,y2,z2)是l上的另一點P2(x2,y2,z2)。這樣,P1,P2兩點就確定了兩平面π1,π2的交線l。

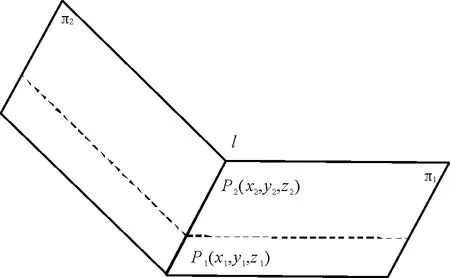
圖2 一重雙假設法示意圖Fig.2 Schematic diagram of double false position

接下來如圖3所示,將假解(x1,y1,z1)代入3)式得,

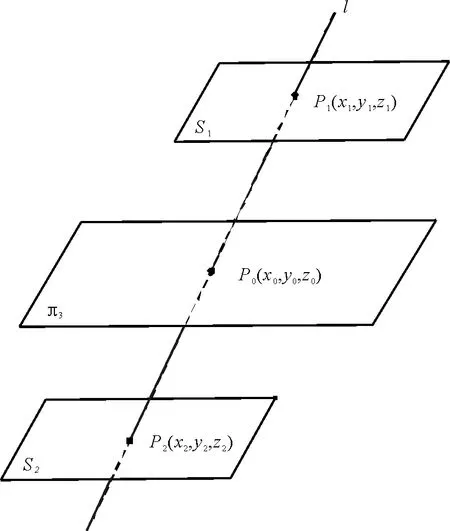
圖3 二重雙假設法示意圖Fig.3 Schematic diagram of twofold double false positions

a3x1+b3y1+c3z1=d3+e1,

這相當于得到了過點P1且平行于π3的平面S1,其中線段P1P0的長度由差值e1決定;同理,將另一個假解(x2,y2,z2)代入式(3)得,

a3x1+b3y1+c3z1=d3+e2,

這相當于得到了過點P2且平行于π3的平面S2,其中線段P0P2的長度由差值e2決定且滿足

而原方程組的解是平面π1,π2的交線l與平面π3的交點P0(x0,y0,z0),通過比例關系

既容易推導出雙假設法求解公式,也容易解釋該求解公式能夠同時求出3個未知量的值,即該求解公式具有一致性。

當雙假設法向n元線性方程組推廣時,仍然可以類似地解釋雙假設法求解公式的一致性,只不過此時平面變成了超平面,直線變成了超直線,點的維度也隨之增加。至此,我們已經成功地解釋了克拉維烏斯雙假設法求解公式一致性的數學原理。克拉維烏斯當然不可能這樣來思考問題,那么他又是如何意識到其求解公式的一致性的?

3 克拉維烏斯發現求解公式一致性的一種可能思路

克拉維烏斯的著作《算術實踐概要》第23章雙假設法中共包含22個問題,其中第2，3，5，19，20這5個問題屬于三元線性方程組的問題,其余17個問題均為二元線性方程組問題。在該章求解過程中,克拉維烏斯運用雙假設法求解公式的一致性簡化了前人的計算步驟,但他只是敘述了其計算程序并輔以具體實例說明,并沒有就其發現求解公式一致性的思路作出說明。我們在表2中總結出他利用一重或二重雙假設法求解這5個三元線性方程組問題的運算過程及相應結果。

這里第2,3,19,20這4個問題都是特殊的三元線性方程組問題,只要知道了一個未知量的值,即可由代入法直接得出另外兩個未知量的值。因此這幾個問題只使用一次雙假設法即可得出真值x0,繼而由代入法可直接得出真值y0,z0。克拉維烏斯在直接代入法之后,又利用其雙假設法求解公式的一致性更加簡潔地求解問題5所代表的一般三元線性方程組。對于克拉維烏斯求解公式一致性的發現,我們認為,他有可能是在對上述4個問題計算求得x0，y0，z0后,觀察到并據此關系式推導得出具有一致性的雙假設法求解公式。事實上,如果他手頭有類似于表2的圖表,那么根據上述的4個例子,是不難發現其求解公式的一致性的。

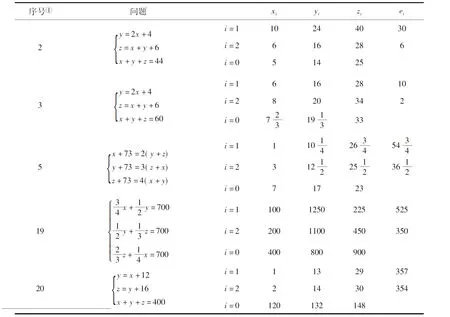
表2 克拉維烏斯的二重雙假設法Tab.2 Twofold double false positions of Clavius

①以《算術實踐概要》第23章問題的先后對應編號。

4 結 語

綜上,我們對比了斐波那契和克拉維烏斯的二重雙假設法的異同,指出斐波那契認識到多重雙假設法的一般性,未認識到求解公式的一致性;而克拉維烏斯則發現了二重雙假設法求解公式的一致性,從而能在很大程度上簡化運算。我們對其簡化運算的效果給出了量化分析,并解釋了克拉維烏斯求解公式一致性的數學原理。進一步,我們分析了克拉維烏斯對5個三元線性方程組問題的詳細計算過程,認為他可能是通過對4個特殊例子的計算結果的分析和歸納,而發現了二重雙假設法求解公式的一致性。