反結構切換混沌系統

顏閩秀，徐 輝

(1.沈陽化工大學信息工程學院，遼寧 沈陽，110142；2.沈陽化工大學工業環境-資源協同控制與優化技術遼寧省高校重點實驗室，遼寧 沈陽，110142)

切換混沌系統由多個子系統組合而成，與模型中只有一個非線性方程組的混沌系統相比，其具有更加復雜的動力學行為和更強的偽隨機性，使得混沌同步保密通信的安全性能大大提高[1-3]。為了使多系統切換混沌同步技術在工程實際中得到更為廣泛的應用，研究人員構建出不同結構的切換系統。文獻[4]將Lorenz系統的第三個方程中的非線性項xy改為x2，同時引入線性反饋項x或y，得到4個混沌子系統來進行自動切換。文獻[5]提出一個含有4個參數、2個非線性項的混沌系統，文獻[6]則將該混沌系統模型中第三個方程的非線性項x2換成xy，得到一個新的子系統，并與原系統實現自動切換。文獻[7]將Chen系統中第三個表達式的二次項分別換成x2、y2平方項得到兩個子系統，并和Chen系統組成自動切換混沌系統。文獻[8]是將文獻[9]提出的模型中第三個方程含有的x2項換成xy和y2，得到兩個新系統和原系統進行三個子系統的自動切換。

上述切換混沌系統都是在已有模型的基礎上，將其中的二次項換成其他形式的二次項，通過改變系統的狀態變量來得到可進行切換的子系統。

本文通過設計切換函數，提出一個新的非自治切換混沌系統，它具有兩個互為反結構的子混沌系統[10]，僅僅通過改變模型表達式系數的正負號來實現兩個子混沌系統的切換，減小了通過改變狀態變量來實現切換的難度以及實際應用中搭建電路的復雜性。下面首先通過理論分析和仿真實驗進行該系統的動力學特性分析，然后設計系統電路并利用Multisim模擬來驗證所提出的新混沌系統的可實現性。

1 系統模型及其特性分析

在提出本文的反結構切換混沌系統之前，首先對兩個子混沌系統A和B作簡要分析。

1.1 子混沌系統A

子混沌系統A的模型為：

(1)

式中：系統參數a=4，b=12.5，c=3，d=2。現給定初始值(0.1，0.1，0.1)，利用Matlab仿真可得系統A的混沌吸引子，如圖1所示。

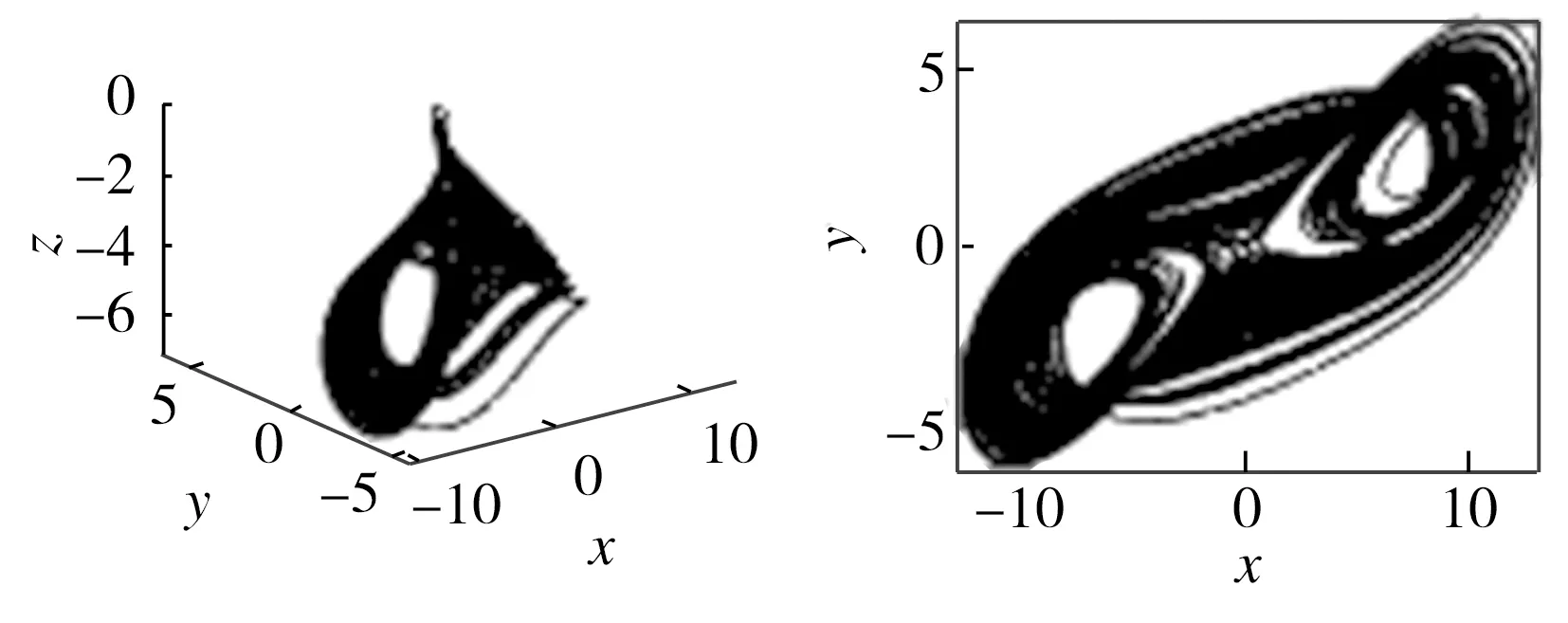
(a)x-y-z三維相圖 (b)x-y平面相圖

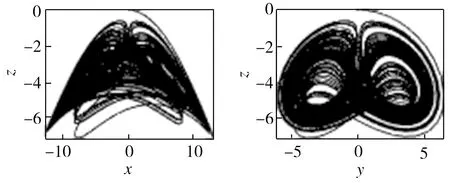
(c)x-z平面相圖 (d)y-z平面相圖

圖1 系統A的吸引子相圖

Fig.1 Phase diagrams of attractors of system A

利用正交法求得系統A的李雅普諾夫指數為：λL11=0.6949，λL12=0，λL13=-3.6949。按式(2)計算系統的李雅普諾夫維數D1L：

(2)

式中：j為滿足下式的最大整數,

(3)

故此處j取2，最終得到：

(4)

系統A的三個李雅普諾夫指數中，一個為正數，一個為零，另一個為負數，且它的李雅普諾夫維數為分數，所以可判斷系統A是一個混沌系統。

1.2 子混沌系統B

子混沌系統B的模型為：

(5)

這里的參數a、b、c、d與混沌系統A的參數相同，不同的是二次項系數的符號與系統A的相反。給定初始值(0.1，0.1，0.1)，利用Matlab仿真可得系統B的混沌吸引子，如圖2所示。

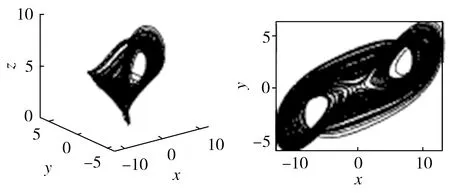
(a)x-y-z三維相圖 (b)x-y平面相圖

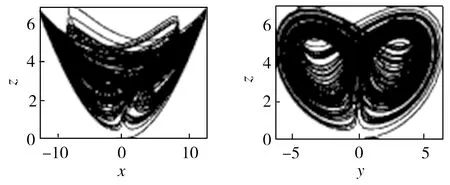
(c)x-z平面相圖 (d)y-z平面相圖

圖2 系統B的吸引子相圖

Fig.2 Phase diagrams of attractors of system B

求得系統B的李雅普諾夫指數為：λL21=0.6821，λL22=0，λL23=-3.6822。計算其李雅普諾夫維數為：

(6)

與系統A類似，可判斷出系統B是一個混沌系統。

系統A和系統B互為反結構混沌系統，從圖1和圖2可以明顯看出二者吸引子的不同，即它們正反顛倒。

下面通過設計簡單的切換函數，將混沌系統A和B構建成一個切換混沌系統，稱為反結構切換系統，并對反結構切換混沌系統的吸引子及其一般特性進行分析。

1.3 反結構切換混沌系統模型

本文提出的新型反結構切換混沌系統模型為：

(7)

式中：系統參數仍為a=4，b=12.5，c=3，d=2；f是所設計的切換函數，其表達式為：

(8)

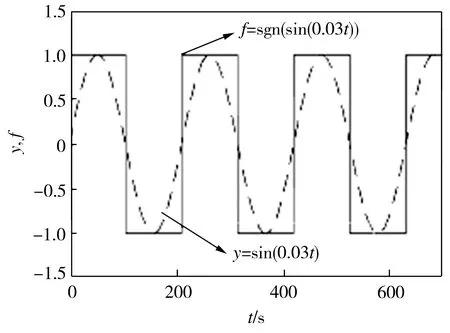
圖3 正弦函數和切換函數的圖像

Fig.3 Graphs of sinusoidal function and switching function

切換函數f的功能就是通過改變系統模型二次項系數的符號來實現兩個子系統的切換。從圖3中可知：在第一個0.5T內f=1，切換混沌系統先以子系統A的模型運行；在第二個0.5T內f=-1，切換混沌系統以子系統B的模型運行。如此反復切換運行。

給定初始值(0.1，0.1，0.1)，利用Matlab仿真得到反結構切換系統(7)的吸引子，如圖4所示。

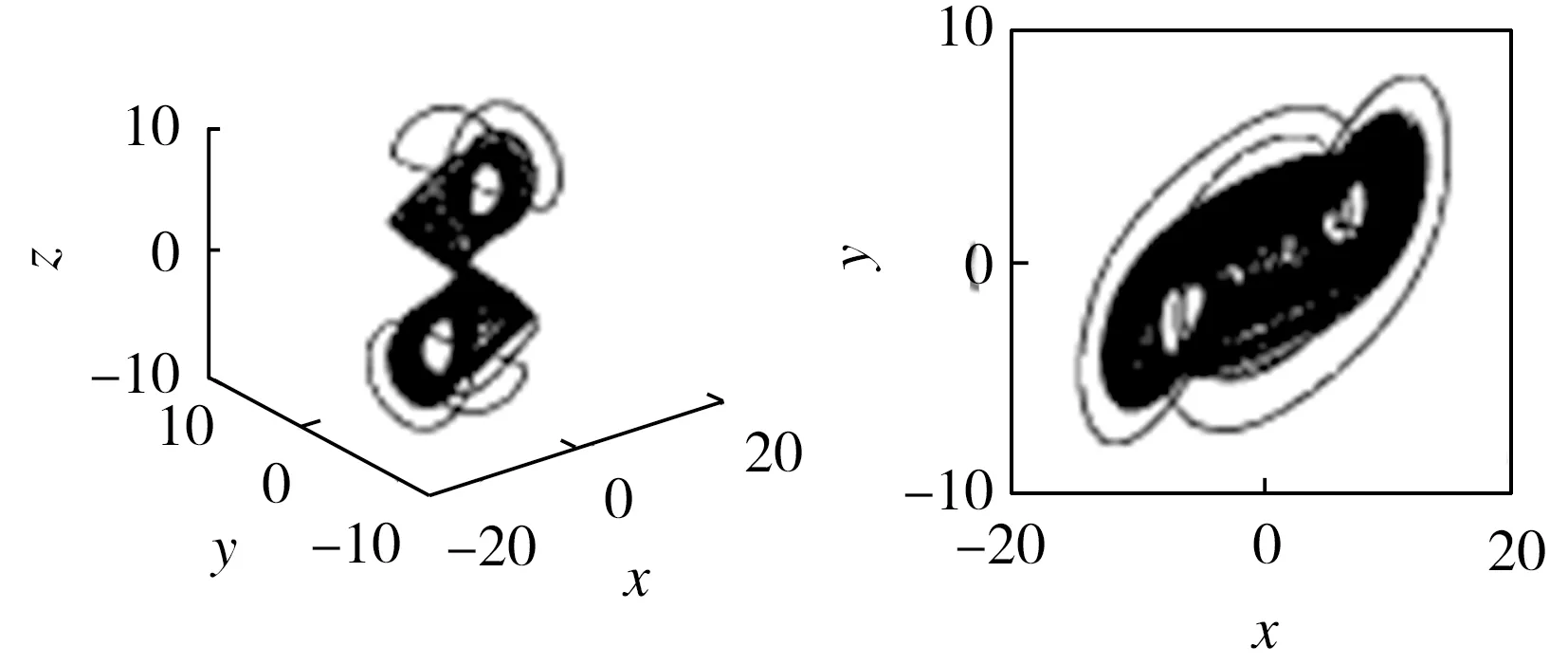
(a)x-y-z三維相圖 (b)x-y平面相圖

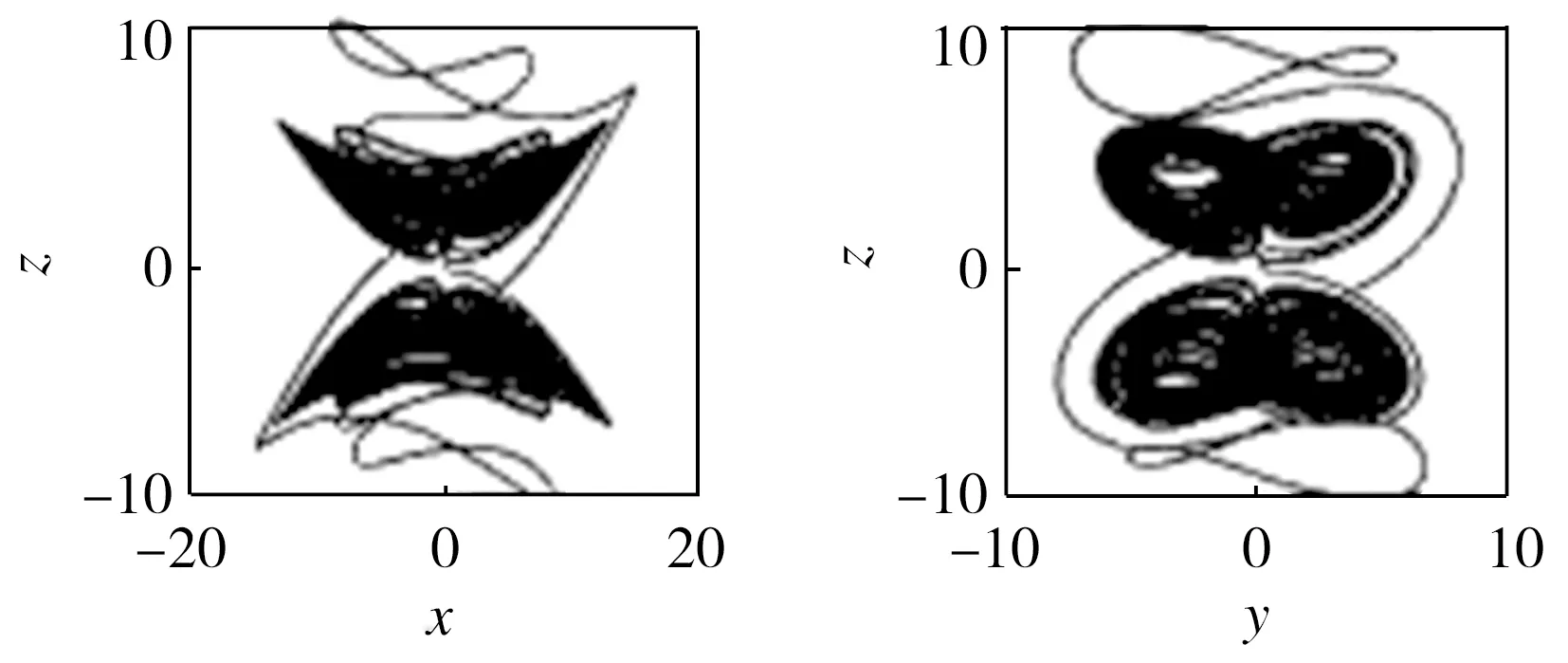
(c)x-z平面相圖 (d)y-z平面相圖

圖4 切換系統的吸引子相圖

Fig.4 Phase diagrams of attractors of the switchable system

從圖4可以清楚看出，切換系統的吸引子是有界的，其首先以系統A的模型運行，形成下半部分吸引子；當運行至半個周期結束時，下半部分吸引子產生一條連續的脫離軌跡線來切換至系統B，從而產生上半部分吸引子；當一個周期運行結束時，上半部分吸引子產生一條連續的脫離軌跡線來進行下一次切換運行。

1.4 切換系統的耗散性及其吸引子存在性

-a+c-d=-3

(9)

(10)

上式表明，當t趨于無窮時,包含系統軌跡的每個體積元均以指數級速率收縮到零，這證明了系統吸引子的存在性。

1.5 切換系統的混沌性

采用正交法得到切換系統的李雅普諾夫指數為：λ1=0.6963，λ2=0，λ3=-3.6784。時間變化時的李雅普諾夫指數譜如圖5所示，可見隨著時間的演化，系統的3個李雅普諾夫指數都趨于一固定常數。

根據式(2)得到反結構切換系統的李雅普諾夫維數DL=2.1893。該系統具有正、負、零三個李雅普諾夫指數，且李雅普諾夫維數為分數，可判定它是混沌系統。

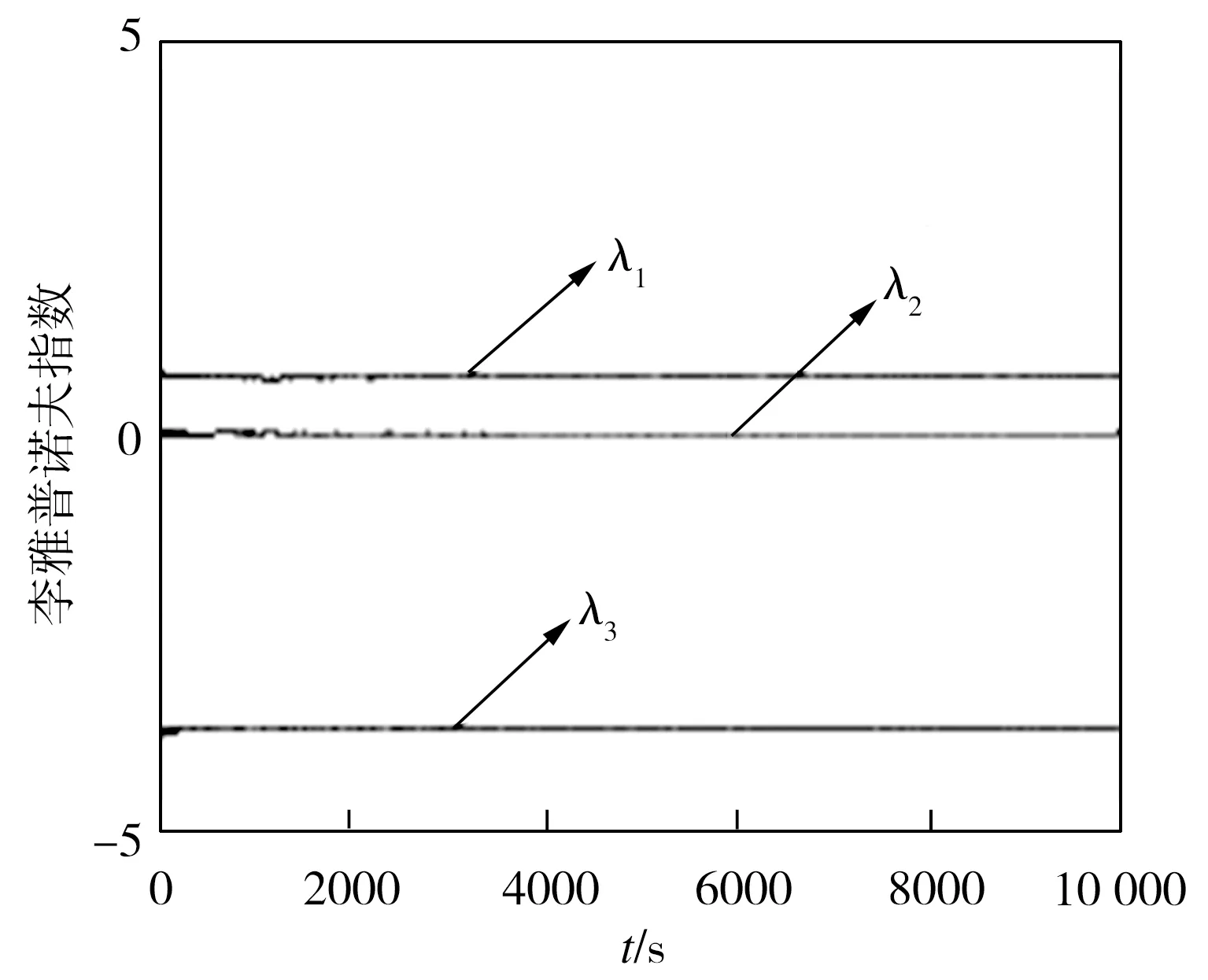
圖5 時間變化時的李雅普諾夫指數譜

Fig.5 Lyapunov exponential spectra with the variation of time

1.6 切換系統的平衡點及其穩定性

由于切換混沌系統是系統A和系統B經切換函數聯結構成，所以它的平衡點也是由系統A和B的平衡點組成。

令系統A的模型式(1)等號左邊為0，得到：

(11)

解得系統A的平衡點為：A1(0，0，0)，B1(-8.795，-2.814，-3.96)，C1(8.795，2.814，-3.96)。

在點A1(0，0，0)線性化得到Jacobian矩陣為：

(12)

解得其特征值為6.553、-2、-7.553，因其有兩個負實根、一個正根，所以平衡點A1為系統的不穩定鞍點。采用類似方法可判定B1、C1點為系統的不穩定鞍焦點。

令系統B的模型式(5)等號左邊為0，得到：

(13)

解得系統B的平衡點為：A2(-8.795，-2.814，3.96)，B2(0，0，0)，C2(8.795，2.814，3.96)。

在平衡點A2(-8.795，-2.814，3.96)線性化得到Jacobian矩陣為：

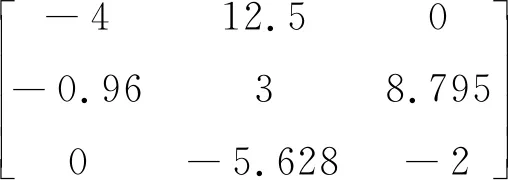
(14)

解得其特征值為0.3348-7.338i、0.3348+7.338i、-3.67，因其有一個負實根、兩個實部為正的共軛復根，所以A2點為系統的不穩定鞍焦點。采用類似方法可判定B2點為系統的不穩定鞍點、C2點為系統的不穩定鞍焦點。

綜上所述，系統的所有平衡點均是不穩定的。

1.7 切換系統關于的分岔圖和李雅普諾夫指數譜

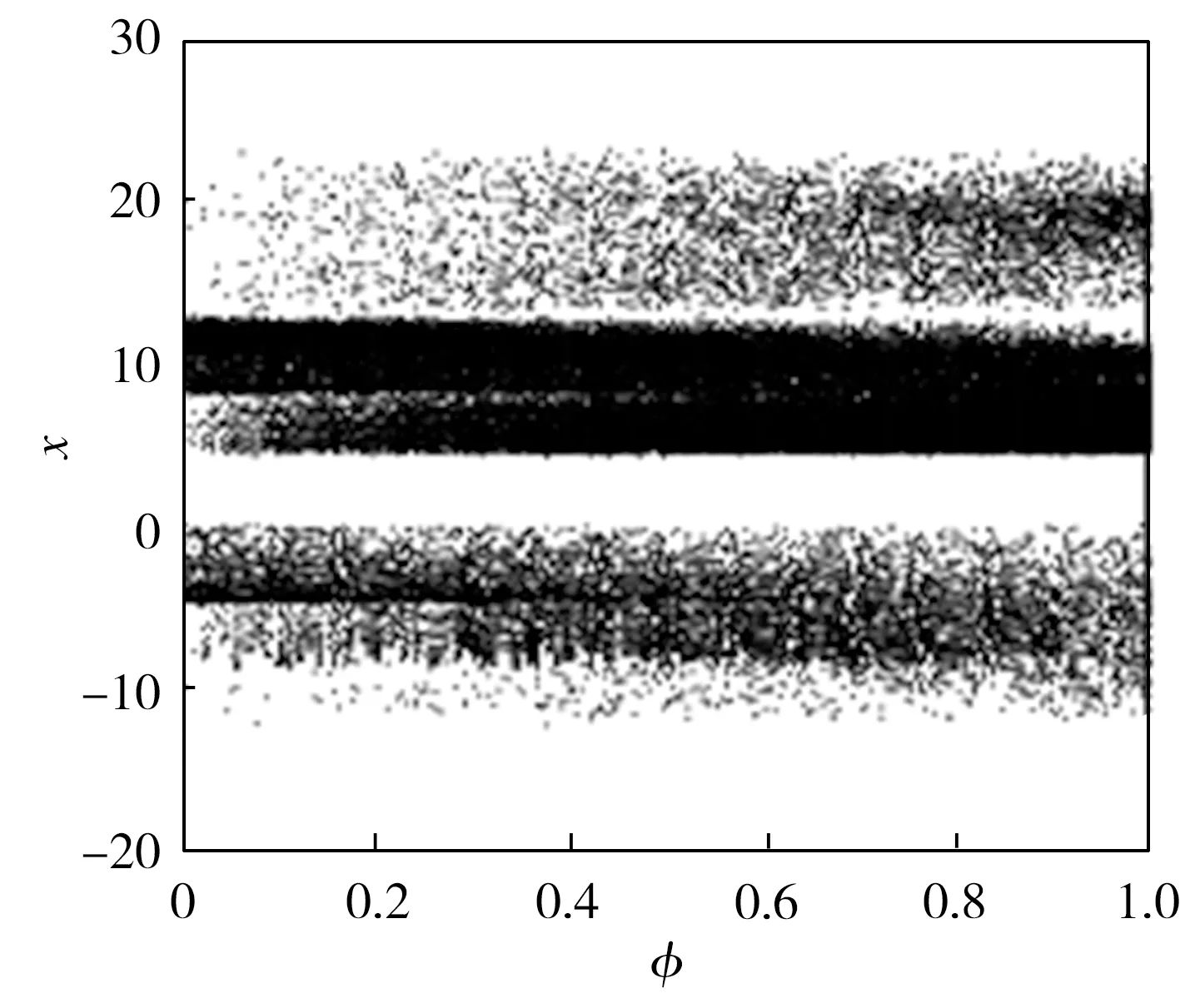
圖6 參數變化時的分岔圖

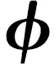
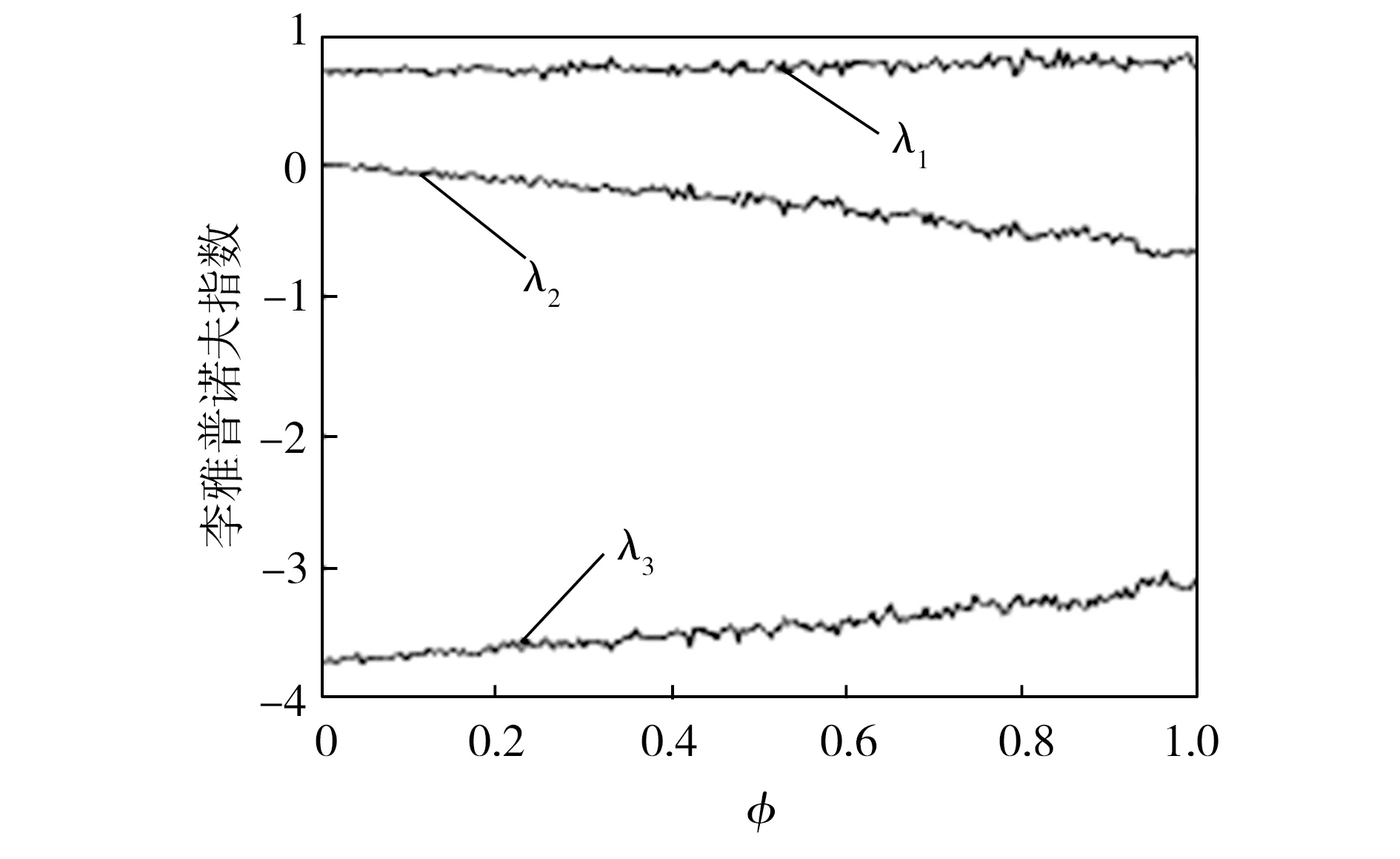
圖7 參數變化時的李雅普諾夫指數譜

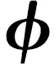
1.8 切換系統的龐加萊截面和功率譜

為了分析切換系統的動力學特性，利用Matlab軟件繪制其功率譜和龐加萊截面圖。

圖8(a)為切換混沌系統關于變量y的功率譜，圖8(b)～圖8(d)分別為xy平面關于z=-3、yz平面關于x=0、xz平面關于y=1的龐加萊截面圖。

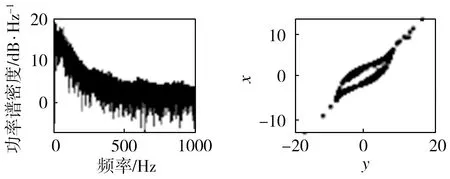
(a)功率譜 (b)龐加萊截面(z=-3)

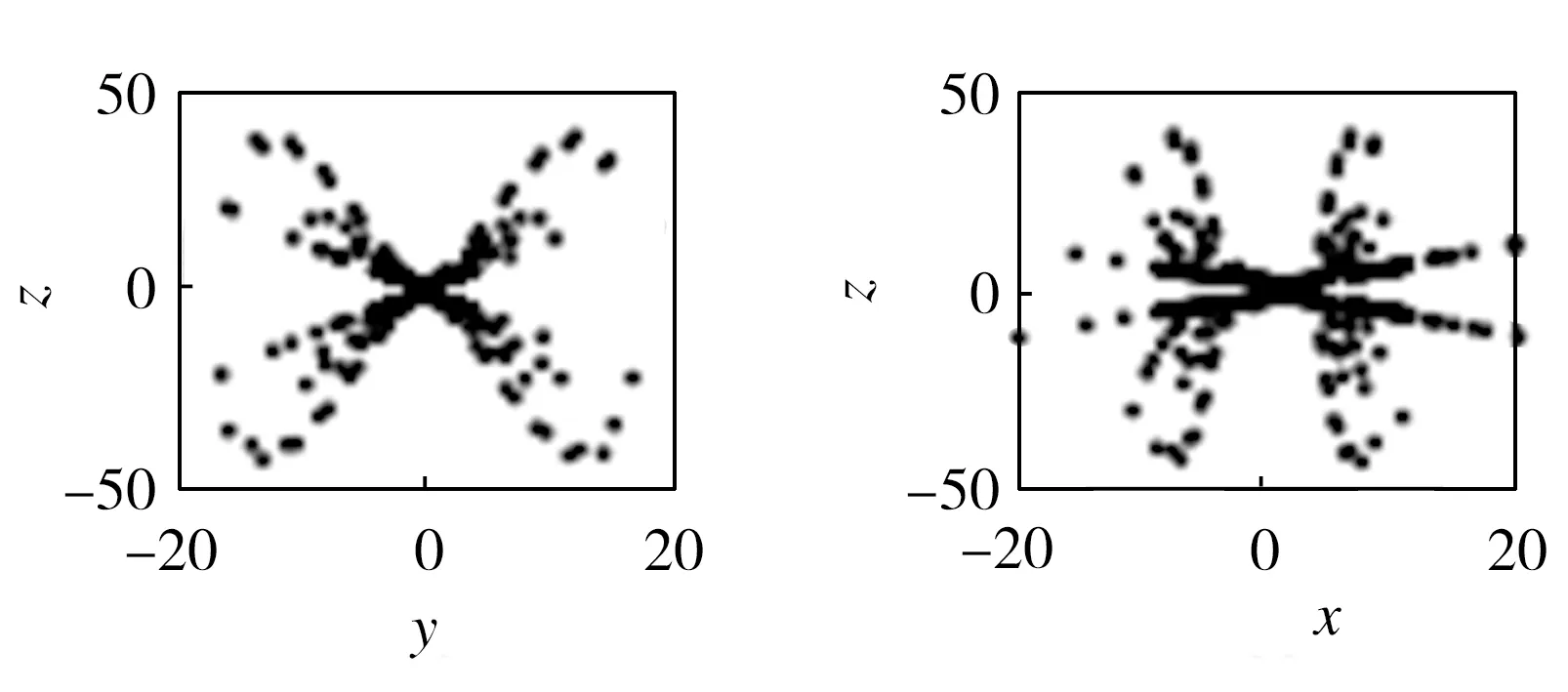
(c)龐加萊截面(x=0) (d)龐加萊截面(y=1)

圖8 功率譜及龐加萊截面圖

Fig.8 Power spectrum and Poincaré sections

從圖8可以看出，系統的功率譜是連續譜，沒有明顯的波峰，而龐加萊截面圖并非一條封閉的曲線，吸引子的葉片明顯可見，進一步表明該切換系統是混沌系統。

2 切換混沌系統的電路設計

通過設計模擬電路來判斷本文提出的切換混沌系統能否實現，并對上述理論分析和仿真結果進行驗證。圖9為所設計的系統電路原理圖，其中，用脈沖電壓源實現切換混沌系統的切換函數功能，兩個脈沖電壓源的內部值設置相同，如圖10所示。

根據電路原理得到混沌電路的實現方程為：

(15)

將式(15)與式(7)對比，可得：

(16)

以式(16)為約束條件，取值如下：

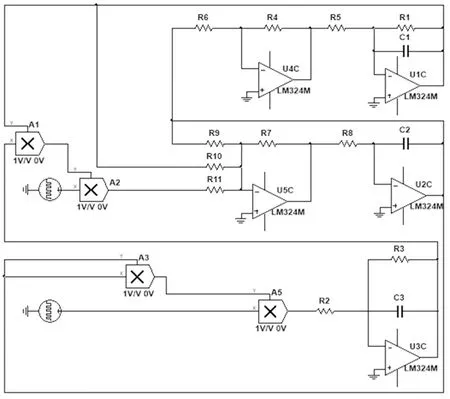
圖9 切換混沌系統電路圖

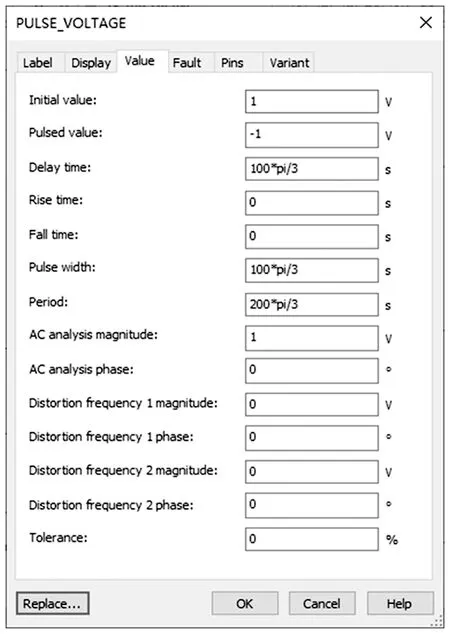
圖10 脈沖電壓源的參數設置

(17)

從圖11～圖13可以看出，電路模擬結果與Matlab數值仿真的結果一致，表明本文提出的切換混沌系統能夠通過實際電路實現。

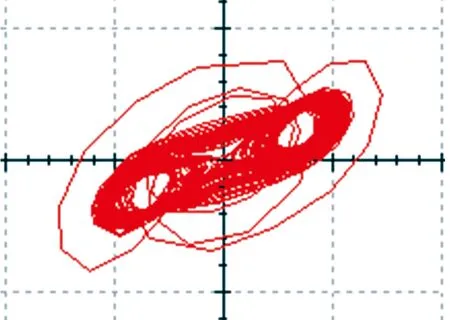
圖11 U1-U2相圖

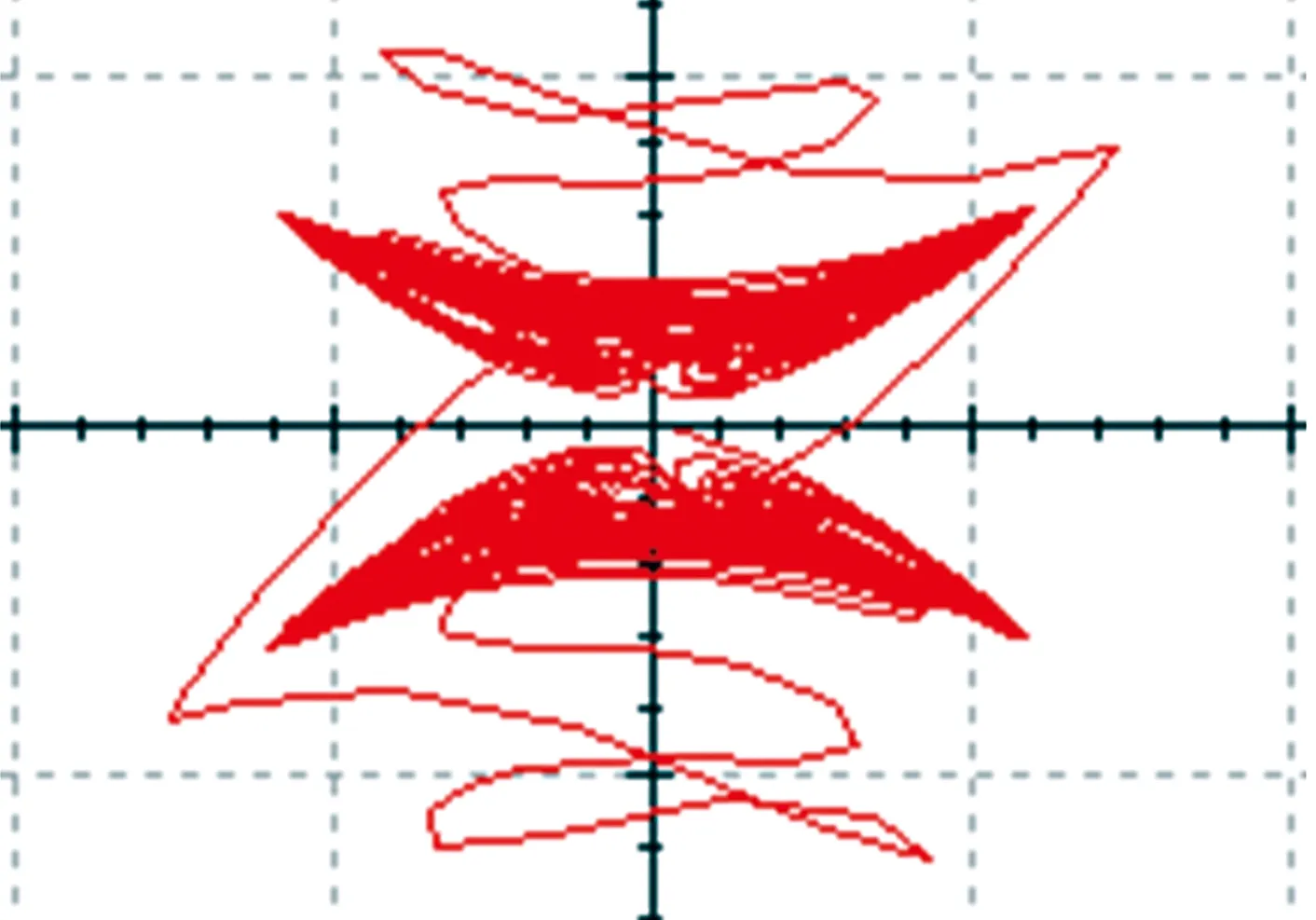
圖12 U1-U3相圖

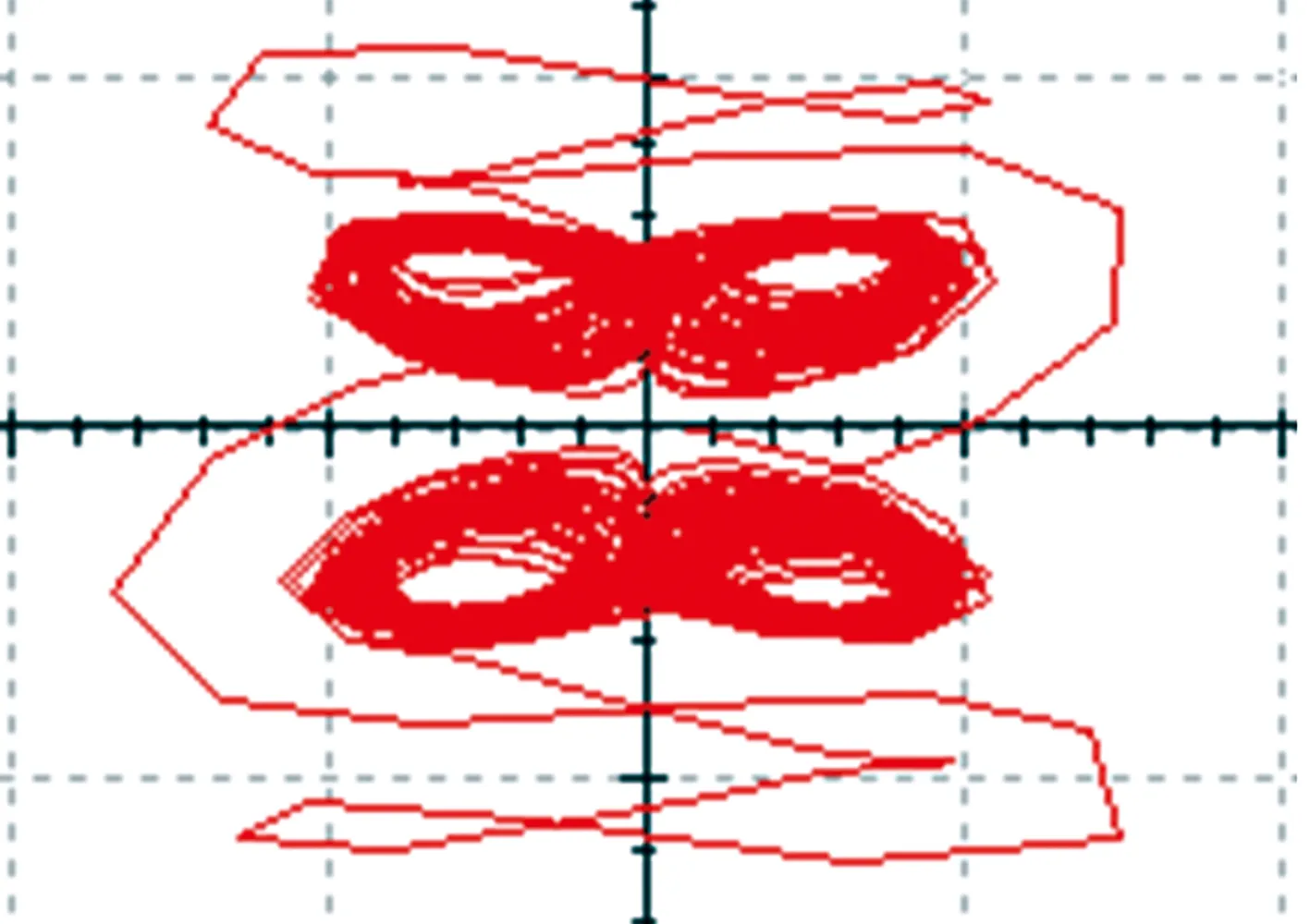
圖13 U2-U3相圖

3 結語

本文設計出切換函數，將兩個互為反結構的子混沌系統組成一個新的自動切換混沌系統。通過理論計算和Matlab仿真，利用李雅普諾夫指數和維數、分岔圖、功率譜、龐加萊截面、平衡點的穩定性等途徑對該系統的動力學特性進行分析，并根據混沌系統模型搭建了模擬電路。電路模擬結果與理論計算和Matlab數值仿真結果一致，證實該切換混沌系統可以電路實現。