讓學生在“玩”的過程中“再創(chuàng)造”數(shù)學

李紅霞

[摘? ?要]有效的數(shù)學活動不能單純地依賴模仿與記憶，應是在教師的引導下由學生本人把要學的東西去發(fā)現(xiàn)或創(chuàng)造出來.讓學生在“玩”中理解并獲得數(shù)學知識，不僅可以培養(yǎng)學生的學習興趣，也是培養(yǎng)學生“再創(chuàng)造”能力的有效途徑.

[關鍵詞]再創(chuàng)造;玩;旋轉;三角板;復習課

[中圖分類號]? ? G633.6? ? ? ? [文獻標識碼]? ? A? ? ? ? [文章編號]? ? 1674-6058（2019）29-0012-04

一、問題的提出

在一節(jié)《認識三角形》的復習課中，授課教師先在大屏幕上出示一個三角形，并說道：“我們已經(jīng)學習了三角形的有關知識.”接著告訴學生：“今天我們要學習的內(nèi)容有：對于任意一個三角形，按角分，可得到哪些性質？按邊分，又可以得到哪些性質？在特殊三角形中，又可以進行怎樣的分類？”縱觀整節(jié)課，教師對教材內(nèi)容、難易度的把握都很到位，并且知識分類也很明確;期間，學生的回答也比較熱烈，也能很認真地完成練習.應該說是一堂很不錯的復習課，但是筆者總感覺少了點什么.

荷蘭數(shù)學家、教育家弗賴登塔爾認為，學習數(shù)學的唯一正確的方法是實現(xiàn)再創(chuàng)造，也就是由學生把本人要學習的東西自己去發(fā)現(xiàn)或創(chuàng)造出來，教師的任務是引導和幫助學生去進行這種再創(chuàng)造工作，而不是把現(xiàn)成的知識灌輸給學生.本節(jié)復習課，始終是教師在講，學生在聽，所有的知識歸納、條理分析均是教師組織的，學生一切聽從教師的指揮，根本沒有“權利”去再發(fā)現(xiàn)、再創(chuàng)造，其主觀能動性得不到彰顯.這樣的課，教師“教”得再好，學生得到的知識也是“死”的，學生是憑記憶而“學會”了，而不是“會學”了，更談不上“再創(chuàng)造”.

那么，怎樣的數(shù)學活動才是有效的？

筆者認為，有效的數(shù)學活動不能單純地依賴模仿與記憶，動手實踐、自主探索與合作交流應成為學生學習數(shù)學的重要方式.教師的任務是引導和幫助學生在“玩數(shù)學”的過程中去進行再創(chuàng)造.

二、“再創(chuàng)造”理論的具體應用

荷蘭數(shù)學家、教育家弗賴登塔爾的數(shù)學教育思想主要有：強調數(shù)學教育面向社會現(xiàn)實，必須聯(lián)系生活實際，注重培養(yǎng)和發(fā)展學生從客觀現(xiàn)象發(fā)現(xiàn)數(shù)學問題的能力;用再創(chuàng)造的方法去進行教學，反對灌輸式和死記硬背;提倡討論式、指導式的教學形式，反對傳統(tǒng)的講演式的教學形式.他提出的這一“再創(chuàng)造”理論不是“教育學+數(shù)學例子”式的論述，而是要求教師抓住數(shù)學知識的規(guī)律、特征，給學生創(chuàng)建一個“再創(chuàng)造”的通道，引導學生通過操作、推理、猜想、歸納、類比等方式，緊扣數(shù)學教育的特殊過程來獲取知識.

下面是教師借助平時常用的一副三角板，在一堂數(shù)學復習課中演繹出許多“旋轉”中的數(shù)學問題，并促使學生沉浸在嚴謹、美妙的數(shù)學問題的解決過程中實施探究、再創(chuàng)造.

（一）依據(jù)“數(shù)學現(xiàn)實”創(chuàng)設情境，發(fā)現(xiàn)問題

對于弗賴登塔爾所提出的“數(shù)學現(xiàn)實”，筆者認為應該包括以下三類客觀現(xiàn)實：第一，包含教材當中需要學習的知識體系這一現(xiàn)實;第二，包含學生對所學知識的前后關聯(lián)及掌握程度與學生對知識的理解能力這一現(xiàn)實;第三，包含數(shù)學課程標準提出的教學目標、要求等這一現(xiàn)實.教師在課堂上創(chuàng)設情境，就是把這些客觀現(xiàn)實與知識體系融為一體，在以問題為導向的教學情境中搭建數(shù)學“再創(chuàng)造”的平臺，著眼于學生“再創(chuàng)造”能力的培養(yǎng).

1.依據(jù)“數(shù)學現(xiàn)實”創(chuàng)設教學情境

教師課前準備教具：一副三角板、與三角板大小一樣的三角形紙片、投影機.

師：這節(jié)《認識三角形》的復習課，我們離開書本一起來玩一下三角板.談起三角板，大家會覺得特別熟悉和親切，因為它是我們學習數(shù)學的好幫手.它可以畫線段，量長度，畫平行線，甚至可以畫特殊角，但很少有同學把一副三角板組合在一起用，其實它里面蘊含了大量的數(shù)學知識，今天就讓我們一起去揭開它神秘的面紗，探索它的奧秘.

課始，教師創(chuàng)設新穎別致的情境，讓學生“玩”三角板，給學生營造了輕松愉快、生動活潑的學習氛圍，激起了學生的學習興趣，同時又指出“三角板里面蘊含了大量的數(shù)學知識，要探索它的奧秘”，這在激發(fā)學生求知欲的同時提醒他們要自己進行知識探究.

2.結合“數(shù)學現(xiàn)實”引發(fā)數(shù)學問題

接著，教師依據(jù)學生的現(xiàn)實水平，在激發(fā)學生學習興趣的前提下提出問題.

師（拿出含45°角的直角三角板并舉起來）：仔細觀察，這塊三角板有什么樣的特點？

生1：它是等腰直角三角形，有一個直角，兩個銳角，且都是45°.

師：很好！你講出了角的本質特點，那這塊三角板的角又有何特點呢？（舉起含30°角的直角三角板）

生2：它是直角三角形，有一個直角，兩個銳角，一個是30°，另一個是60°.

師（旋轉一下，變化位置）：此時的角度呢？邊的長度呢？

生3：角度還是沒變，分別是30°、60°、90°.對應邊的長度也沒變.

師：把一個圖形進行旋轉，圖形的位置改變，但其角度的大小并沒有變化.

數(shù)學復習課中，教師結合學生的現(xiàn)實思維、知識的掌握程度，由學生熟悉的三角板出發(fā)低起點導入.由于是復習課，知識的涉及面比較多，所以很有必要讓學生輕松下來，活潑起來，營造和諧的教學氛圍.在引入時強調“圖形旋轉時，對應角的度數(shù)不變，對應邊的長度也不變”，為學生自主“認識三角形”和探究構建和再創(chuàng)造“旋轉中的三角形”知識體系埋下伏筆.

（二）進入“旋轉”操作，將具體圖形數(shù)學化

從數(shù)學知識發(fā)展的必要依托來看，學生的“再創(chuàng)造”思維的煥發(fā)，既需要學生已有的知識基礎，更需要教師的有效引導，以充滿“數(shù)學原味”的數(shù)學思想來呈現(xiàn)知識，拓展知識，生成新知識，所以教師的主導作用十分重要.

1.依據(jù)導引動手操作，尋求“問題解決”方法

本節(jié)課開始，教師結合學生的學習現(xiàn)狀，由一副三角板引出教學內(nèi)容，引導學生親歷“三角板中的數(shù)學”——旋轉圖形的不變性.

教師設計如下操作活動，引導學生思考探究.

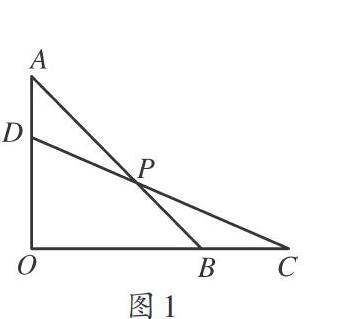
操作1：將一副三角板疊放在一起（圖1），使兩塊三角板的直角頂點重合，兩直角邊也分別重合，你可以知道哪些角的度數(shù)？

學生動手操作，標上字母，逐一回答.這一環(huán)節(jié)，學生有效復習了三角形內(nèi)角和性質、三角形內(nèi)外角的關系等舊知識.

依據(jù)“一副三角板”中的數(shù)學現(xiàn)實，引導學生動手操作，并創(chuàng)設開放性的問題，能有效啟發(fā)學生的數(shù)學思維，使學生靈動地、“數(shù)學化”地構建知識體系，這比教師直接將三角形的知識歸類呈現(xiàn)給學生顯然要有效得多.

操作2：固定含30°角的Rt△COD，將含45°角的Rt△AOB繞O點按順時針方向旋轉，使AO⊥CD，則∠BOD= ? ? ?°，∠AOC=°.（難度系數(shù)是0.92）

此題是前一題知識的具體應用，根據(jù)“三角形內(nèi)角和等于180°”和“圖形旋轉的不變性”即可得到∠BOD=120°，∠AOC=60°.

操作3：將含45°角的Rt△AOB繞O點按順時針方向繼續(xù)旋轉，使AO經(jīng)過斜邊CD的中點，則∠BOD=? ? ? ? °，∠AOC=°.（難度系數(shù)是0.78）

這一題主要用到“直角三角形中斜邊上的中線等于斜邊的一半”這個定理，一般的學生會忘記這個定理.多數(shù)學生會結合前幾題的解題經(jīng)驗，根據(jù)本題的已知條件，得出∠BOD=150°，∠AOC=30°.

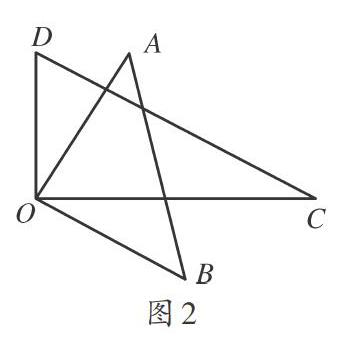
操作4：觀察第2、3題的答案（圖2），猜測在旋轉過程中∠BOD與∠AOC可能有何數(shù)量關系？并證明你的猜想.（難度系數(shù)是0.73）

《義務教育數(shù)學課程標準》指出：“教師應給學生提供充分從事數(shù)學活動的機會，幫助他們在自主探索和合作交流的過程中真正理解和掌握基本的數(shù)學知識與技能、數(shù)學思想和方法.”操作4中的題目變式非常巧妙，是在上面幾題的基礎上進一步深化得到的，是一個只有已知而沒有結論的半開放題，目的是讓學生有充分進行動手操作的機會.對學生而言，具有一定的挑戰(zhàn)性.這就需要學生啟動頭腦中的元認知，自己去思考、探究，構建有目標指向的“數(shù)學化”平臺.

正是鑒于上述課程標準這樣的指導思想，教師留有時間給學生自主思考：根據(jù)圖形旋轉的不變性，可以設∠AOD=α，那么可以得到∠BOD =90°+ α，∠AOC=90°- α，相加可得：∠BOD+∠AOC=180°.

2.深入操作進行探究，將“旋轉圖形”數(shù)學化

前幾個操作題，步步緊扣，圍繞著“繞直角頂點O旋轉”一氣呵成.盡管難度逐漸增加，但是幾乎都是在學生的認知顯然“可以接受”的范圍內(nèi)，學生問題解決的思路順暢.

操作5：讓學生自己進行變式，有學生提出：將含45°角的Rt△AOB繞O點任意旋轉，經(jīng)測得∠BOD=105°， 則∠AOC=°.

盡管學生的變式還是圍繞直角頂點O旋轉，但是已經(jīng)說明學生對前幾個操作題有了比較深刻的理解，能將教師講解的內(nèi)容進行“再創(chuàng)造”.

《義務教育數(shù)學課程標準》提出了學生動手操作在數(shù)學幾何教學中起著重要作用.學生親歷將數(shù)學的實際狀態(tài)演變?yōu)槔碚撔问剑趧邮种蝎@得“再創(chuàng)造”的成就感.

師（將學習內(nèi)容繼續(xù)深化）：交換含45°角的直角三角板與含30°角的直角三角板的位置，引導學生看大屏幕.

實驗操作1：在一副直角三角板中，把含30°角的Rt△DMN的直角頂點與含45°角的Rt△ABC的斜邊中點D疊放在一起.

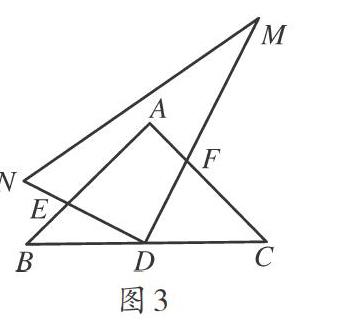
實驗操作2：如圖3，固定含45°角的Rt△ABC，將含30°角的Rt△DMN繞BC的中點D按順時針方向任意旋轉，使直角邊交AB與AC分別為E、F.（1）觀察旋轉過程，哪些線段的長度發(fā)生了變化？如何變化？

（2）試猜想線段AE與CF有何數(shù)量關系？并證明你的猜想. 求證：AE=CF.

（3）通過觀察實驗你有何猜想？請寫出你的猜想結論，并與小組內(nèi)學生合作發(fā)現(xiàn)，交流理由.

在初中數(shù)學中，“圖形旋轉”向來是學生感到比較難理解也難以掌握的內(nèi)容之一，其主要原因是對旋轉后生成的圖形的形狀難以把握;思維不夠縝密，經(jīng)常遺漏題中的隱含條件.本節(jié)課中，教師讓學生自己動手操作，使學生在動手操作的過程中領悟了“圖形旋轉”中的數(shù)學化思想.這樣的教學程序是完全有效的.

本課題的拓展，真正體現(xiàn)了這樣的教學理念：通過學生的動手實踐、自主探索與合作交流，實現(xiàn)學生數(shù)學學習的“再創(chuàng)造”.對于（3），通過學生的操作、猜想、交流，得出的結論很多，如：BE=AF、AE=CF、BE+AE=AE+AF=AB=AC（不變）、∠BDE+∠CDF=90°、∠AFD=∠BED、四邊形AEDF的面積等于Rt△ABC面積的一半、DE=DF等.其關鍵是添加輔助線，連接AD，證明△ADE≌△CDF后就可以得出上述結論.

學生通過動手操作和合作探究能得到“旋轉三角板”中“變”與“不變”的辯證關系，通過“圖形的旋轉”整理成“等”與“不等”的數(shù)學關系.

3.在“互動協(xié)作”中領悟，培養(yǎng)“再創(chuàng)造”思維

猜測、探索是學生“再創(chuàng)造”的前提.正因為本節(jié)課的教學中，教師為學生提供了充分的動手操作的空間，所以學生在體驗“自主、合作、探究”的學習方式的同時，也獲得了生動活潑的、主動而富有個性的發(fā)展，奠定了“再創(chuàng)造”學習的基礎.

學生提問，操作變式：若含30°角的Rt△NDM繼續(xù)繞△ABC斜邊的中點D按順時針方向旋轉（如圖4），使它的兩條直角邊分別與BA、AC的延長線交于E、F，則AE=CF還成立嗎？

師：試試看，AE=CF是不是還成立.

鑒于前幾題的解題經(jīng)驗，有學生提出：連接AD，利用三角形全等的ASA定理證△ADE≌△CDF，得出AE=CF仍成立.

（三）深入導引反思，實現(xiàn)“再創(chuàng)造”

弗賴登塔爾所論述的“再創(chuàng)造”形式，其核心要義就是“教學過程”的再現(xiàn);它并不是簡單地要求學生自己去把所學的東西發(fā)現(xiàn)或創(chuàng)造出來，而是要求教師引導和幫助學生去進行這種再創(chuàng)造的工作.也就是說，學生的“再創(chuàng)造”必須在教師導引的基礎上去實現(xiàn).

1.導引學生回顧、反思，創(chuàng)建“再創(chuàng)造”通道

在經(jīng)過前面的動手操作、演練后，教師要求學生反思本節(jié)課的整個學習過程及“三角板旋轉”中的數(shù)學知識：

① 通過一副三角板，回顧了三角形中邊、角之間的等量關系.

② 通過三角板的旋轉，明確了從中蘊含的等量、不等量關系，及其關鍵是找兩個三角形全等.

③ 通過動手操作、合作探究，學會了根據(jù)條件如何編題，提升了“再創(chuàng)造”的思維和能力.

實踐證明，在初中數(shù)學幾何教學中給學生以充分的動手操作機會，其作用是舉足輕重的.教師要善于導引，使學生從動手操作中理解并獲得數(shù)學知識.通過教師的及時指導引發(fā)學生的反思，更為學生指明了操作過程中的重點、難點與關鍵點，使學生在“做數(shù)學”的過程中打通“再創(chuàng)造”的通道.

2.依據(jù)“數(shù)學化”現(xiàn)實，實施“再創(chuàng)造”

上述操作及練習的設計比較貼近學生的數(shù)學現(xiàn)實，由復現(xiàn)到變式，由模仿到創(chuàng)新，整個教學程序有利于訓練學生的發(fā)散性思維，培養(yǎng)學生的“再創(chuàng)造”能力.接著，教師又針對性地提出了“再創(chuàng)造”要求.

師：你還有另外的旋轉方法嗎？例如改變一下旋轉中心.

學生：（實驗操作）把兩塊三角板的位置交換一下（如圖5），將含45°角的Rt△MDN的直角頂點D點與含30°角的Rt△ABC斜邊BC上的高AD（垂足為D點）重合，并將含45°角的Rt△MDN繞點D按順時針方向任意旋轉，使直角邊與AB、AC交于E、F.①試問∠AED與∠CFD有何數(shù)量關系？請說明理由;②已知DE與DF存在比例關系，試求[DEDF]的值.

本題是在前一題“繞斜邊中點旋轉”的基礎上變式而來的，但是它對于學生而言是一個不小的“創(chuàng)造”.前幾個操作題是利用“三角形全等”將實際問題“數(shù)學化”，而本“數(shù)學化”操作題的研究已經(jīng)用到了“三角形相似”.

三、小結反思

（一）課堂教學架構體現(xiàn)了弗氏“再創(chuàng)造”理論

在本節(jié)課中，教師充分把握學生動手操作的時機，主要體現(xiàn)在：一是依據(jù)學生的數(shù)學現(xiàn)實創(chuàng)設教學情境，設疑加鼓勵，引導學生操作實踐，激發(fā)他們的學習興趣;二是抓住教學機會，引導學生隨時動手操作.在解決問題的同時使學生對操作中得到的規(guī)律形成“數(shù)學化”思想;三是創(chuàng)設現(xiàn)實情境，提供給學生自主探究的空間，讓學生在“玩數(shù)學”的過程中培養(yǎng)“再創(chuàng)造”的能力.

具體架構是：

教師抓住數(shù)學知識的教育特征，給學生創(chuàng)建一個“再創(chuàng)造”的通道，引導學生通過操作、推理、猜想、歸納、類比等，緊扣數(shù)學教育的特殊過程來獲取知識.課堂教學架構體現(xiàn)了弗氏“再創(chuàng)造”理論的實踐.

（二）操作題呈現(xiàn)方式有利于學生“再創(chuàng)造”能力培養(yǎng)

本節(jié)課的教學過程呈現(xiàn)了三種形式的操作練習：

（1）復現(xiàn)操作練習，即單純的模仿性練習，訓練學生思維的流暢性.

（2）變式操作練習，即改變某一知識的非本質屬性，而不改變其本質屬性的練習，鍛煉學生思維的靈活性，為學生的“再創(chuàng)造”奠定基礎，提供通道.

（3）延伸操作練習，即進一步將問題向縱深發(fā)展的練習，是給學生通過“做數(shù)學”而學會數(shù)學的“再創(chuàng)造”.

其設計遵循了“復現(xiàn)——變式——延伸”的原則，符合學生的認知規(guī)律.

操作題的呈現(xiàn)，有目的地循序漸進，從觀察到動手操作實踐，符合學生已有的經(jīng)驗、心理發(fā)展規(guī)律以及所學內(nèi)容的特點，有利于培養(yǎng)和發(fā)展學生的“再創(chuàng)造”思維和能力.

通過“圖形的旋轉”操作來幫助學生改變思維方式.通過一副三角板的旋轉觀察及學生自身對旋轉后的圖形的實踐探索，及與同學的合作交流，讓學生經(jīng)歷知識獲得的全過程，有助于學生自己對幾何知識的理解;通過一副三角板的旋轉觀察，給了學生從不同角度全面認識圖形的變化規(guī)律的時空，使學生學會舉一反三，實現(xiàn)“再創(chuàng)造”學習.

（三）體現(xiàn)了“人人有所得”的教學理念

數(shù)學實踐操作活動要同學生的“數(shù)學現(xiàn)實”緊密結合，需要調動學生參與的積極性.本節(jié)課中，教師引導學生在“三角板的旋轉”操作中步步深入，便于學生聯(lián)系自身的“最近發(fā)展區(qū)”，既獲得數(shù)學學習的經(jīng)驗，又了解三角形旋轉過程中的變化規(guī)律.在“三角板的旋轉”的教學中，每次三角板的旋轉變化都能安排不同量的圖形展示與問題呈現(xiàn)，且有重點、有選擇地運用旋轉出現(xiàn)問題，這對于促進學生掌握解決數(shù)學問題的思想與方法，培養(yǎng)學生“舉一反三”的“再創(chuàng)造”能力大有裨益 .

在本節(jié)課的教學中，教師不斷滲透相關的數(shù)學思想方法，加強數(shù)學思想方法的訓練，讓學生不僅能聽懂，還能領悟，能觸類旁通，深刻理解其中的數(shù)學本質和思想;教師還善待學生的想法，精心地“把脈診治”，使“人人有所得”，使學生能自我實現(xiàn)對數(shù)學知識的“再創(chuàng)造”.

[? 參? ?考? ?文? ?獻? ]

[1]? 中華人民共和國教育部.全日制義務教育數(shù)學課程標準（實驗稿）[S].北京：北京師范大學出版社，2001.

[2]? 龔輝斌.凸顯數(shù)學概念的思維價值[J].中學數(shù)學教學參考，2010（10）：5-8.

[3]? 方勤華.教好數(shù)學的一個重要視角[J].數(shù)學通報，2010（1）：34-37.

（責任編輯 黃春香）