一種航母甲板作業快速調度算法

朱興動，范加利，王 正，趙宏強

(1.海軍航空大學，山東 煙臺 265200；2.海軍航空大學 青島校區，山東 青島 266041)

0 引 言

艦載機在航母甲板上的起降一般分波次循環進行，按循環方式分單周期、雙周期等，循環間隔受艦載機制空時間影響，美軍歷次演習證明，航母航空保障作業中，雙周期循環出動能夠提高艦載機的出動強度，而雙周期連續出動的制約因素主要在于艦載機制空時間和艦載機再次出動準備時間的匹配。在循環出動模型下，留給艦載機進行再次出動準備的時間非常有限，美國海軍1997 年對尼米茲級航母進行高強度出動演習表明，當循環周期為1 h 45 min 時，平均可用甲板作業時間僅為57 min。因此，在艦載機和航母設計定型后，如何優化配置和合理安排批次艦載機的再次出動保障工作對于提高航母艦載機出動強度的提高具有非常重要的意義。

受作業完成時間的不確定性、艦載機及保障裝設備故障的隨機性、作業環節的多態性等因素的影響，涉及多架艦載機、多種保障資源的艦載機再次出動作業的調度問題屬于典型的動態調度問題。近年來，國內學者在該領域進行了大量的研究工作，針對該問題常用的方法是建模仿真方法[1-2,6]、最優化方法[3]，以及基于專家方案的逆向強化學習方法等[4]。但多數文獻中仍以靜態調度為研究基礎[5,7]，通過提高調度結果的魯棒性和自適應性來增強調度系統（算法）對動態、隨機環境的響應能力，避免頻繁重調度。基于仿真的研究方法計算時間偏長，對于實時重調度的適應能力較弱。

圖 1 艦載機再次出動準備作業時序Fig.1 The sequence diagram of carrier aircraft turnaround operations

針對航母艦載機甲板航空保障作業的調度問題，本文在對調度作業指揮人員實際需求分析的基礎上，重點研究了雙周期出動模式下艦載機再次出動準備的調度問題，建立了艦載機再次出動準備的優化計算模型，并設計一種適用于動態甲板環境的基于啟發式禁忌搜索的快速求解算法，最后以庫茲涅佐夫航母上8 機雙周期再次出動準備作業為例進行驗證。

1 艦載機再次出動保障任務調度模型

1.1 艦載機甲板作業描述

俄羅斯 “庫茲涅佐夫” 航母是一種采用滑躍方式起飛的中型航母，通常搭載蘇-35 飛機作為主戰艦載機。航母設計階段，通常將飛行甲板分為若干功能區域，并在各區域設置多個站位，受空間及站位配置資源的限制，“庫茲涅佐夫” 航母上，艦載機著艦后必須先滑行至臨時停機位，而在起飛前則必須牽引至暖機位進行慣導對準、暖機、飛控系統自檢等作業，隨后依次滑行至起飛位起飛。艦載機再次出動準備的作業流程如圖1 所示。

對于任一架艦載機，圖中作業集 TS1中的加油、掛彈和牽引至暖機位作業的執行順序可任意調換，但受技術和管理性約束，對于某一架飛機這3 項作業不能同時進行； 作業集 TS2中的慣導對準、 暖機、 滑行、起飛任務必須依次執行；再次出動機務檢修（飛機后的檢修、視情添加輔助油料、充氧充氮等）作業可與作業集 T S1和 T S2中的部分作業并行執行。

上述諸多作業中按照對甲板資源的需求類型可分為特定甲板資源、不定甲板資源和無需資源作業。對于加油作業，每一停機區能夠同時加油的艦載機數量受該區加油站數量的限制；對于掛彈作業，受甲板配置的掛彈小組數約束；對于轉運作業，除了受轉運小組數量約束外，還受空間路徑約束；機務保障受機務保障小組數量約束，因機務作業可與加油掛彈并行作業，此處忽略該約束；慣導對準、暖機等作業受甲板可用暖機位數量的約束；滑行作業可視為不需甲板資源作業類型；起飛作業受起飛站位數量的約束，對于庫茲涅佐夫航母，每一時刻只能起飛1 架艦載機。

1.2 艦載機甲板作業調度的數學模型

模型中以一波次艦載機全部著艦滑行至臨時停機位為甲板航空保障作業調度起始點，不考慮再次出動機務檢修工作所需資源和用時。相關參數定義如下：艦載機 i ∈{1,···I} ， I為當前要需進行再次出動準備的艦載機架數；作業j ∈V，對于每一架艦載機，其甲板作業集，Ji為第i架艦載機需要執行的保障作業數量； Vnr， Vrs和 Vra分別代表非資源需求、特定資源、不定資源作業集。每一任務j 也屬于一個任務類型集 Ej，如果是非資源需求任務它等于j，并且包括所有需要同類資源的作業。注意到僅一種特定資源型任務存在于 Vi中，即起飛。 Vs表示由于安全原因不能同時執行的作業集，如對同一架飛機的加油和掛彈作業； Tij是艦載機 i 完成作業工序 j的時間，對于任一飛機的任一作業，因人員作業效率、加油量、掛彈種類及站位分布的不同，其作業時間不完全相同，但可根據統計任務持續時間的均值和3σ 之和作為該時間值，這種取值方法可以提高調度計劃的魯棒性； stij、edij分 別表示第 i 架艦載機第 j項作業的開始時間和結束時間； k ∈{1,···,K} 為調度時間序列； yijk∈{0,1}，當k = stij時 yijk= 1， 表 示 k 時 刻 第 i 架 艦 載 機 第 j項 作 業 開始； Ci為艦載機完成最后一道作業（起飛）的時間；每一飛機的順序作業型任務用帶權圖 Gi=(Vi,Ai)表示， 其中dmini是使得任務ni開始的時間間隙， Sni與任務 mi的開始時間相關，Smi滿足不等式為本波次再次出動準備時間； Njk是在某一時刻 k，執行作業j的可用甲板資源數量。

調度模型的目標函數取為最小化本波次艦載機的再次出動準備時間：

約束條件為：

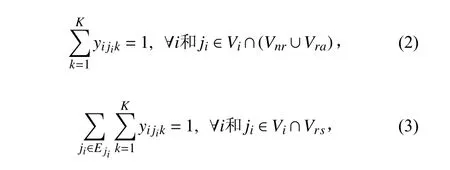
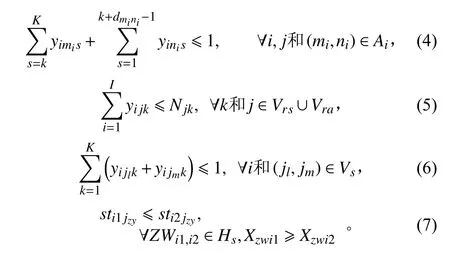
式（2）和式（3）聯合確保每一作業必須只被每一架飛機啟動一次，帶有僅單一資源的特定性任務需要額外執行要求的作業通過式（ 3） 強調。 不等式（4）確保作業期間的時序優先級條件，該不等式主要針對作業集 TS2。不等式（5）確保僅有有限數量的甲板資源被用于完成不定資源約束型作業，不等式（6）確保對于每一架飛機沒有2 個可以導致安全問題的作業同時進行，不等式（7）表示調運可行路徑約束通，其中 ZWi1表 示艦載機在甲板的停機站位， Hs表示艦艏區域站位集合；Xzwp表 示站位的 x坐 標， jzy表示轉運作業.

2 求解算法

若將待保障的艦載機視為工件，將保障資源視為加工機器，則艦載機循環出動的再次出動準備作業調度模型可視為具有工序順序不定、加工時間不確定的柔性車間作業調度問題，該問題屬于一類NP-難解問題，時間復雜度為因其解空間搜索量巨大，很難獲得精確的全局最優解。禁忌搜索已經被證明是解決該問題的較好算法，但基本禁忌搜索算法容易陷入局部極小，且初始解選取不同，最終得到的優化解的質量也存在差異，為解決該問題，本文采用迭代搜索，在算法中加入簡單的攝動策略，來幫助搜索跳出局部最優[8]。

2.1 算法總體框架

迭代禁忌搜索算法從某一局部極小值開始，重復地使用攝動策略使之逃離該局部極小值，并基于禁忌搜索算法去尋找另一局部極小，直到滿足停止條件。解的接受標準決定新的局部極小值是否被接受，還是繼續從一些以前訪問過的解繼續搜索。迭代禁忌搜索算法的總體框架如下：

步驟1function ITS（），

步驟2基于啟發式規則的初始解→s，

步驟3s←tabuSearch（s），

步驟4for ii = 1，…，maxIT do，

步驟5s′←perturb（s），(s′,i)

步驟6s←tabuSearch ，(ii/maxIT)2s?

步驟7以概率1- 接受：s← ，

步驟8end for，

步驟9返回搜索中發現的最優解 s?，

步驟10end function。

在該算法中，在第 ii次迭代結束時，新解以概率1?(ii/maxIT)2被接受。否則搜索繼續從當前的 s?開始，該值在搜索中被更新，并最終返回。接受標準被選擇在開始時分散搜索，而在最優解附近強化搜索。

2.2 基于啟發式規則的初始解生成

初始解的生成規則基于優先級索引策略、先到先服務和艦首區艦載機優先原則生成，具體規則如下：

1）對于掛彈、轉運作業類受限保障資源，優先分配給甲板首區停機位上待保障的艦載機；

2）對于加油作業，按照區域，首先進入該區域停機位的艦載機優先接受加油服務；

3）對于轉運作業，每一區域需要轉運的艦載機，按照后進先出的順序依次轉運；

4）在滿足相關約束條件的前提下，盡量避免長時間占用著艦跑道；

5）在甲板范圍內，盡可能保持各類保障資源的負擔均勻。

2.3 約束條件的處理

艦載機再次出動作業調度問題的約束條件比起一般的車間作業調度問題更為復雜，主要體現在 TS1作業集中的任務無固定作業順序，調運作業存在某些空間約束等。在實施搜索過程中，不判別解的可行性，而是對違反約束的解的工序之間插入時間間隙作為懲罰。以掛彈作業為例，具體算法如下：

步驟1function C aldt （）；

步驟2記錄沒架飛機第j 到作業工序為掛彈作業的飛機數為tgd，自增；

步驟3取當前艦載機作業工序j 的上一工序結束時間→T empJ；

步驟4若當前為所有飛機的第一道作業工序，且tdg ≤NGD（ 掛彈資源約束），則 d t = 0 ， 否則 d t = tgdd，tgdd為 d 區域的預計掛彈作業時間；

步驟5當前已安排掛彈作業的飛機數量 n gdTask ，并將其預計結束時間按從小到大排序；

步驟6若當前非第一道作業工序，且n gdTask ＜NGD，則 dt = 0 ， 否 則dt = max{tmpTgd(ngdTask ?NGD+1)}?tempJ,0。

2.4 領域構造策略

領域結構是對初始解進行一次移動操作而獲得另一個解的機制。在禁忌搜索算法中，領域結構直接影響禁忌搜索算法的搜索效率[9-11]。因艦載機再次出動甲板作業中，對于每架飛機集T S2中的作業優先順序固定，保障作業時間主要受各架機 TS1集中3 個作業工序安排順序的影響。為了兼顧搜索時間和解的質量，本算法中采用2 種領域，第1 種結構在啟發式初始解的基礎上，依次對每架飛機 TS1的作業順序進行交換和插入移動（3 個工序共可進行5 次移動）；第2 種領域結構是在攝動函數中對待保障的所有 I 架艦載機 T S1集的第 j道作業工序進行約束條件檢驗，并按最小違背原則進行移動。

3 算例仿真

以庫茲涅佐夫航母為實例，對8 機雙周期連續出動模式下的艦載機再次出動保障進行調度仿真。甲板初始停機數設為16 架，假設連續出動過程中所有艦載機均無故障，艦載機各作業工序的時間取值如下：加油時間tjy= 18 min ； 掛彈時間取為[ tdgstgdztgdzwtgdyw]=min ；轉運時間 tzy= 7 min；慣導對準時間 tdz= 8 min ；暖機時間 tnj= 8 min；滑行和起飛時間分別為 thx= 1 min 和 tqf= 1 min。 掛彈小組數NGD= 4； 轉運組數 NZY= 3。算法基于MATLAB R2014a實現，計算機配置為2.4 GHz 主頻，8 G 內存，Win7系統。文中算法（I-TB) 與模擬退火（SA）算法、普通禁忌搜索（TB）算法以及全局搜索算法的計算結果如表1 所示。表中耗時是指獲得優化解的用時，時間差別主要因算法收斂速度引起。文中算法解的收斂曲線如圖2 所示，8 機出動模式下的作業調度甘特圖如圖3 所示。圖中矩形內數字表示飛機號×100+作業序號，作業序號1～7 依次表示加油、掛彈、轉運、慣導對準、暖機、滑行和起飛。

從仿真結果可以看出， I-TB 算法、 SA 算法、TB 算法較全局搜索算法的搜索效率均有非常顯著的提高，其中I-TB 算法搜索時間最短；在解的質量方面，全局搜索算法可獲得全局最優解，其他3 種算法均無法保證獲得全局最優解，但I-TB 算法與TB 和SA 相比解的質量更高。從調度算法輸出的甘特圖上看，算法結果能夠獲得調度專家的認可。

表 1 算法性能對比Tab.1 Performance evaluation of algorithms

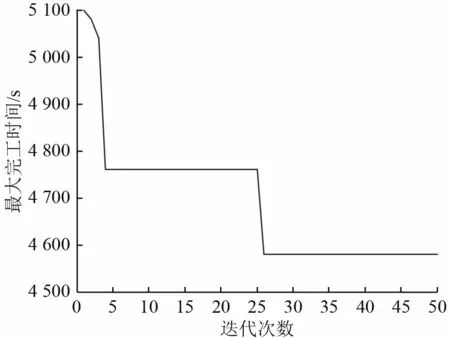
圖 2 I-TB 算法收斂曲線Fig.2 Convergence curve of I-TB algorithm

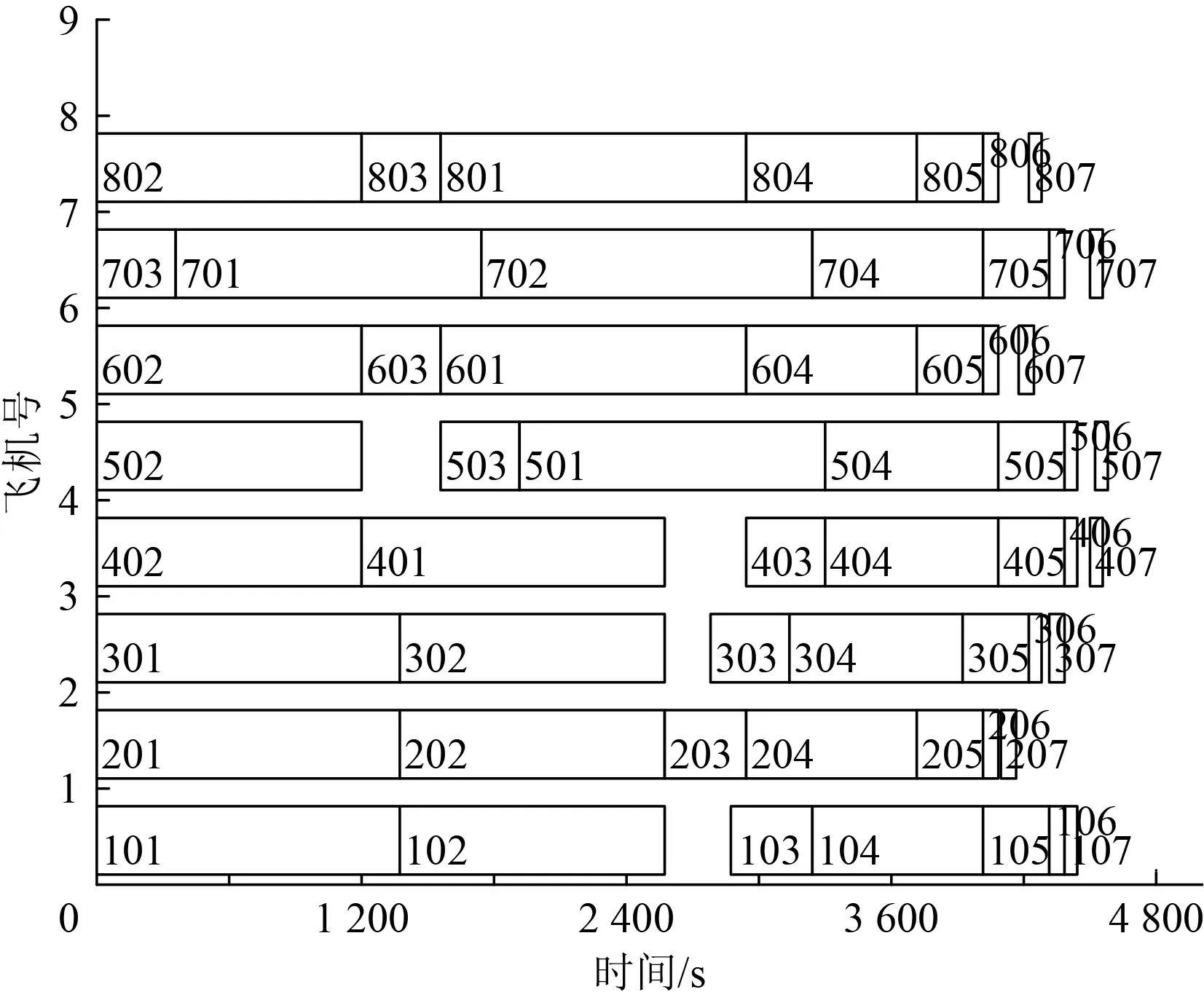
圖 3 8 機再次出動準備調度時序圖Fig.3 Turnaround operations scheduling diagram for 8 carrier aircrafts

4 結 語

本文針對雙周期連續出動模式下的艦載機艦面保障作業調度問題，通過分析作業流程和資源約束條件，以優化批次飛機最短再次出動準備時間為目標，建立了優化計算模型。在此基礎上，采用迭代禁忌搜索算法框架設計了一種基于啟發式初始解的快速求解算法，并給搜素過程中的約束條件處理測量和領域構造策略。通過以庫茲涅佐夫航母為背景的仿真計算驗證了算法的有效性，且算法獲得的調度結果能夠被甲板調度專家接受。