基于消費者心理學的尖峰電價優化研究

朱鋁芬，周 珣，陳美玲，張 云

（南京工業大學浦江學院，江蘇 南京 211100）

0 引 言

隨著我國經濟的飛速發展，電力需求持續增長，僅依靠擴大投資規模、增加裝機容量來滿足短暫的高峰用電，必然導致發電資源的極大浪費，也會加重電力企業的負擔。融入消費者心理學，利用價格信號或激勵作用，使用戶的用電方式發生改變，從而保障電網的穩定[1-7]。尖峰電價具有削峰填谷、平緩系統負荷的作用，國內外對此作出了很多研究。文獻[8]搭建了綜合考慮電力用戶、風電場及供電公司利益的多目標變時段尖峰電價決策模型，通過風速的蒙特卡羅模擬，結合遺傳算法對模型進行求解。本文融入消費者心理學，以實現削峰填谷和使用戶滿意度最大化為目的建立尖峰電價模型，并結合改進粒子群算法優化模型。

1 基于消費者心理學的用戶響應尖峰電價行為分析

文章融入消費者心理學，利用價格信號改變用戶用電方式，從而實現削峰填谷。以居民負荷為研究對象進行負荷特性分析，并在此基礎上融入消費者心理學進行居民用戶對電價的靈敏度分析，獲得負荷轉移率曲線[8]，如圖1所示。

圖1 負荷轉移率

圖1表明，銷售電價對居民用戶的刺激有一個最小可覺差。當電價小于最小可覺差時，居民用戶基本上無反應；當電價大于一個上限值時，居民用戶不再有更多的可轉移負荷，響應趨近飽和。負荷轉移率為[9]：

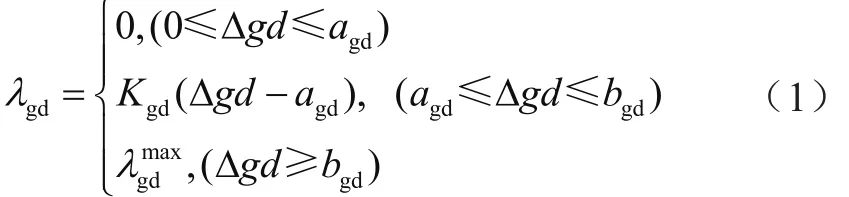
式中：d、g分別為低電價、高電價，Δgd=g-d；agd、bgd分別為用戶對電價差在死區及線性區的上限值；Kgd為斜率。

基于消費者心理學的尖峰電價費率體系包含尖峰日和非尖峰日，共有6類負荷轉移率，即尖-谷轉移率λcg、尖-平轉移率λcp、尖-峰轉移率λcf、峰-谷轉移率λfg、峰-平轉移率λfp、平-谷轉移率λpg。

2 建立基于消費者心理學的負荷響應模型

假設某地區所有簽訂了尖峰電價合同的用戶，其負荷響應模型可用一組基于消費者心理學理論的折線表示，則可建立單一電價轉變為尖峰電價后尖峰日的負荷響應模型：

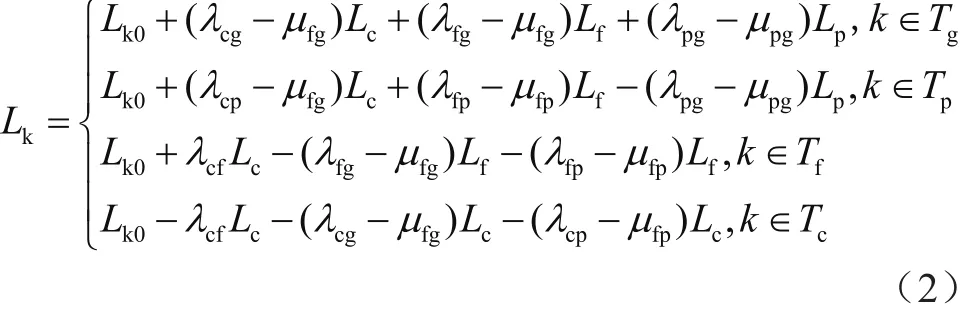
式中：Tc、Tf、Tp、Tg分別為尖峰時段、峰時段、平時段、谷時段；k為其中的任一時段；Lk0、Lk分別為CPP實施前、后k時段的負荷；Lc、Lf、Lp、Lg分別為CPP實施前尖、峰、平、谷時段的負荷值；μfg、μfp、μpg分別為實行分時電價時的峰-谷、峰-平、平-谷的轉移率。

非尖峰日的負荷響應模型與尖峰日的負荷響應模型類似，不重復闡述。

3 建立基于消費者心理學的尖峰電價優化模型

本文以尖峰日尖峰時段電價Pc、非尖峰日電價折扣率r為變量，實現月負荷的最大峰荷最小化、月負荷的峰谷差最小化及用戶滿意度最大化，建立多目標的規劃模型[10]：

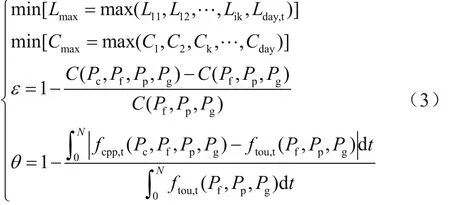
式中：Lday,t為執行CPP后第day天t時刻的負荷，Lmax為執行CPP后該月的最大負荷；Cday為執行CPP后第day天的峰谷差，Cmax為執行CPP后該月的最大峰谷差；ε為用戶電費支出滿意度，C(Pc,Pf,Pg)為實行峰谷分時電價時用戶的電費支出，C(Pc,Pf,Pp,Pg)為實行尖峰電價后用戶的電費支出；θ為用戶用電方式滿意度，N為計算時間段數為實行尖峰電價的用戶各時段用電量變化值。

利用設定權值法，將多目標函數轉化為單目標規劃：

式中，Lmax0為執行CPP前該月的最高負荷，Cmax0為執行CPP前該月的最大峰谷差，ω1、ω2分別代表用戶對系統削峰填谷的貢獻以及自身滿意度的權重。

尖峰電價模型為非線性混合規劃模型，目標函數具有一定的復雜性，通過改進粒子群算法優化模型參數即Pc、r，相對于傳統粒子群算法引入基于精英個體適應值方差的混沌搜索策略和自適應激活機制，有效提高了其全局搜索能力，緩解了“早熟現象”。

4 算例驗證

以某市2017年8月份的居民負荷數據為基礎進行算例驗證。算例中，設置ω1=0.6，ω2=0.4，采用改進粒子群算法求解。結果為Pc=1.35元/kW·h，r=0.95，尖峰電價上浮了200%。執行前后最高負荷減少了212 MW，下降了11.5%；最大峰谷減少了47 MW，下降了3.82%；電網公司的月售電收入增加了173萬元。圖2為尖峰電價實施前后的負荷曲線。

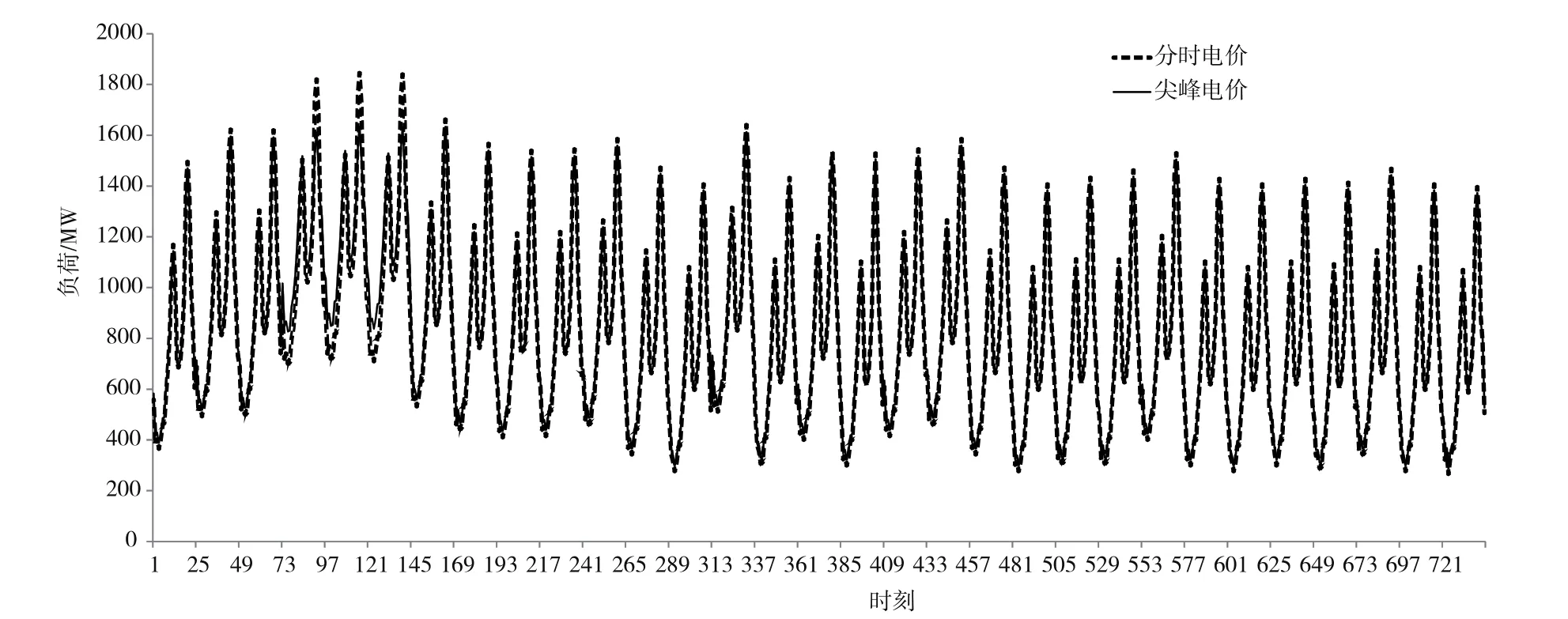
圖2 尖峰電價實施前后負荷曲線比較

截取某尖峰日執行尖峰電價前后的負荷數據作曲線對比，如圖3所示。

圖3 某尖峰日尖峰電價實施前后負荷曲線比較

5 結 論

本文融入消費者心理學對尖峰電價模型進行研究，利用改進粒子群算法優化模型，并通過算例驗證其可行性，為尖峰電價的實施提供了科學的理論依據。然而，本文采用的負荷響應模型過于粗糙，用戶的響應情況實際處于動態變化之中，與負荷類型、季節等多種因素相關，應采用幾條不同的作用機理折線表示，并隨著時間的發展不斷修正，這將是下一步的研究內容。