PI參數(shù)對(duì)RSC控制及DFIG轉(zhuǎn)子電流特性的影響
王鵬飛,趙彥琦
PI參數(shù)對(duì)RSC控制及DFIG轉(zhuǎn)子電流特性的影響
王鵬飛,趙彥琦
(武漢船用電力推進(jìn)裝置研究所,武漢 430064)
轉(zhuǎn)子變流器(RSC)內(nèi)環(huán)PI參數(shù)對(duì)其控制穩(wěn)定性及轉(zhuǎn)子電流暫態(tài)特性影響較大。基于DFIG數(shù)學(xué)模型,推導(dǎo)出轉(zhuǎn)子電流在擾動(dòng)狀態(tài)下的解析表達(dá)式。對(duì)開環(huán)傳遞函數(shù)簡(jiǎn)化,分析不同PI參數(shù)對(duì)控制系統(tǒng)穩(wěn)定性和帶寬頻率的影響。動(dòng)態(tài)仿真結(jié)果表明:在滿足系統(tǒng)穩(wěn)定性和帶寬頻率的要求下,較大的PI參數(shù)能抑制故障下的轉(zhuǎn)子電流峰值,有利于電壓輕度跌落下DFIG故障穿越。
雙饋風(fēng)電機(jī)組 轉(zhuǎn)子變流器 PI參數(shù) 穩(wěn)定性分析
0 引言
雙饋風(fēng)電機(jī)組(doubly-fed induction generator, DFIG)轉(zhuǎn)子側(cè)變流器(rotor side converter, RSC)通過PI環(huán)對(duì)轉(zhuǎn)子電壓進(jìn)行控制,從而實(shí)現(xiàn)對(duì)整個(gè)機(jī)組的運(yùn)行控制[1,2],因此PI參數(shù)將直接影響RSC內(nèi)環(huán)控制性能及轉(zhuǎn)子電流暫態(tài)特性。RSC的PI參數(shù)取值是根據(jù)系統(tǒng)要求的控制性能綜合確定的,其本質(zhì)為電壓型PWM整流器的電流內(nèi)環(huán)參數(shù)設(shè)計(jì),文獻(xiàn)[3]對(duì)此有詳細(xì)介紹。文獻(xiàn)[4]據(jù)此設(shè)計(jì)出典型I型和II型系統(tǒng)RSC的PI參數(shù)。文獻(xiàn)[5]在分析了PI參數(shù)對(duì)故障后定子電流的直流衰減分量的影響,但并未對(duì)控制穩(wěn)定性進(jìn)行分析。深入分析PI參數(shù)對(duì)其轉(zhuǎn)子控制的穩(wěn)定性和電流暫態(tài)特性的影響,現(xiàn)有文獻(xiàn)較少提及。
本文根據(jù)DFIG數(shù)學(xué)模型,推導(dǎo)出轉(zhuǎn)子電流解析表達(dá)式。根據(jù)轉(zhuǎn)子電流開環(huán)傳遞函數(shù),對(duì)其進(jìn)行降階化簡(jiǎn),確定比例與積分參數(shù)的關(guān)系。分析了PI參數(shù)對(duì)控制系統(tǒng)穩(wěn)定性和控制帶寬的影響,近似確定PI參數(shù)的取值范圍;討論了不同PI參數(shù)對(duì)轉(zhuǎn)子電流的暫態(tài)特性的影響。動(dòng)態(tài)仿真結(jié)果驗(yàn)證了上述理論推導(dǎo)的正確性。
1 計(jì)算RSC控制轉(zhuǎn)子電流解析表達(dá)式
雙饋感應(yīng)電機(jī)各物理量正方向采用電動(dòng)機(jī)慣例,在dq旋轉(zhuǎn)坐標(biāo)系下,其定、轉(zhuǎn)子電壓和磁鏈方程分別為:
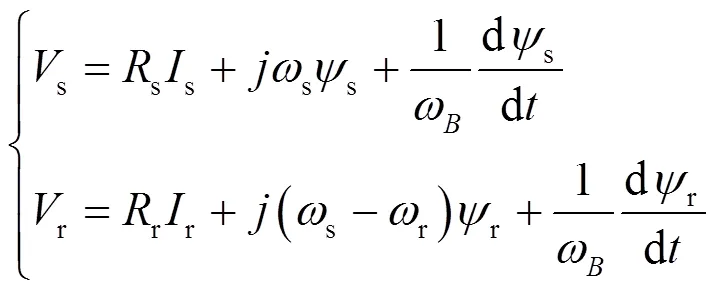
式中,s、r、s、r、s、r分別表示為定、轉(zhuǎn)子電壓、電流、磁鏈;s、r分別表示定、轉(zhuǎn)子電阻;s、r、m分別表示為定、轉(zhuǎn)子側(cè)自感和勵(lì)磁電感;s、r、B分別表示為定、轉(zhuǎn)子及同步角速度;除、B外,上述變量均為標(biāo)幺值。
轉(zhuǎn)子變流器的內(nèi)環(huán)控制方程可表示為:

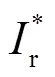
設(shè)s不變,為計(jì)算方便,將式(1)~(3)寫成增量形式后進(jìn)行拉普拉斯變換,得到轉(zhuǎn)子電流與其參考值和定子電壓的傳遞函數(shù)表達(dá)式:
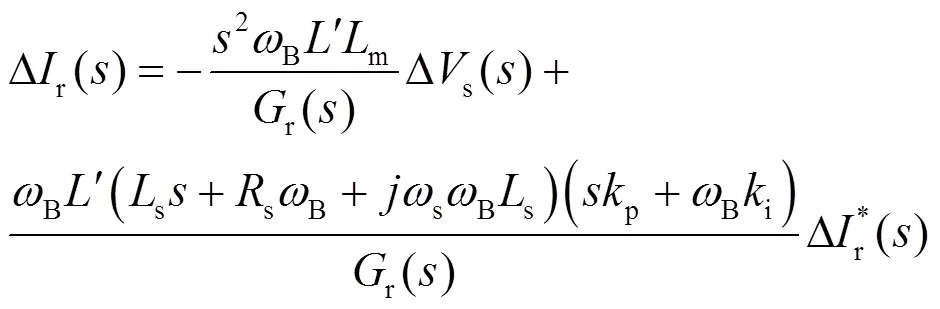
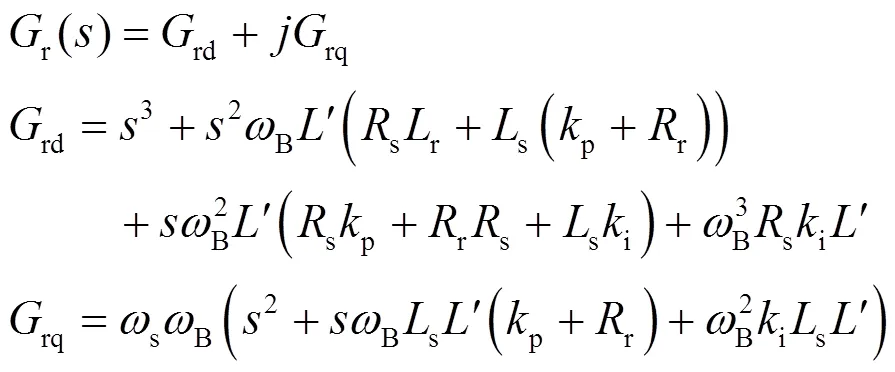
式中,'=1/(rs-m2)為中間變量,r(s)為傳遞函數(shù)分母多項(xiàng)式,rd、rq分別為其實(shí)部和虛部。
由式(4)可知,轉(zhuǎn)子電流與其參考值和定子電壓有關(guān)。當(dāng)外網(wǎng)故障時(shí),會(huì)引起定子電壓變化;而參考值由功率外環(huán)控制,一般是由風(fēng)速、DFIG工況變化,引起定子功率參考值改變,最終導(dǎo)致轉(zhuǎn)子電流參考值變化。本文僅考慮內(nèi)環(huán)PI參數(shù)對(duì)轉(zhuǎn)子電流控制追蹤能力和對(duì)定子電壓的抗干擾能力的影響,因而忽略功率外環(huán)控制。當(dāng)定子電壓和轉(zhuǎn)子電流參考值階躍變化,可得到轉(zhuǎn)子電流解析表達(dá)式,從而直接分析PI參數(shù)對(duì)轉(zhuǎn)子電流影響。
基于定子電壓d軸定向,設(shè)定子電壓由sd變?yōu)閟d,轉(zhuǎn)子電流參考值的增量為Δr,它們?cè)隽康睦阶儞Q分別為:
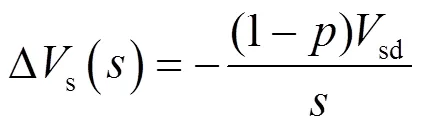
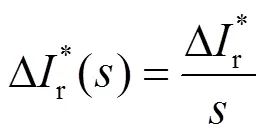
將式(6)、(7)代入(4)中,再經(jīng)過反拉普拉斯變換,可得到轉(zhuǎn)子電流的增量解析表達(dá)式:
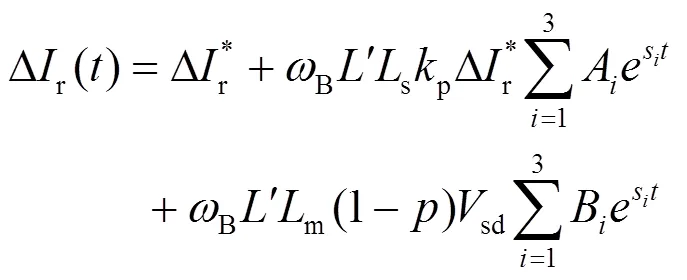
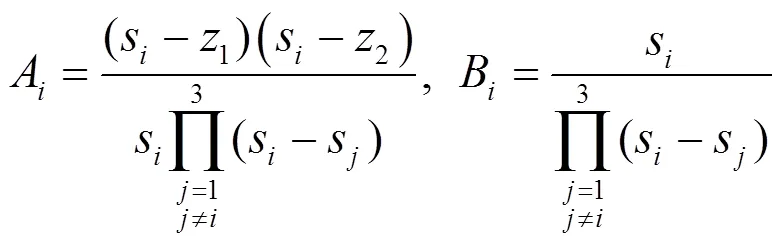
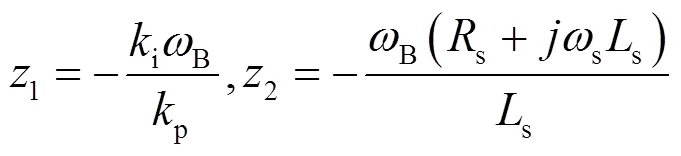
式中:s(=1,2,3)為多項(xiàng)式r(s)的三個(gè)解;A,B,1,2分別見式(9,10)。
由式(8~10)可知,定子電壓、轉(zhuǎn)子電流參考值階躍變化時(shí),轉(zhuǎn)子電流將會(huì)產(chǎn)生三個(gè)暫態(tài)分量,這三個(gè)分量的幅值、角頻率、衰減時(shí)間常數(shù)均與PI參數(shù)和感應(yīng)電機(jī)的參數(shù)有關(guān),而與風(fēng)電機(jī)組的初始運(yùn)行狀態(tài)無關(guān)。
2 PI參數(shù)的整定及其穩(wěn)定性分析
2.1 PI參數(shù)關(guān)系整定
由式(8)可知,轉(zhuǎn)子電流暫態(tài)分量與PI參數(shù)取值關(guān)系密切,因此有必要根據(jù)控制環(huán)的比例系數(shù)與積分系數(shù)間關(guān)系,分析其參數(shù)對(duì)轉(zhuǎn)子電流暫態(tài)的影響,同時(shí)亦可為PI參數(shù)選擇提供依據(jù)。
PI參數(shù)設(shè)計(jì)一般根據(jù)開環(huán)傳遞函數(shù),利用工程設(shè)計(jì)方法得到。因此將式(4)進(jìn)行dq軸分解。可以得到:
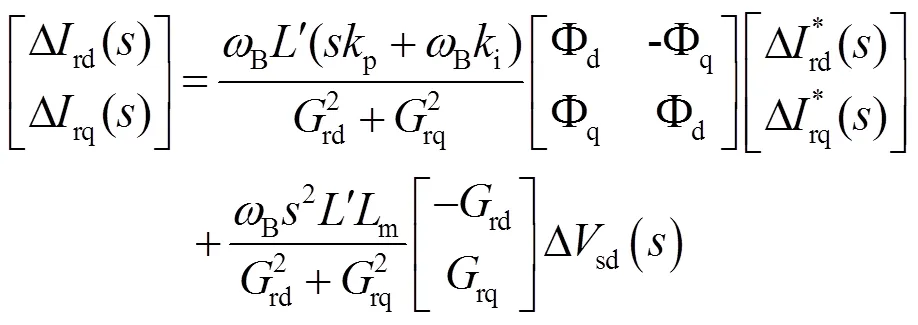
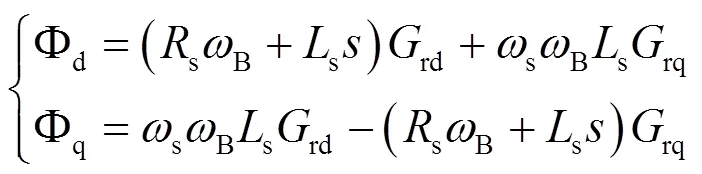
式中,d、q為中間多項(xiàng)式。
由式(12)可知,Δsd,Δrq*均為rd的擾動(dòng)項(xiàng),且d、q軸閉環(huán)傳遞函數(shù)相同,故僅以d軸為例進(jìn)行分析,根據(jù)閉環(huán)傳遞函數(shù),可得到d軸開環(huán)傳遞函數(shù)d為:
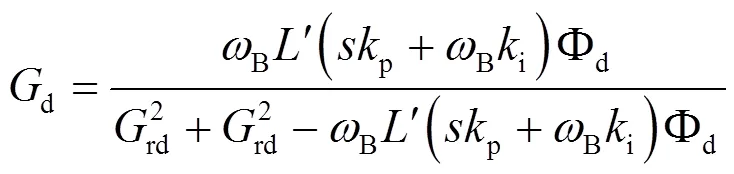
將式(13)分子分母多項(xiàng)式進(jìn)行因式分解,約去公因式,可以近似得:
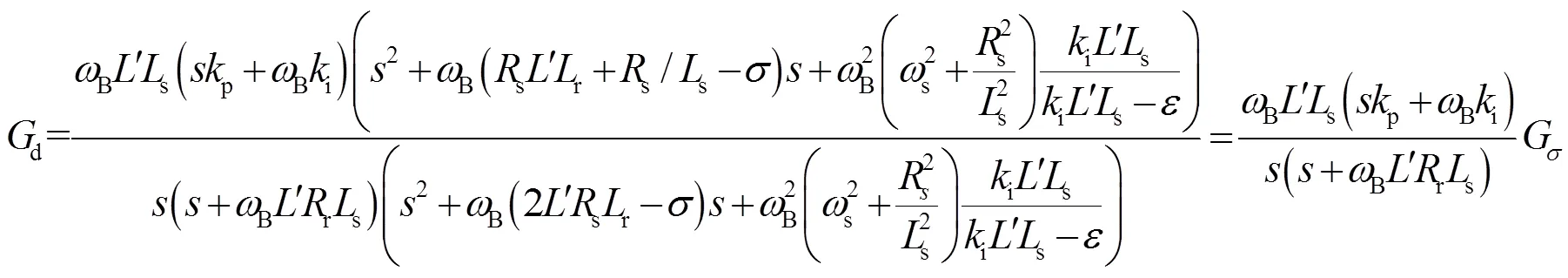
式中,、是p、i均有關(guān)的偏移量,其詳細(xì)表達(dá)式見文獻(xiàn)[5],而σ項(xiàng)見式(15)。
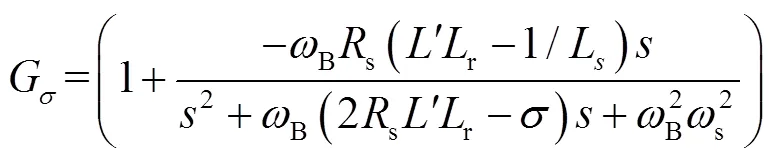
在RSC的PI參數(shù)設(shè)計(jì)時(shí),一般希望轉(zhuǎn)子電流能快速、平穩(wěn)地追蹤電流參考值,當(dāng)發(fā)生擾動(dòng)時(shí),轉(zhuǎn)子電流超調(diào)量盡量小,衰減速度足夠快。而上述開環(huán)傳遞函數(shù)含有σ項(xiàng),其類似于諧振頻率為B,的陷波器,當(dāng)輸入信號(hào)的角頻率偏離B時(shí),σ=1。因此,利用工程PI參數(shù)設(shè)計(jì)方法,將上述簡(jiǎn)化開環(huán)傳遞函數(shù)零極點(diǎn)對(duì)消,可以得到PI參數(shù)關(guān)系和閉環(huán)系統(tǒng)截止頻率c:
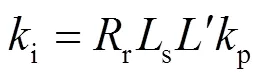
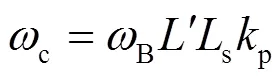
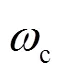
上述PI參數(shù)的關(guān)系是根據(jù)忽略σ項(xiàng)后的簡(jiǎn)化開環(huán)傳遞函數(shù)得到的,其實(shí)際性能是與理想的性能之間的誤差仍有待檢驗(yàn),因此需要對(duì)其進(jìn)行穩(wěn)定性分析。
2.2 不同PI參數(shù)對(duì)其穩(wěn)定性的影響
圖1給出了不同取值p下,精確與簡(jiǎn)化的開環(huán)傳遞函數(shù)Bode圖,以p=0.2為例進(jìn)行分析。當(dāng)頻率遠(yuǎn)離B時(shí),精確和簡(jiǎn)化的開環(huán)對(duì)數(shù)幅頻、相頻特性曲線基本重合,且幅頻特性曲線斜率為-20 dB/dec,相角在90°附近;而頻率在B附近時(shí),精確開環(huán)對(duì)數(shù)幅頻特性曲線向下凹陷,如圖中CAD所示,相頻特性曲線先凹后凸,如FEGH所示。且p越大,峰值點(diǎn)偏離越遠(yuǎn)。這驗(yàn)證了在該段頻率下σ=1,而在B附近產(chǎn)生負(fù)的諧振峰,將不利于系統(tǒng)的穩(wěn)定。
控制系統(tǒng)中一般可以用相角裕度表征系統(tǒng)的穩(wěn)態(tài)性能,開環(huán)截止頻率(或閉環(huán)帶寬頻率)來表征系統(tǒng)的瞬態(tài)性能。σ的陷波器特性將對(duì)系統(tǒng)的相角裕度和開環(huán)截止頻率產(chǎn)生較大影響。當(dāng)p較小時(shí),相角裕度始終在90°附近,隨著p增大,幅頻特性曲線向上移動(dòng),當(dāng)圖中CA段與0 dB相交時(shí),其相角裕度逐漸降低,而截止頻率則在B附近。隨著幅頻特性曲線B附近的最低點(diǎn)A點(diǎn)提高到0 dB以上,截止頻率將會(huì)從B跳變到與簡(jiǎn)化傳遞函數(shù)的截止頻率相同,如圖中K點(diǎn)所示。
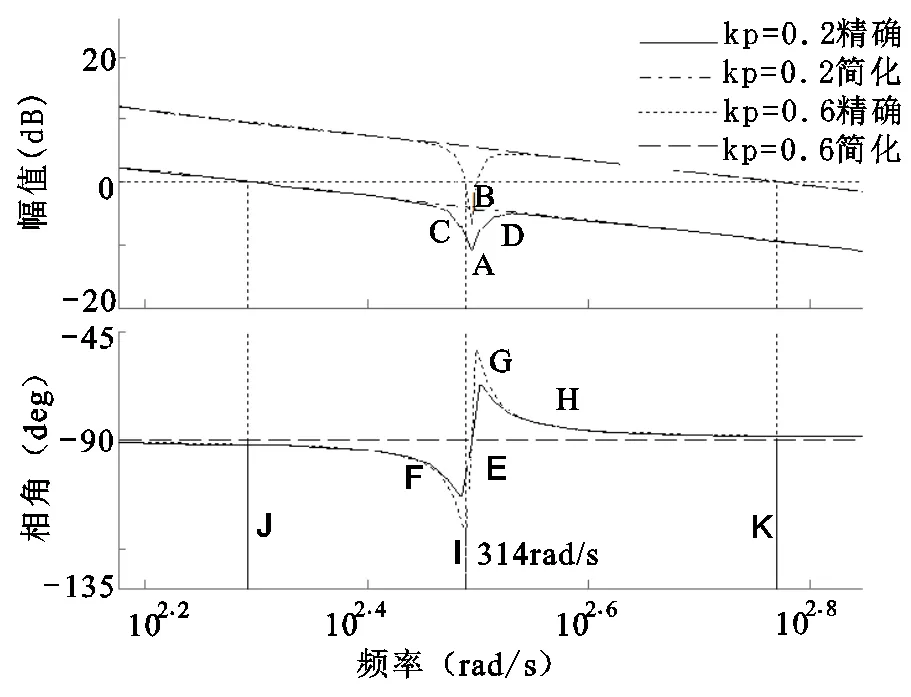
圖1 不同PI參數(shù)的開環(huán)傳遞函數(shù)博德圖
綜上所述,隨著p的增大,系統(tǒng)的相角裕度在減小,由式(17)可知,系統(tǒng)的帶寬頻率與p成正比,p大的系統(tǒng)帶寬大,動(dòng)態(tài)響應(yīng)快,跟隨性能好,但其抗干擾能力減弱,擾動(dòng)恢復(fù)時(shí)間將會(huì)延長(zhǎng)。
3 算例分析
3.1 解析表達(dá)式的驗(yàn)證
在MATLAB上建立DFIG仿真模型進(jìn)行驗(yàn)證。假設(shè)在t=0.1 s時(shí),電網(wǎng)發(fā)生三相故障,持續(xù)時(shí)間0.625 s,忽略定子電壓的波動(dòng),假定定子電壓跌落系數(shù)p=0.7;故障前DFIG額定功率運(yùn)行,無功功率為0;故障后保持轉(zhuǎn)子電流參考值保持不變,仿真歩長(zhǎng)取0.0001 s;PI參數(shù)為p=0.15,i=0.0042;
由圖2可知,仿真與計(jì)算結(jié)果基本重合,從而驗(yàn)證了文中所得的轉(zhuǎn)子電流的解析表達(dá)式的正確性。同時(shí),轉(zhuǎn)子電流波動(dòng)的強(qiáng)弱體現(xiàn)了控制系統(tǒng)抗定子電壓擾動(dòng)的能力。

圖2 轉(zhuǎn)子電流解析表達(dá)與仿真對(duì)比圖
3.2 PI參數(shù)對(duì)轉(zhuǎn)子電流動(dòng)態(tài)性能的影響
分析不同的PI參數(shù)對(duì)轉(zhuǎn)子電流暫態(tài)特性的影響,首先需確定滿足控制系統(tǒng)性能的PI參數(shù)的范圍。工程中一般要求相角裕度不低于45°[6],取變流器開關(guān)頻率s=1.5 kHz[7],可確定PI參數(shù)的上限。當(dāng)p變化時(shí),其帶寬頻率約為B,不妨假設(shè)系統(tǒng)設(shè)計(jì)要求帶寬頻率下限值為B,其中0<<1,可求解PI參數(shù)的下限。不妨取系數(shù)=0.5,可以得到控制系統(tǒng)的p范圍為0.15~0.48,其相角裕度為57~89°。下面在此范圍內(nèi),討論P(yáng)I參數(shù)對(duì)轉(zhuǎn)子電流動(dòng)態(tài)性能的影響。
為了觀察轉(zhuǎn)子電流追蹤性能和抗干擾性能,設(shè)在=0.1 s時(shí),rq*階躍變化,其變化量為-0.2 pu,rd*參考值不變,轉(zhuǎn)子電流參考值變化前DFIG額定功率運(yùn)行,無功功率為0。此情況下,可觀察q軸電流追蹤能力和對(duì)d軸電流抗干擾能力;在=0.6 s時(shí),定子電壓跌落到原電壓的0.7倍,持續(xù)0.8 s,可觀察定子電壓跌落擾動(dòng)對(duì)轉(zhuǎn)子dq軸電流影響。當(dāng)取p分別取0.15和0.3時(shí),轉(zhuǎn)子動(dòng)態(tài)響應(yīng)如圖3所示。
由圖3(a)可知,p參數(shù)取較大時(shí),轉(zhuǎn)子電流追蹤速度快,穩(wěn)態(tài)恢復(fù)時(shí)間延長(zhǎng);圖3(b)可知,轉(zhuǎn)子q軸電流參考值變化對(duì)d軸電流的擾動(dòng)量較小,可以忽略不計(jì),但p大的,擾動(dòng)后的電流峰值較小,衰減時(shí)間同樣會(huì)延長(zhǎng);而對(duì)于電壓擾動(dòng),由圖3(a)、3(b)可知,在前兩個(gè)周波內(nèi),轉(zhuǎn)子d、q軸峰值電流均較小,其衰減速度同樣較慢。由圖3(c)可知,p較大時(shí),轉(zhuǎn)子電壓升高,因此可以認(rèn)為,增大PI參數(shù)是通過提高轉(zhuǎn)子電壓來抑制轉(zhuǎn)子電流的。同時(shí),由式(8)可知,由定子電壓跌落引起的轉(zhuǎn)子電流增量的峰值與電壓跌落程度成正比,因此,在滿足控制系統(tǒng)穩(wěn)定性和帶寬頻率以及轉(zhuǎn)子電壓幅值限制的條件下,p越大,轉(zhuǎn)子電流的峰值越小,越有利于DFIG的故障穿越,但不利于系統(tǒng)的快速恢復(fù)。
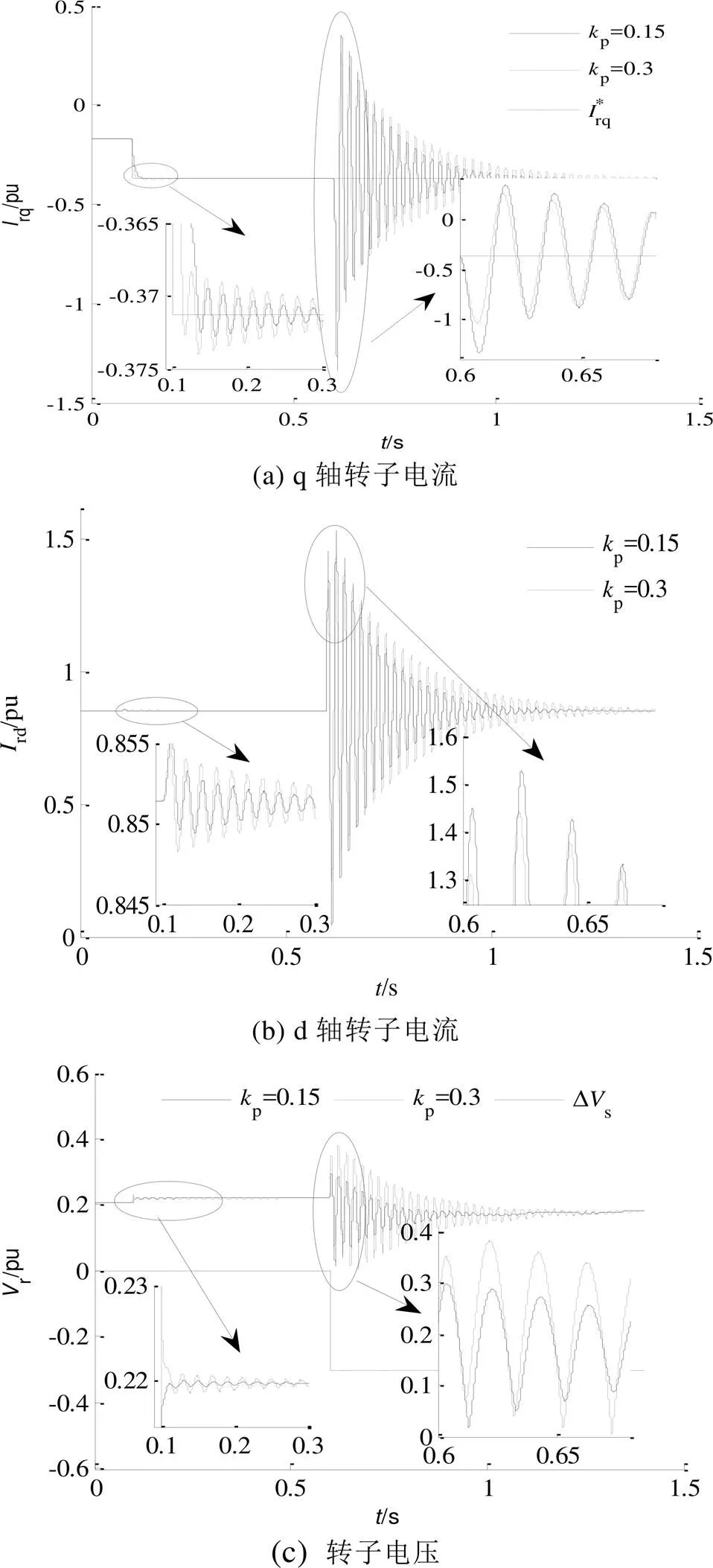
圖3 不同PI參數(shù)下轉(zhuǎn)子電流、電壓
4 結(jié)論
1)由于開環(huán)傳遞函數(shù)中類似于陷波器的存在,電流內(nèi)環(huán)控制系統(tǒng)的穩(wěn)定性于設(shè)計(jì)時(shí)相比,開環(huán)傳遞函數(shù)中有類似于陷波器項(xiàng)存在,當(dāng)輸入頻率在B附近時(shí),電流內(nèi)環(huán)控制系統(tǒng)的穩(wěn)定性將大幅降低。
2)PI參數(shù)的取值范圍可以根據(jù)RSC設(shè)計(jì)內(nèi)環(huán)頻率帶寬和變流器的開關(guān)頻率確定。
3)在滿足其穩(wěn)定性和帶寬頻率的要求下,p越大,轉(zhuǎn)子電流峰值越小,抗定子電壓擾動(dòng)的能力越強(qiáng),有利于DFIG的故障穿越,但其穩(wěn)定性逐漸降低,轉(zhuǎn)子電流內(nèi)環(huán)的追蹤速度變慢,衰減時(shí)間延長(zhǎng),轉(zhuǎn)子電壓峰值增大,因此需要折衷,合理選取PI參數(shù)。
[1] 周天保. 雙饋風(fēng)電機(jī)組電磁暫態(tài)解析及Crowbar拓?fù)溲芯縖D]. 合肥工業(yè)大學(xué), 2016.
[2] 張金華, 張保會(huì), 郝治國(guó),等. 故障后轉(zhuǎn)子側(cè)變流器不間斷控制下的雙饋風(fēng)機(jī)序網(wǎng)等值電路[J]. 電網(wǎng)技術(shù), 2017, 41(2):521-528.
[3] 張興, 張崇巍. PWM整流器及其控制[M]. 北京: 機(jī)械工業(yè)出版社, 2012.
[4] Kong X, Zhang Z, Yin X, et al. Study of Fault Current Characteristics of the DFIG Considering Dynamic Response of the RSC[J]. IEEE Transactions on Energy Conversion, 2014, 29(2):278-287.
[5] 王鵬飛. 雙饋風(fēng)電機(jī)組參與調(diào)頻及故障后有功支援研究[D]. 合肥工業(yè)大學(xué), 2018.
[6] 王孝武, 方敏, 葛鎖良. 自動(dòng)控制理論[M]. 北京: 機(jī)械工業(yè)出版社, 2012.
[7] 駱皓, 林明耀, 胡炫, 等. 基于開關(guān)頻率函數(shù)的雙饋發(fā)電機(jī)轉(zhuǎn)子勵(lì)磁I-PI雙電流環(huán)參數(shù)整定[J].電力自動(dòng)化設(shè)備, 2010, 30(4): 59-62.
Influence of PI Parameters on the RSC control and Rotor Current Characteristics of the DFIG
Wang Pengfei, Zhao Yanqi
(Wuhan Institute of Marine Electric Propulsion, Wuhan 430064, China)
(),
TM31 文獻(xiàn)標(biāo)示碼:A
1003-4862(2019)11-0048-04
2019-4-30
王鵬飛(1991-),男,碩士。研究方向: 電機(jī)與控制。E-mail: 840510875@qq.com

