基于動態數據反演的相滲曲線及應用效果

崔傳智 鄭文乾 李立峰 馮緒波 吳忠維

1.中國石油大學(華東)石油工程學院；2.中國石化江蘇油田分公司采油一廠

0 引言

油藏數值模擬研究中，通常采用基于巖心驅替測得的相對滲透率曲線進行計算，由于巖心所代表的儲層物性受局限［1-3］，且油藏物性在高含水期會發生變化，所以基于原始巖心驅替實驗獲得的相對滲透率不能完全表征實際的油水流動能力［4-7］。

在注水開發過程中，油藏儲層物性、開發方式等動態變化都會綜合反映在生產數據中，因此基于油藏動態數據反演的相對滲透率曲線能真實反映實際的油水流動能力。國內學者深入研究了水驅特征曲線和相對滲透率的關系：蔣明等［8］利用乙型水驅特征曲線推導出用于計算不同時刻含水飽和度和油水相對滲透率比值的關系式，再結合相對滲透率的指數關系式求解相滲曲線；閻靜華等［9］依據甲型水驅特征曲線直線段出現后的數據計算出系數值，再根據相對滲透率的指數函數計算出相對滲透率曲線；楊宇等［10］采用適用范圍很廣的張金慶水驅特征曲線對相對滲透率曲線進行了理論推導；王繼強等［11］應用二項式函數擬合特高含水期油水相對滲透率的比值與含水飽和度在半對數坐標上的關系，推導出了適用于特高含水期滲透率的計算方法。以上成果對于研究油水流動能力具有指導意義，但也存在一些不足，先計算不同含水飽和度對應的油水相對滲透率比值，再根據相對滲透率的指數關系式求解相滲曲線，需要進行多次回歸，并且在求不同含水飽和度對應的油水相對滲透率比值時需要基于一些經驗公式，導致公式的求解結果受人為因素影響，且這些公式未考慮油藏物性的變化。

在前人研究的基礎上，利用能綜合反映油藏儲層物性、開發方式等變化的動態生產數據，反演獲得了能夠反映真實油水流動能力的相對滲透率曲線。將基于動態數據反演的相滲曲線應用到實際油藏模型，通過對比含水率變化驗證了基于動態數據反演的相滲曲線更加真實準確地反映了實際油水能力。最后分析了基于動態數據反演的相滲曲線、巖心驅替獲得的常規相滲曲線對剩余油分布的影響，為水驅油藏后期開發與優化提供理論支持。

1 利用動態數據計算相滲曲線

1.1 利用動態數據計算相滲曲線的理論推導

水驅砂巖油藏的相對滲透率曲線一般可采用文獻［11-13］中的表達式

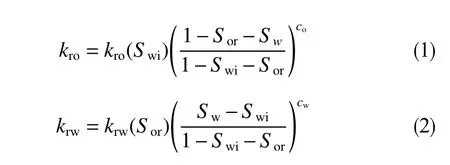
式中，kro、krw分別為油、水的相對滲透率；Swi為束縛水飽和度；kro(Swi)為束縛水下油的相對滲透率；krw(Sor)為殘余油飽和度下水的相對滲透率；Sor為殘余油飽和度；Sw為含水飽和度；co、cw為系數。

由式(1)、(2)可推導出

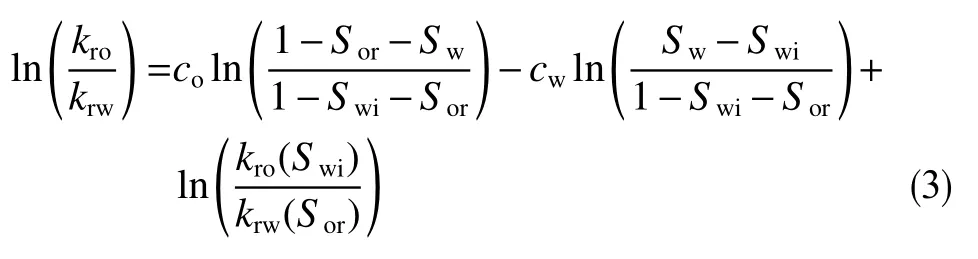
分流量方程關系式為

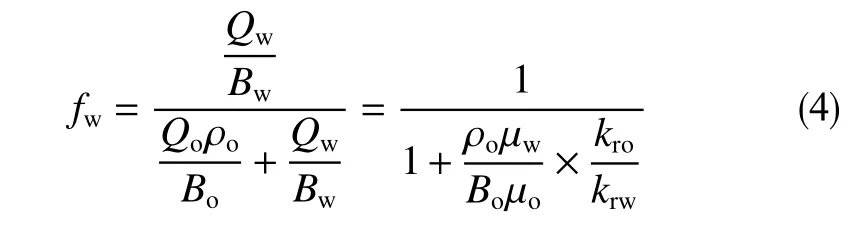
式中，fw為含水率；Qo、Qw分別為油、水的地下體積流量，m3/d；Bo為油的體積系數；Bw為水的體積系數，取值為 1；ρo為油的密度，kg/m3；μo、μw分別為油、水的黏度，mPa·s。

公式(4)變形為

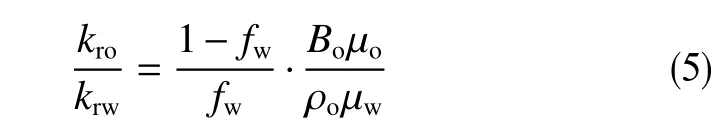
根據文獻［14-15］計算平均含水飽和度與出口端含水飽和度的關系為

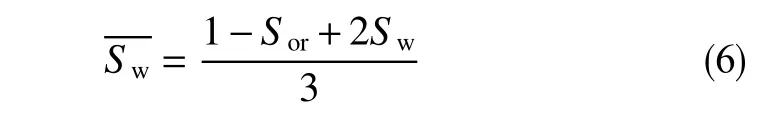
式中，Sw為平均含水飽和度，Sw為出口端含水飽和度。

平均含水飽和度與采出程度的關系式為

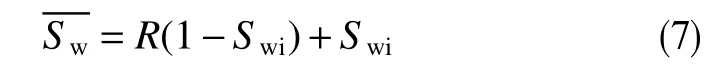
式中，R為油藏采出程度。

將式(7)代入式(6)可得

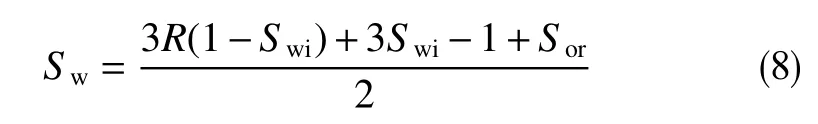
將式(5)、(8)代入式(3)得

可根據油田采出程度R和含水率fw數據應用最小二乘原理對式(9)進行非線性回歸［16-19］，求出co、cw、krw(Sor)、Sor，將co、cw、krw(Sor)、Sor的值代入式(1)、(2)，可計算得出相滲曲線。

1.2 實例應用

江蘇油田高6 斷塊油藏原油體積系數為1.103 5，地下原油黏度為8.41 mPa · s，地層水黏度為0.427 mPa · s，束縛水飽和度為0.348，束縛水飽和度下的油相相對滲透率為0.99。

利用表1 中的數據對式(7)進行回歸，得到參數co=5.001、cw=1.71，krw(Sor)=0.466，Sor=0.177。將co、cw、krw(Sor)、Sor的值代入式 (1)與式 (2)求出相滲曲線。將動態數據反演得到的相滲曲線與巖心實驗得到的常規相滲曲線進行對比，如圖1 所示。

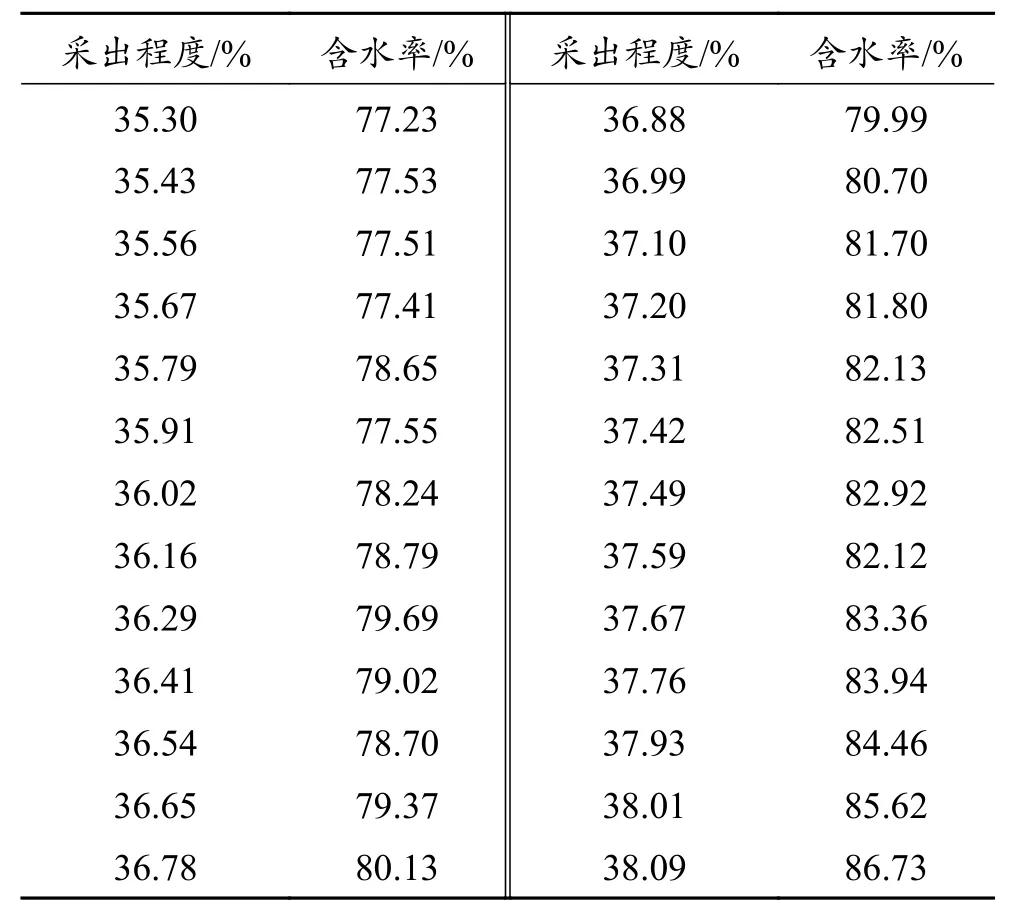
表1 油田生產數據Table 1 Oilfield production data

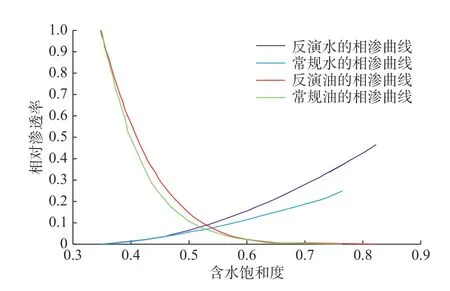
圖1 相對滲透率曲線對比Fig.1 Comparison of relative permeability curves

從圖1 可以看出，常規的相滲曲線和反演所得的相滲曲線左側端點值相同，即常規相滲曲線與基于動態數據反演的相滲曲線的束縛水飽和度相同；常規的相滲曲線的右側端點值小于反演所得的相滲曲線右側端點值，即基于動態數據反演的相滲曲線殘余油飽和度要低于常規相滲曲線的。從整體來看，基于動態數據反演的相滲曲線的相對滲透率要高于常規相滲曲線的，這是注水沖刷所導致的儲層滲透率升高在相滲曲線中的一個表現。常規相滲曲線是由室內實驗測得，注水倍數遠小于真實油藏生產控制條件，具有很大的局限性，而通過動態數據反演可以很好的彌補室內實驗的不足，得到的相滲曲線能更加貼近油藏實際狀況。

2 在數模中的應用效果

江蘇油田高6 斷塊模型的網格劃分為65×186×44，x方向的網格步長為 3.18～53.5 m，y方向的網格步長為 13.76～26.06 m，z方向上的網格步長為0～19.79 m。模型的平均孔隙度為16.97%，平均滲透率為 70.36×10-3μm2，初始含油飽和度如圖2 所示。

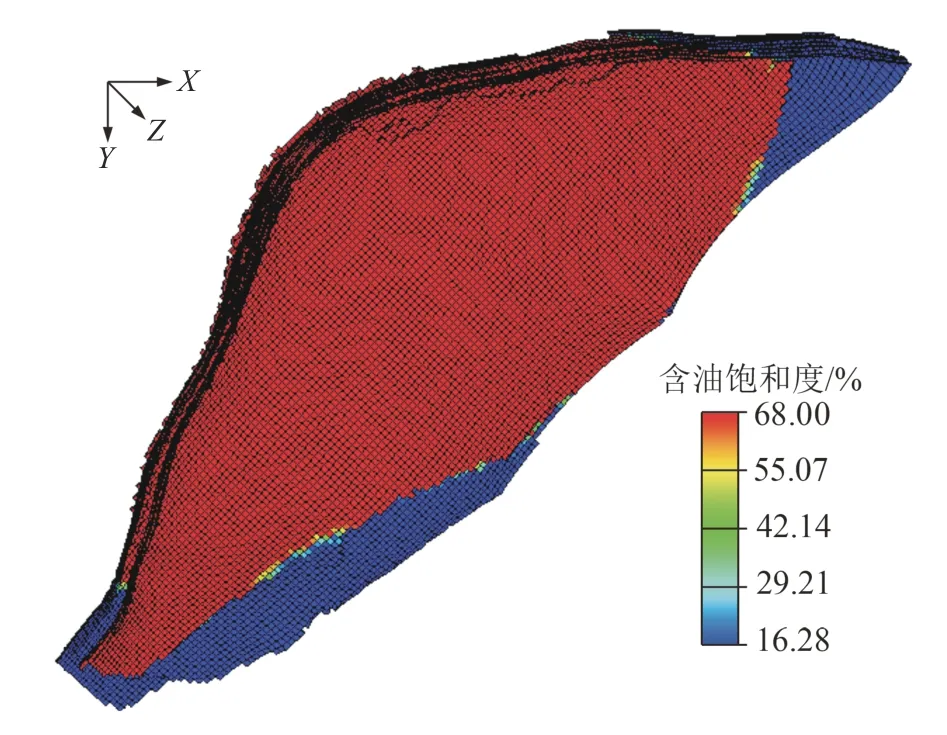
圖2 初始含油飽和度Fig.2 Initial oil saturation

在高6 斷塊中分別使用動態數據反演得到的相滲曲線與巖心驅替實驗所得的常規相滲曲線進行數值模擬，研究動態數據反演得到的相滲曲線表征油水流動能力的準確性。由圖3 可以看出，基于動態數據反演的相滲曲線所獲得的含水率變化規律更加貼近實際生產變化規律。這是因為地層經長期注水沖刷后，儲層物性發生變化，而基于動態數據反演的相滲曲線可以體現該變化，更加準確地表征油水的實際流動能力，在數值模擬中具有較好的應用效果。

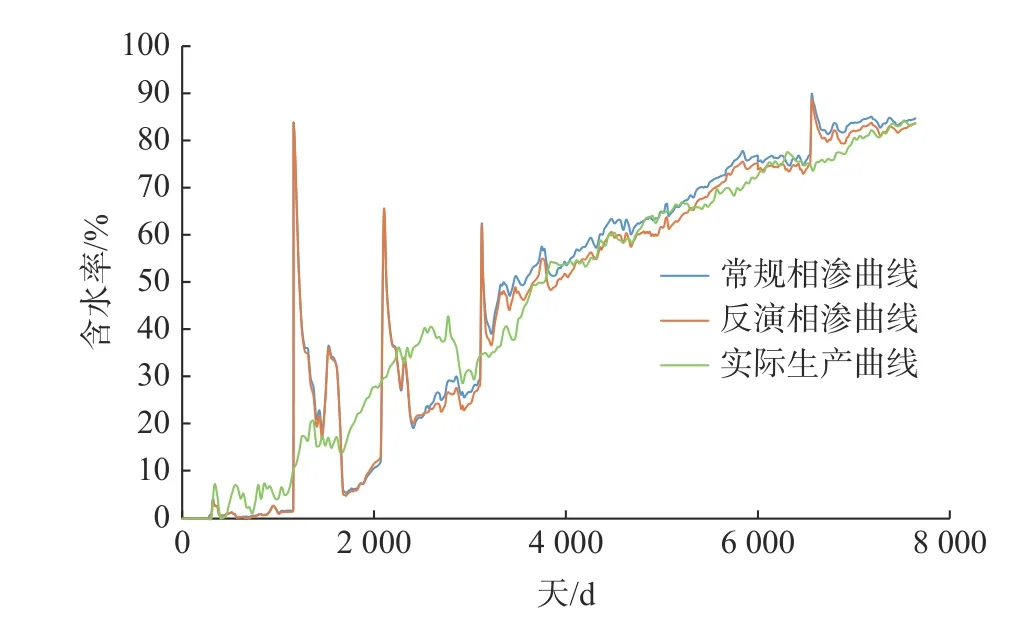
圖3 含水率對比Fig.3 Comparison of water cut

3 動態數據反演得到的相滲曲線對剩余油分布的影響

用Eclipse 的黑油模型進行模擬，建立機理模型，模型網格劃分為 21×1×5，x方向網格步長均為20 m，y方向網格步長均為10 m，z方向網格步長約為2 m。模型孔隙度為16.97%，模型的滲透率從上往下依次升高，滲透率分布如圖4 所示(模型局部放大圖)。

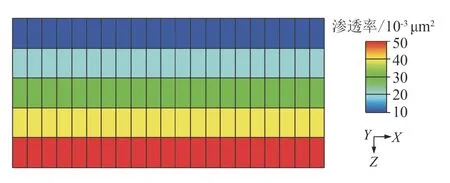
圖4 滲透率分布Fig.4 Permeability distribution

分別使用基于動態數據反演的相滲曲線與巖心驅替實驗所得的常規相滲曲線進行模擬，在達到特高含水期后，對比油藏的開發效果。如圖5 所示，與應用常規相滲曲線所得的結果相比，基于動態數據反演的相滲曲線下，剩余油飽和度高的區域變得更高，剩余油飽和度低的區域變得更低。統計油層頂部與底部含油飽和度的比值，常規相滲對應的比值為1.25，動態數據反演得到的相滲對應的比值為1.43，可以看出，儲層的動態非均質性更加嚴重。

4 結論

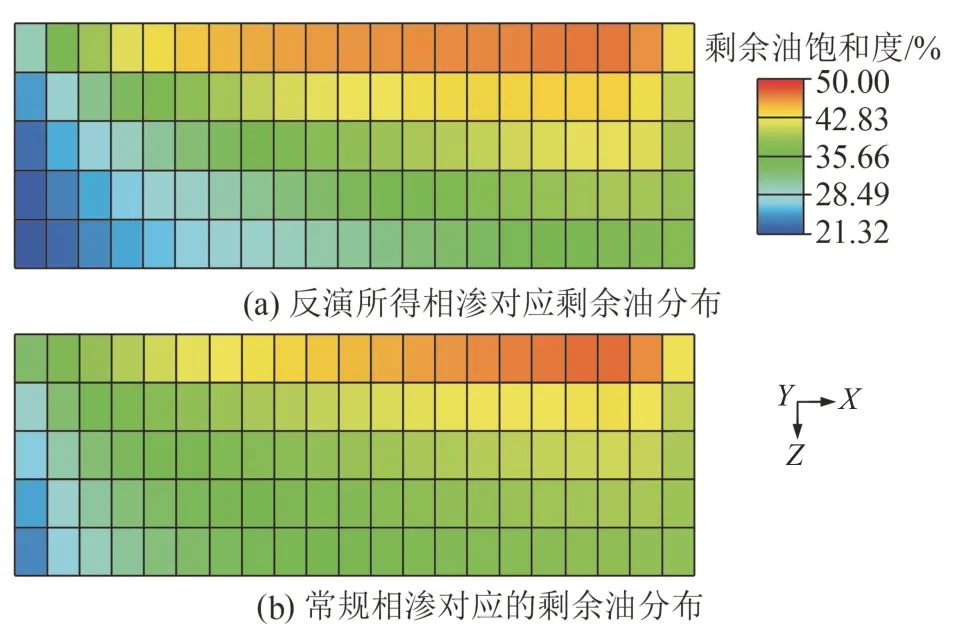
圖5 剩余油分布對比Fig.5 The comparison of remaining oil distribution

(1)利用綜合反映油藏儲層物性、開發方式等變化的動態生產數據，反演獲得了真實反映油水流動能力的相對滲透率曲線。在實際油藏中，通過對比含水率的變化，發現與基于常規巖心實驗獲得的滲透率模擬結果相比，基于動態數據反演的相對滲透率曲線更貼近實際含水率的變化規律，驗證了反演滲透率的準確性。

(2)采用數值模擬對比分析了相對滲透率曲線對剩余油分布的影響，發現與常規巖心驅替實驗獲得的相滲曲線相比，基于動態數據反演的相滲曲線下，剩余油飽和度高的區域變得更高，剩余油飽和度低的區域變得更低，剩余油分布的非均質性加劇。