33 t 軸重重載鐵路軌道結構合理剛度研究

朱利軍，劉永孝

（ 蘭州交通大學 土木工程學院，蘭州 730070 ）

重載鐵路以其運能大、效率高、運輸成本低而受到世界各國運輸部門的重視，并得以迅速發展，已成為世界鐵路發展的重要趨勢[1]。在國外，美國鐵路線路的70% 是重載鐵路，列車標準軸重為33 t，最大允許軸重可達35.7 t。澳大利亞更是在上世紀末將軸重提升至37.5 t，刷新了重載鐵路的世界紀錄。國內重載鐵路也在加快發展，2006 年大秦鐵路正式開行2 萬t 重載組合列車，列車軸重25 t。而由國內運輸需求大數據分析可知，為促進經濟發展，需大力發展重載鐵路，提高運輸軸重，優化軌道結構。這也是我國鐵路以建設創新鐵路為目標，以增強自主創新能力為核心的一項重要舉措[2-3]。

國內外對軌道結構的研究眾多，研究方法包括模擬動態荷載和車輛軌道耦合動力學等[4-6]。目前，軌道剛度研究方法主要有準靜態法和敏感系數法。文獻[7]和文獻[8]中分別運用準靜態法分析了大軸重貨車作用下的有砟和無砟軌道結構；文獻[9]中運用ANSYS 建模，采用動力學方法分析了大軸重貨車作用下有砟軌道結構的動力響應。綜上，國內學者提出了敏感系數法并分析了高速鐵路無砟軌道結構與客貨共線鐵路無砟軌道結構；本文以敏感系數和目標函數為分析方法研究重載鐵路有砟軌道結構，考慮動荷載對鋼軌、軌枕和道床動力響應的影響，運用動力學，科學地評價軌道結構動力響應，得出軌道結構部件剛度的優化值。

1 軌道剛度準靜態計算

對有砟軌道結構剛度組成進行分析，軌道整體剛度可視為由各個部件剛度由上而下串聯而成。國內鋼軌和軌枕皆按照標準進行生產，其剛度基本恒定，因此，扣件- 墊板剛度和道床剛度便成了決定軌道結構剛度的重要因素。軌道剛度的準靜態計算方法有允許應力法和允許變形法，本文分別依照這兩種方法進行33 t 軸重貨車作用下軌道剛度計算。計算中，靜態輪軌力F0=165 kN ；參照《重載鐵路設計規范》，動載系數取定為2.5，則準靜態垂向荷載F=2.5F0；軌枕間距a=600 mm ；鋼軌類型為75 軌。

1.1 允許應力法

根據Winkler 假設，將鋼軌視為連續彈性基礎上的無限長梁，可得：

其中，ku=kD/a，k為軌道的整體剛度，y為鋼軌的豎向位移，M0為鋼軌跨中的彎矩，W下為鋼軌底部的抗彎模量，EI為鋼軌的垂向抗彎剛度，ku為鋼軌的基礎彈性模量，kD為鋼軌支點剛度，σGmax為軌底的最大應力，PZmax為軌枕上的最大壓力，q0為軌枕上的線荷載集度。

由公式（1） ～（3） 可知， 鋼軌應力和枕上壓力共同控制軌下基礎剛度的取值，即要滿足：σGmax≤[σG]且PZmax≤[σZ]，其中，[σG]為軌底允許拉應力，由美國鐵路工程協會推薦的公式計算得[σG]=145 MPa，[σZ]為枕上允許壓力，根據重載軌枕設計要求，枕上允許壓力[σZ]=185 kN。

1.2 允許變形法

對于軌道結構而言，鋼軌直接承受列車荷載，并將荷載分配向下傳遞。在此過程中，鋼軌會因承受荷載而產生垂向變形，而鋼軌的變形必須在一定的限值之內，否則會對軌道結構的平順性產生影響，從而影響行車安全。

綜上可知， 鋼軌基礎彈性模量取值應為140.99 N/mm2～184.75 N/mm2， 由ku和kD的 關系可知，鋼軌支點剛度控制范圍為84.59 kN/mm ～110.85 kN/mm。考慮到扣件彈性墊層的動靜剛度比為1.0 ～1.2，以及彈性墊層的生產誤差，軌下扣件- 墊板的剛度取值為100 kN/mm ～200 kN/mm。

由以上計算可以得出軌下墊板的合理剛度取值范圍，但無法準確得出33 t 軸重貨車作用下軌道機構的合理剛度。因此，為確定軌道結構剛度的最優組合，需采用動力學方法進行分析，實現軌道結構的最優匹配。

2 車輛-軌道耦合動力學仿真

本文參考文獻[5]和文獻[6]，建立貨車- 軌道垂向動力學模型，貨車- 軌道耦合動力學方程為：

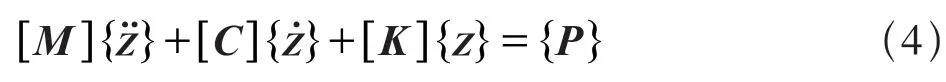
其中，[M]、[C]、[K]、{P} 分別為振動系統的總質量矩陣、總阻尼矩陣、總剛度矩陣及荷載列陣；分別為振動系統的加速度、速度及位移列陣。動力仿真計算使用Matlab 編程完成計算，使用newmark 法進行數值積分。

2.1 車輛模型

對車輛建模時，貨車被模擬為一個以速度v運行于軌道結構上的多剛體系統，參考C80 貨車建立模型。模型中，考慮車體及轉向架的浮沉和點頭運動，以及4 個輪對的垂向運動，共計10 個自由度。

車輛模型參數包括：車體、轉向架和輪對質量，分別為124 t、1.25 t 和1.277 t ；車體和轉向架點頭轉動慣量分別為142 800 kg?m2和318 kg?m2；車輛定距及固定軸距為8.2 m 和1.83 m ；一系、二系懸掛剛度為60 MN/m 和6 MN/m ；一系、二系懸掛阻尼為4 kNs/m 和50 kNs/m。

2.2 軌道動力學模型

如圖1 所示，軌道結構簡化為鋼軌、軌枕和道床3 層結構；自上而下，將鋼軌視為平面梁單元，以扣件支撐處為節點，進行單元劃分；每一軌枕視為一個單節點單元；參照軌枕，將道床也劃分為單節點單元。因此，軌道結構須考慮鋼軌的垂向位移、彎曲自由度以及軌枕和道床的垂向自由度。將鋼軌與軌枕、軌枕與道床、道床與路基之間的連接均視為彈簧阻尼系統間的連接。考慮到軌道模型長度過長會影響計算效率，設置軌道模型長度為199 個跨距。鋼軌采用標準75 軌，軌枕采用混凝土Ⅲ型軌枕。

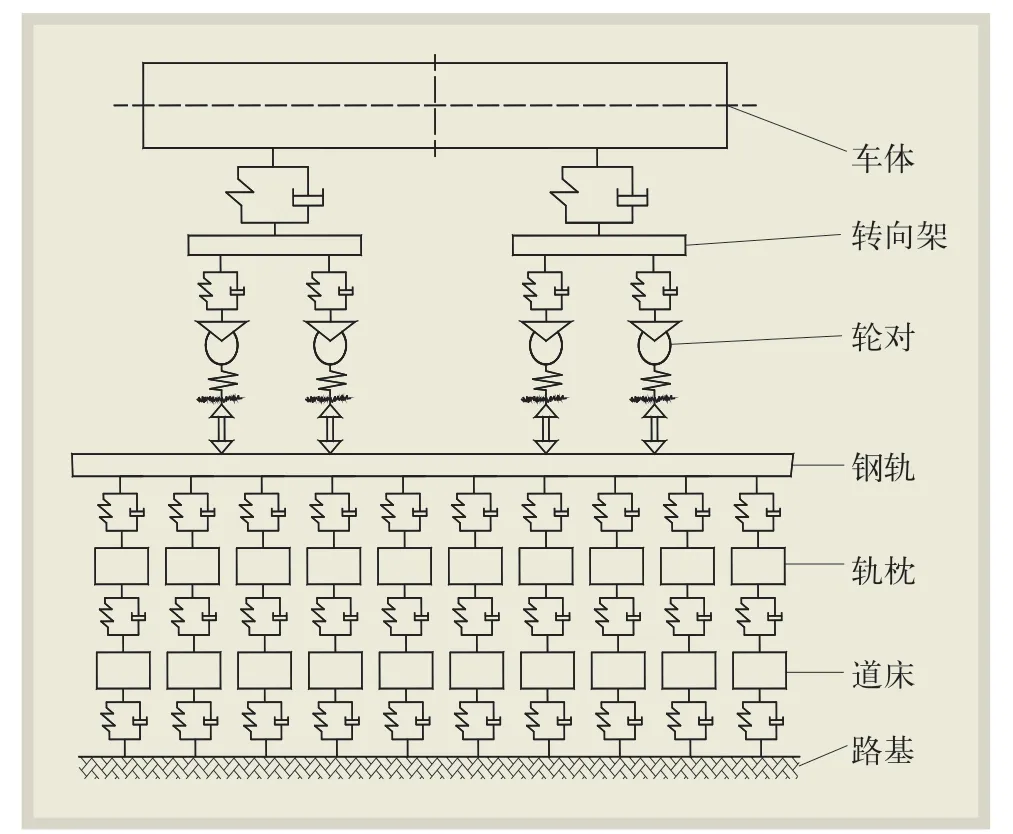
圖1 貨車- 軌道垂向耦合動力學模型示意圖

2.3 接觸模型

將輪軌的垂向接觸簡化為彈簧接觸，接觸力的大小通過輪軌間的接觸點變形大小來求解，輪軌力計算公式為：

從式(12)可知球形譯碼更新半徑中的未知項服從自由度為k的非中心卡方分布，由于期望值反映的是隨機變量輸出值的平均數，因此很容易想到使用期望來估計式(13)中的未知項.非中心卡方分布的期望計算如下：

其中，δZ(t) 為輪軌間的彈性壓縮量；G為輪軌接觸常數(m/N2/3)。

建模所用的C80 貨車采用磨耗型踏面， 即G=3.86R-0.115×10-8，其中，R為車輪半徑。

2.4 軌道不平順

依據大秦鐵路實際運營條件，本文軌道不平順選擇與我國重載鐵路情況比較相似的美國五級譜，將其做為輸入激勵，波長為1.5 m ～250 m，不平順樣本如圖2 所示。

圖2 美國五級譜軌道不平順樣本圖

3 軌道結構合理剛度的研究

目前，在我國既有重載鐵路軌道結構上，彈條Ⅱ型扣件和Ⅲ型混凝土軌枕的使用最為廣泛，由此確定扣件系統的垂向剛度優化范圍為：40 kN/mm ～180 kN/mm ；依據鐵路軌道設計規范內容以及驗收標準規定，普速鐵路Ⅲ型軌枕支承剛度不小于100 kN/mm，則軌枕支點下道床剛度的仿真模擬優化范圍取100 kN/mm ～275 kN/mm ；依照重載鐵路設計規范，再參考大秦鐵路和浩吉鐵路，仿真行車速度取80 km/h。

3.1 軌道結構剛度對系統動力特性的影響

圖3 ～圖6 中分別給出了不同軌道部件剛度條件下軌道結構動力的相應變化（部分圖中僅繪出4 種道床條件下的變化）。由圖可知：（1）輪軌垂向力、枕上壓力均隨著扣件剛度、道床剛度的增加而增加；（2）鋼軌垂向位移隨扣件剛度和道床剛度的增大而減小，軌枕垂向位移隨扣件剛度增大而增大，隨道床剛度增大而減小，道床垂向位移隨扣件剛度和道床剛度的增大而增大；（3）鋼軌加速度變化較為復雜，扣件剛度小于100 kN/mm 時，與扣件剛度成反比，與道床剛度成正比；扣件剛度大于100 kN/mm 時，與扣件剛度成正比，與道床剛度成反比；（4）軌枕、道床加速度均隨部件剛度增大而增大。

圖3 軌道結構動力響應圖1

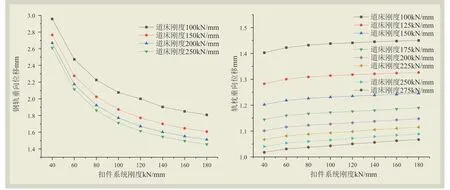
圖4 軌道結構動力響應圖2

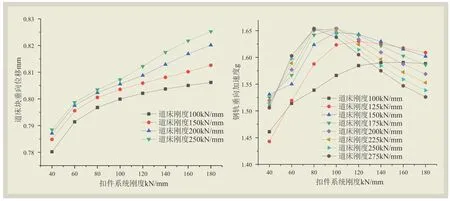
圖5 軌道結構動力響應圖3

圖6 軌道結構動力響應圖4

3.2 軌道結構最優匹配剛度

本文采用敏感系數法定量描述軌道動力參數對部件剛度變化的響應。將動力參數變化率與剛度比值變化率之比定義為參數的敏感系數ξD，即部件剛度由k1變化至k2，由此引起的某一動力參數D從D1變化至D2，計算公式為：

按公式（6）分別計算上述動力參數在扣件剛度、道床剛度變化區間內的敏感系數，由于單個動力參數對單個剛度變化的敏感系數變化不大，取敏感系數的平均值進行分析，結果如表1 所示。

表1 敏感系數列表

其中，ξ1表示各個動力參數對扣件剛度變化的敏感系數；ξ2表示各個動力參數對道床剛度變化的敏感系數。由表1 可知，鋼軌位移對扣件剛度最為敏感，其次是軌枕加速度和道床加速度，輪軌力和鋼軌加速度對扣件剛度變化的敏感度最低；軌枕位移對道床剛度變化最為敏感，其次是鋼軌位移及道床加速度，輪軌力和鋼軌加速度對道床剛度變化的敏感度最低。

綜上，各個動力參數對部件剛度的敏感系數各不相同，當部件剛度改變時，主要動力參數的變化比較復雜，綜合考慮軌道結構復雜響應變化，以其動力特性變化最小為目標建立目標函數，公式為：

其中，ξ1D1、ξ1D2、…、ξ1D8分別代表了輪軌垂向力、枕上壓力、鋼軌位移、軌枕位移、道床位移、鋼軌加速度、軌枕加速度和道床加速度對扣件剛度變化的敏感系數；ξ2D1、ξ2D2、…、ξ2D8為各個動力參數對道床剛度變化的敏感系數；Fr、Fb、ur、ub、us、ar、ab、as分別為輪軌垂向力、枕上壓力、鋼軌位移、軌枕位移、道床位移、鋼軌加速度、軌枕加速度和道床加速度；Fbr、Fbb、ubr、ubb、ubs、abr、abb、abs分別為軌道結構相應的標準參數[10-11]。將仿真計算結果帶入目標函數，計算不同軌道結構部件剛度組合下的目標函數值，計算結果如表2 所示，當扣件剛度為120 kN/mm，道床剛度為175 kN/mm 時，目標函數取得最小值0.021。因此，由敏感系數法得到的軌道結構的最優剛度匹配為：扣件系統剛度為120 kN/mm，道床剛度為175 kN/mm。

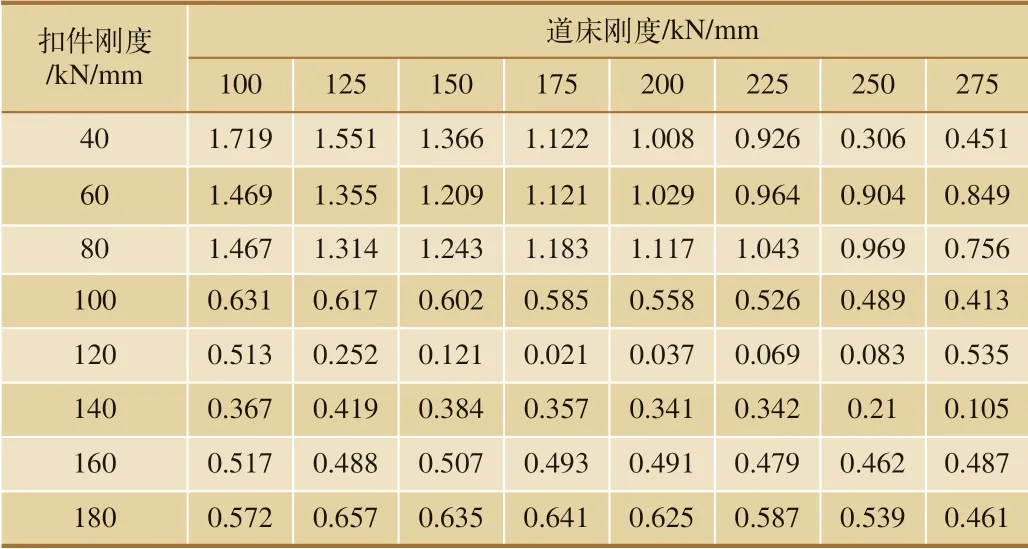
表2 目標函數值列表

4 結束語

本文基于連續彈性地基梁模型并結合我國既有重載線路的實際應用經驗，對重載鋼軌軌道剛度進行準靜態計算，編程進行動力仿真，引入敏感系數，分析選定參數對軌道結構剛度的響應，依據軌道剛度合理取值的優化目標函數，找出軌道部件剛度合理匹配軌道整體剛度的取值，結論如下：

（1）由準靜態法得出的33 t 軸重重載鐵路有砟軌道扣件剛度最優取值范圍為100 kN/mm ～200 kN/mm。

（2）引入敏感系數，建立目標函數計算得出33 t 軸重有砟軌道結構最優剛度匹配為：扣件剛度為120 kN/mm，道床剛度為175 kN/mm。

本文提出的扣件彈性墊層剛度及道床剛度取值，還有待于在實踐中進一步完善，以發揮其最大的經濟效益。